第8章:树
1.树是什么
- 一种
分层数据的抽象模型 - 前端工作中常见的树包括:DOM树,级联选择(省市区),树形控件,…
- javascript中没有树,但是可以用Object和Array构建树

4.树的常用操作:深度/广度优先遍历,先中后序遍历
深度 / 广度遍历
深度优先遍历:尽可能深的搜索树的分支。如下图深度访问顺序:
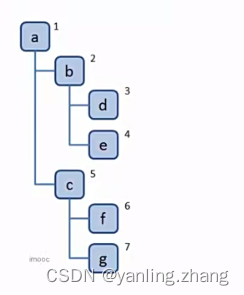
广度优先遍历:先访问离跟节点最近的节点。
标题,目录,深入看每个目录下的小节。
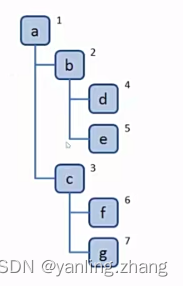
深度优先遍历算法口诀:(其实就是一个递归)
1.访问根节点。
2.对根节点的children挨个进行深度优先遍历。

只有2步,写代码也只有2行代码,但是这2行代码实现了深度优先递归,在遍历的过程中被反复调用很多次。
const tree = {val: 'a',children: [{val: 'b',children: [{val: 'd',children: []},{val: 'e',children: []}]},{val: 'c',children: [{val: 'f',children: []},{val: 'g',children: []}]}]
}
const dfs = function (tree) {console.log(tree.val)// root.children.forEach((child) => dfs(child))root.children.forEach(dfs)
}
广度优先遍历算法口诀(对列)
1.新建一个队列,把根节点入队
2.把队头出队并访问
3.把队头的children挨个入队
4.重复第2,3步,知道队列为空。

const root = {val: 'a',children: [{val: 'b',children: [{val: 'd',children: []},{val: 'e',children: []}]},{val: 'c',children: [{val: 'f',children: []},{val: 'g',children: []}]}]
}const bfs = function (root) {const q = [root]while(q.length > 0) {const n = q.shift()console.log(n.val)if (n.children) {n.children.forEach(child => {q.push(child)})}}
}二叉树的先,中, 后序的三种遍历
1.二叉树:树中每个树的节点最多有2个节点
2.在js中通常用Object来模拟二叉树

先序遍历:(根,左,右)
1.访问根节点
2.对结节点的左子树进行先序遍历
3.对根节点的右子树进行先序遍历

如上图:访问顺序:1,2, 4, 5,3, 6, 7
const bt = {val: 1,left: {val: 2,left: {val: 4,left: {},right: {}},right: {val: 5,left: {},right: {}}},right: {val: 3,left: {val: 6,left: {},right: {}},right: {val: 7,left: {},right: {}}}}const preorder = function (root) {if (!root) return // 访问根节点console.log(root.val)preorder(root.left)preorder(root.right)
}
中序遍历
相关文章:

第8章:树
1.树是什么 一种分层数据的抽象模型前端工作中常见的树包括:DOM树,级联选择(省市区),树形控件,…javascript中没有树,但是可以用Object和Array构建树 4.树的常用操作:深度/广度优先遍历,先中后…...

Java基础学习(10)
Java基础学习 一、JDK8时间类1.1 Zoneld时区1.2 Instant时间戳1.3 ZonedDateTime1.4 DateTimeFormatter1.5 日历类时间表示1.6 工具类1.7 包装类JDK5提出的新特性Integer成员方法 二、集合进阶2.1 集合的体系结构2.1.1 Collection 2.2collection的遍历方式2.2.1 迭代器遍历2.2.…...
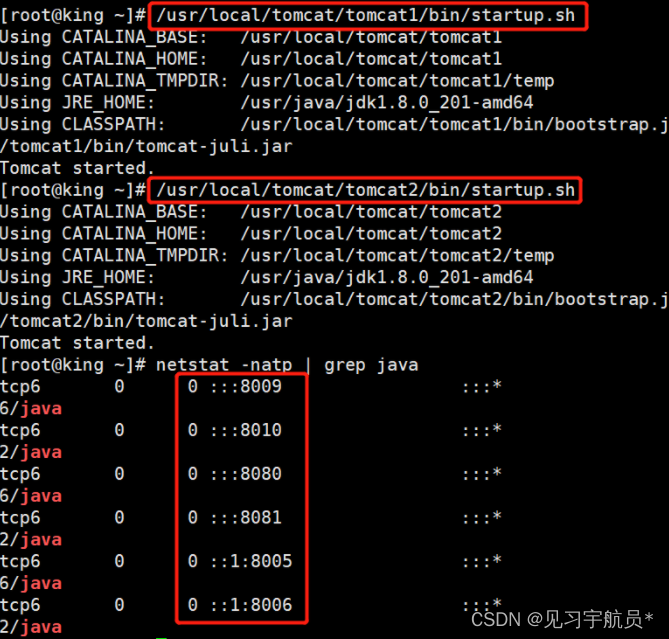
Tomcat多实例部署实验
引言 本文主要内容是tomcat的多实例配置实验。 一、实验准备 Tomcat多实例是指在一台设备上运行多个Tomcat服务,这些Tomcat相互独立,互不影响。多实例与虚拟主机不同,虚拟主机的本质是在一个服务下有多个相对独立的目录,但是多实…...

无良公司把我从上家挖过来,白嫖了六个月,临近试用期结束才说不合适,催我赶紧找下家!...
职场套路多,一不小心就会掉坑,一位网友讲述了自己的遭遇: 今天被领导催促离职了,当时就是这个领导把他从别的公司挖过来。这家公司催得太急,为了投奔这里,他和上家的HR都闹翻了,上家总监挽留他&…...

忙碌中也要记得休息,这两款好玩的游戏推荐给你
第一款:古墓丽影9年度版 《古墓丽影9》(原名Tomb Raider)是由水晶动力开发,史克威尔艾尼克斯发行的动作冒险游戏。 它于 2013 年发布。续集是古墓丽影崛起和古墓丽影暗影。 本作的重点是新版劳拉(Lara Croft…...

四种方法可以实现判断字符串包含某个字符
小编介绍过js中使用indexOf() 方法判断字符串包含某个字是一个很好用的方法,但除了这个方法之外,JavaScript中还有四种方法可以实现判断字符串包含某个字符: 1、使用字符串search() 方法 search() 方法用于检索字符串中指定的子字符串&…...

ubuntu进程相关command
列出当前系统中所有正在运行的进程的详细信息 ps aux查看所有包含某关键字的进程 例:查看所有包含关键字click的进程 ps aux | grep click运行后显示如下信息: root 8998 0.0 0.0 10984 4052 ? S 4月23 0:00 sudo ./bin/click…...

7.参数校验
在controller和service进行前端传参校验,保证存到数据库的数据是正确的 1.引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-validation</artifactId></dependency>这里无需…...
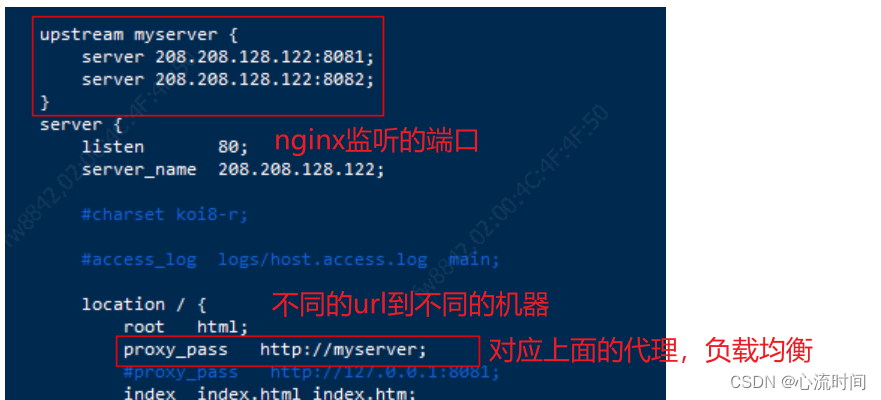
nginx简单介绍
文章目录 1. 下载并解压2. 80端口被占用,更改nginx默认的监听端口3. 访问nginx4. 在linux上安装nginx5. nginx常用命令6. nginx.conf 1. 下载并解压 官网下载 2. 80端口被占用,更改nginx默认的监听端口 更改conf/nginx.conf文件 3. 访问nginx ht…...

美创科技首届渠道高峰论坛| 两大分论坛亮点汇聚
4月22日,美创科技首届渠道高峰论坛在海南三亚隆重举行,本届高峰论坛以“新起点 新战略 共赢数安蓝海”为主题,全国各地200余家合作伙伴齐聚。当日下午,行业分论坛、技术分论坛两大论坛以及圆桌会议,多方视角、全方位共…...

QML中【预计符号】和【Unknown Component M300】的红色警告解决方法
问题描述: QML的项目中带中文,每次打开项目都在问题栏显示【预计符号】的红色警告,还有一种是【Unknown Component M300】的警告,代码能正常编译和运行。像我这样对代码追求优雅的强迫症患者看着很不爽,查了很多网上的…...
聊聊「低代码」的实践之路
区块链、低代码、元宇宙、AI智能; 01 【先来说说背景】 这个概念由来已久,但是在国内兴起,是最近几年; 低代码即「Low-Code」; 指提供可视化开发环境,可以用来创建和管理软件应用; 简单的说…...

(一)服务发现组件 Eureka
1、Eureka 简介 Eureka 是Spring Cloud Netflix 微服务套件中的一部分, 它基于Netflix Eureka 做了二次封装, 主要负责完成微服务架构中的服务治理功能。我们只需通过简单引入依赖和注解配置就能让Spring Boot 构建的微服务应用轻松地与Eureka 服务治理…...
学会笔记本电脑录屏快捷键,轻松实现录屏!
案例:笔记本电脑录屏有快捷键吗? 【我每次打开笔记本电脑录屏都要耗费比较长的时间,这样会影响到我录屏的效率。在这里想问一下,有没有快速打开电脑录屏的方法?】 在日常的工作、学习、娱乐中,我们经常需…...

( “树” 之 Trie) 208. 实现 Trie (前缀树) ——【Leetcode每日一题】
知识点回顾 : Trie,又称前缀树或字典树,用于判断字符串是否存在或者是否具有某种字符串前缀。 ❓208. 实现 Trie (前缀树) 难度:中等 Trie(发音类似 “try”)或者说 前缀树 是一种树形数据结构ÿ…...
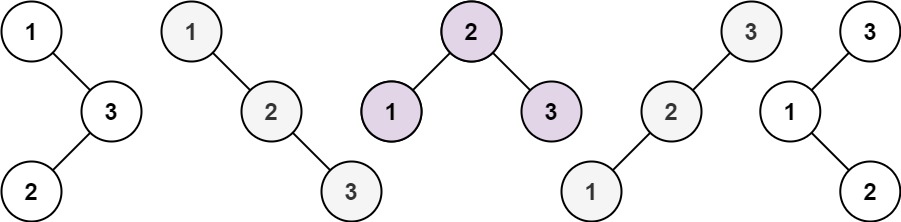
算法训练Day40:343. 整数拆分 96.不同的二叉搜索树
文章目录 整数拆分题解(动态规划)贪心 不同的二叉搜索树题解 整数拆分 CategoryDifficultyLikesDislikesContestSlugProblemIndexScorealgorithmsMedium (62.22%)11660--0 Tags 数学 | 动态规划 Companies 给定一个正整数 n ,将其拆分为…...

设计模式及代码
1、工厂方法模式(Factory Method Pattern): 定义一个用于创建对象的接口,让子类决定实例化哪一个类。应用场景:当一个类不知道它所必须创建的对象的类时;一个类希望由它的子类来指定它所创建的对象时。 抽…...
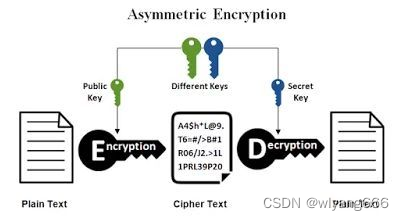
9.java程序员必知必会类库之加密库
前言 密码学在计算机领域源远流长,应用广泛。当前每时每刻,每一个连接到互联网的终端,手机,电脑,iPad都会和互联网有无数次的数据交互,如果这些数据都是明文传输那将是难以想象的。为了保护用户隐私&#…...

C技能树:for循环:九九乘法表
使用for循环,打印九九乘法表。下列四个选项中有一项无法实现该功能,请找出该错误选项。 #include <stdio.h> int main(int argc, char** argv) {int i 0;int j 0;(_____1_____)return 0; } int row 0; int col 0; for(i 0; i < 8…...

Win10老是蓝屏收集错误信息重启无效怎么办?
Win10老是蓝屏收集错误信息重启无效怎么办?有用户遇到了电脑开机蓝屏的情况,收集错误信息重启电脑之后,依然无法解决问题。那么这个问题要怎么去进行解决呢?接下来我们来看看以下具体的处理方法教学吧。 准备工作: 1、…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

shell脚本质数判断
shell脚本质数判断 shell输入一个正整数,判断是否为质数(素数)shell求1-100内的质数shell求给定数组输出其中的质数 shell输入一个正整数,判断是否为质数(素数) 思路: 1:1 2:1 2 3:1 2 3 4:1 2 3 4 5:1 2 3 4 5-------> 3:2 4:2 3 5:2 3…...

基于 HTTP 的单向流式通信协议SSE详解
SSE(Server-Sent Events)详解 🧠 什么是 SSE? SSE(Server-Sent Events) 是 HTML5 标准中定义的一种通信机制,它允许服务器主动将事件推送给客户端(浏览器)。与传统的 H…...

CentOS 7.9安装Nginx1.24.0时报 checking for LuaJIT 2.x ... not found
Nginx1.24编译时,报LuaJIT2.x错误, configuring additional modules adding module in /www/server/nginx/src/ngx_devel_kit ngx_devel_kit was configured adding module in /www/server/nginx/src/lua_nginx_module checking for LuaJIT 2.x ... not…...
