算法训练Day40:343. 整数拆分 96.不同的二叉搜索树
文章目录
- 整数拆分
- 题解(动态规划)
- 贪心
- 不同的二叉搜索树
- 题解
整数拆分
| Category | Difficulty | Likes | Dislikes | ContestSlug | ProblemIndex | Score |
|---|---|---|---|---|---|---|
| algorithms | Medium (62.22%) | 1166 | 0 | - | - | 0 |
数学 | 动态规划
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
提示:
2 <= n <= 58
Discussion | Solution
题解(动态规划)
// @lc code=start
class Solution {
public:int integerBreak(int n) {vector<int> dp(n+1);dp[2] = 1;for(int i = 3; i <= n; ++i) {for(int j = 1; j <= i/2; ++j) {dp[i] = max(dp[i],max((i-j) * j,dp[i-j]*j));}}return dp[n];}
};
- 时间复杂度:O(n^2)
- 空间复杂度:O(n)
贪心
本题也可以用贪心,每次拆成n个3,如果剩下是4,则保留4,然后相乘,但是这个结论需要数学证明其合理性!
我没有证明,而是直接用了结论。感兴趣的同学可以自己再去研究研究数学证明哈。
给出我的C++代码如下:
class Solution {
public:int integerBreak(int n) {if (n == 2) return 1;if (n == 3) return 2;if (n == 4) return 4;int result = 1;while (n > 4) {result *= 3;n -= 3;}result *= n;return result;}
};
- 时间复杂度:O(n)
- 空间复杂度:O(1)
不同的二叉搜索树
| Category | Difficulty | Likes | Dislikes | ContestSlug | ProblemIndex | Score |
|---|---|---|---|---|---|---|
| algorithms | Medium (70.86%) | 2213 | 0 | - | - | 0 |
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
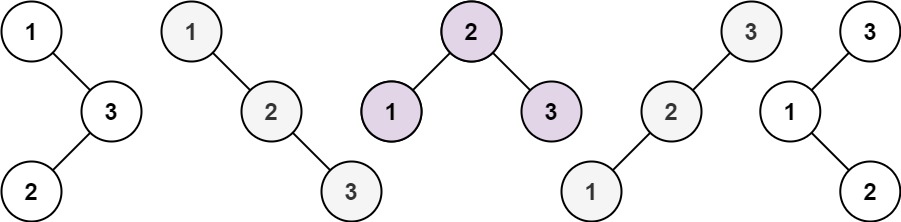
输入:n = 3
输出:5
示例 2:
输入:n = 1
输出:1
提示:
1 <= n <= 19
Discussion | Solution
题解
// @lc code=start
class Solution {
public:int numTrees(int n) {vector<int> dp(n+1);dp[0] = 1;for(int i = 1;i <=n; ++i) {for(int j = 1; j <= i;++j) {dp[i] += dp[j-1] * dp[i-j]; }}return dp[n];}
};
for(int j = 1; j <= i;++j) {dp[i] += dp[j-1] * dp[i-j]; }}return dp[n];
}
};
参考文章:[代码随想录 (programmercarl.com)](https://programmercarl.com/0096.不同的二叉搜索树.html#思路)
相关文章:

算法训练Day40:343. 整数拆分 96.不同的二叉搜索树
文章目录 整数拆分题解(动态规划)贪心 不同的二叉搜索树题解 整数拆分 CategoryDifficultyLikesDislikesContestSlugProblemIndexScorealgorithmsMedium (62.22%)11660--0 Tags 数学 | 动态规划 Companies 给定一个正整数 n ,将其拆分为…...

设计模式及代码
1、工厂方法模式(Factory Method Pattern): 定义一个用于创建对象的接口,让子类决定实例化哪一个类。应用场景:当一个类不知道它所必须创建的对象的类时;一个类希望由它的子类来指定它所创建的对象时。 抽…...
9.java程序员必知必会类库之加密库
前言 密码学在计算机领域源远流长,应用广泛。当前每时每刻,每一个连接到互联网的终端,手机,电脑,iPad都会和互联网有无数次的数据交互,如果这些数据都是明文传输那将是难以想象的。为了保护用户隐私&#…...

C技能树:for循环:九九乘法表
使用for循环,打印九九乘法表。下列四个选项中有一项无法实现该功能,请找出该错误选项。 #include <stdio.h> int main(int argc, char** argv) {int i 0;int j 0;(_____1_____)return 0; } int row 0; int col 0; for(i 0; i < 8…...

Win10老是蓝屏收集错误信息重启无效怎么办?
Win10老是蓝屏收集错误信息重启无效怎么办?有用户遇到了电脑开机蓝屏的情况,收集错误信息重启电脑之后,依然无法解决问题。那么这个问题要怎么去进行解决呢?接下来我们来看看以下具体的处理方法教学吧。 准备工作: 1、…...

Redis入门学习笔记【五】Redis在分布式环境下常见的应用场景
一、分布式锁 当多个进程不在同一个系统中,用分布式锁控制多个进程对资源的操作或者访问。 与之对应有线 程锁,进程锁。 分布式锁可以避免不同进程重复相同的工作,减少资源浪费。 同时分布式锁可以避免破坏数据正 确性的发生, …...

Python ZIpFile 解惑:GBK 编码与乱码现象
文章目录 参考描述铺垫乱码现象编码与解码编码解码 字符集Unicode 字符集UTF-8CP437Zip 文件与 CP437 编码 GB2312GB2012GBK 单字节编码与多字节编码 溯源通用标志位与语言编码标志ZipFile 所支持的两种编码方式GBK 编码与 Zip 应用乱码现象产生的原因 解决 参考 项目描述维基…...

【LeetCode】213. 打家劫舍 II
213. 打家劫舍 II(中等) 思路 这道题是 198.打家劫舍 的拓展版,区别在于:本题的房间是环形排列,而198.题中的房间是单排排列。 将房间环形排列,意味着第一间房间和最后一间房间不能同时盗窃,因…...
从初识RabbitMQ到安装了解
一、同步和异步通讯 微服务间通讯有同步和异步两种方式: 同步通讯:就像打电话,需要实时响应。 异步通讯:就像发邮件,不需要马上回复。 两种方式各有优劣,打电话可以立即得到响应,但是你却不…...
-字符串函数的使用解析)
MySQL(六)-字符串函数的使用解析
字符串函数的使用解析 1 计算字符串字符数的函数和字符串长的函数2 合并字符串函数 CONCAT(s1,s2,...)、CONCAT_WS(xs1,s2,...)3 替换字符串函数INSERT(s1,x,len,s2)4 字母大小写转换函数5 获取指定长度的字符串的函数LEFT(s,n)和RIGHT(s,n)6 填充字符串的函数 LPAD(s1,len,s2)…...

Zookeeper集群搭建
搭建Zookeeper集群 1.1 搭建要求 真实的集群是需要部署在不同的服务器上的,但是在我们测试时同时启动很多个虚拟机内存会吃不消,所以我们通常会搭建伪集群,也就是把所有的服务都搭建在一台虚拟机上,用端口进行区分。 我们这里要…...
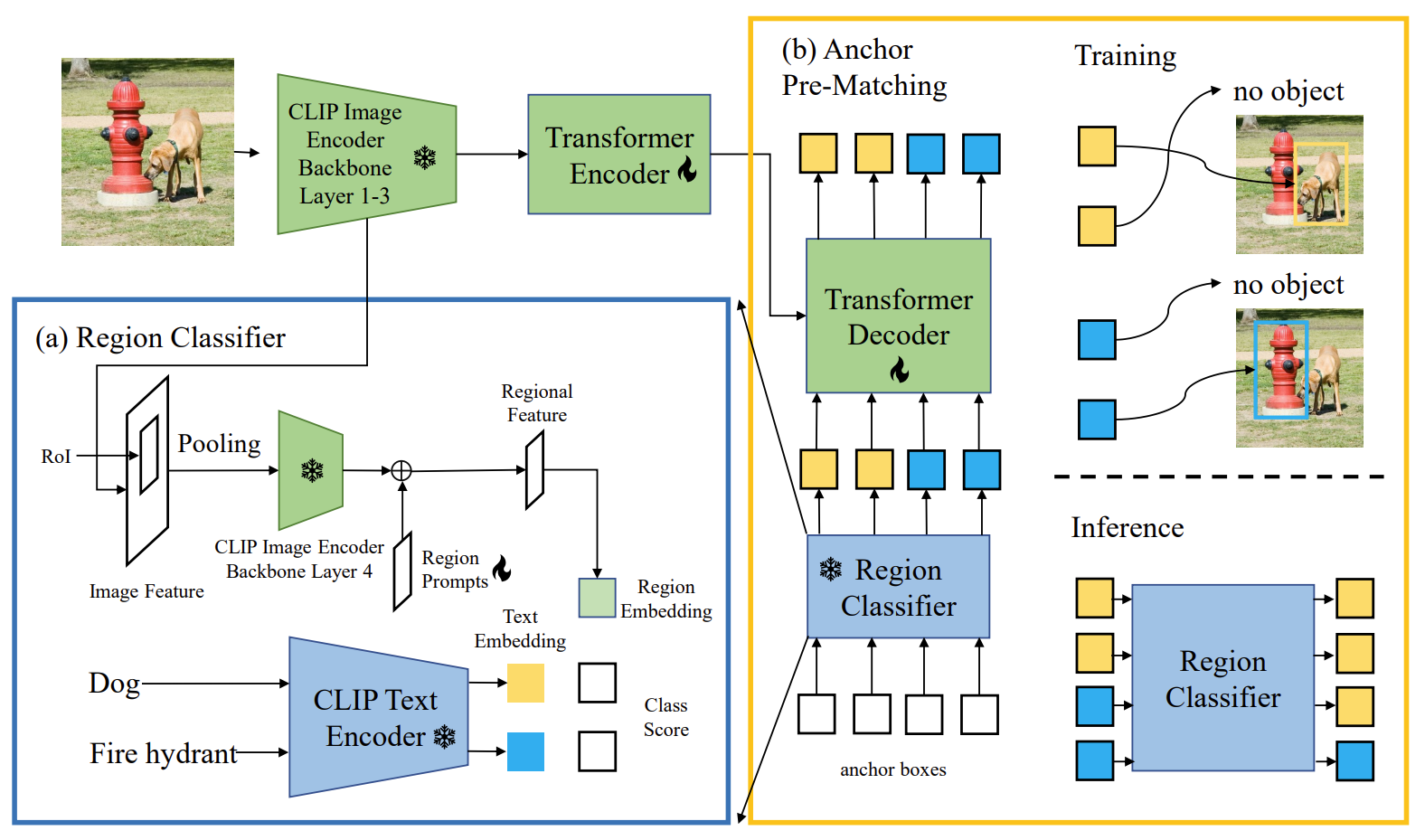
【计算机视觉 | 目标检测】OVD:Open-Vocabulary Object Detection 论文工作总结(共八篇)
文章目录 一、2D open-vocabulary object detection的发展和研究现状二、基于大规模外部图像数据集2.1 OVR-CNN:Open-Vocabulary Object Detection Using Captions,CVPR 20212.2 Open Vocabulary Object Detection with Pseudo Bounding-Box Labels&…...
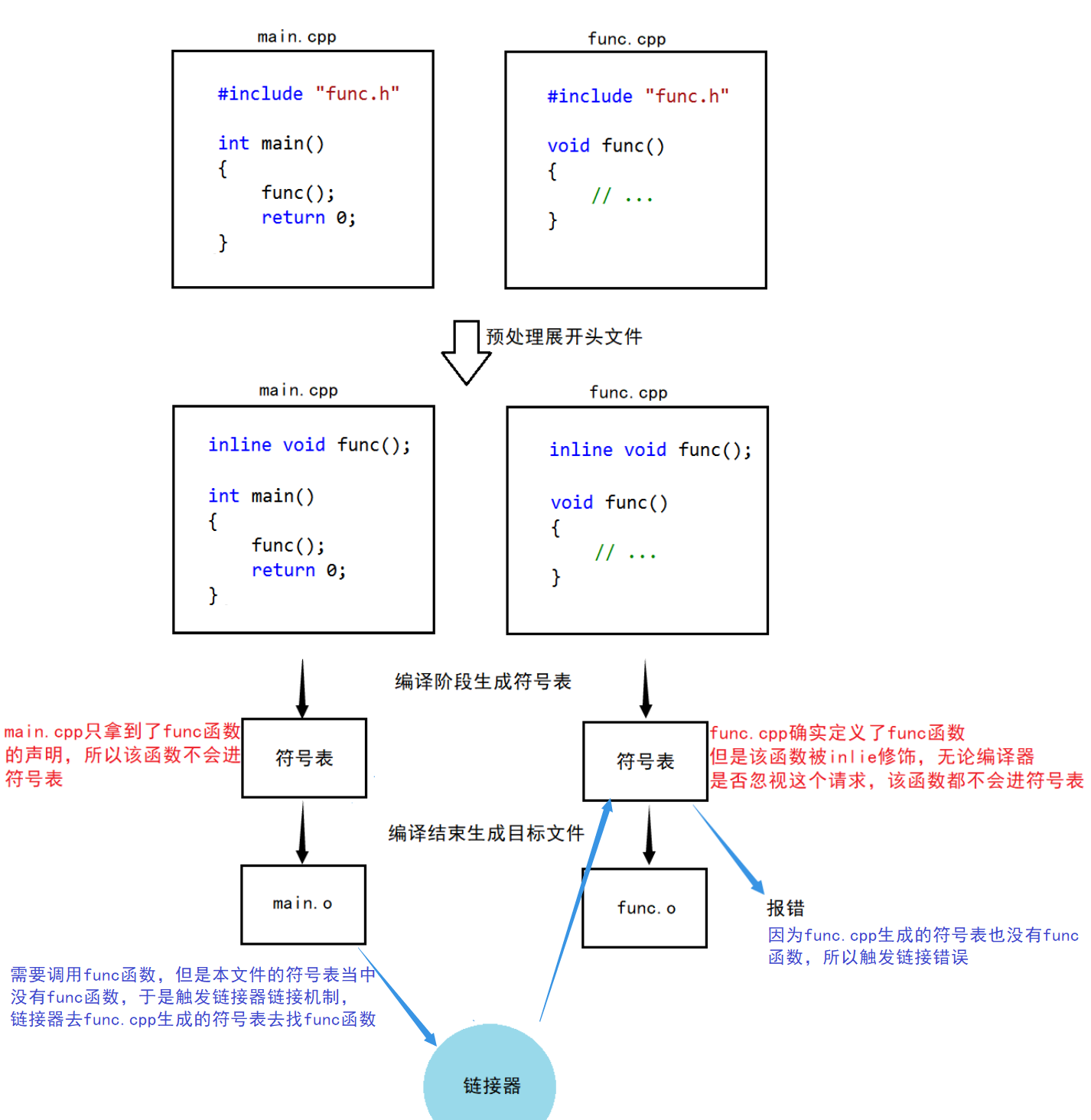
C++入门基础知识[博客园长期更新......]
0.博客园链接 博客的最新内容都在博客园当中,所有内容均为原创(博客园、CSDN同步更新)。 C知识点集合 1.命名空间 在往后的C编程中,将会存在大量的变量和函数,因为有大量的变量和函数,所以C的库会非常多。那么在C语言编程中&a…...
( “树” 之 BST) 501. 二叉搜索树中的众数 ——【Leetcode每日一题】
二叉查找树(BST):根节点大于等于左子树所有节点,小于等于右子树所有节点。 二叉查找树中序遍历有序。 ❓501. 二叉搜索树中的众数 难度:简单 给你一个含重复值的二叉搜索树(BST)的根节点 root…...
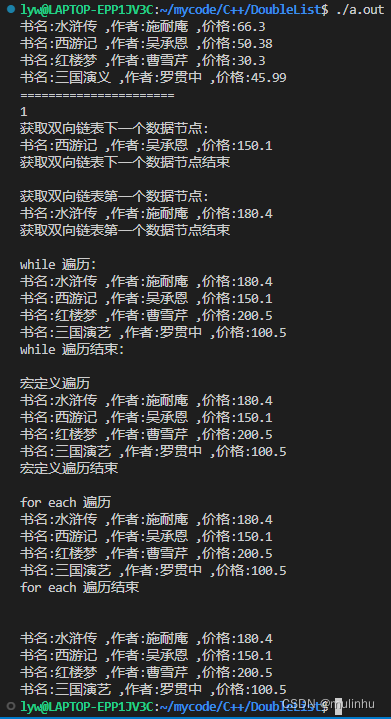
openharmony内核中不一样的双向链表
不一样的双向链表 链表初识别遍历双向链表参考链接 链表初识别 最近看openharmony的内核源码时看到一个有意思的双向链表,结构如下 typedef struct LOS_DL_LIST{struct LOS_DL_LIST *pstPrev; //前驱节点struct LOS_DL_LIST *pstNext; //后继节点 }LOS_DL_LIST;不…...

大文件删除不在回收站里怎么找回
在日常办公中,总会有一些新的文件产生,和用完后的文件清理掉。有时候不小心误删文件也是常有的事。但如果大文件删除不在回收站里怎么找回呢?遇到的小伙伴们请不要别急,只要按照下面的方法做就行了。 正常情况下删除会进入到回收站中&#x…...

Ubuntu22.04部署Pytorch2.0深度学习环境
文章目录 安装Anaconda创建新环境安装Pytorch2.0安装VS CodeUbuntu下实时查看GPU状态的方法小实验:Ubuntu、Windows10下GPU训练速度对比 Ubuntu安装完显卡驱动、CUDA和cudnn后,下面部署深度学习环境。 (安装Ubuntu系统、显卡驱动、CUDA和cudn…...

php的面试集结(会持续更新)
PHP 高级工程面试题汇总 php面试 1.大型的分页查询 发现当表中有很多上万条数据时,越后的数据用limit分页显示就越慢(>2秒),可能是mysql的特性所致。所以花了点时间总结实现了更优解决方案,最终实现毫秒级响应。…...

谁在成为产业经济发展的推车人?
区域发展的新蓝图中,京东云能做什么?它的角色是什么?这个问题背后,隐藏的不仅是京东云自身的能力和价值,更是其作为中国互联网云厂商的代表之一,对“技术产业”的新论证。 作者|皮爷 出品|产业家 关于云…...
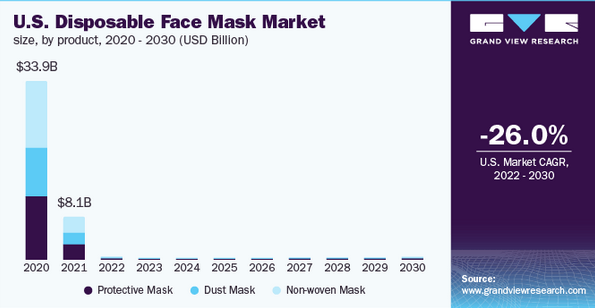
上海无纺布制造商【盈兹】申请纳斯达克IPO上市,募资1100万美元
来源:猛兽财经 作者:猛兽财经 猛兽财经获悉,来自上海的无纺布制造商【盈兹】,近期已向美国证券交易委员会(SEC)提交招股书,申请在纳斯达克IPO上市,股票代码为(ETZ&#…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...
