备份和恢复:确保数据安全
备份和恢复:确保数据安全
在计算机领域中,备份和恢复数据对于确保数据安全至关重要。本文将介绍备份策略概述、使用mysqldump进行备份、使用MySQL Enterprise Backup进行备份、恢复数据以及备份和恢复的最佳实践。
备份策略概述
在制定备份策略时,需要考虑到以下几点:
- 数据重要性:根据数据的重要程度确定备份频率,越重要的数据需要更频繁的备份。
- 备份时间窗口:备份可能会影响业务的正常流程,需要在非业务高峰期备份。
- 备份持续时间和恢复时间:备份持续时间和恢复时间需要根据数据量和备份方式进行估算。
使用mysqldump进行备份
mysqldump是MySQL自带的备份工具,可以备份数据到本地磁盘或者远程服务器。使用mysqldump进行备份的步骤如下:
- 选择需要备份的数据库或者表。
- 指定备份的方式,可以备份到本地磁盘或者远程服务器。
- 选择备份的格式,可以选择sql或者csv格式。
- 执行备份命令。
完成备份后,可以使用备份文件进行数据恢复。
使用MySQL Enterprise Backup进行备份
MySQL Enterprise Backup是MySQL官方推荐的备份工具,可以备份数据到本地磁盘、远程服务器或者云存储。使用MySQL Enterprise Backup进行备份的步骤如下:
- 安装MySQL Enterprise Backup。
- 选择需要备份的数据库或者表。
- 指定备份的方式和格式,可以备份到本地磁盘、远程服务器或者云存储。
- 执行备份命令。
MySQL Enterprise Backup支持增量备份和差异备份,可以大幅减少备份时间和备份文件大小。
恢复数据
在进行数据恢复时,需要注意以下几点:
- 选择合适的备份文件进行恢复,可以根据备份时间和备份内容进行选择。
- 恢复前需要停止相关业务的运行,以免数据覆盖。
- 恢复时需要注意数据的一致性,尽量避免数据丢失和不一致。
备份和恢复的最佳实践
备份和恢复数据是认真对待数据安全的重要步骤,以下是备份和恢复的最佳实践:
- 使用多种备份策略,包括完全备份、增量备份和差异备份。
- 定期测试备份文件的可用性,确保备份文件没有损坏。
- 设置访问控制,确保备份文件只能被授权访问。
- 增量备份必须基于完全备份,差异备份必须基于增量备份。
- 建议使用MySQL官方推荐的备份工具-MySQL Enterprise Backup。
总之,在备份和恢复数据时,需要制定合适的备份策略以及选择合适的备份工具,提高数据库的安全性,避免数据丢失和不一致。
相关文章:

备份和恢复:确保数据安全
备份和恢复:确保数据安全 在计算机领域中,备份和恢复数据对于确保数据安全至关重要。本文将介绍备份策略概述、使用mysqldump进行备份、使用MySQL Enterprise Backup进行备份、恢复数据以及备份和恢复的最佳实践。 备份策略概述 在制定备份策略时&…...
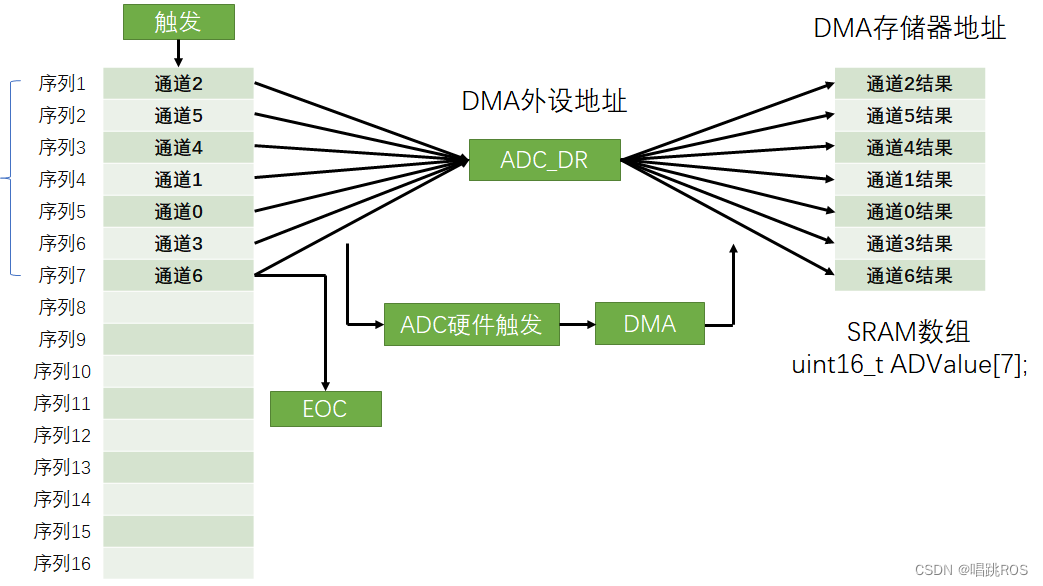
8 DWA(一)
8 DWA DMA简介 DMA(Direct Memory Access)直接存储器存取(可以直接访问32内部存储器,包括内存SRAM,Flash) DMA可以提供外设和存储器或者存储器和存储器之间的高速数据传输,无须CPU干预&#x…...

mysql慢查询日志
概念 MySQL的慢查询日志是MySQL提供的一种日志记录,它用来记录在MySQL中响应时间超过阀值的语句,具体指运行时间超过long_query_time值的SQL,则会被记录到慢查询日志中。long_query_time的默认值为10,意思是运行10秒以上的语句。…...
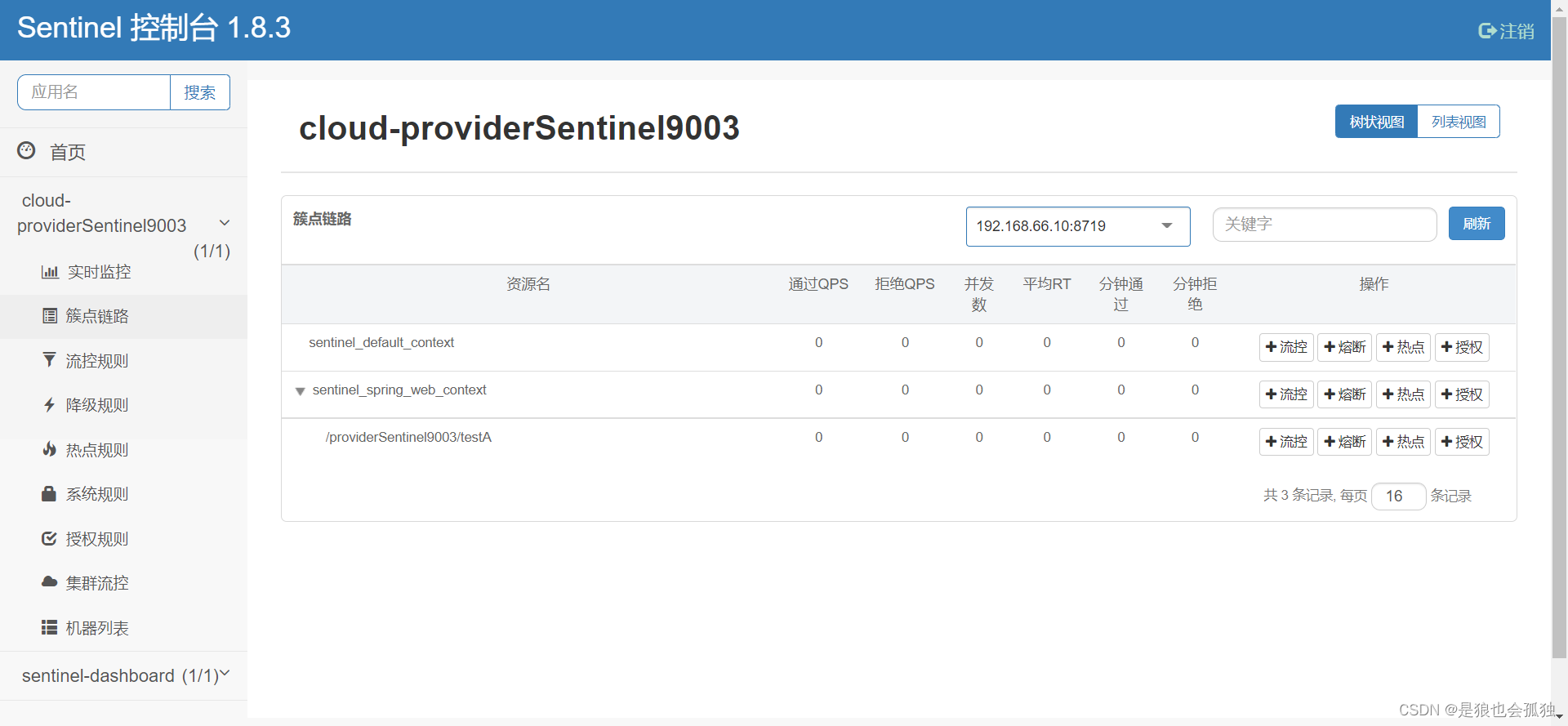
Sentinel介绍及搭建
分布式流量防护 服务雪崩 服务提供者不可用导致服务调用者也跟着不可用,以此类推引起整个链路中的所有微服务都不可用 分布式流量防护 在分布式系统中,服务之间的相互调用会生成分布式流量。如何通过组件进行流量防护,并有效控制流量&…...
最受信任的低代码平台排行榜
近年来,随着数字化转型的兴起,低代码平台获得了大量关注。它允许用户在几乎没有编码知识的情况下创建应用程序,从而使企业能够简化其流程并提高效率。随着低代码平台的日益流行,要确定哪些平台最可靠、最值得信赖并非易事。在本文…...
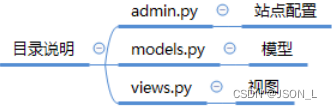
Django框架之创建项目、应用并配置数据库
django3.0框架创建项目、应用并配置数据库 创建项目 进入命令行 新建一个全英文的目录 进入目录 输入命令 django-admin startproject project 项目目录层级 查看当前目录层级 tree /f 目录文件说明 创建数据库 做一个学生管理系统做演示,使用navicat创建数据…...
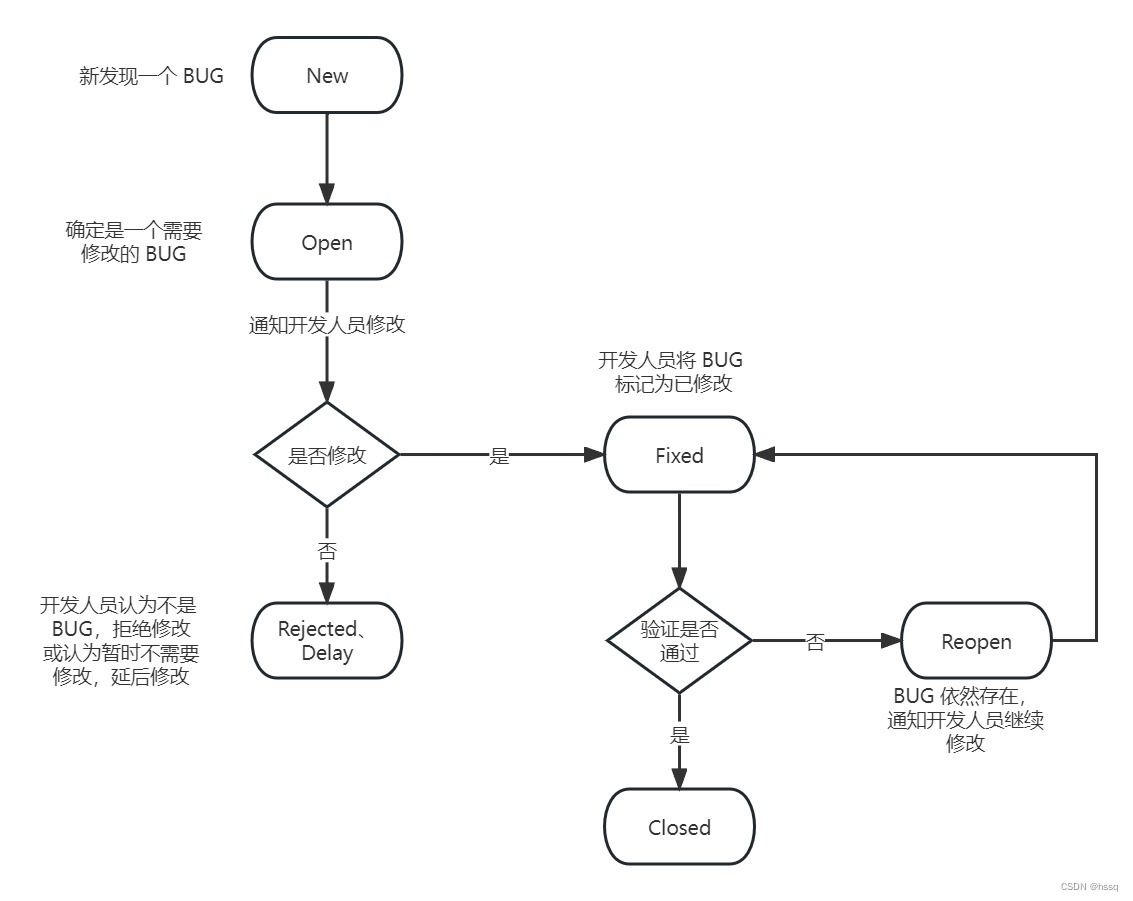
软件测试之基础概念学习篇(需求 + 测试用例 + 开发模型 + 测试模型 + BUG)
文章目录 1. 什么是软件测试2. 软件测试和软件开发的区别3. 软件测试和软件调试的区别4. 什么是需求1)以需求为依据设计测试用例 5. 测试用例是什么6. 什么是 BUG(软件错误)7. 五个开发模型1)瀑布模型2)螺旋模型3&…...
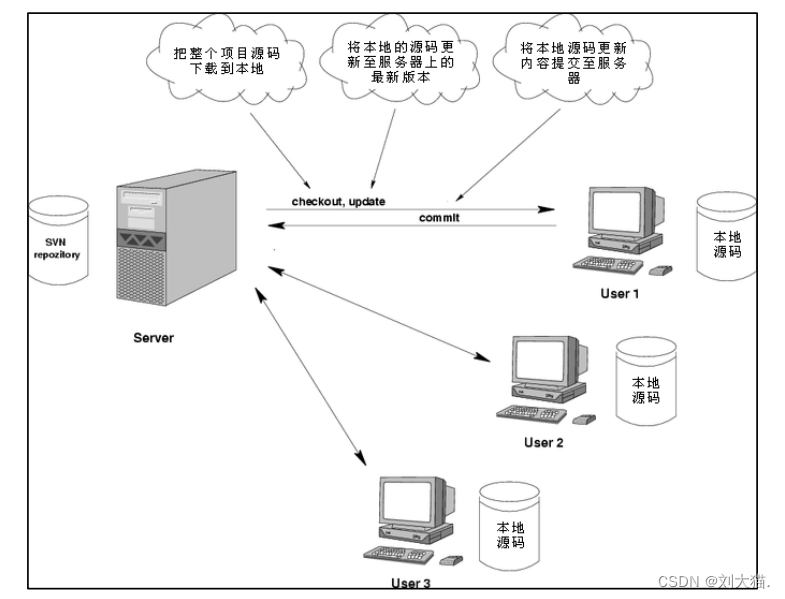
Windows下版本控制器(SVN) - 1、开发中的实际问题+2、版本控制简介
文章目录 基础知识-Windows下版本控制器(SVN)1、开发中的实际问题2、版本控制简介2.1 版本控制[Revision control]2.2 Subversion2.3 Subversion 的优良特性2.4 SVN 的工作原理:2.5 SVN 基本操作 本人其他相关文章链接 基础知识-Windows下版本控制器(SVN) 1、开发中…...

Learning Dynamic Facial Radiance Fields for Few-Shot Talking Head Synthesis 笔记
Learning Dynamic Facial Radiance Fields for Few-Shot Talking Head Synthesis 笔记 摘要 Talking head synthesis is an emerging technology with wide applications in film dubbing, virtual avatars and online education. Recent NeRF-based methods generate more n…...

SpringBoot 项目整合 Redis 教程详解
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

3ASC25H214 DATX130以力控制为基础的装配应用方面已经形成了一个解决方案
3ASC25H214 DATX130以力控制为基础的装配应用方面已经形成了一个解决方案 ABB的机器人解决方案最终选择了IRB6400机器人 ABB的解决方案 ABB一直都在不断地研究和开发机器人应用的新技术,有一部分研究活动是与大学进行合作的,其中一项是ABB的科学家和…...

Java的位运算
目录 1 Java中支持的位运算 2 位运算规则 3 逻辑运算 3.1 与运算(&) 3.2 或运算(|) 3.3 异或运算(^) 3.3 取反运算(~) 4 位移操作 4.1 左移(<<&#…...

FastDFS分布式文件存储
FastDFS文件上传 简介: 主要解决:大容量的文件存储和高并发访问的问题 论坛:https://bbs.chinaunix.net 下载网站:https://sourceforge.net/projects/fastdfs/files/ 安装参考:https://www.cnblogs.com/cxygg/p/1…...

Android的AAC架构
AAC Android Architecture Components的简称,是一套用来搭建具有生命周期感知架构的系列组件,在2017年 GoogleI/O大会上发布。 dependencies {def lifecycle_version "2.2.0"implementation "androidx.lifecycle:lifecycle-livedata-ktx…...

高功率激光切割中不良现象的排除技巧
高功率切割市场现状 随着激光行业的发展和下游产业需求的变化,高功率的激光切割设备已逐渐成为市场关注的热点。高功率激光切割凭着速度和厚度上无可比拟的优势,目前已获得了市场的广泛认可。 但由于高功率激光切割技术尚处于普及的初级阶段,…...

MySQL-----复合查询
文章目录 前言一、基本查询回顾二、 多表查询解决多表查询的思路 三、自连接四、子查询1. 单行子查询2. 多行子查询3. 多列子查询4. 在from子句中使用子查询5. 合并查询5.1 union5.2 unoin all 总结 前言 前面的学习中,对于mysql表的查询都是对一张表进行查询,在实际开发中这远…...
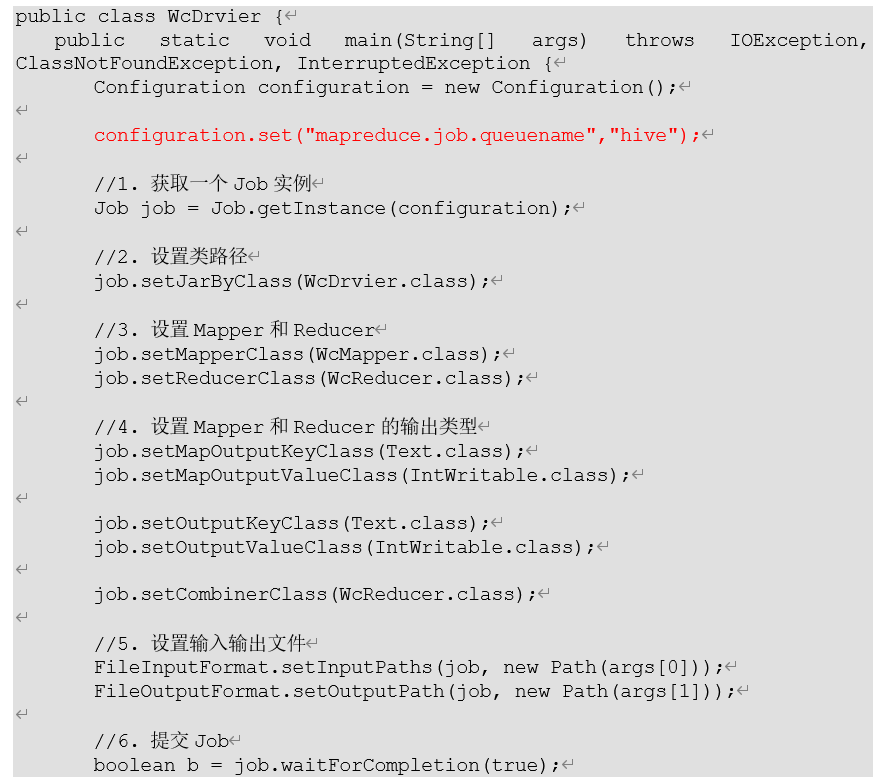
10.Yarn概述
如果说HDFS是存储,则Yarn就是cpu和内存,mapreduce就是程序。 1.基础架构 复习: 1.Container就是一个容器,其中封装了需要使用的内存与cpu 2.每当提交一个job,就会产生一个appMaster(总指挥),app Master负责其他container里面的…...

MFC实现背景透明,控件不透明的对话框,且点击图片有事件响应
最终成果:背景半透明、但是控件不透明的对话框。 对话框上用图片代表功能,当点击图片时,响应点击事件,弹出相对应的对话框。 对话框固定大小,不可放大缩小,以免影响图片的显示数量。 步骤一:背景…...

案例01-tlias智能学习辅助系统01-增删改查+参数传递
目录 1、需求说明:实现对部门表和员工表的增删改查 2、环境搭建 3、部门管理 3.1 查询部门 3.2 前后端联调 3.3 删除部门 3.4 新增部门 3.5 根据ID查询数据 3.5 修改部门 总结(Controller层参数接收): 4、员工管理 4.…...

Spring之Bean的配置与实例
Spring之Bean的配置与实例 一、Bean的基础配置1. Bean基础配置【重点】配置说明代码演示运行结果 2. Bean别名配置配置说明代码演示打印结果 3. Bean作用范围配置【重点】配置说明代码演示打印结果 二、Bean的实例化1. Bean是如何创建的2. 实例化Bean的三种方式2.1 构造方法方式…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...
