【计算机基本原理-数据结构】数据结构中树的详解
【计算机基本原理-数据结构】数据结构中树的详解
- 1)总览
- 2)树的相关概念
- 3)二叉树、满二叉树、完全二叉树
- 4)二叉查找树 - BST
- 5)平衡二叉树 - AVL
- 6)红黑树
- 7)哈弗曼树
- 8)B 树
- 9)B+树
- 10)R 树
- 11)总结
- 12)参考文章
1)总览

树是一种数据结构,它是 n(n>=0)个节点的有限集。n=0 时称为空树。n>0 时,有限集的元素构成一个具有层次感的数据结构。

区别于线性表一对一的元素关系,树中的节点是一对多的关系。树具有以下特点:n>0 时,根节点是唯一的,不可能存在多个根节点。每个节点有零个至多个子节点;除了根节点外,每个节点有且仅有一个父节点。根节点没有父节点。
2)树的相关概念
树有许多相关的术语与概念,在学习树的结构之前,我们要熟悉这些概念。
-
子树:除了根节点外,每个子节点都可以分为多个不相交的子树。
-
孩子与双亲:若一个结点有子树,那么该结点称为子树根的"双亲",子树的根是该结点的"孩子"。在图一中,B、H 是 A 的孩子,A 是 B、H 的双亲。
-
兄弟:具有相同双亲的节点互为兄弟,例如 B 与 H 互为兄弟。
-
节点的度:一个节点拥有子树的数目。例如 A 的度为 2,B 的度为 1,C 的度为 3。
-
叶子:没有子树,也即是度为 0 的节点。分支节点: 除了叶子节点之外的节点,也即是度不为 0 的节点。
-
内部节点:除了根节点之外的分支节点。
-
层次:根节点为第一层,其余节点的层次等于其双亲节点的层次加 1。
-
树的高度:也称为树的深度,树中节点的最大层次。
-
有序树:树中节点各子树之间的次序是重要的,不可以随意交换位置。
-
无序树: 树种节点各子树之间的次序是不重要的。可以随意交换位置。
-
森林: 0 或多棵互不相交的树的集合。例如图二中的两棵树为森林。
3)二叉树、满二叉树、完全二叉树
- 二叉树:最多有两棵子树的树被称为二叉树

- 斜树:所有节点都只有左子树的二叉树叫做左斜树,所有节点都只有右子树的二叉树叫做右斜树。(本质就是链表)

- 满二叉树:二叉树中所有非叶子结点的度都是2,且叶子结点都在同一层次上

- 完全二叉树:如果一个二叉树与满二叉树前m个节点的结构相同,这样的二叉树被称为完全二叉树

4)二叉查找树 - BST
二叉查找树(Binary Search Tree)是指一棵空树或者具有下列性质的二叉树:
1、若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值。
2、若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值。
3、任意节点的左、右子树也分别为二叉查找树。
4、没有键值相等的节点。
二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低为 O ( log n ) 。二叉查找树是基础性数据结构,用于构建更为抽象的数据结构,如集合、多重集、关联数组等。

5)平衡二叉树 - AVL
含有相同节点的二叉查找树可以有不同的形态,而二叉查找树的平均查找长度与树的深度有关,所以需要找出一个查找平均长度最小的一棵,那就是平衡二叉树,具有以下性质:
1、要么是棵空树,要么其根节点左右子树的深度之差的绝对值不超过 1。
2、其左右子树也都是平衡二叉树。
3、二叉树节点的平衡因子定义为该节点的左子树的深度减去右子树的深度。则平衡二叉树的所有节点的平衡因子只可能是 -1,0,1。

6)红黑树
红黑树也是一种自平衡的二叉查找树。
1、每个结点要么是红的要么是黑的。(红或黑)
2、根结点是黑的。(根黑)
3、每个叶结点(叶结点即指树尾端NIL指针或NULL结点)都是黑的。(叶黑)
4、如果一个结点是红的,那么它的两个儿子都是黑的。 (红子黑)
5、对于任意结点而言,其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点。(路径下黑相同)

用法最广:
-
Java Concurrent HashMap & TreeMap
-
C++ STL:map & set
-
Linux 进程调度 Completely Fair Scheduler,用红黑树管理进程控制块
-
epoll 在内核中的实现,用红黑树管理事件块
-
nginx 中,用红黑树管理timer等
7)哈弗曼树
哈夫曼又称最优二叉树。是一种带权路径长度最短的二叉树,一般可以按下面步骤构建:
1、将所有左,右子树都为空的作为根节点。
2、在森林中选出两棵根节点的权值最小的树作为一棵新树的左,右子树,且置新树的附加根节点的权值为其左,右子树上根节点的权值之和。注意,左子树的权值应小于右子树的权值。
3、从森林中删除这两棵树,同时把新树加入到森林中。
4、重复2,3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。

8)B 树
B 树(英语: B-tree)是一种自平衡的树,能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作,都在对数时间内完成。B 树,概括来说是一种自平衡的 m 阶树,与自平衡二叉查找树不同,B 树适用于读写相对大的数据块的存储系统,例如磁盘。
1、根结点至少有两个子女。
2、每个中间节点都包含 k-1 个元素和 k 个孩子,其中 m/2 <= k <= m。
3、每一个叶子节点都包含 k-1 个元素,其中 m/2 <= k <= m。
4、所有的叶子结点都位于同一层。
5、每个节点中的元素从小到大排列,节点当中 k-1 个元素正好是k个孩子包含的元素的值域分划。
B - Tree 中的每个节点根据实际情况可以包含大量的关键字信息和分支,如下图所示为一个 3 阶的 B - Tree:

9)B+树
B + 树是一种树数据结构,通常用于关系型数据库(如Mysql)和操作系统的文件系统中。
1、B + 树的特点是能够保持数据稳定有序,其插入与修改拥有较稳定的对数时间复杂度。
2、B + 树元素自底向上插入,这与二叉树恰好相反。
3、在 B 树基础上,为叶子结点增加链表指针(B + 树叶子有序链表),所有关键字都在叶子结点中出现,非叶子结点作为叶子结点的索引;B + 树总是到叶子结点才命中。
4、B + 树的非叶子节点不保存数据,只保存子树的临界值(最大或者最小),所以同样大小的节点,B + 树相对于 B 树能够有更多的分支,使得这棵树更加矮胖,查询时做的 IO 操作次数也更少。
将上一节中的 B - Tree 优化,由于 B + Tree 的非叶子节点只存储键值信息,假设每个磁盘块能存储 4 个键值及指针信息,则变成 B + Tree 后其结构如下图所示:
 )
)
10)R 树
R 树是用来做空间数据存储的树状数据结构。例如给地理位置,矩形和多边形这类多维数据建立索引。
R 树的核心思想是聚合距离相近的节点并在树结构的上一层将其表示为这些节点的最小外接矩形(MBR),这个最小外接矩形就成为上一层的一个节点。因为所有节点都在它们的最小外接矩形中,所以跟某个矩形不相交的查询就一定跟这个矩形中的所有节点都不相交。叶子节点上的每个矩形都代表一个对象,节点都是对象的聚合,并且越往上层聚合的对象就越多。也可以把每一层看做是对数据集的近似,叶子节点层是最细粒度的近似,与数据集相似度 100%,越往上层越粗糙。
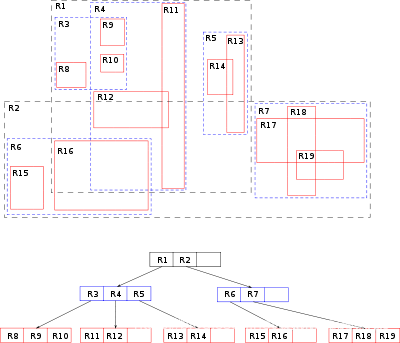
11)总结
我们知道,实际应用当中,我们经常使用的是查找和排序操作,这在我们的各种管理系统、数据库系统、操作系统等当中,十分常用。
数组:数组的下标寻址十分迅速,但计算机的内存是有限的,故数组的长度也是有限的,实际应用当中的数据往往十分庞大;而且无序数组的查找最坏情况需要遍历整个数组;后来人们提出了二分查找,二分查找要求数组的构造一定有序,二分法查找解决了普通数组查找复杂度过高的问题。任何一种数组无法解决的问题就是插入、删除操作比较复杂,因此,在一个增删查改比较频繁的数据结构中,数组不会被优先考虑。
普通链表:由于链表的结构特点被证明根本不适合进行查找。
哈希表:哈希表是数组和链表的折中,同时它的设计依赖散列函数的设计,数组不能无限长、链表也不适合查找,所以也不适合大规模的查找
二叉查找树:二叉查找树可能退化成链表,同样不适合进行查找
AVL 树:AVL树是为了解决可能退化成链表问题,但是 AVL 树的旋转过程非常麻烦,因此插入和删除很慢,也就是构建AVL树比较麻烦。
红黑树:红黑树是平衡二叉树和AVL树的折中,因此是比较合适的。集合类中的Map、关联数组具有较高的查询效率,它们的底层实现就是红黑树。
多路查找树:大规模数据存储中,实现索引查询这样一个实际背景下,树节点存储的元素数量是有限的(如果元素数量非常多的话,查找就退化成节点内部的线性查找了),这样导致二叉查找树结构由于树的深度过大而造成磁盘 I/O 读写过于频繁,进而导致查询效率低下。
B 树:与自平衡二叉查找树不同,B 树适用于读写相对大的数据块的存储系统,例如磁盘。它的应用是文件系统及部分非关系型数据库索引。
B + 树:在 B 树基础上,为叶子结点增加链表指针(B + 树叶子有序链表),所有关键字都在叶子结点中出现,非叶子结点作为叶子结点的索引;B + 树总是到叶子结点才命中。通常用于关系型数据库(如 Mysql)和操作系统的文件系统中。
B * 树:是 B + 树的变体,在 B + 树的非根和非叶子结点再增加指向兄弟的指针, 在 B + 树基础上,为非叶子结点也增加链表指针,将结点的最低利用率从 1/2 提高到 2/3。
R 树:是用来做空间数据存储的树状数据结构。例如给地理位置,矩形和多边形这类多维数据建立索引。
Trie 树:Trie 树是自然语言处理中最常用的数据结构,很多字符串处理任务都会用到。Trie 树本身是一种有限状态自动机,还有很多变体。什么模式匹配、正则表达式,都与这有关。
针对大量数据,如果在内存中作业优先考虑红黑树(map,set 之类多为 RB-tree 实现),如果在硬盘中作业优先考虑 B 系列树(B +,B,B *)
12)参考文章
-
各种二叉树的介绍
-
二叉树、二叉搜索树、平衡二叉树、B树、B+树的精确定义和区别探究
-
数据结构之树
-
B + Tree原理及 Mysql 的索引分析
相关文章:

【计算机基本原理-数据结构】数据结构中树的详解
【计算机基本原理-数据结构】数据结构中树的详解 1)总览2)树的相关概念3)二叉树、满二叉树、完全二叉树4)二叉查找树 - BST5)平衡二叉树 - AVL6)红黑树7)哈弗曼树8)B 树9)…...
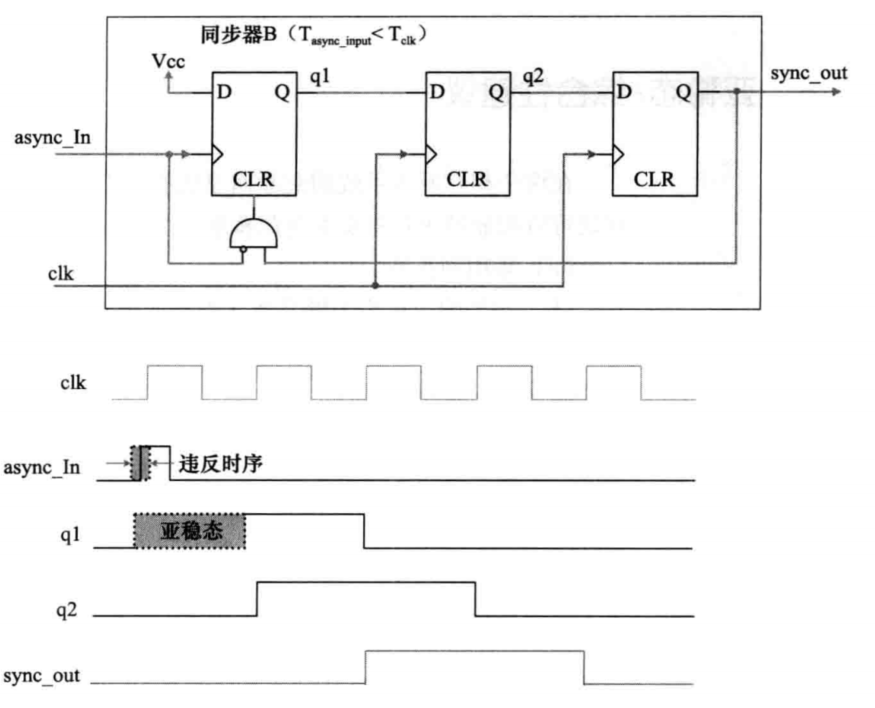
数字设计小思 - D触发器与死缠烂打的亚稳态
前言 本系列整理数字系统设计的相关知识体系架构,为了方便后续自己查阅与求职准备。在FPGA和ASIC设计中,D触发器是最常用的器件,也可以说是时序逻辑的核心,本文根据个人的思考历程结合相关书籍内容和网上文章,聊一聊D…...

Notes/Domino 11.0.1FP7以及在NAS上安装Domino等
大家好,才是真的好。 目前HCL在还是支持更新的Notes/Domino主要是三个版本,V10、11和12,这不,上周HCL Notes/Domino 11.0.1居然推出了FP7补丁包程序。 从V10.0.1开始,Domino的FP补丁包程序主要是用来修复对应主要版本中的一些问…...
【VM服务管家】VM4.x算子SDK开发_3.3 模块工具类
目录 3.3.1 位置修正:位置修正算子工具的使用方法3.3.2 模板保存:实现模板自动加载的方法3.3.3 模板匹配: 获取模板匹配框和轮廓点的方法3.3.4 模板训练:模板训练执行完成的判断方法3.3.5 图像相减:算子SDK开发图像相减…...
Aspose.Pdf使用教程:在PDF文件中添加水印
Aspose.PDF 是一款高级PDF处理API,可以在跨平台应用程序中轻松生成,修改,转换,呈现,保护和打印文档。无需使用Adobe Acrobat。此外,API提供压缩选项,表创建和处理,图形和图像功能&am…...
H.264/AVC加密----选择加密
文献学习: 《Data Hiding in Encrypted H.264/AVC Video Streams by Codeword Substitution》 期刊:IEEE TRANSACTIONS ON INFORMATION FORENSICS AND SECURITY 简介 通过分析H.264/AVC编解码器的特性,提出了三个敏感部分(IPM、MVD和残差系…...

WuThreat身份安全云-TVD每日漏洞情报-2023-04-26
漏洞名称:Google Android 命令注入漏洞 漏洞级别:高危 漏洞编号:CVE-2023-20964,CNNVD-202303-538 相关涉及:None 漏洞状态:POC 参考链接:https://tvd.wuthreat.com/#/listDetail?TVD_IDTVD-2023-05794 漏洞名称:OpenSSL RSA 解密时间差异 漏洞级别:中危 漏洞编号:CVE-2022-4…...

剑指 Offer第二版:1~n 整数中 1 出现的次数、51. 数组中的逆序对、56 - II. 数组中数字出现的次数 II
剑指 Offer第二版 43. 1~n 整数中 1 出现的次数51. 数组中的逆序对56 - II. 数组中数字出现的次数 II 43. 1~n 整数中 1 出现的次数 题目:输入一个整数 n ,求1~n这n个整数的十进制表示中1出现的次数。 例如,…...
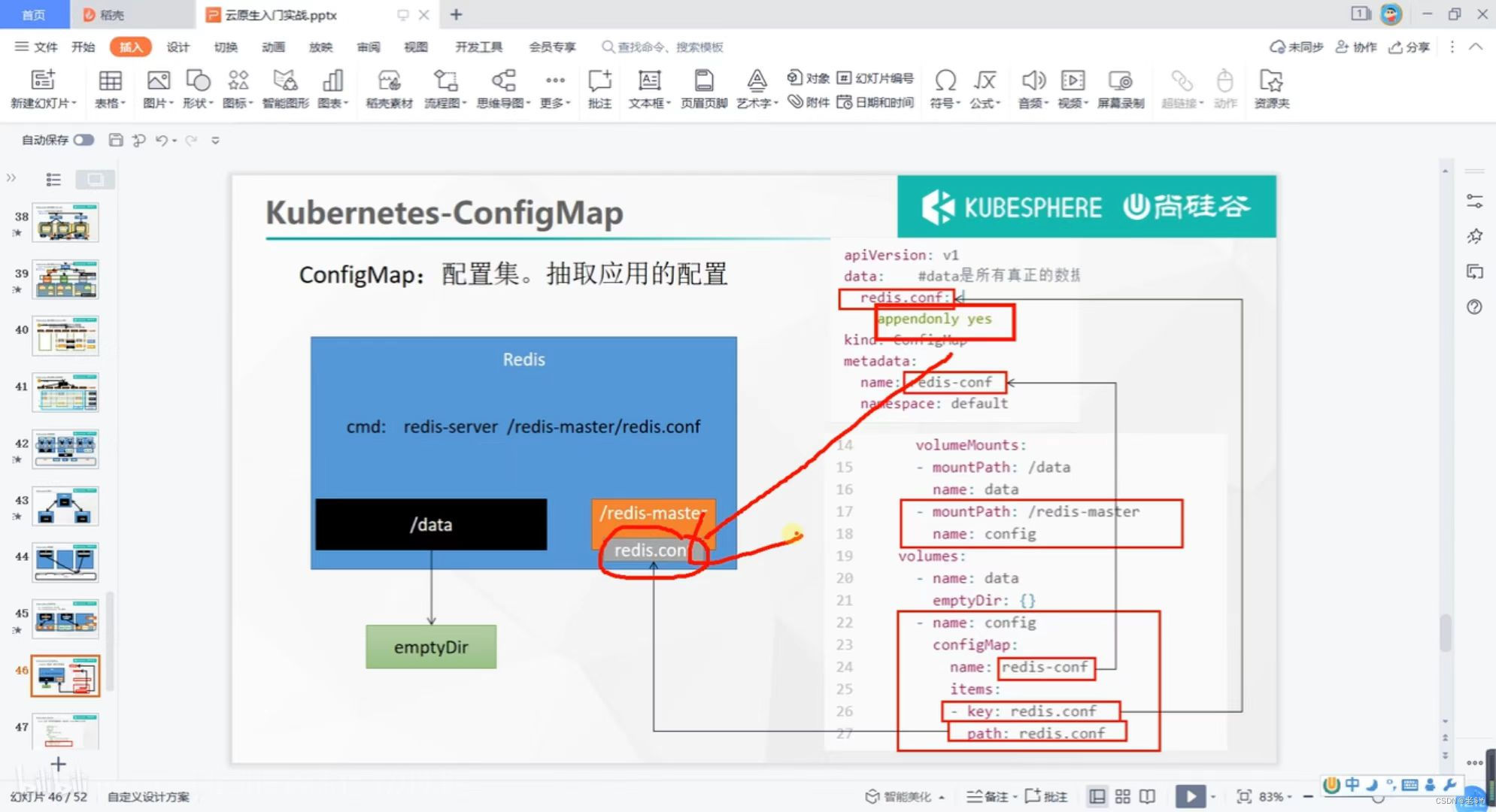
云原生-k8s核心概念(pod,deploy,service,ingress,configmap,volume)
Gitee-k8s学习 云原生实战-kubernetes核心实战 namespace Namespace是kubernetes系统中的一种非常重要资源,它的主要作用是用来实现多套环境的资源隔离或者多租户的资源隔离 Pod Pod可以认为是容器的封装,一个Pod中可以存在一个或者多个容器。 De…...

他工作10年,老板却让他走人
大家好,我是五月,一个编程街溜子。 二狗被裁了,他在公司待了快十年,他想留下来,老板却让他走。 我和他一样困惑。 他985毕业,工作中有从0开始一个项目直到日活过千万,也有过参与顶级产品核心…...

vpp怎么写node
VPP(Vector Packet Processing)是一个高性能的数据平面开源项目,用于构建网络功能虚拟化(NFV)和软件定义网络(SDN)解决方案。它由Cisco开发,并在Apache 2.0许可下发布。 在VPP中&am…...
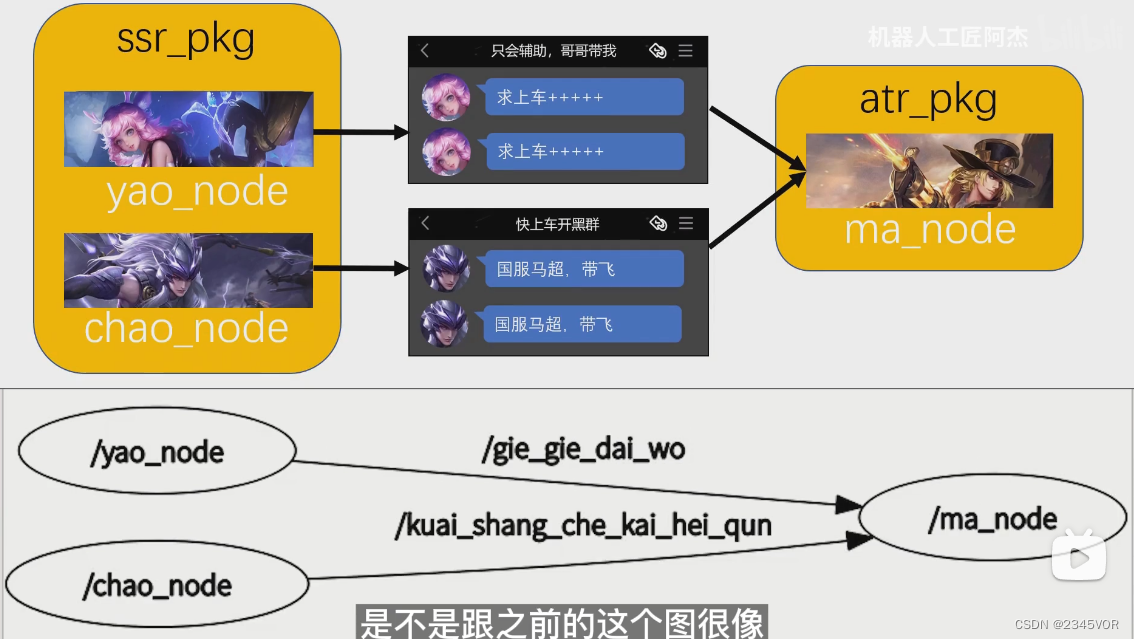
【4. ROS的主要通讯方式:Topic话题与Message消息】
【4. ROS的主要通讯方式:Topic话题与Message消息】 1. 前言1.1 王者解释结点通讯:1.2 通讯小结 2. 灵活的Topic话题图解2.1 话题注意细节2.2 外延补充 3. Message消息图解3.1 消息类型3.2 查看标准消息类型std_msgs 4. 使用C实现Publisher发布者4.1 发布…...

【react全家桶学习】react中组件定义及state属性(超详/必看)
函数式组件定义及特点 定义(核心就是一个函数,返回虚拟dom): import React from reactexport default function index() {return <div>index</div> }特点: 1、适用于【简单组件】的定义2、是一个函数&a…...

如何以产品经理思维打造一所高品质学校?
学校的建设与管理真不是一件容易事。2023年03月17日,山东菏泽市曹县一家长投诉某中学课业繁重,孩子经常写作业到半夜;2023年4月4日,张先生在华龙网重庆网络问政平台投诉万州区某中学伙食差,指出“发灰的洋葱࿰…...

根治Spring中使用Mongo时报错InvalidMongoDbApiUsageException
文章目录 And Or迷惑原因 告别InvalidMongoDbApiUsageException问题简单解决根本解决修改源码 代码(省流,可以直接看这里) And Or 很多时候都需要进行逻辑的与或操作,但是spring当中自带的操作并不好用,于是做了相关的改进&#…...

【计算机组成原理】数据的表示和运算·进位计数制
🚩 本文已收录至专栏:计算机基础 我们可以通过显示屏看到各种形式的数据信息,但数据是如何在计算机中表示呢?运算器又是如何实现数据的算数、逻辑运算? 十进制数是最适合我们日常使用的一种计数方式,除此之…...
)
C++ Primer第五版_第十四章习题答案(21~30)
文章目录 练习14.21练习14.22头文件CPP文件 练习14.23头文件CPP文件 练习14.24头文件CPP文件 练习14.25练习14.26练习14.27练习14.28练习14.29练习14.30 练习14.21 编写 Sales_data 类的 和 运算符,使得 执行实际的加法操作而 调用。相比14.3节和14.4节对这两个运…...

服务器性能调优
硬件 如果是硬件瓶颈就换硬件 (包括CPU、内存、网卡) 软件 如果是方案架构设计有问题就换方案,比如mysql、redis方案有问题 建议先 top 看下软件瓶颈在哪,CPU、内存、网络(netstat),哪个进程占…...
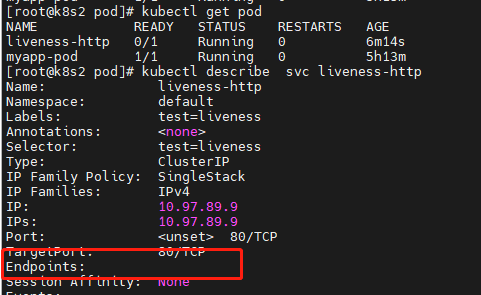
带你深入学习k8s--(三) pod 管理
目录 一、简介 1、什么是pod 2、为什么要有pod 二、pod的分类 0、pod常用命令命令 1、准备镜像 2、自主式pod 3、控制器创建pod 4、扩容pod数量 5、通过service暴露pod(负载均衡,自动发起) 6、更新应用版本 三、编写yaml文件 四、Pod生命周期…...

前端系列11集-ES6 知识总结
ES Module 优点 静态分析 浏览器和 Node 都支持 浏览器的新 API 能用模块格式提供 不再需要对象作为命名空间 export 用于规定模块的对外接口 输出的接口与其对应的值是动态绑定关系可以取到模块内部实时的值 import 用于输入其他模块提供的功能 具有提升效果,会提升…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
