【MySQL高级】——InnoDB索引MyISAM索引
一、索引概述
MySQL官方对索引的定义为:索引(Index)是帮助MySQL高效获取数据的数据结构。 索引的本质:索引是数据结构。你可以简单理解为“排好序的快速查找数据结构”,满足特定查找算法。 这些数据结构以某种方式指向数据, 这样就可以在这些数据结构的基础上实现 高级查找算法 。
二、索引的优缺点
<1> 优点
(1)类似大学图书馆建书目索引,提高数据检索的效率,降低数据库的IO成本 ,这也是创建索引最主要的原因。
(2)通过创建唯一索引,可以保证数据库表中每一行 数据的唯一性 。
(3)在实现数据的参考完整性方面,可以加速表和表之间的连接 。换句话说,对于有依赖关系的子表和父表联合查询时,可以提高查询速度。
(4)在使用分组和排序子句进行数据查询时,可以显著减少查询中分组和排序的时 间 ,降低了CPU的消耗。
<2> 缺点
(1)创建索引和维护索引要耗费时间 ,并且随着数据量的增加,所耗费的时间也会增加。
(2)索引需要占磁盘空间 ,除了数据表占数据空间之外,每一个索引还要占一定的物理空间,存储在磁盘上 ,如果有大量的索引,索引文件就可能比数据文件更快达到最大文件尺寸。
(3)虽然索引大大提高了查询速度,同时却会降低更新表的速度 。当对表中的数据进行增加、删除和修改的时候,索引也要动态地维护,这样就降低了数据的维护速度。 因此,选择使用索引时,需要综合考虑索引的优点和缺点。
三、InnoDB的索引方案
<1> 基本结构
1. 行格式
就是一条数据库表中的一行数据的格式,简化Compact 行格式如下:
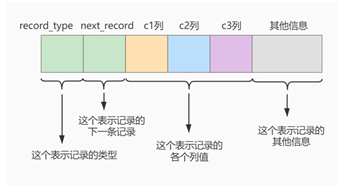
<1> record_type
记录头信息的一项属性,表示记录的类型
0 表示普通记录、1表示目录项记录 、2 表示最小记录、 3 表示最大记录
<2> next_record
记录头信息的一项属性,表示下一条地址相对于本条记录的地址偏移量,我们用箭头来表明下一条记录是谁。
<3> 各个列的值
这里只记录在 index_demo 表中的三个列,分别是 c1 、 c2 和 c3 。
<4> 其他信息
除了上述3种信息以外的所有信息,包括其他隐藏列的值以及记录的额外信息。
2. 数据项页

<1> 页内存放表中一行记录的全部数据,数据间根据索引列有序。
<2> 标记最大值,最小值
<3> 可以根据二分法 快速定位到数据
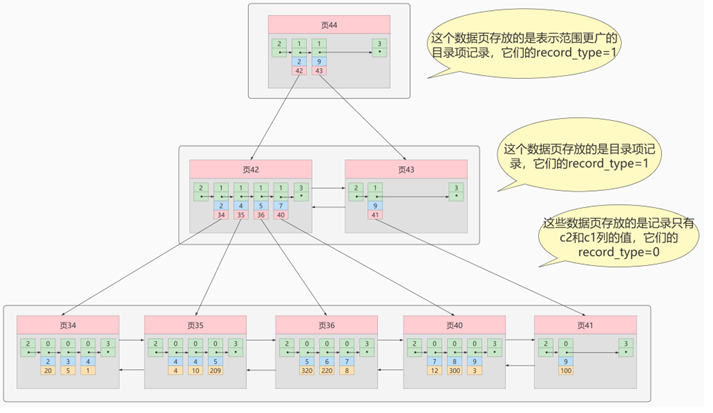
3. 目录项页
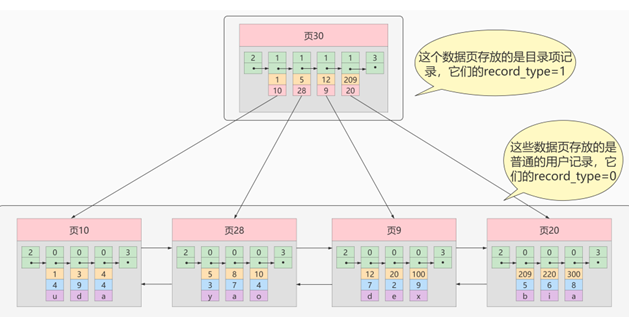
<1> 目录项页存放数据项页的【地址和索引列最小值】
<2> 目录项记录的 record_type 值是1
<3> 目录项记录只有索引列值和数据项页的目录地址两个列
<4> 目录项页内的数据也是根据索引列有序,可以根据二分法快速定位到数据
4. B+Tree
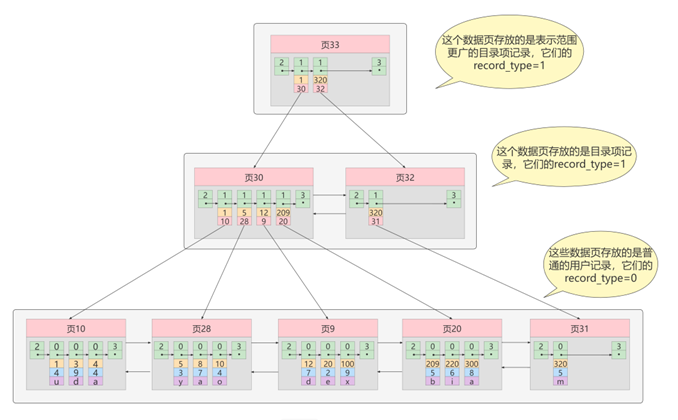
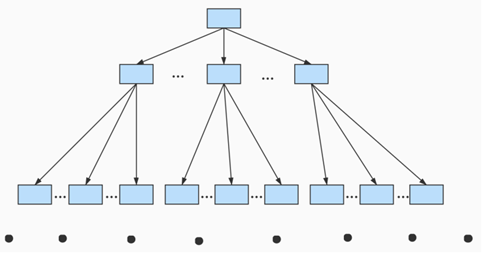
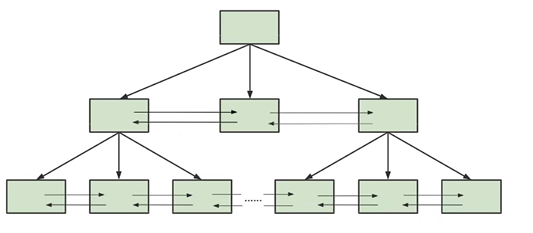
<1> 特性
- 叶子节点内数据递增有序,形成有序列表
- 非叶子节点内的数据指向叶子节点
- 非叶子节点在叶子节点中是最大(或最小)元素。
- B+树的叶子结点都是相连的,因此对整棵树的遍历只需要一次线性遍历叶子结点即可。而且由于数据顺序排列并且相连,所以便于区间查找和搜索。而B树则需要进行每一层的递归遍历。
<2> 性能分析
一个B+树的节点其实可以分成好多层,规定最下边的那层,也就是存放我们用户记录的那层为第 0 层,之后依次往上加。之前我们做了一个非常极端的假设:存放用户记录的页 最多存放3条记录 ,存放目录项记录的页 最多存放4条记录 。其实真实环境中一个页存放的记录数量是非常大的,假设所有存放用户记录的叶子节点代表的数据页可以存放 100条用户记录 ,所有存放目录项记录的内节点代表的数据页可以存
放 1000条目录项记录 ,那么:
如果B+树只有1层,也就是只有1个用于存放用户记录的节点,最多能存放 100 条记录。
如果B+树有2层,最多能存放 1000×100=10,0000 条记录。
如果B+树有3层,最多能存放 1000×1000×100=1,0000,0000 条记录。
如果B+树有4层,最多能存放 1000×1000×1000×100=1000,0000,0000 条记录。
你的表里能存放 100000000000 条记录吗?所以一般情况下,我们 用到的B+树都不会超过4层 ,那我们通过主键值去查找某条记录最多只需要做4个页面内的查找(查找3个目录项页和一个用户记录页),又因为在每个页面内有所谓的 Page Directory (页目录),所以在页面内也可以通过 二分法 实现快速定位记录。
<2> 聚簇索引&非聚簇索引
1. 聚簇索引(主键索引)
<1> 特点
- 使用记录主键值的大小进行记录和页的排序,这包括三个方面的含义:
页内的记录是按照主键的大小顺序排成一个单向链表 。
各个存放用户记录的页 也是根据页中用户记录的主键大小顺序排成一个 双向链表 。
存放目录项记录的页分为不同的层次,在同一层次中的页也是根据页中目录项记录的主键 大小顺序排成一个 双向链表 。 - B+树的 叶子节点存储的是完整的用户记录。 所谓完整的用户记录,就是指这个记录中存储了所有列的值(包括隐藏列)。
- 我们把具有这两种特性的B+树称为聚簇索引,所有完整的用户记录都存放在这个聚簇索引的叶子节点处。这种聚簇索引并不需要我们在MysQL语句中显式的使用INDEX语句去创建,InnoDB存储引擎会自动的为我们创建聚簇索引。
<2> 优点
数据访问更快 ,因为聚簇索引将索引和数据保存在同一个B+树中,因此从聚簇索引中获取数据比非聚簇索引更快
聚簇索引对于主键的 排序查找 和 范围查找 速度非常快
按照聚簇索引排列顺序,查询显示一定范围数据的时候,由于数据都是紧密相连,数据库不用从多个数据块中提取数据,所以 节省了大量的io操作 。
<3> 缺点
插入速度严重依赖于插入顺序 ,按照主键的顺序插入是最快的方式,否则将会出现页分裂,严重影响性能。因此,对于InnoDB表,我们一般都会定义一个自增的ID列为主键
更新主键的代价很高 ,因为将会导致被更新的行移动。因此,对于InnoDB表,我们一般定义主键为不可更新
二级索引访问需要两次索引查找 ,第一次找到主键值,第二次根据主键值找到行数据
<4> 限制

2. 非聚簇索引(二级索引、辅助索引)
<1> 非聚簇索引

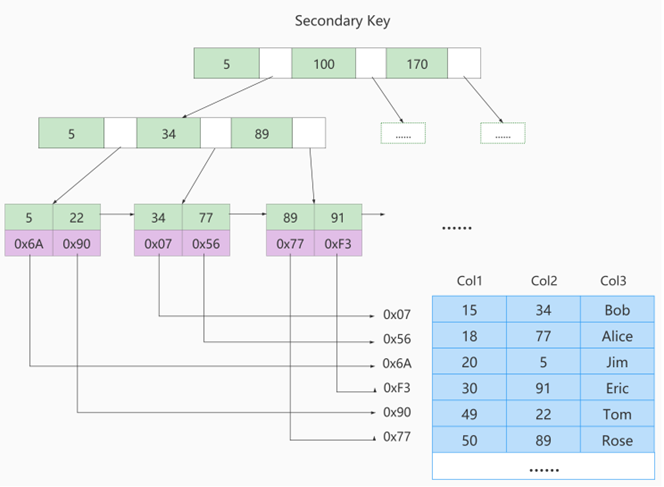
<2> 回表
我们根据这个以索引列大小排序的B+树只能确定我们要查找记录的主键值,所以如果我们想根 据索引列的值查找到完整的用户记录的话,仍然需要到 聚簇索引 中再查一遍,这个过程称为 回表 。也就 是根据索引列的值查询一条完整的用户记录需要使用到 2 棵B+树!
<3> 联合索引

<4> 与聚簇索引的不同
- 页内的记录是按照索引列的大小顺序排成一个单向链表。
- 各个存放用户记录的页也是根据页中记录的索引列大小顺序排成一个双向链表。
- 存放目录项记录的页分为不同的层次,在同一层次中的页也是根据页中目录项记录的索引列大小顺序排成一个双向链表。
- 数据项页存储的不是完整的数据。只是索引列和主键列
- 目录项页存储的索引列、主键列和页号
<3> 注意
1. 根节点不变

2. 内节点中目录项记录的唯一性
目录项页中的每个数据要唯一,添加主键来实现唯一
3. 一个页面最少存储2条记录

四、MyISAM的索引方案
MyISAM引擎使用 B+Tree 作为索引结构,叶子节点的data域存放的是 数据记录的地址 。

<1> 主键索引


<2> 二级索引

五、MyISAM与InnoDB对比
<1> 对比
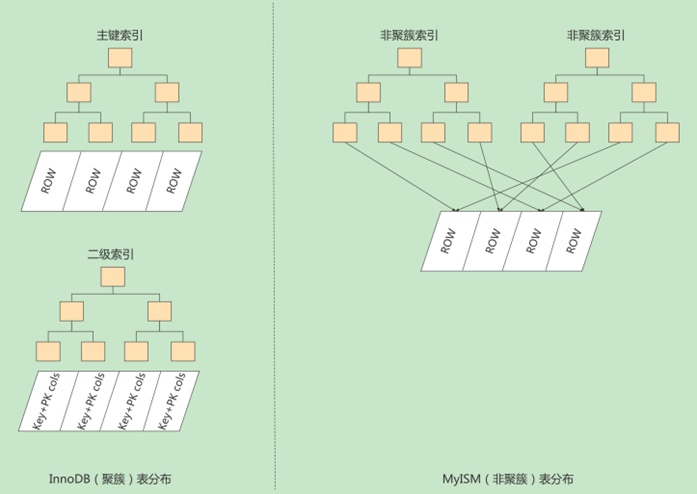
- 在InnoDB存储引擎中,我们只需要根据主键值对 聚簇索引 进行一次查找就能找到对应的记录,而在MyISAM 中却需要进行一次 回表 操作,意味着MyISAM中建立的索引相当于全部都是 二级索引 。
- InnoDB的数据文件本身就是索引文件,而MyISAM索引文件和数据文件是 分离的 ,索引文件仅保存数据记录的地址。
- InnoDB的非聚簇索引data域存储相应记录 主键的值 ,而MyISAM索引记录的是 地址 。换句话说,InnoDB的所有非聚簇索引都引用主键作为data域。
- MyISAM的回表操作是十分 快速 的,因为是拿着地址偏移量直接到文件中取数据的,反观InnoDB是通过获取主键之后再去聚簇索引里找记录,虽然说也不慢,但还是比不上直接用地址去访问。
- InnoDB要求表 必须有主键 ( MyISAM可以没有 )。如果没有显式指定,则MySQL系统会自动选择一个可以非空且唯一标识数据记录的列作为主键。如果不存在这种列,则MySQL自动为InnoDB表生成一个隐含字段作为主键,这个字段长度为6个字节,类型为长整型。
<2> 索引优化举例

六、索引的代价
<1> 空间代价
每建立一个索引都要为它建立一棵B+树,每一棵B+树的每一个节点都是一个数据页,一个页默认会 占用 16KB 的存储空间,一棵很大的B+树由许多数据页组成,那就是很大的一片存储空间。
<2> 时间代价
每次对表中的数据进行 增、删、改 操作时,都需要去修改各个B+树索引。而且我们讲过,B+树每层节点都是按照索引列的值 从小到大的顺序排序 而组成了 双向链表 。不论是叶子节点中的记录,还是内节点中的记录(也就是不论是用户记录还是目录项记录)都是按照索引列的值从小到大的顺序而形成了一个单向链表。而增、删、改操作可能会对节点和记录的排序造成破坏,所以存储引擎需要额外的时间进行一些 记录移位 , 页面分裂 、 页面回收 等操作来维护好节点和记录的排序。如果我们建了许多索引,每个索引对应的B+树都要进行相关的维护操作,会给性能拖后腿。

相关文章:

【MySQL高级】——InnoDB索引MyISAM索引
一、索引概述 MySQL官方对索引的定义为:索引(Index)是帮助MySQL高效获取数据的数据结构。 索引的本质:索引是数据结构。你可以简单理解为“排好序的快速查找数据结构”,满足特定查找算法。 这些数据结构以某种方式指向…...

电影《灌篮高手》观后
上周和同学一起看了电影《灌篮高手》这部电影,个人以前没有看过相关漫画和动画,但记得,看过海报和一些宣传物品,有的衣服上,有文具盒上,也都出现过,而且是在自己小时候,可见当时的影…...

C# .Net 中的同步上下文
.Net 中的同步上下文 【文 / 张赐荣】 什么是同步上下文? 同步上下文(SynchronizationContext)是一个抽象类,它提供了一个基本的功能,用于在不同的同步模型中传播一个同步操作。 同步上下文表示一个代码执行的位置&a…...

3分钟入门:Flex 布局
flex 布局原理 全称 flexible box,弹性布局。 如何开启:为元素添加 display: flex。 开启 flex 布局的元素,称为 flex 容器(flex container),其子元素成为容器成员,称为 flex 项目。 flex 布…...

我想知道,就目前形势而言,学java好还是C++好?
前言 就现实点看看,可以对比现在Java和C的市场占有率,可以看到,到目前为止,Java在国内编程语言的市场仍然是占据着大头,在招聘当中Java的人数占有率仍然是遥遥领先于C,Java目前开阔的市场以及其巨大的岗位…...

Mysql 管理
目录 0 课程视频 1 系统数据库 -> 安装完mysql ->自带四个数据库 2 常用工具 -> 写脚本用 2.1 mysql 客户端工具 2.2 mysqladmin 2.3 mysqlbinlog -> 二进制日志 -> 运维讲解 2.4 mysqlshow 2.5 mysqldump 备份用 ->导出 2.6 mysqlimport/source -…...
)
C#基础(算术运算符)
作用 算术运算符 是用于 数值类型变量计算的运算符 它的返回结果是数值 赋值符号 // // 关键知识点: // 先看右侧 再看左侧 把右侧的值赋值给左侧的值 int myAge 18; 算术运算符 加 // 用自己计算 先算右侧结果 在赋值给左侧变量 int i 1; i i 2; …...

BM43-包含min函数的栈
题目 定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的 min 函数,输入操作时保证 pop、top 和 min 函数操作时,栈中一定有元素。 此栈包含的方法有: push(value):将value压入栈中pop():弹出栈顶元素top():获取…...

[学习笔记] [机器学习] 3. KNN( K-近邻算法)及练习案例
视频链接数据集下载地址:《3. KNN及练习案例》配套数据集 1. K-近邻算法(KNN)概念 学习目标: 掌握K-近邻算法实现过程知道K-近邻算法的距离公式知道K-近邻算法的超参数 K K K值以及取值问题知道kd树实现搜索的过程应用KNeighborsClassifier实现分类知…...

React Hooks 钩子函数错误用法,你还在犯这些错误吗
React Hooks 常见错误 前言 本片文章主要是在写react hooks的时候,遇到的常见错误的写法,和错误。也是一个对只是的巩固和总结。 错误一 上代码:正确写法 function TestReactHooksError() {const [test, setTest] useState(test);useEff…...
)
tpm2-tools源码分析之tpm2_evictcontrol.c(1)
TPM 2.0中的tpm2_evictcontrol命令对应的源文件就是tpm2_evictcontrol.c,该文件位于tpm2-tools/tools/下,一共有339行(版本5.5)。 tpm2_evictcontrol的功能是使一个被加载的密钥持久保存、或者从TPM中移除一个持久密钥。命令描述…...

SpringCloud_OpenFeign服务调用和Resilience4J断路器
文章目录 一、负载均衡概论1、服务器负载均衡2、客户端负载均衡3、客户端负载均衡策略(SpringCloudRibbon)4、客户端负载均衡策略(SpringCloudLoadBalancer) 二、SpringCloudOpenFeign服务调用1、OpenFeign服务调用的使用2、OpenFeign服务调用的日志增强3、OpenFeign服务调用超…...

【C++】switch 语句
目录 1、缘起 2、笔记整理 3、if 和 switch 区别 4、总结 1、缘起 最近(2023-04-29)在 BiliBili 黑马程序员学习 C 编程语言,今天学习到了 switch 语句。以前在学习 C 语言 的时候,对这块知识点掌握的不是很好,…...

【Database-06】Centos 9 安装docker版的Oceanbase
1、安装docker 1.1、卸载旧版本 旧版本的 Docker 被称为docker或docker-engine。如果安装了这些,卸载它们以及相关的依赖项。 yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotat…...

TiDB Operator 和 Operator Dashboard
TiDB Operator 和 Operator Dashboard V1TiDB Operator概念实现 Operator Dashboard概念实现 V2思路实例代码TiDB ARM OperatorTiDB ARM Operator Dashboard V1 为了演示如何编写 TiDB Operator 和 Operator Dashboard,我们将分别介绍它们的概念和实现。 TiDB Ope…...
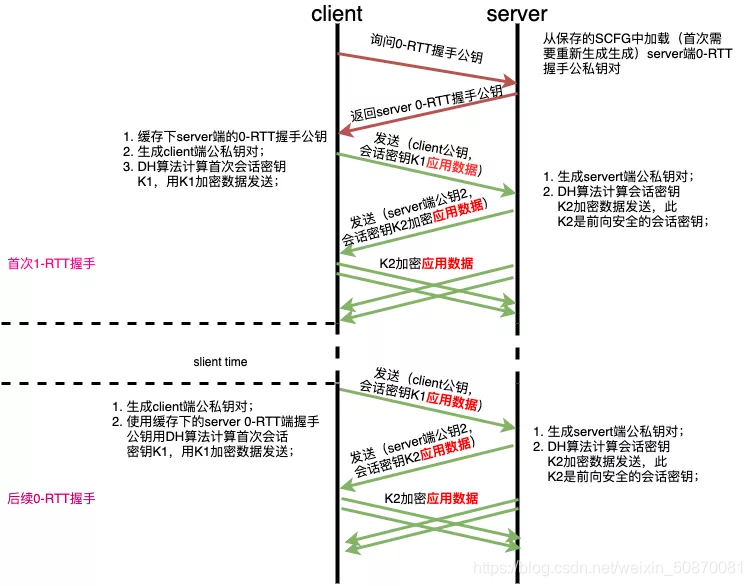
计算机网络闲谈01——QUIC协议
计算机网络闲谈01——QUIC协议 预备知识 重传机制 RTT 一个连接的往返时间 RTO 重传超时时间 RTT和RTO 的关系是:由于网络波动的不确定性,每个RTT都是动态变化的,所以RTO也应随着RTT动态变化。 流量控制 对发送方发送速率的控制 称之为…...

楼层滚动效果(超级简单,易懂)
系列文章目录 文章目录 系列文章目录一、楼层滚动效果图如下1. 下图是纯Css实现的楼层滚动2.通过Js优化后的楼层滚动如下图(🌹🌹) 二、楼层滚动(Css实现)1.滚动原理2.代码如下 三、楼层滚动(JsCss优化后的楼层滚动&…...
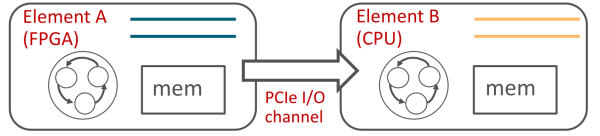
FPGA、 CPU、GPU、ASIC区别
一、为什么使用 FPGA? 众所周知,通用处理器(CPU)的摩尔定律已入暮年,而机器学习和 Web 服务的规模却在指数级增长。 人们使用定制硬件来加速常见的计算任务,然而日新月异的行业又要求这些定制的硬件可被重新…...

ChatGPT 之父承认 GPT-5 并不存在,为什么 OpenAI 总是这么实诚?|万字详述
ChatGPT 诞生前传 来源: 爱范儿 微信号:ifanr 最近,OpenAI 的 CEO Sam Altman 在一场公开会议上为 GPT-5 辟谣。 他声称 OpenAI 并没有在训练 GPT-5,而是一直基于 GPT-4 做别的工作。 OpenAI 是一家非常有趣的机构,和微软、Go…...
华为交换机配置telnet登录图文教程
一、配置交换机管理vlan和地址,配置交换机接口 1.关闭多余的信息提示: [Huawei]undo in en Info: Information center is disabled. [Huawei] 2.交换机配置 在工作中通过Telnet方式登录交换机进行设备登录管理能更加便利,不需要到机房里…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...
