Python 一元线性回归模型预测实验完整版
一元线性回归预测模型
实验目的
通过一元线性回归预测模型,掌握预测模型的建立和应用方法,了解线性回归模型的基本原理
实验内容
一元线性回归预测模型
实验步骤和过程
(1)第一步:学习一元线性回归预测模型相关知识。
线性回归模型属于经典的统计学模型,该模型的应用场景是根据已 知的变量(自变量)来预测某个连续的数值变量(因变量)。例如,餐 厅根据每天的营业数据(包括菜谱价格、就餐人数、预定人数、特价菜 折扣等)预测就餐规模或营业额;网站根据访问的历史数据(包括新用 户的注册量、老用户的活跃度、网页内容的更新频率等)预测用户的支 付转化率;医院根据患者的病历数据(如体检指标、药物服用情况、平 时的饮食习惯等)预测某种疾病发生的概率。
站在数据挖掘的角度看待线性回归模型,它属于一种有监督的学习 算法,即在建模过程中必须同时具备自变量x和因变量y。
相关性分析

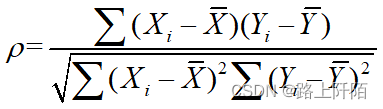

一元线性回归模型
一元线性回归模型也被称为简单线性回归模型,是指模型中只含有一个自变量和一个因变量,用来建模的数据集可以表示成{(x1,y1),(x2,y2),……,(xn,yn)}。其中,xi表示自变量x的第i个值,yi表示因变量y的第i个值,n表示数据集的样本量。当模型构建好之后,就可以根据其他自变量x的值,预测因变量y的值,该模型的数学公式可以表示成:
y=a+bx+ε
其中,
a为模型的截距项,
b为模型的斜率项,
ε为模型的误差项。
模型中的a和b统称为回归系数,误差项ε的存在主要是为了平衡等号两边的值,通常被称为模型无法解释的部分。
拟合线的求解
接下来要学会如何根据自变量x和因变量y,求解回归系数a和b。前面已经提到,误差项ε是为了平衡等号两边的值,如果拟合线能够精确地捕捉到每一个点(所有的散点全部落在拟合线上),那么对应的误差项ε应该为0。按照这个思路来看,要想得到理想的拟合线,就必须使误差项ε达到最小。由于误差项是y与a+bx的差,结果可能为正值或负值,因此误差项ε达到最小的问题需转换为误差平方和最小的问题(最小二乘法的思路)。误差平方和的公式可以表示为
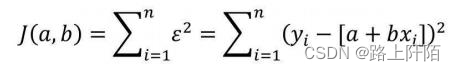
由于建模时的自变量值和因变量值都是已知的,因此求解误差平方和最小值的问题就是求解函数J(a,b)的最小值,而该函数的参数就是回归系数a和b。
该目标函数其实就是一个二元二次函数,如需使得目标函数J(a,b)达到最小,可以使用偏导数的方法求解出参数a和b,进而得到目标函数的最小值。关于目标函数的求导过程如下:





(2)第二步:数据准备,数据来源于课本例题。

序号 x1 年份 水路货运量y
1 1991 1659
2 1992 1989
3 1993 2195
4 1994 2255
5 1995 2329
6 1996 2375
7 1997 2364
8 1998 2354
9 1999 2418
10 2000 2534
11 2001 2568
12 2002 2835
(3)第三步:使用 Python 编写实验代码并做图。
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
# 读取Excel文件
data = pd.read_excel('E:\\File\\class\\数据挖掘\\test1.xlsx')
x = data[['年份']]
y = data['水路货运量y']
# 训练模型
model = LinearRegression()
model.fit(x, y)
# 预测值
x_new = [[2004]]
y_pred = model.predict(x_new)
print("预测值为:", y_pred[0])
# 绘制图像
plt.scatter(x, y)
plt.plot(x, model.predict(x), color='r')
plt.xlabel('年份')
plt.ylabel('水路货运量y')
plt.title('一元线性回归预测模型案例')
plt.show()代码解释:
导入了 sklearn.linear_model 中的 LinearRegression 类,用于构建线性回归模型;
设置了中文字体为 SimHei;
使用 pandas 读取了名为 test1.xlsx 的 Excel 文件,并将年份列作为自变量 x,将水路货运量列作为因变量 y;
使用 LinearRegression 类构建了一个线性回归模型,并使用 fit() 方法拟合了数据;
定义了一个新的自变量 x_new,它的值为 [[2004]],即预测年份为2004;
使用 predict() 方法预测了 x_new 对应的因变量 y_pred;
输出预测值 y_pred;
使用 matplotlib.pyplot 绘制了数据的散点图和线性回归模型的拟合曲线;
添加了坐标轴标签和标题,并显示了图像。
在上面的代码中,首先使用pd.read_excel()函数读取名为"test1.xlsx"的Excel文件,并将其转化为DataFrame格式的数据存储在data变量中。然后,从data中选择了"x"列和"y"列的数据,并将其转化为numpy数组的形式,分别存储在x和y变量中。接着,使用sklearn中的LinearRegression模型进行训练,得到训练好的模型。然后,构造了一个新的自变量x_new,使用训练好的模型进行预测,得到预测值y_pred。最后,使用matplotlib库绘制了数据散点图和拟合直线图,并添加了x轴标签、y轴标签和图像标题,以便进行可视化分析。
需要注意的是,在使用pd.read_excel()函数读取Excel文件时,需要将文件名和路径指定为正确的文件名和路径。如果Excel文件中有缺失值或格式不规范的数据,需要进行数据清洗和预处理,以保证模型的准确性。
(4)第四步:实验结果。
绘图和预测2004年的水路货运量。


这里的预测结果为:2884.0792540792318
相关文章:

Python 一元线性回归模型预测实验完整版
一元线性回归预测模型 实验目的 通过一元线性回归预测模型,掌握预测模型的建立和应用方法,了解线性回归模型的基本原理 实验内容 一元线性回归预测模型 实验步骤和过程 (1)第一步:学习一元线性回归预测模型相关知识。 线性回归模型属于…...

GStreamer第一阶段的简单总结
这里写目录标题 前言个人的总结v4l2src插件的简单使用 前言 因为涉及很多细节的GStreamer官方论坛有详细解链接: GStreamer官网,这里不做说明,以下只是涉及到个人的理解和认知,方便后续的查阅。 个人的总结 1)了解pipeline的使用࿰…...

【网络进阶】服务器模型Reactor与Proactor
文章目录 1. Reactor模型2. Proactor模型3. 同步IO模拟Proactor模型 在高并发编程和网络连接的消息处理中,通常可分为两个阶段:等待消息就绪和消息处理。当使用默认的阻塞套接字时(例如每个线程专门处理一个连接),这两…...

使用div替代<frameset><frame>的问题以及解决办法
首先是原版三层框架的html: <html> <head> <title>THPWP</title> </head> <!-- 切记frameset不能写在body里面,以下代表首页由三层模块组成,其中第一层我是用来放菜单高度占比14%,中间的用作主…...

Verilog中的`define与`if的使用
一部分代码可能有时候用,有时候不用,为了避免全部编译占用资源,可以使用条件编译语句。 语法 // Style #1: Only single ifdef ifdef <FLAG>// Statements endif// Style #2: ifdef with else part ifdef <FLAG>// Statements …...

沃尔玛、亚马逊影响listing的转化率4大因素,测评补单自养号解析
1、listing的相关性:前期我们在找词,收集词的时候,我们通过插件来协助我们去筛选词。我们把流量高,中,低的关键词都一一收集,然后我们再进行对收集得来的关键词进行分析,再进行挑词,…...

静态分析和动态分析
在开发早期,发现并修复bug在许多方面都有好处。它可以减少开发时间,降低成本,并且防止数据泄露或其他安全漏洞。特别是对于DevOps,尽早持续地将测试纳入SDLC软件开发生命周期是非常有帮助的。 这就是动态和静态分析测试的用武之地…...

代码随想录_贪心_leetcode 1005 134
leetcode 1005. K 次取反后最大化的数组和 1005. K 次取反后最大化的数组和 给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组: 选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。 重复这个过程恰好 k 次。可以多次选择同一个下标 i 。 以…...

笔记:对多维torch进行任意维度的多“行”操作
如何取出多维torch指定维度的指定“行” 从二维torch开始新建torch取出某一行取出某一列一次性取出多行取出连续的多行取出不连续的多行 一次取出多列取出连续的多列取出不连续的多列 考虑三维torch取出三维torch的任意两行(means 在dim0上操作)取出连续…...
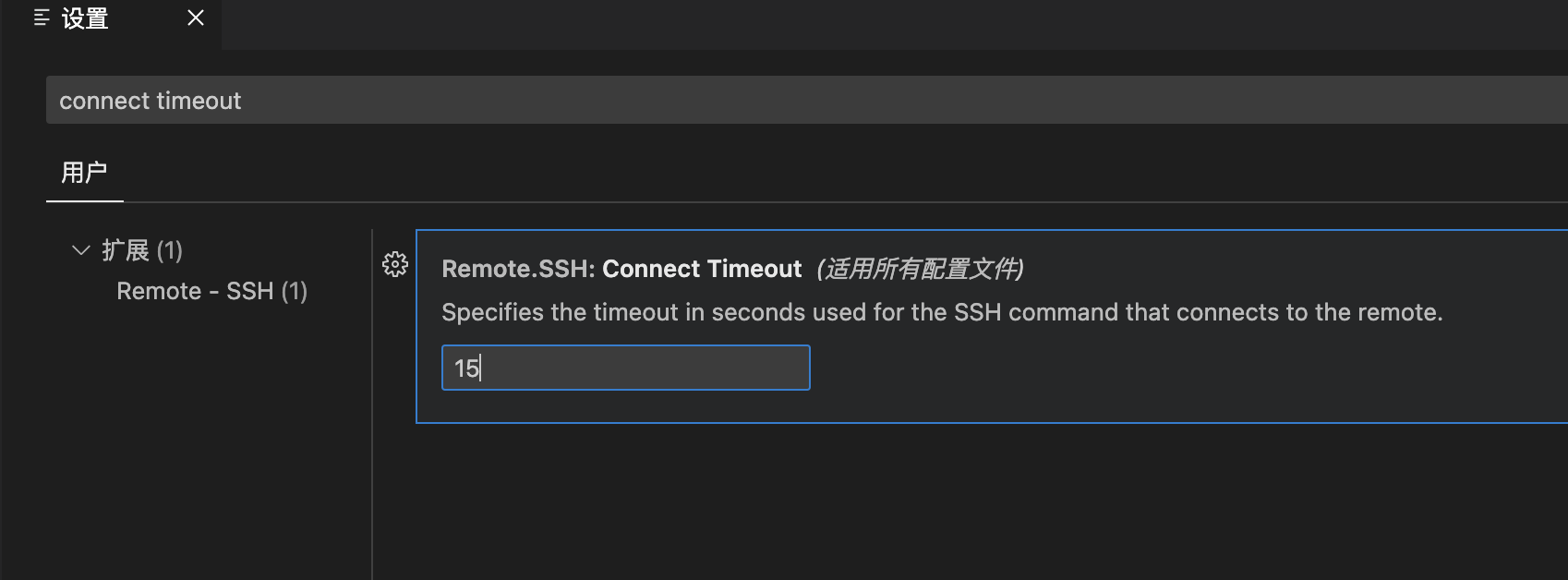
【VSCode】1、VSCode 如何连接服务器
文章目录 一、安装 remote-ssh 插件二、直接连接三、配置 SSH 公匙,免密登录 一、安装 remote-ssh 插件 点击插件搜索框,搜 remote-ssh,点击安装 安装完成后就会出现下面的图标: 二、直接连接 点击加号,输入 ssh 连接…...

AI工具:通过智能实现工作和学习效率的革命化
AI工具是指一系列人工智能技术和工具,包括机器学习、深度学习、自然语言处理、计算机视觉等。这些工具可以帮助开发人员和数据科学家通过处理和分析海量数据来自动识别和解决问题,提供智能的决策和预测模型。常见的AI工具包括TensorFlow、PyTorch、Keras…...

static 和构造方法
文章目录 static构造方法内存中数据的存储方式示例 static 具体对象的属性,称之为对象属性,成员属性,实例属性。 具体对象的方法,称之为对象方法,成员方法,实例方法。 静态:static 和具体对…...

【Linux 裸机篇(八)】I.MX6U EPIT 定时器中断、定时器按键消抖
目录 一、EPIT 定时器简介二、定时器按键消抖 一、EPIT 定时器简介 EPIT 的全称是: Enhanced Periodic Interrupt Timer,直译过来就是增强的周期中断定时器,它主要是完成周期性中断定时的。学过 STM32 的话应该知道, STM32 里面的…...

Web安全 XSS靶场搭建(玩转整个XSS环境.)
Web安全 XSS靶场搭建 XSS又叫CSS(Cross Site Script)跨站脚本攻击,指的是攻击者在Web页面,插入恶意JS代码,当用户浏览该页之时,嵌入其中JS代码就会被执行,从而达到攻击的目的.(包含…...
)
前端开发技术——DOM(上)
一.单选题(共4题,44.4分) 1 下列选项中,关于事件的描述错误的是() A、 事件指的是可以被JavaScript侦测到的行为 B、 事件驱动程序指的是事件触发后要执行的代码 C、 事件源是指触发的事件 D、 事件的种类称为事件…...

银河麒麟v10服务器版安装OpenDDS
1. OpenDDS简介 OpenDDS是OMG数据分发服务(DDS)的一种开源实现,它遵循实时系统v1.2的DDS规范(OMG Document formal/07-01-01)和实时公布/订阅互操作性通信协议v2.1的DDS-RTPS规范(OMG Document formal/2010-11-01)。OpenDDS由OCI公司设计和维护,可从http…...

curl方式调用电商API接口示例 详细介绍
cURL是一个利用URL语法在命令行下工作的文件传输工具,1997年首次发行。它支持文件上传和下载,所以是综合传输工具,但按传统,习惯称cURL为下载工具。cURL还包含了用于程序开发的libcurl。 cURL支持的通信协议有FTP、FTPS、HTTP、H…...

Duboo介绍与入门
文章目录 1、Dubbo的前世今生2、Dubbo的快速入门2.1、Dubbo的基本架构2.2、Nacos2.3、管理后台2.4、入门案例2.4.1、服务提供者搭建环境代码实现配置文件 2.4.2、服务消费者搭建环境代码实现配置文件 最后说一句 1、Dubbo的前世今生 2011年10月27日,阿里巴巴开源了…...
人工智能中(Pytorch)框架下模型训练效果的提升方法
大家好,我是微学AI,今天给大家介绍一下人工智能中(Pytorch)框架下模型训练效果的提升方法。随着深度学习技术的快速发展,越来越多的应用场景需要建立复杂的、高精度的深度学习模型。为了实现这些目标,必须采用一系列复杂的技术来提…...
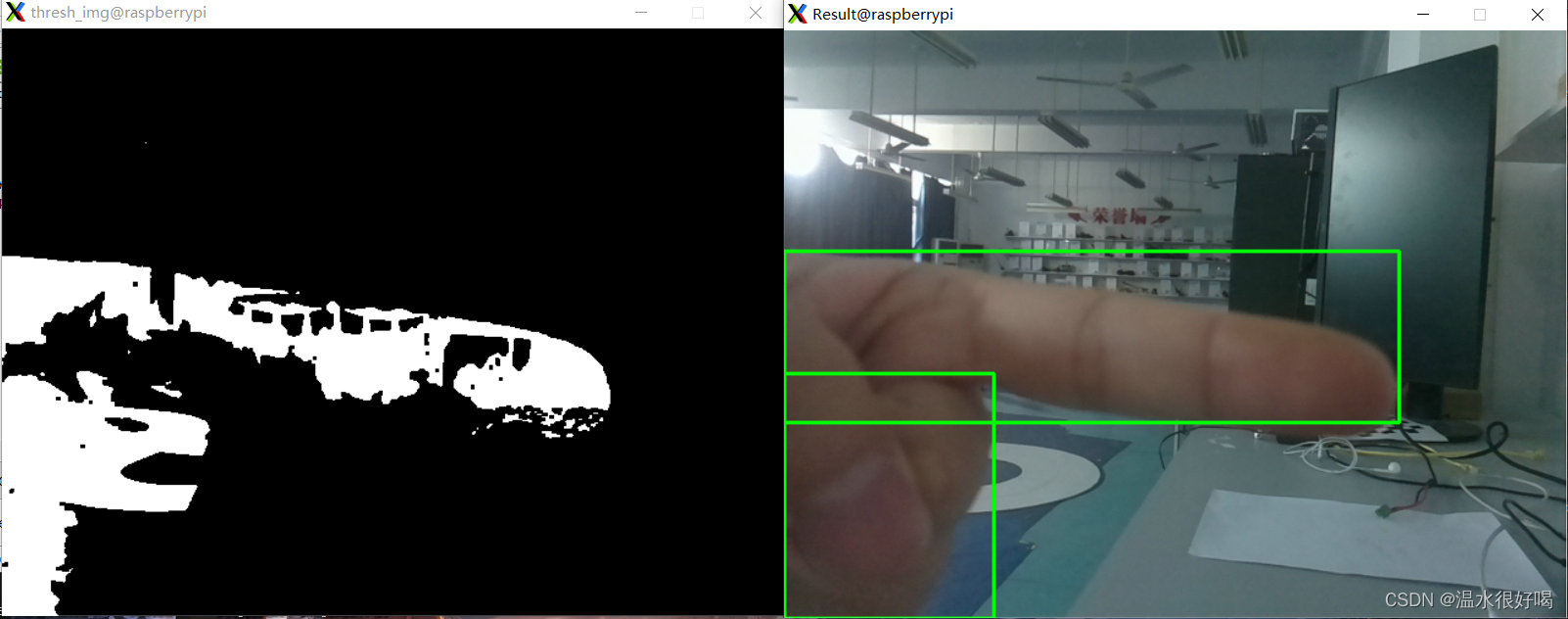
树莓派CSI摄像头使用python调用opencv库函数进行运动检测识别
目录 一、完成摄像头的调用 二、利用python调用opencv库函数对图像进行处理 2.1 图像处理大体流程 2.2 opencv调用函数的参数以及含义 2.2.1 ret, img cap.read() 读取帧图像 2.2.2 cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) 灰度图像 2.2.3 gray_diff_img cv2.absdiff(g…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...
