【学习笔记】CF613E Puzzle Lover
这题本质上还是数据结构。
首先看到这个 2 × n 2\times n 2×n的网格图就很容易想到分治。我们还是考虑把要统计的东西变得可视化,一条路径要么穿过中线一次,那么我们可以将两边的串拼起来得到答案;要么穿过中线两次,考虑其中一边的路径是固定的,那么我们枚举两个端点再判断一下和原串是否匹配的上就做完了。那么考虑预处理出 d p i , j , 0 / 1 , 0 / 1 dp_{i,j,0/1,0/1} dpi,j,0/1,0/1表示从位置 ( 1 / 2 , i ) (1/2,i) (1/2,i)开始,匹配长度为 j j j,向左/右走的方案数,这事实上非常好转移,可以自己编一下。当然可能还要把串正着和倒着处理一边,总之挺麻烦的。
将网格图翻转后做两次即可得到答案。求 L c p Lcp Lcp可以用暴力 d p dp dp代替。事实上也并不需要分治。注意不要算重。
细节题,贼容易写挂。
复杂度 O ( n 2 ) O(n^2) O(n2)。
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define inf 0x3f3f3f3f
#define db double
#define cpx complex<db>
using namespace std;
const int mod=1e9+7;
const int N=2005;
int n,K,Right[2][N][N],Left[2][N][N],dpl[2][N][N],res;
string s[2],str;
void add(int &x,int y){x=(x+y)%mod;
}
void solve(){for(int i=0;i<2;i++){for(int j=n-1;j>=0;j--){for(int k=0;k<K;k++){Right[i][j][k]=(s[i][j]!=str[k])?0:((j!=n-1&&k>=1)?(Right[i][j+1][k-1]+1):1);}}}for(int i=0;i<2;i++){for(int j=0;j<n;j++){for(int k=0;k<K;k++){Left[i][j][k]=(s[i][j]!=str[k])?0:((j>=1&&k>=1)?(Left[i][j-1][k-1]+1):1);}}}memset(dpl,0,sizeof dpl);for(int i=0;i<2;i++){for(int j=0;j<n;j++){if(s[i][j]==str[0]){dpl[i][j][0]=1;}}}//fixedfor(int i=0;i<n;i++){for(int j=i;j<n;j++){for(int k=0;k<2;k++){//strangeif(Left[k][j][2*(j-i+1)-1]>=j-i+1&&Right[k^1][i][j-i]>=j-i+1){add(dpl[k][j][2*(j-i+1)-1],1);}}}}for(int k=1;k<K;k++){for(int i=0;i<2;i++){for(int j=0;j<n;j++){if(s[i][j]==str[k]){if(j)add(dpl[i][j][k],dpl[i][j-1][k-1]);if(s[i^1][j]==str[k-1]){if(j&&k-2>=0)add(dpl[i][j][k],dpl[i^1][j-1][k-2]);}}}}}
}
void getans(){//fixedfor(int i=0;i<2;i++){for(int j=0;j<n;j++){add(res,dpl[i][j][K-1]);}}for(int i=1;i<n;i++){for(int j=i+1;j<n;j++){for(int k=0;k<2;k++){if(Right[k][i][K-1]>=j-i+1&&K-(j-i+2)>=0&&Left[k^1][j][K-(j-i+2)]>=j-i+1&&K-2*(j-i+1)-1>=0){add(res,dpl[k^1][i-1][K-2*(j-i+1)-1]);}}}}
}
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>s[0]>>s[1]>>str,n=s[0].size(),K=str.size();//fixedif(K==1){for(int i=0;i<2;i++){for(int j=0;j<n;j++){if(s[i][j]==str[0]){add(res,1);}}}cout<<res;return 0;}if(K==2){for(int i=0;i<2;i++){for(int j=0;j<n-1;j++){if(s[i][j]==str[0]&&s[i][j+1]==str[1]){add(res,1);}if(s[i][j+1]==str[0]&&s[i][j]==str[1]){add(res,1);}}}for(int i=0;i<2;i++){for(int j=0;j<n;j++){if(s[i][j]==str[0]&&s[i^1][j]==str[1]){add(res,1);}}}cout<<res;return 0;}//fixedsolve();getans();//fixedswap(s[0],s[1]),reverse(s[0].begin(),s[0].end()),reverse(s[1].begin(),s[1].end());solve();getans();cout<<res<<"\n";
}
相关文章:

【学习笔记】CF613E Puzzle Lover
这题本质上还是数据结构。 首先看到这个 2 n 2\times n 2n的网格图就很容易想到分治。我们还是考虑把要统计的东西变得可视化,一条路径要么穿过中线一次,那么我们可以将两边的串拼起来得到答案;要么穿过中线两次,考虑其中一边的…...

软考报名资格审核要多久?证明材料要哪些?
软考报名资格审核要多久? 一般来说,软考资格审核时间不超过1个工作日。当然,每个地区的具体情况都不一样。有些地区估计需要1-3个工作日。总之,为了顺利成功报名,大家应尽快报名,不要拖到最后一天。 软考…...

2023-04-27 polardbx-LSM-tree的Parallel Recovery性能优化
背景 数据库的Crash Recovery时长关系到数据库的可用性SLA、故障止损时间、升级效率等多个方面。本文描述了针对X-Engine数据库存储引擎的一种Crash Recovery优化手段,在典型场景下可以显著缩短数据库实例的故障恢复时间,提升用户使用感受。 当前面临的问题 X-Engine是阿里…...

创作纪念日让 AI 与我共同记录下今天 — 【第五周年、1460天】
今天正是五一,收到一条消息? 五一还要我加班 😏? 喔,原来是 CSDN 给我发的消息呀!我在 CSDN 不知不觉已经开启第五周年啦! 目录 1.机缘2.收获3.日常4.我与 AI 的“合作”part Ipart II Super al…...

枚举法计算24点游戏
# 请在此处编写代码 # 24点游戏 import itertools# 计算24点游戏代码 def twentyfour(cards):"""(1)itertools.permutations(可迭代对象):通俗地讲,就是返回可迭代对象的所有数学全排列方式。itertools.permutations("1118") -…...

@Cacheable注解
Cacheable注解是Spring框架中提供的一种缓存技术, 用于标记一个方法的返回值可以被缓存起来,当再次调用该方法时,如果缓存中已经存在缓存的结果,则直接从缓存中获取结果而不是再次执行该方法,从而提高系统的性能和响应…...

CentOS分区挂载 fdisk、parted方式解析
1 介绍 在linux中,通常会将持久化数据保存到硬盘当中,但是硬盘一把会比较大,因此我们为了方便管理,会将一个硬盘分成多个逻辑硬盘,称之为分区。 为了能够让分区中的文件使得能让操作系统处理,则需要对分区…...

BuildKit
介绍 BuildKit是一个现代化的构建系统,主要用于构建和打包容器镜像。它是Docker官方的构建引擎,支持构建多阶段构建、缓存管理、并行化构建、多平台构建等功能。BuildKit还支持多种构建语法和格式,包括Dockerfile、BuildKit Build Specifica…...
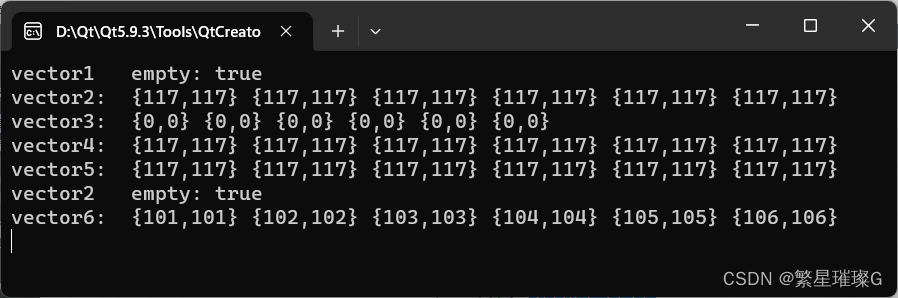
c++ 11标准模板(STL) std::vector (二)
定义于头文件 <vector> template< class T, class Allocator std::allocator<T> > class vector;(1)namespace pmr { template <class T> using vector std::vector<T, std::pmr::polymorphic_allocator<T>>; }(2)(C17…...

Python 循环技巧
目录 在字典中循环时,用 items() 方法可同时取出键和对应的值: 在序列中循环时,用 enumerate() 函数可以同时取出位置索引和对应的值: 同时循环两个或多个序列时,用 zip() 函数可以将其内的元素一一匹配:…...

【Java笔试强训 7】
🎉🎉🎉点进来你就是我的人了博主主页:🙈🙈🙈戳一戳,欢迎大佬指点! 欢迎志同道合的朋友一起加油喔🤺🤺🤺 目录 一、选择题 二、编程题 🔥Fibona…...
工作7年的程序员,明白了如何正确的“卷“
背景 近两年,出台和落地的反垄断法,明确指出要防止资本无序扩张。 这也就导致现在的各大互联网公司,不能再去染指其他已有的传统行业,只能专注自己目前存量的这些业务。或者通过技术创新,开辟出新的行业。 但创新这…...

数学建模——查数据
如果选择C题的小伙伴常常需要查找一些数据,那么这些数据一般都可以从哪里找到呢? 常用的查数据平台 优先在知网、谷歌学术等平台搜索国家统计局 最全面,月度季度年度,各地区各部门各行业,包罗万象 https://data.stat…...

PAT A1019 General Palindromic Number
1019 General Palindromic Number 分数 20 作者 CHEN, Yue 单位 浙江大学 A number that will be the same when it is written forwards or backwards is known as a Palindromic Number. For example, 1234321 is a palindromic number. All single digit numbers are pa…...
ChatGPT会颠覆SEO内容创作吗
近几年 AI 的发展日新月异。除了搜索算法本身大规模应用人工智能,我也一直关注着 AI 用于写作的进展。 上篇关于 Google 有用内容更新的帖子还在说,高质量内容创作是 SEO 最难的事之一,对某些网站来说,如果能有工具帮助ÿ…...
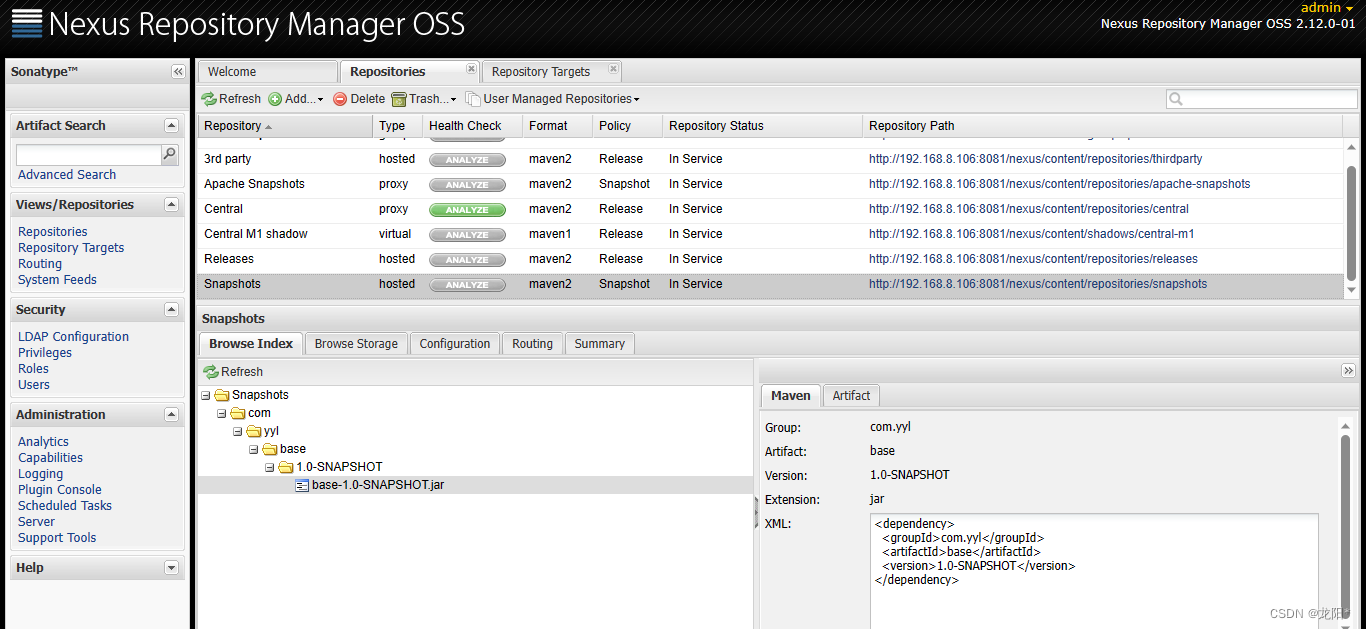
Maven私服搭建
为什么要搭建私服 通常在maven项目的pom.xml文件中引入了某个依赖包之后,maven首先会去本地仓库去搜索,本地仓库搜索不到会去maven的配置文件settings.xml中配置的maven镜像地址去找,比如: <mirrors><!-- mirror| Specif…...
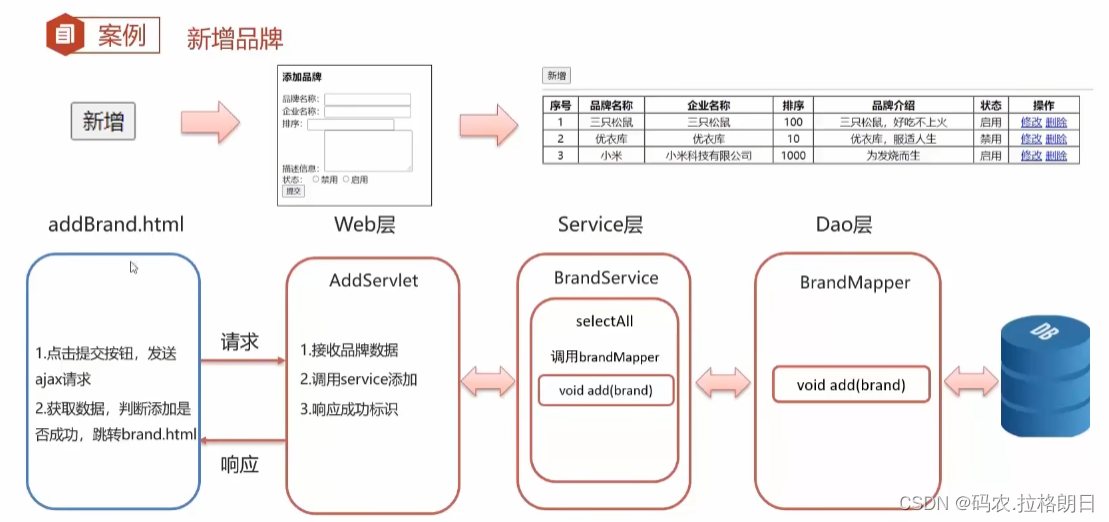
Ajax和Json综合案例
1. 查询所有 创建brand.html,使用axios发送请求,其中查询一般采用get的请求方式 <script src"js/axios-0.18.0.js"></script><script>//1. 当页面加载完成后,发送ajax请求window.onload function () {//2. 发送ajax请求axi…...

【genius_platform软件平台开发】第九十四讲:int64_t的格式化问题(lld和PRId64)
问题起因是在进行上位机软件优化的工作安排时,同事对unsigned long long 类型的时间戳进行了格式化输出优化,从%ull优化为了% PRIu64,我进行代码合并请求处理的时候突然感觉这个可以仔细查一下。查阅到的相关资料如下: * 1. int6…...

多模态之clip
论文:Learning Transferable Visual Models From Natural Language Supervision Github:https://github.com/OpenAI/CLIP OpenAI出品 论文通过网络爬取4亿(image, text)对,使用对比学习的方法训练得到clip(Contrastive Languag…...
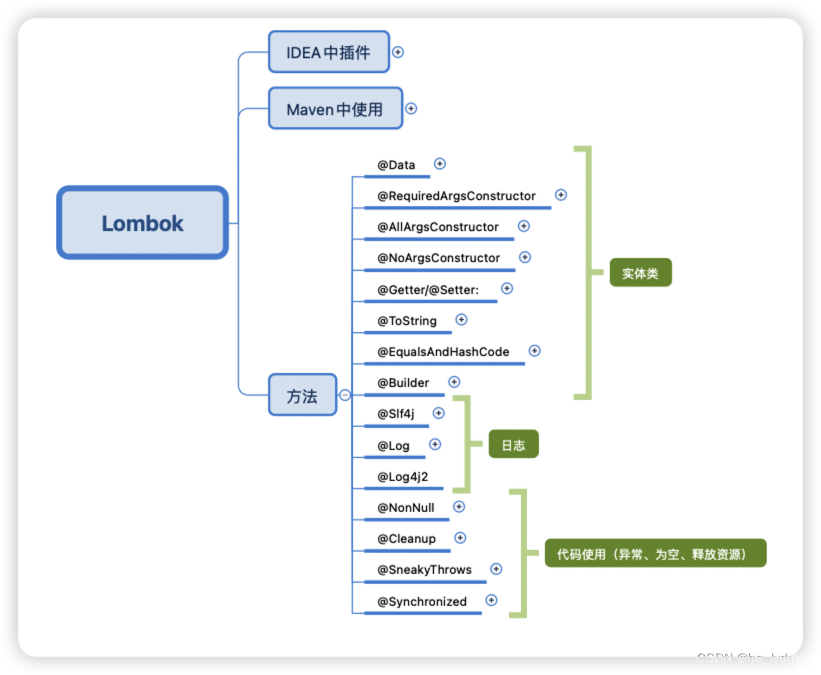
Lombok常用注解
文章目录 一、简介二、Idea中配置三、Maven中配置四、相应注解1、Data2、RequiredArgsConstructor3、AllArgsConstructor4、NoArgsConstructor5、Getter/Setter:6、ToString7、EqualsAndHashCode8、Builder9、NonNull10、Log11、Slf4j12、Log4j213、SneakyThrows14、Cleanup15、…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...
