机器学习实战:Python基于DT决策树模型进行分类预测(六)
文章目录
- 1 前言
- 1.1 决策树的介绍
- 1.2 决策树的应用
- 2 Scikit-learn数据集演示
- 2.1 导入函数
- 2.2 导入数据
- 2.3 建模
- 2.4 评估模型
- 2.5 可视化决策树
- 2.6 优化模型
- 2.7 可视化优化模型
- 3 讨论
1 前言
1.1 决策树的介绍
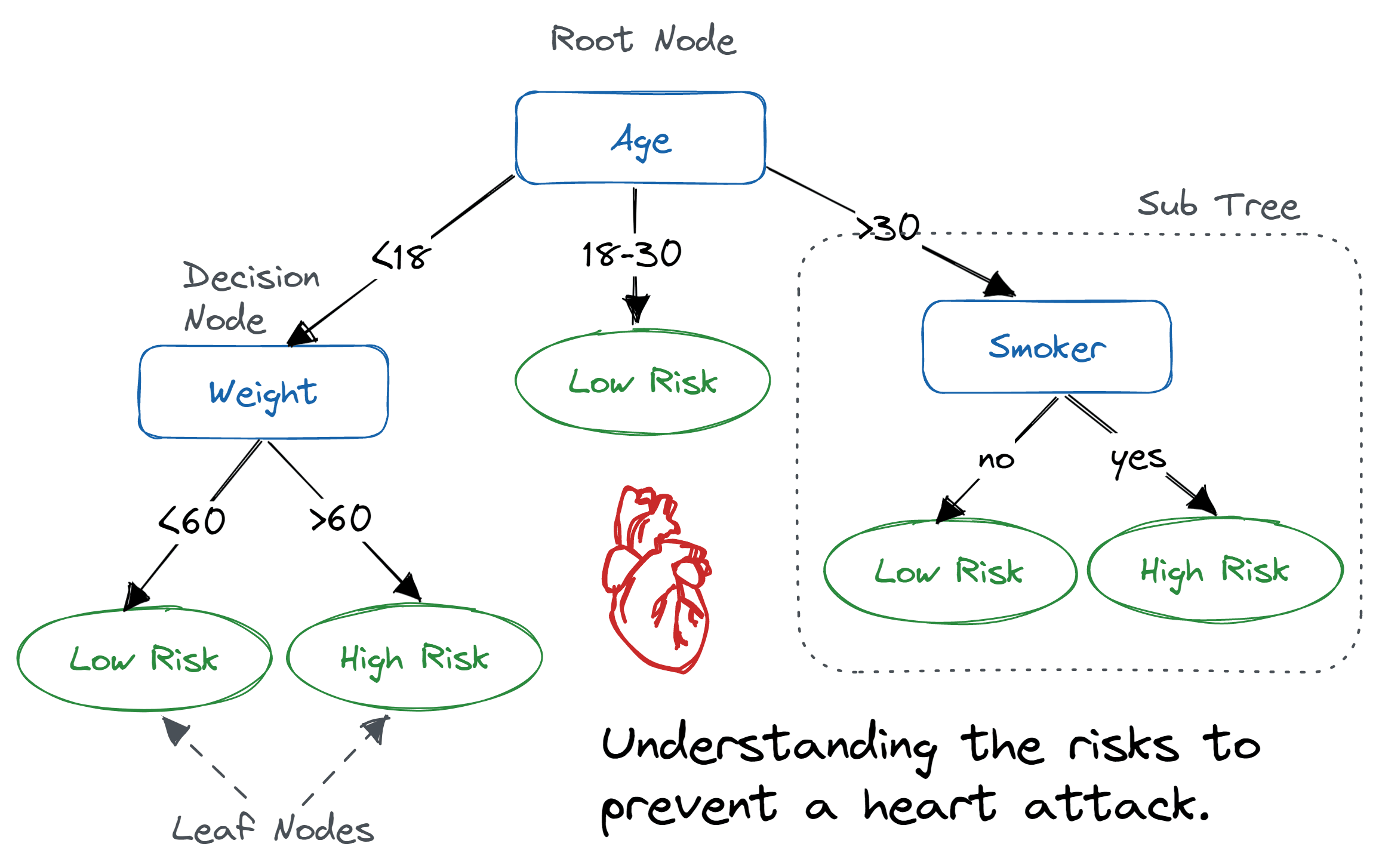
决策树(Decision Tree,DT)是一种类似流程图的树形结构,其中内部节点表示特征或属性,分支表示决策规则,每个叶节点表示结果。在决策树中,最上方的节点称为根节点。它学习基于属性值进行分区。它以递归方式进行分区,称为递归分区。这种类似流程图的结构有助于决策制定。它的可视化类似于流程图,可以很容易地模拟人类的思维过程。这就是为什么决策树易于理解和解释的原因。
决策树的时间复杂度是给定数据中记录和属性数量的函数。决策树是一种无分布或非参数方法,不依赖于概率分布假设。决策树可以很好地处理高维数据。
其原理可简单分为三步:**选择最优划分属性:**根据信息增益、信息增益比、基尼指数等方法,选择当前数据集中最优的属性作为划分属性,将数据集分成多个子集。**递归生成子树:**对每个子集重复步骤1,递归生成子树,直到所有的叶子节点都属于同一类别。**剪枝:**为了防止过拟合,需要对决策树进行剪枝,即去除一些分支或子树,使决策树更加简洁。
优点:
-
易于理解和解释:DT算法可以生成易于理解和解释的决策树模型,因此非专业人员也可以理解和使用该算法。
-
可解释性和可视化:DT算法可以通过绘制决策树的形式来直观地呈现分类过程,增强了模型的可解释性和可视化性。
-
适用性广泛:DT算法可以处理离散和连续型特征,且对数据的分布和噪声鲁棒性较高。
缺点:
-
容易过拟合:DT算法在训练集上可能表现得很好,但在测试集上表现得很差,容易过拟合。
-
对噪声和异常值比较敏感:DT算法对噪声和异常值比较敏感,容易导致生成的决策树过于复杂。
-
不支持在线学习:DT算法需要一次性加载所有的数据,并在内存中进行操作,因此不支持在线学习。
1.2 决策树的应用
决策树对于常规分类跟前面介绍的五种分类器其实差别不大,不过鉴于其易理解易运用对于实际生活还是有着不少便利。
-
金融风险评估:决策树可以用于预测借款人的还款能力和信用等级,帮助金融机构决定是否批准贷款。
-
医疗诊断:决策树可以用于帮助医生诊断疾病或推荐治疗方案,根据患者的症状和医疗历史进行分类。
-
客户关系管理:决策树可以用于客户细分,根据客户的购买历史、偏好和行为预测客户的需求,帮助企业定制个性化的服务。
-
电子商务:决策树可以用于商品推荐,根据用户的历史购买记录和行为推荐符合用户偏好的商品。
-
生产优化:决策树可以用于优化生产过程,根据生产线上的各种因素,例如温度、湿度、时间等来决定何时停机、何时更换部件,从而减少故障和损失。
-
人力资源管理:决策树可以用于招聘、晋升和培训决策,根据员工的学历、工作经验、业绩等因素,预测员工的发展潜力和能力,从而做出更加科学的决策。
2 Scikit-learn数据集演示
2.1 导入函数
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn import metrics
2.2 导入数据
先下载这个糖尿病数据集:https://www.kaggle.com/datasets/uciml/pima-indians-diabetes-database
注册或者用google登陆一下download即可,若下载失败或者登不上去的可后台回复
0420领取示例数据集
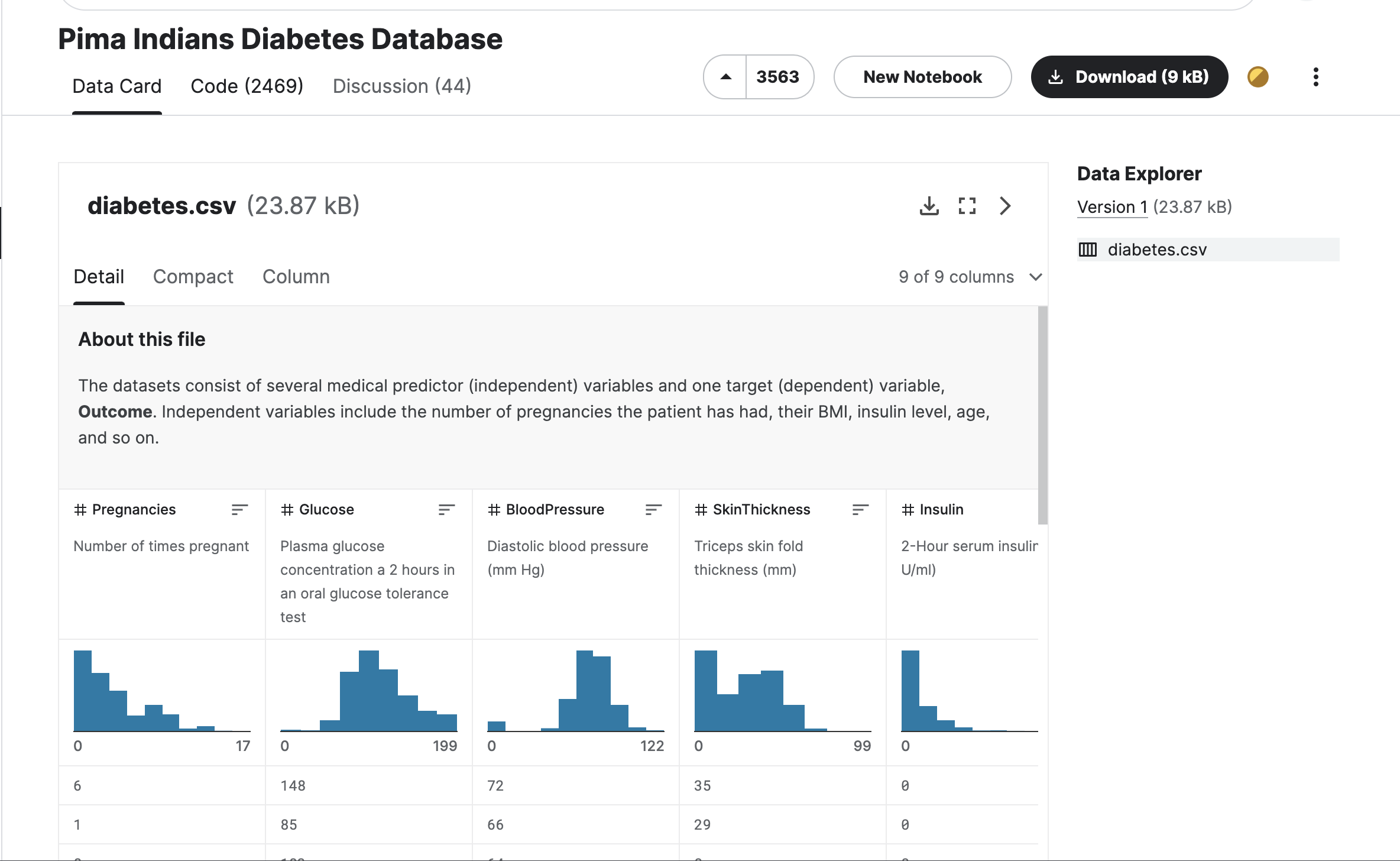
然后导入数据,这里用了小写表头,所以header=None,然后再将首行定义为列名,若参考网上其他教程,留意库和函数的更新更改,否则可能会报错
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
pima = pd.read_csv("diabetes.csv", header=None, names=col_names)
pima = pima.iloc[1:]
pima.head()

2.3 建模
这里定义自变量和因变量,然后分组
feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
X = pima[feature_cols] # Features
y = pima.label # Target variable# 训练集测试集7/3分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)
建立决策树
clf = DecisionTreeClassifier()
clf = clf.fit(X_train,y_train)
y_pred = clf.predict(X_test)2.4 评估模型
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))

结果能达到69.697%,还是可以的
2.5 可视化决策树
这两个包先下载了,且检查路径没问题
#!pip install graphviz
#!pip install pydotplus
可视化
from sklearn.tree import export_graphviz
from six import StringIO
from IPython.display import Image
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data, filled=True, rounded=True,special_characters=True,feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('diabetes.png')
Image(graph.create_png())
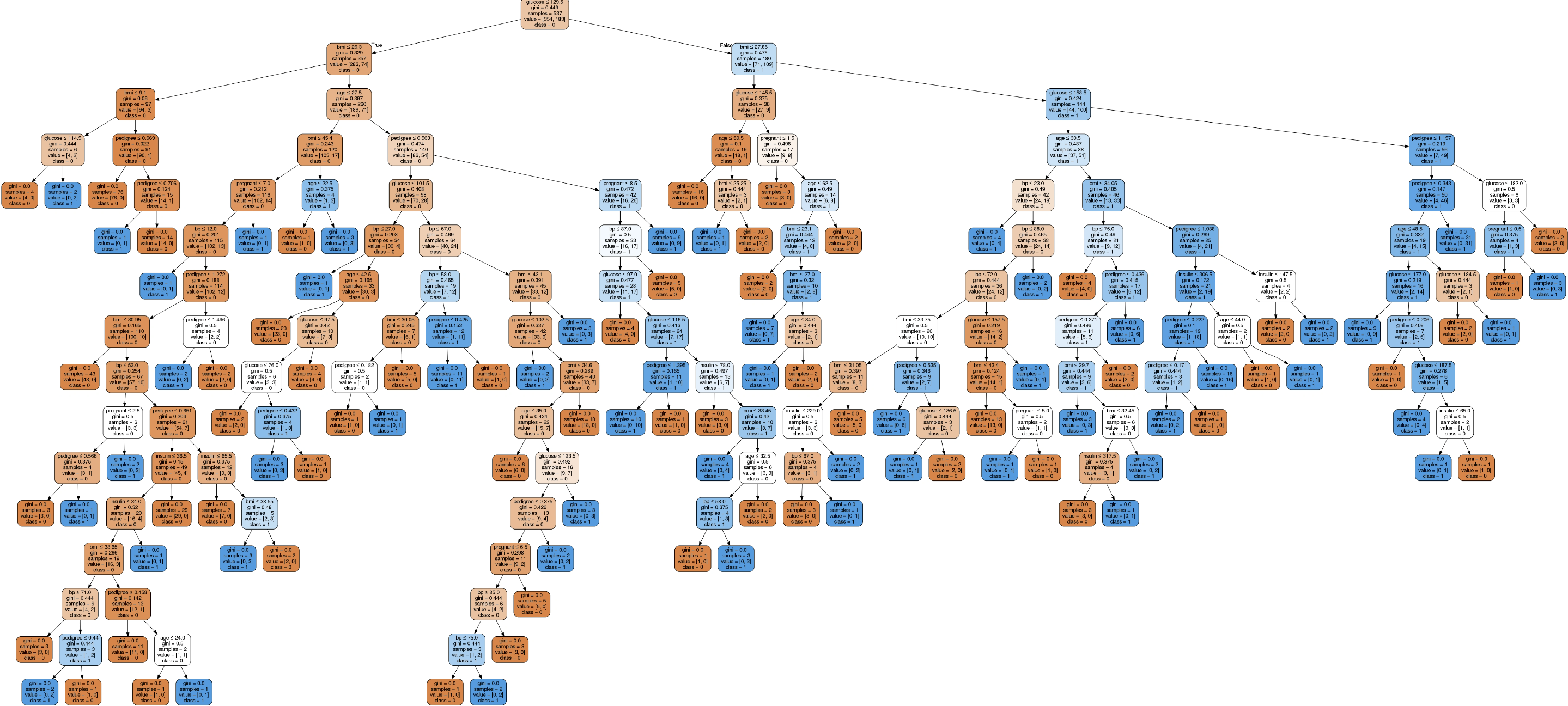
这是原始的分类,每个内部节点都有一个拆分数据的决策规则,称为基尼系数,测量节点的杂质,因此获取更准确的结果需要进行优化。
2.6 优化模型
-
criterion: 可选参数(默认为“gini”)或选择属性选择度量。该参数允许我们使用不同的属性选择度量。支持的标准是“gini”,用于Gini指数,以及“entropy”,用于信息增益。
-
splitter: 字符串,可选参数(默认为“best”)或分割策略。该参数允许我们选择分割策略。支持的策略有“best”选择最佳分割和“random”选择最佳随机分割。
-
max_depth: 整数或None,可选参数(默认为None)或树的最大深度。树的最大深度。如果为None,则节点会扩展直到所有叶子节点包含的样本数少于min_samples_split。最大深度的值过高会导致过拟合,而过低的值会导致欠拟合。
这里选择max_depth=3,也可以换成其他预修剪
clf = DecisionTreeClassifier(criterion="entropy", max_depth=3)
clf = clf.fit(X_train,y_train)
y_pred = clf.predict(X_test)
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))

分类率变成了77.056%,效果可观
2.7 可视化优化模型
from six import StringIO from IPython.display import Image
from sklearn.tree import export_graphviz
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data, filled=True, rounded=True,special_characters=True, feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('diabetes.png')
Image(graph.create_png())
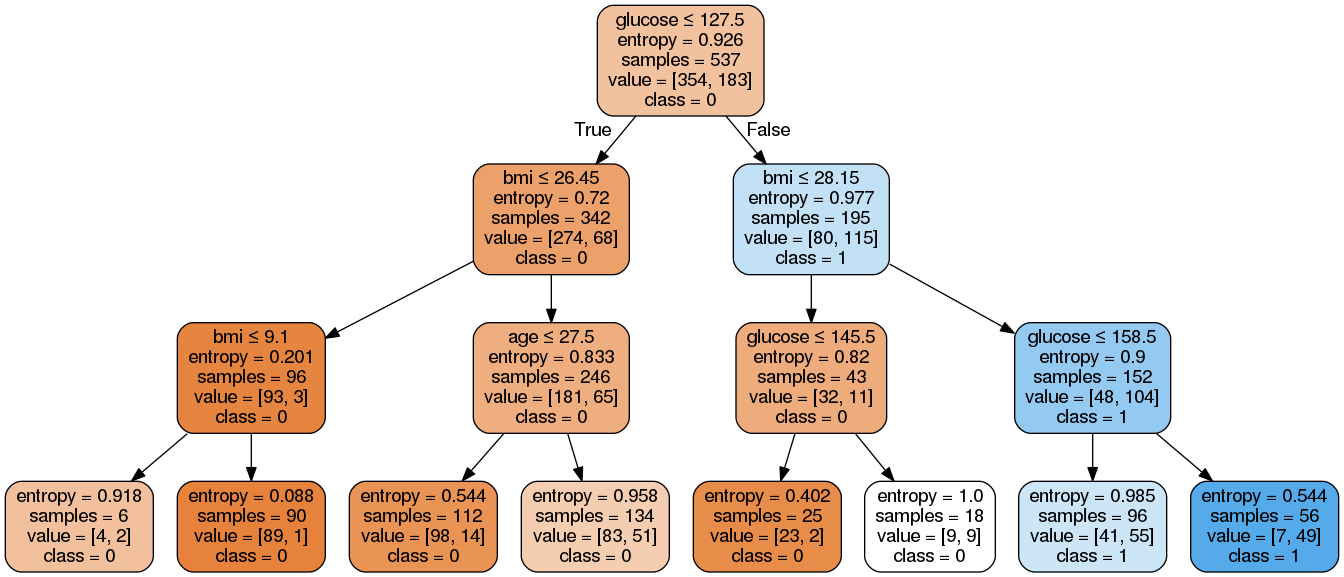
确实结果比优化前的更简洁了,分类后的复杂程度大大降低了。
3 讨论
Python中的决策树是机器学习(数据科学的重要子集)领域非常流行的监督学习算法技术,但是,决策树并不是可用于提取此信息的唯一聚类技术。
它是一种监督式机器学习技术,其中数据根据某个参数连续拆分。决策树分析可以帮助解决分类和回归问题,这里只演示了分类。决策树算法将数据集分解为更小的子集;同时,相关的决策树是逐步开发的。决策树由节点(测试某个属性的值)、边/分支(对应于测试结果并连接到下一个节点或叶)和叶节点(预测结果的终端节点)组成,使其成为一个完整的结构。
相关文章:

机器学习实战:Python基于DT决策树模型进行分类预测(六)
文章目录 1 前言1.1 决策树的介绍1.2 决策树的应用 2 Scikit-learn数据集演示2.1 导入函数2.2 导入数据2.3 建模2.4 评估模型2.5 可视化决策树2.6 优化模型2.7 可视化优化模型 3 讨论 1 前言 1.1 决策树的介绍 决策树(Decision Tree,DT)是一…...
操作系统之进程同异步、互斥
引入 异步性是指,各并发执行的进程以各自独立的、不可预知的速度向前推进。 但是在一定的条件之下,需要进程按照一定的顺序去执行相关进程: 举例说明1: 举例说明2: 读进程和写进程并发地运行,由于并发必然导致异步性…...

你了解这2类神经性皮炎吗?常常预示着这5类疾病!
神经性皮炎属于慢性皮肤病,患者皮肤可出现局限性苔藓样变,同时伴有阵发性瘙痒。神经性皮炎易发生在颈部两侧和四肢伸侧,中年人是高发人群。到目前为止神经性皮炎病因还并不是很明确,不过一部分病人发病前常常出现精神神经方面异常…...
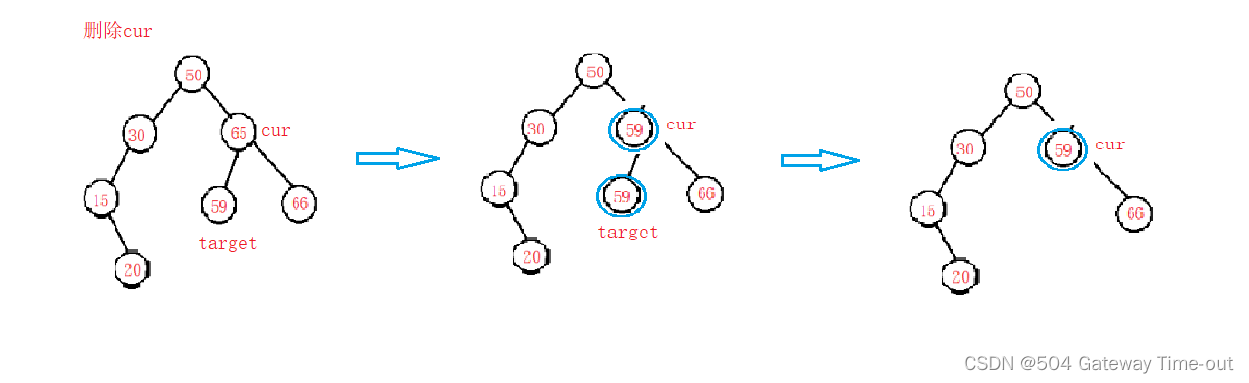
二叉搜索树【Java】
文章目录 二叉搜索树的性质二叉搜索树的操作遍历查找插入删除 二叉搜索树又称为二叉排序树,是一种具有一定性质的特殊的二叉树; 二叉搜索树的性质 若它的左子树不为空,则左子树上结点的值均小于根节点的值; 若它的右子树不为空&a…...

二叉树的遍历方式
文章目录 层序遍历——队列实现分析Java完整代码 先序遍历——中左右分析递归实现非递归实现——栈实现 中序遍历——左中右递归实现非递归实现——栈实现 后续遍历——左右中递归实现非递归实现——栈加标志指针实现 总结 层序遍历——队列实现 给你二叉树的根节点 root &…...
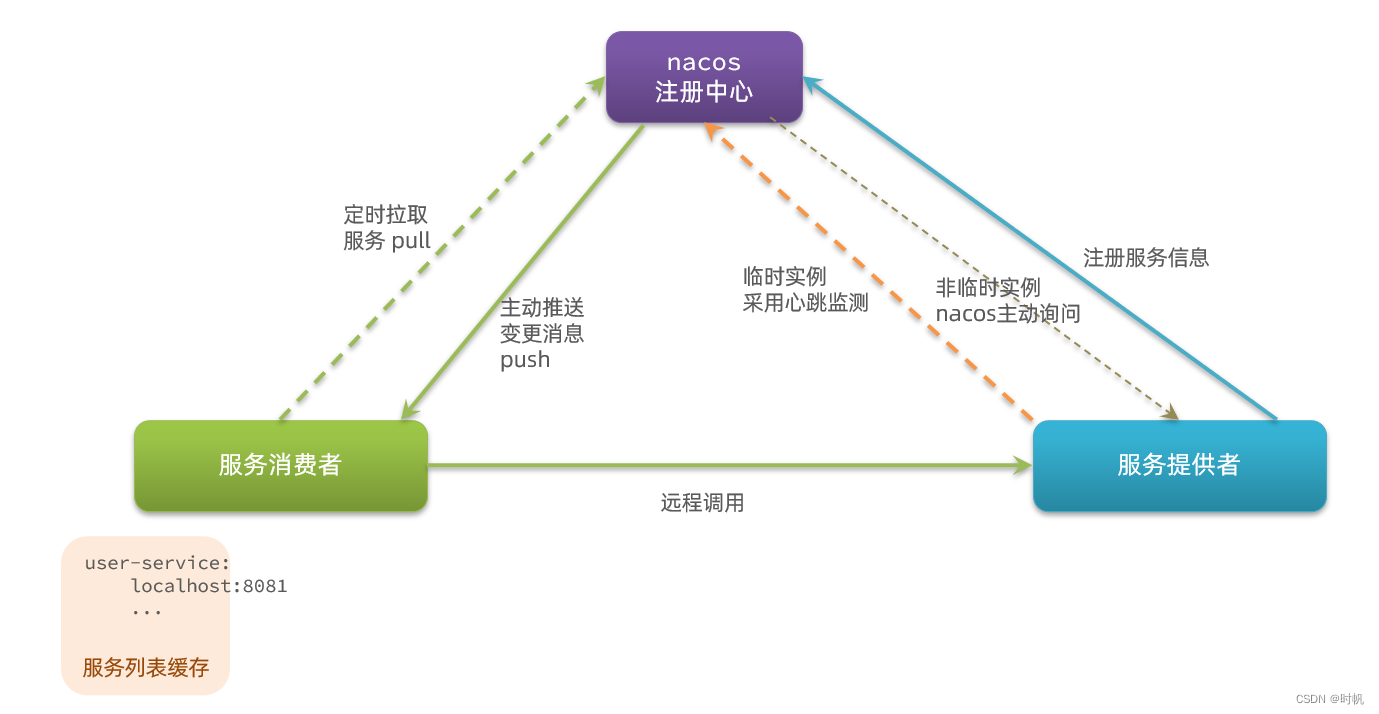
SpringCloud01
SpringCloud01 微服务入门案例 实现步骤 导入数据 实现远程调用 MapperScan("cn.itcast.order.mapper") SpringBootApplication public class OrderApplication {public static void main(String[] args) {SpringApplication.run(OrderApplication.class, args);}…...

SpringBoot整合Redis实现点赞、收藏功能
前言 点赞、收藏功能作为常见的社交功能,是众多Web应用中必不可少的功能之一。而redis作为一个基于内存的高性能key-value存储数据库,可以用来实现这些功能。 本文将介绍如何使用spring boot整合redis实现点赞、收藏功能,并提供前后端页面的…...

【Java入门合集】第一章Java概述
【Java入门合集】第一章Java概述 博主:命运之光 专栏:JAVA入门 学习目标 1.理解JVM、JRE、JDK的概念; 2.掌握Java开发环境的搭建,环境变量的配置; 3.掌握Java程序的编写、编译和运行; 4.学会编写第一个Java程序&#x…...

Android无线调试操作说明
1.首先通过手机机蓝牙将jackpal.androidterm-1.0.70.apk(终端模拟器)传的设备上安装 链接: https://pan.baidu.com/s/151SzEgsX0b_VTWowzfUrsA?pwdrn75 提取码: rn75 复制这段内容后打开百度网盘手机App,操作更方便哦 2.打开这个终端模拟器,输入以下命…...

什么是 Python ?聊一聊Python程序员找工作的六大技巧
最近我一直在思考换工作的事情。因此,这段时间我会看一些题目,看一些与面试相关的内容,以便更好地准备面试。我认为无论你处于什么阶段,面试中都会有技术面试环节。无论是初级职位还是高级职位,都需要通过技术面试来检…...

RabbitMQ 01 概述
什么是消息队列 进行大量的远程调用时,传统的Http方式容易造成阻塞,所以引入了消息队列的概念,即让消息排队,按照队列进行消费。 它能够将发送方发送的信息放入队列中,当新的消息入队时,会通知接收方进行处…...

面经|曹操出行供需策略运营
1.自我介绍 面试官表示看了简历之后,表示对专业能力比较放心。想了解下对于专业能力之外,关于其他方面的介绍。 2.策略运营,除了工具之外,还有哪些能力是需要具备的 回答:主要是从做项目的维度逻辑先去回答的。 分析思…...
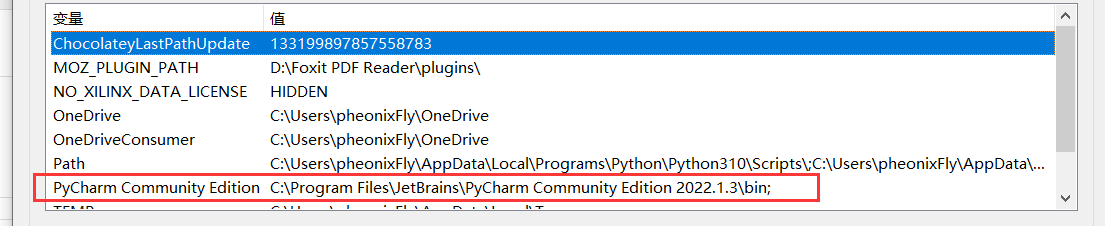
【Python】selenium工具
目录 1. 安装 2. 测试 3. 无头浏览器 4. 元素定位 5. 页面滑动 6. 按键、填写登录表单 7. 页面切换 Selenium是Web的自动化测试工具,为网站自动化测试而开发,Selenium可以直接运行在浏览器上,它支持所有主流的浏览器,可以接…...
实验六~Web事件处理与过滤器
1. 创建一个名为exp06的Web项目,编写、部署、测试一个ServletContext事件监听器。 BookBean代码 package org.example.beans;import java.io.Serializable;/*** Created with IntelliJ IDEA.* Description:* User: Li_yizYa* Date: 2023—04—29* Time: 18:39*/ Su…...
刷题4.28
1、 开闭原则软件实体(模块,类,方法等)应该对扩展开放,对修改关闭,即在设计一个软件系统模块(类,方法)的时候,应该可以在不修改原有的模块(修改关…...

做了一年csgo搬砖项目,还清所有债务:会赚钱的人都在做这件事 !
前段時间,在网上看到一句话:有什么事情,比窮更可怕? 有人回答说:“又忙又窮。” 很扎心,却是绝大多数人的真实写照。 每天拼死拼活的996,你有算过你的時间值多少钱? 我们来算一笔…...
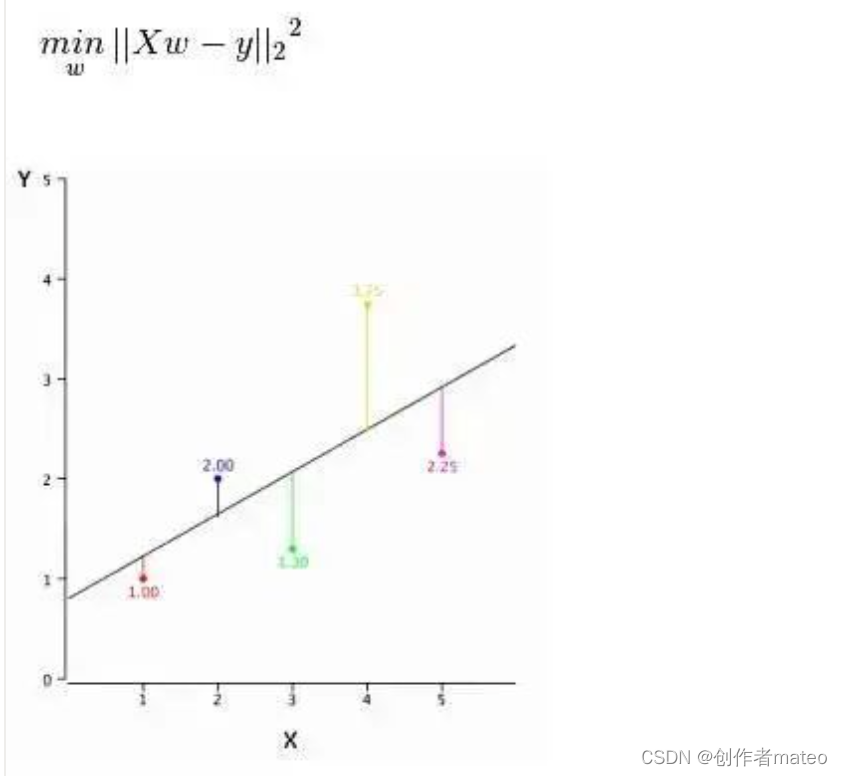
线性回归模型(7大模型)
线性回归模型(7大模型) 线性回归是人工智能领域中最常用的统计学方法之一。在许多不同的应用领域中,线性回归都是非常有用的,例如金融、医疗、社交网络、推荐系统等等。 在机器学习中,线性回归是最基本的模型之一&am…...
 A~D)
VP记录:Codeforces Round 868 (Div. 2) A~D
传送门:CF A题:A-characteristic 构造一个只有 1 , − 1 1,-1 1,−1的数组,满足乘积为 1 1 1的数对的个数为 k k k. 发现 n n n的范围很小,考虑直接暴力枚举数组中 1 1 1的个数,记为 i i i,那么对于1的所有数对来说,我们有 i ∗ ( i − 1 ) / 2 i*(i-1)/2 i∗(i−1)/2个,然后…...

【VQ-VAE-2论文精读】Generating Diverse High-Fidelity Images with VQ-VAE-2
【VQ-VAE-2论文精读】Generating Diverse High-Fidelity Images with VQ-VAE-2 0、前言Abstract1 Introduction2 Background2.1 Vector Quantized Variational AutoEncoder3 Method3.1 Stage 1: Learning Hierarchical Latent Codes3.2 Stage 2: Learning Priors over Latent C…...
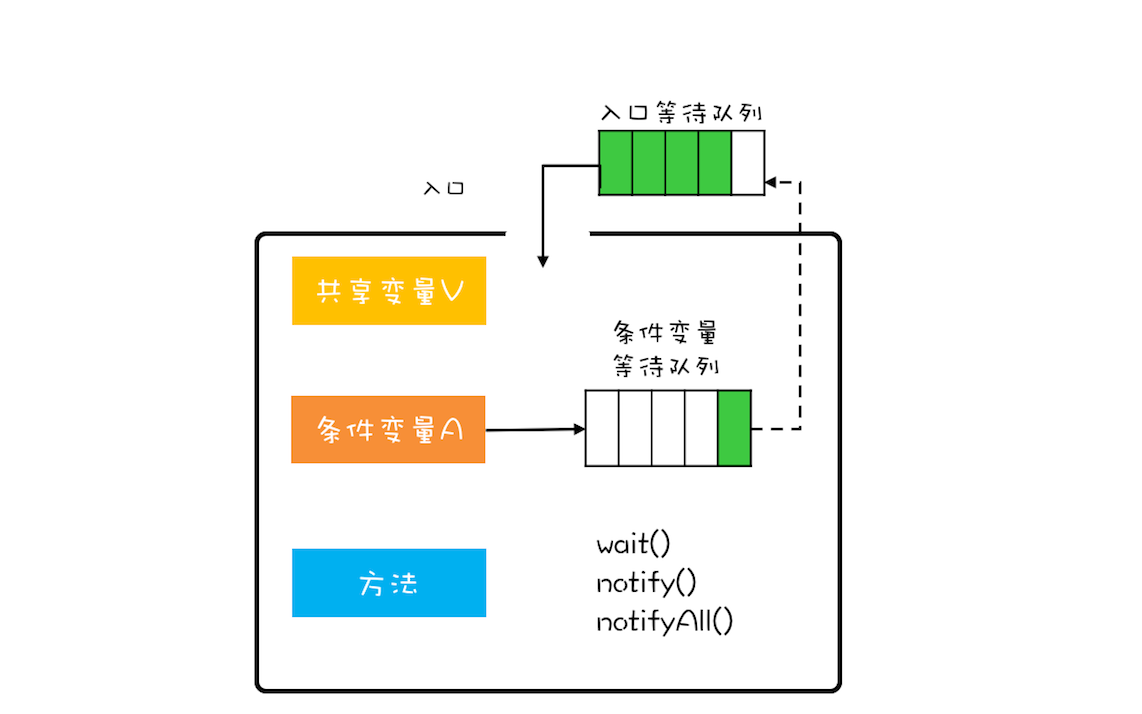
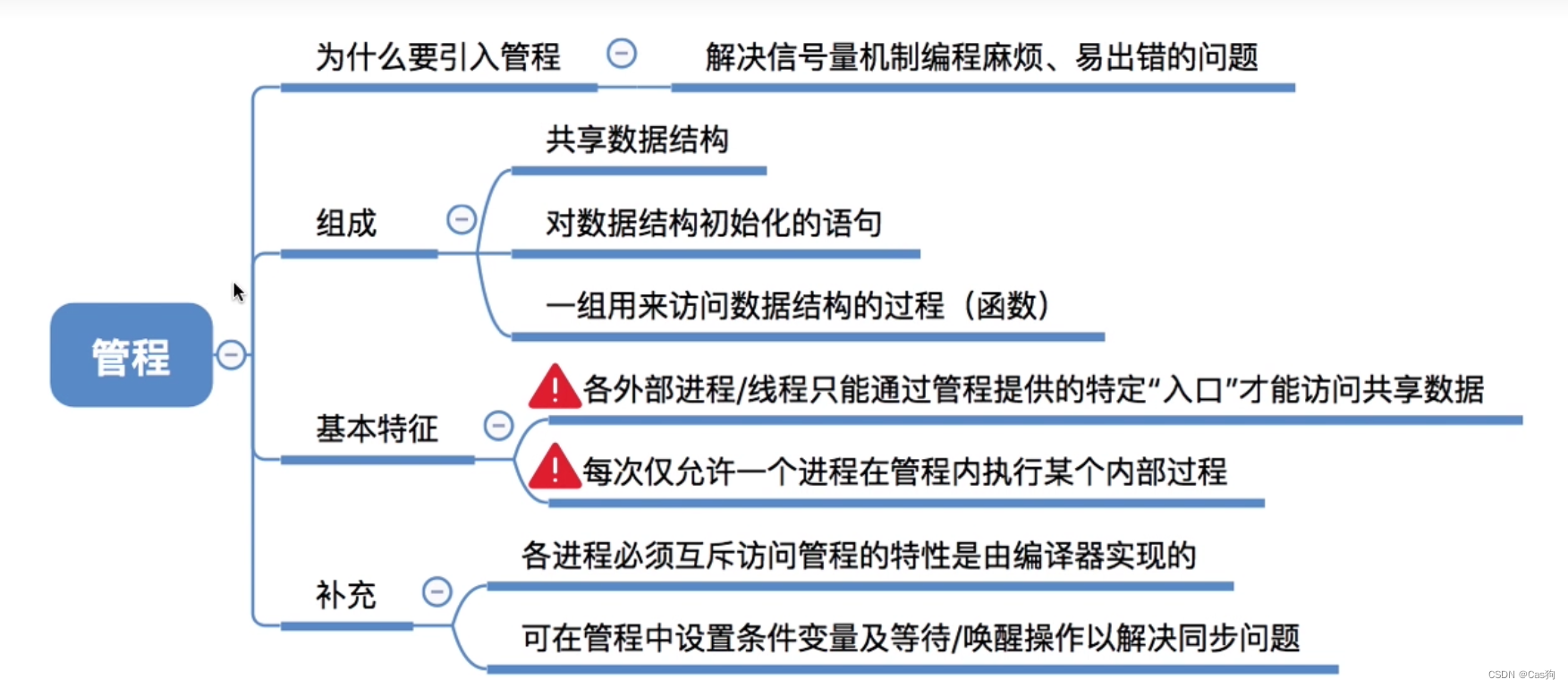
并发编程基石:管程
大家好,我是易安! 如果有人问我学习并发并发编程,最核心的技术点是什么,我一定会告诉他,管程技术。Java语言在1.5之前,提供的唯一的并发原语就是管程,而且1.5之后提供的SDK并发包,也…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
