统计学习方法第四章——朴素贝叶斯法
x.1 前言
朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。是通过给定training dataset学习联合概率分布的方法,是一种生成方法。
x.2 使用贝叶斯定理做分类
使用贝叶斯定理做分类,相比较于朴素贝叶斯即丢除特征条件独立假设这个条件。
假设存在k类 c 1 , c 2 , . . . , c k c_1, c_2, ... , c_k c1,c2,...,ck,给定一个新实例 x = x ( 1 ) , . . . , x ( n ) x=x^{(1)}, ... , x^{(n)} x=x(1),...,x(n),判断该实例来自哪一类。在判断来自哪一类即使用贝叶斯公式计算属于每一个类别的概率 P ( Y = c i ∣ X = x ) = P ( Y = c i ) P ( X = x ∣ Y = c i ) P ( X = x ) P(Y=c_i|X=x)=\frac {P(Y=c_i)P(X=x|Y=c_i)}{P(X=x)} P(Y=ci∣X=x)=P(X=x)P(Y=ci)P(X=x∣Y=ci),分母可以用全概率公式展开。接着依次计算属于每个类别的概率。
(下为贝叶斯公式:)
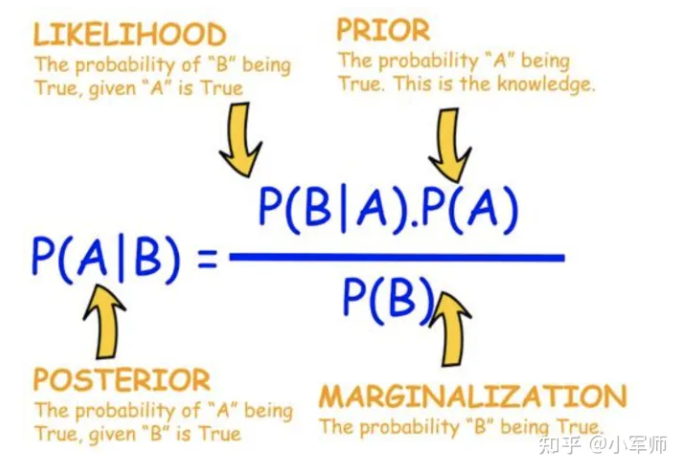
计算完后,取出类别概率最大的类别 c j c_j cj,则属于 c j c_j cj类。
x.3 使用朴素贝叶斯做分类
如果没理解的话,直接跳到x.6看例子。
补充一下全概率公式,已知 B 1 , . . . , B n B_1, ... , B_n B1,...,Bn是一个完备事件组且两两互斥:
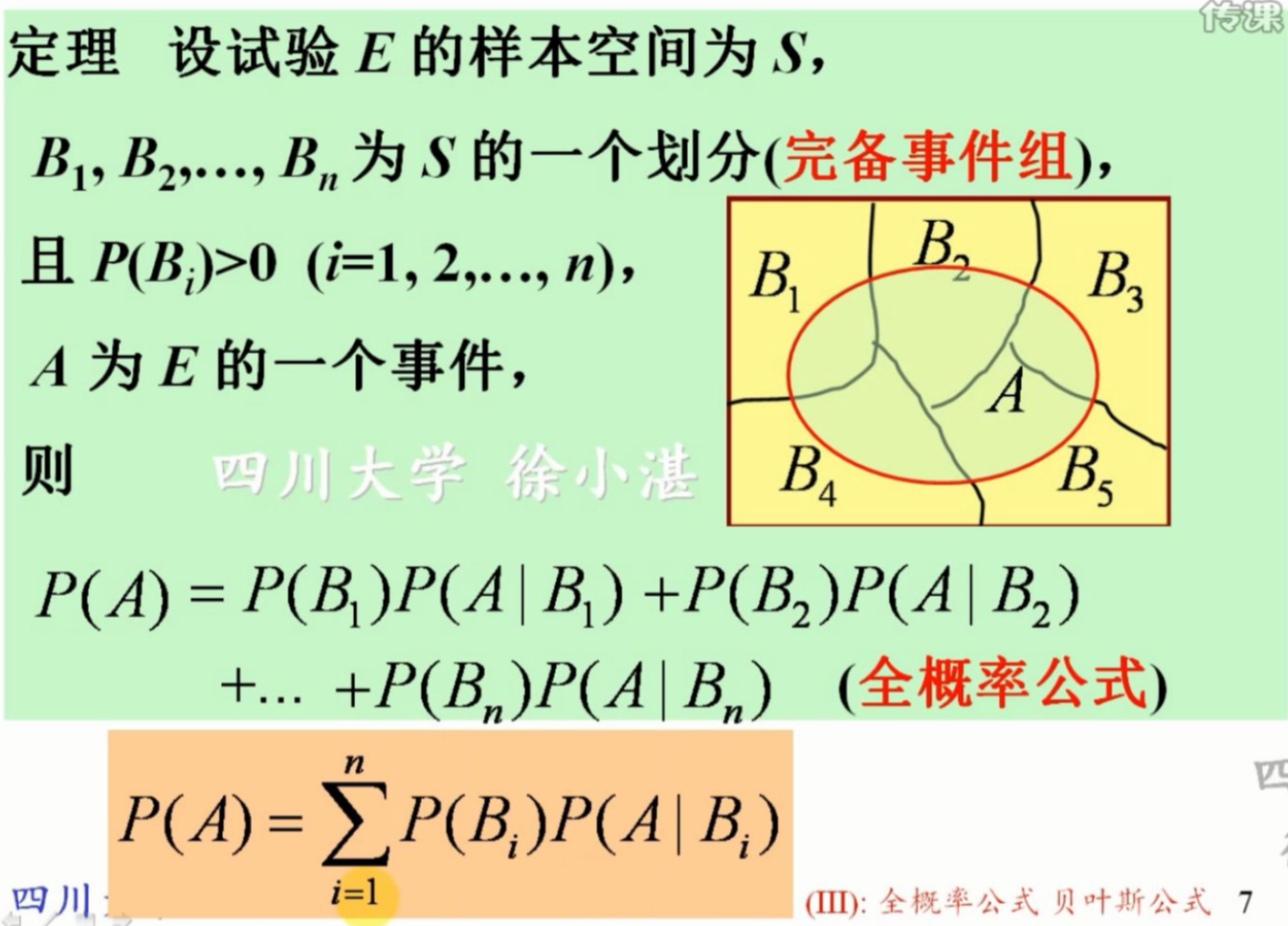
在求取后验概率时,使用贝叶斯定理做变换后,得到式子 P ( Y = c i ∣ X = x ) = P ( Y = c i ) P ( X = x ∣ Y = c i ) P ( X = x ) P(Y=c_i|X=x)=\frac {P(Y=c_i)P(X=x|Y=c_i)}{P(X=x)} P(Y=ci∣X=x)=P(X=x)P(Y=ci)P(X=x∣Y=ci),分母用全概率公式展开,得到下式:
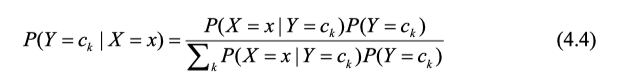
根据条件独立性假设推导条件概率展开式如下:
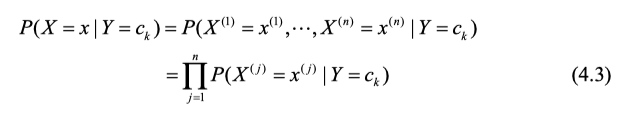
例如一个样本,它的特征取值是 x j ( 1 ) , . . . , x i ( n ) x_j^{(1)}, ... , x_i^{(n)} xj(1),...,xi(n)则你需要将这些值带入,就变成了上面第一行右边的式子,再根据独立性质展开即得(4.3)。
将(4.3)带入贝叶斯展开式(4.4),得到如下式子:
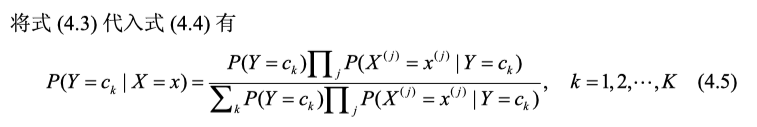
于是朴素贝叶斯分类器就变成了如下式:
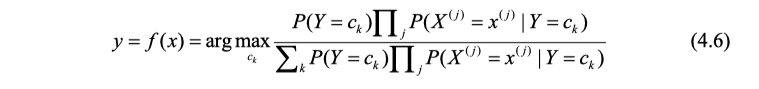
通过观察我们可以看到对于不同大类 c k c_k ck,分母都是相同的,只要考察分子便可,于是将(4.6)化简得到如下:
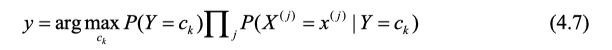
我们注意到最终的后验概率=先验概率*j个条件概率乘积。
x.4 后验概率最大化的含义
后验概率最大化的概率=期望风险最小化准则。这便是朴素贝叶斯采用的原理。详见统计学习分析4.1.2。
x.5 朴素贝叶斯法的参数估计
参数估计采用了Maximum Likelihood Estimation(MLE,极大似然估计)。极大似然估计即求让似然函数最大值的参数,在一堆样本中数数即等于极大似然估计法,为什么可以看下面的推导:

使用极大似然估计法求后验概率展开式分子中的先验概率和条件概率如下:
先验概率,直接数数便可得:
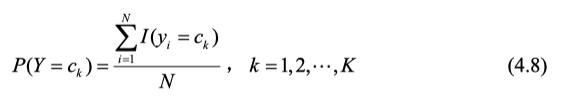
条件概率,使用条件概率展开式展开成乘积的格式,再数数可得:
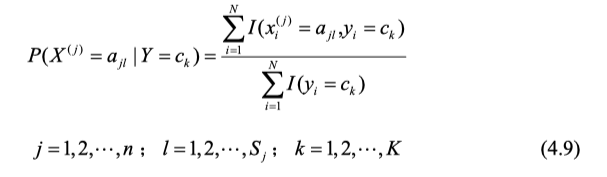
其中有j个特征,第j个特征有 S j S_j Sj个取值,y有k个大类。
x.6 朴素贝叶斯例子
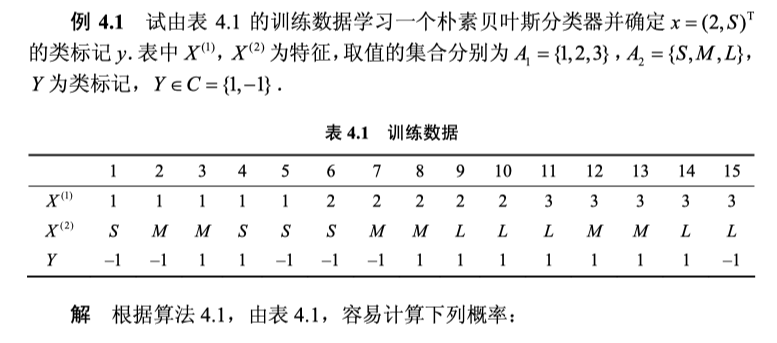
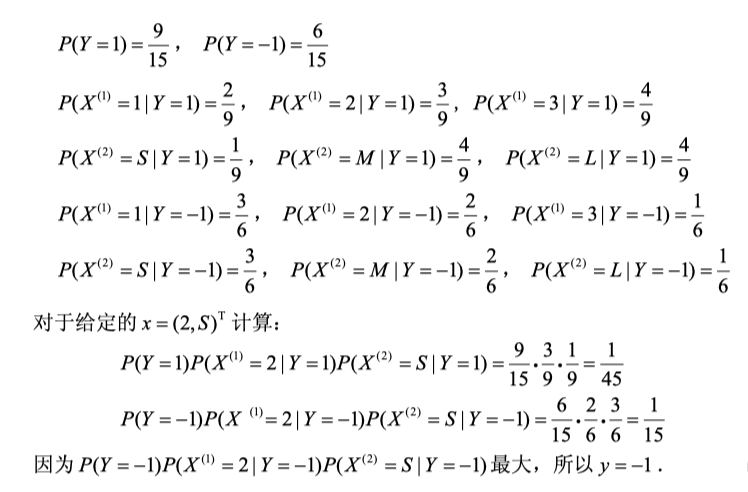
x.7 贝叶斯估计
即在参数估计时,用贝叶斯估计代替MLE。因为在例如用女儿国做样本,估计人群中男生比例时,往往会出现所要估计的概率值为0的情况,这时候会影响到后验概率的计算结果,使分类产生偏差,所以引入贝叶斯估计,如下:


如此便不会出现概率全0的情况。
相关文章:

统计学习方法第四章——朴素贝叶斯法
x.1 前言 朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。是通过给定training dataset学习联合概率分布的方法,是一种生成方法。 x.2 使用贝叶斯定理做分类 使用贝叶斯定理做分类,相比较于朴素贝叶斯即丢除特征条件独立假设这个条件。 …...
安装配置goaccess实现可视化并实时监控nginx的访问日志
一、业务需求 我们安装了nginx后,需要对nginx的访问情况进行监控(希望能够实时查看到访问nginx的情况),如下图所示: 二、goaccess的安装配置步骤 2.1、准备内容 需要先安装配置nginx或OpenResty - 安装 Linux环境对Nginx开源版源码下载、编译、安装、开机自启https://b…...
springboot第14集:MyBatis-CRUD讲解
注意点:增、删、改操作需要提交事务! 为了规范操作,在SQL的配置文件中,我们尽量将Parameter参数和resultType都写上! 编写Mapper接口类 import com.da.pojo.User; import java.util.List; public interface UserMapper…...

ES6新特性(1)
目录 一、字符串扩展 (1)字符串遍历器接口(for...of...) (2)模板字符串 二、字符串新增方法 (1)包含方法 (2)重复方法 (3)补全方…...
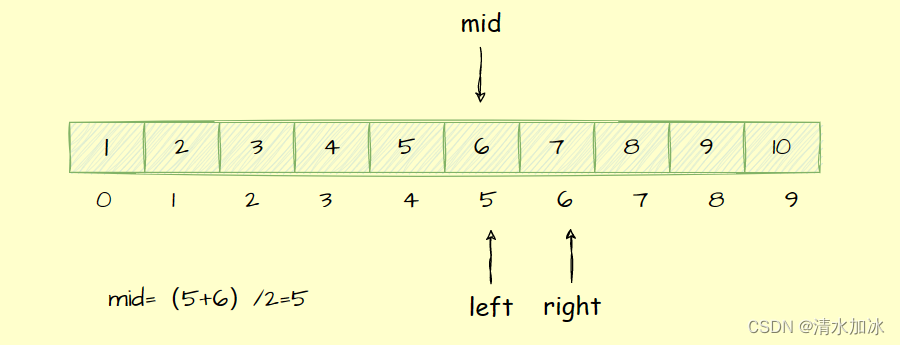
这就是二分查找?(C语言版)
大家好!我又来了,哈哈~今天我要和大家分享一种神奇的算法——二分查找!你可能会问,“二分查找有什么好玩的?”但在我看来它就像一场魔法表演,当你输入一个数,他会在一堆数中快速找到它的位置。找…...

操作系统之内存管理
连续分配 一、单一连续 直接为要运行的进程分配一个内存,只适合单任务,只能用于单对象、单任务,内存被分配为系统区和用户区,系统区在低地址,用户区是一个用户独享 二、等分分区 由于分配一个内存只能执行单任务&a…...
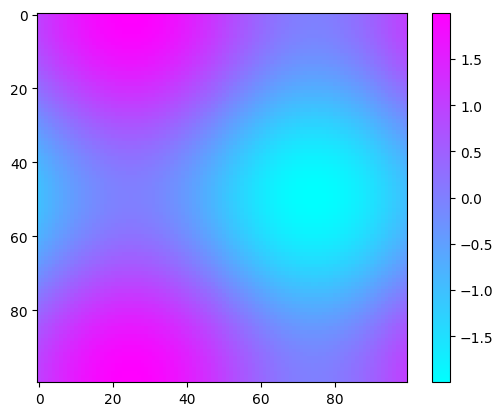
【Python | matplotlib】matplotlib.cm的理解以及举例说明
文章目录 一、模块介绍二、颜色举例 一、模块介绍 matplotlib.cm是Matplotlib中的一个模块,它提供了一组用于处理颜色映射(colormap)的函数和类。颜色映射是一种将数值映射到颜色的方法,常用于制作热力图、等值线图、散点图等。 …...
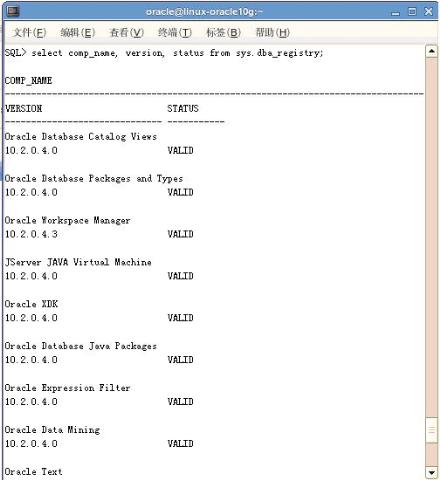
数据库单实例升级
一、单实例环境,全时长二个半钟多。详细图文说明到这下载 1、停止所有oracle相关进程。 Emctlstop dbconsole Isqlplusctl stop Lsnrctl stop sqlplus /nolog sql>conn /as sysdba Connectedtoanidleinstance. sql>shutdown 然后,冷备份下数据库cp…...

Photoshop如何使用选区之实例演示?
文章目录 0.引言1.利用快速选择工具抠图2.制作网店产品优惠券3.利用选区改变眼睛颜色4.抠取复杂的花束5.制作丁达尔光照效果6.利用选区调整图像局部颜色 0.引言 因科研等多场景需要进行绘图处理,笔者对PS进行了学习,本文通过《Photoshop2021入门教程》及…...

ThreadLocal的使用介绍和底层原理解析和开源框架的使用实例
文章目录 ThreadLocal的使用介绍和底层原理解析和开源框架的使用实例ThreadLocal简介ThreadLocal使用示例ThreadLocal原理解析Spring中ThreadLocal的应用小结ThreadLocal的使用步骤常见面试题案例解析(框架源码经典案例)案例实战 ThreadLocal的使用介绍和底层原理解析和开源框架…...

带你学c带你飞-P7取值范围
比特位 CPU能读懂的最小单元——比特位,bit,b 字节 内存机构的最小寻址单元——字节,Byte,B 1Byte8bit 进制 怎么算 注意:int默认是signed类型,signed类型第一位是符号位 符号位 存放signed类型的存…...

ramfs, rootfsinitramfs
什么是ramfs? ramfs是一个非常简单的文件系统,它将Linux的磁盘缓存机制(页面缓存和dentry缓存)导出为一个动态可调整大小的基于ram的文件系统。 Linux通常将所有文件缓存在内存中。从后备存储(通常是挂载文件系统的块设备)读取的数据页被保留下来,以防…...
)
十三届蓝桥杯研究生组国赛-最大公约数(线段树+二分)
十三届蓝桥杯研究生组国赛-最大公约数 1、问题描述2、解题思路2.1 解法一:暴力查询区间gcd(75%)2.2 解法二:线段树+二分法(AC)1、问题描述 问题描述 给定一个数组, 每次操作可以选择数组中任意两个相邻的元素 x , y x,y x,y...

数据结构——二叉树层序遍历
数据结构——二叉树层序遍历 107. 二叉树的层序遍历 II199. 二叉树的右视图思路: 637. 二叉树的层平均值 107. 二叉树的层序遍历 II 107. 二叉树的层序遍历 II 给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节…...
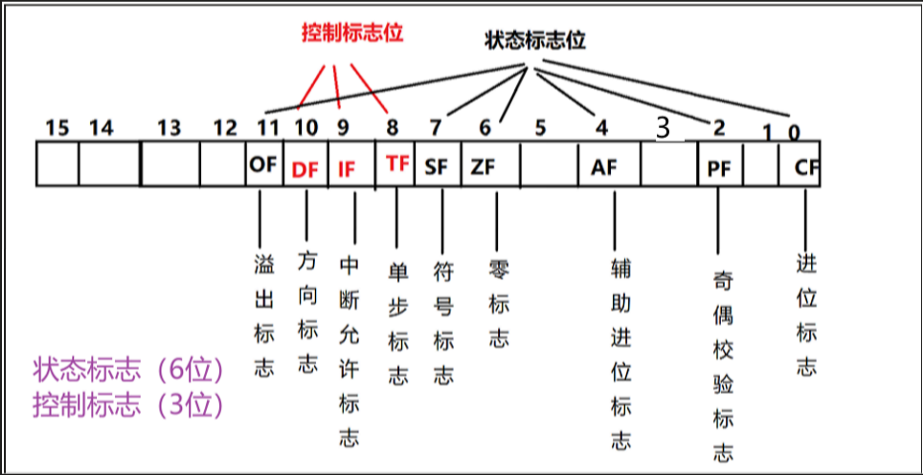
【微机原理】8088/8086微处理器
目录 一、8088/8086的功能结构 1.总线接口部件(BIU) 2.执行部件(EU) 二、8088/8086的寄存器结构(14个) 溢出标志的概念 溢出和进位的区别 8086CPU是Intel系列的16位微处理器,他有16根数据…...

springboot第12集:DAO功能代码
在Spring Boot中,DAO是数据访问对象的缩写,它是一种设计模式用于提供对数据库操作的抽象层。通过使用DAO模式,我们可以将数据操作与业务逻辑分离,并提供一个单独的接口来执行所有的数据库操作。 在Spring Boot中,通常使…...

基于KZG多项式承诺方案的RLN
1. 引言 RLN——Rate-Limiting Nullifier为PSE团队主导的项目,源自: Barry White Hat 2019年博客 Semaphore RLN, rate limiting nullifier for spam prevention in anonymous p2p setting RLN(Rate-Limiting Nullifier)是一种…...
《站在巨人的肩膀上学习Java》
Java从诞生距今已经有28年了,在这段时间里,随着Java版本的不断迭代,Java新特性的不断出现,使得Java被使用的越来越广泛。在工程界Java语言一直是大家最喜欢的语言之一,Java一直排行在编程语言热门程度的前3名。 可想而…...
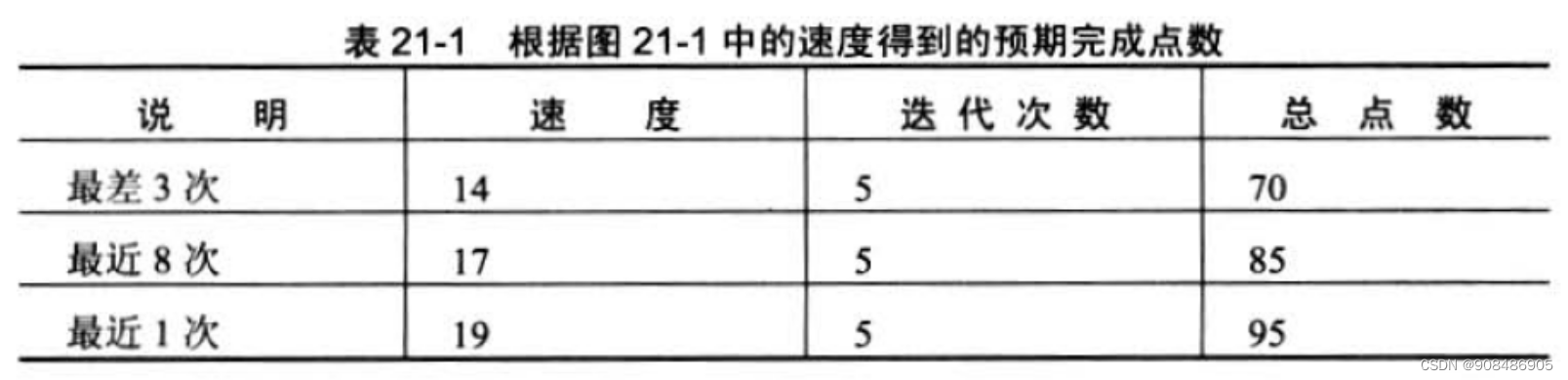
敏捷ACP.敏捷估计与规划.Mike Cohn.
第一部分 传统规划失败的原因 vs 敏捷规划有效的原因 传统的项目规划方式往往会让我们失望。要回答-一个 新产品的范围/进度/资源的组合问题,传统规划过程不一定会产生令人非常满意的答案和最终产品。以下- -些论据可以支持这个结论: ●大约2/3的项目会显著超…...
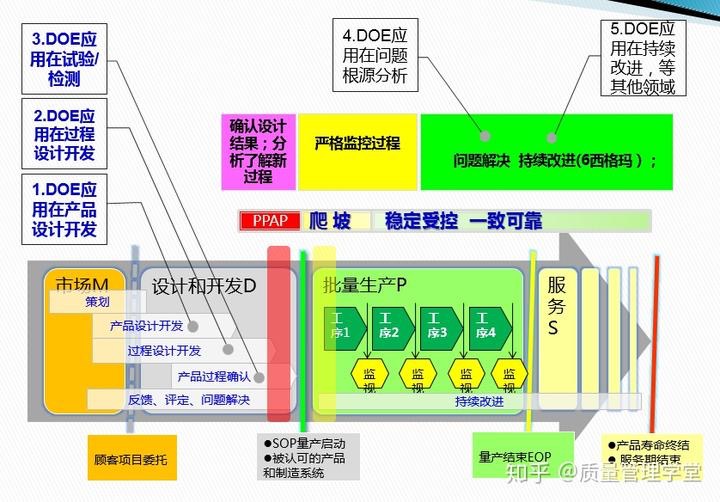
[创新工具和方法论]-01- DOE课程基础知识
文章目录 1.DOE实验设计的介绍1.1 什么是实验设计DOE?1.2 DOE的优势有哪些?1.3 如何开展DoE研究?步骤 2.DOE实验培训3.数据分析步骤4.实验的随机化5.偏差6.R方 相关系数假设检验 7.三因子二水平全因子设计 1.DOE实验设计的介绍 实验设计是一种安排实验和分析实验数…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
