基于KZG多项式承诺方案的RLN
1. 引言
RLN——Rate-Limiting Nullifier为PSE团队主导的项目,源自:
- Barry White Hat 2019年博客 Semaphore RLN, rate limiting nullifier for spam prevention in anonymous p2p setting
RLN(Rate-Limiting Nullifier)是一种zk小工具/协议,可为匿名环境启用垃圾邮件预防机制。旨在:
- 在每个epoch使用KZG多项式承诺
- 为每个message使用KZG opening
- 为单个message生成proof的时间应小于1ms,几乎改进约1000倍
- 使用RLN作为垃圾邮件保护层(spam protection layer),从而具有网络层面的隐私,可用于Tor网络和以太坊validator网路
从技术层面上来说,transmitter选中某多项式 f ( X ) f(X) f(X),其中 f ( 0 ) f(0) f(0)为其想要保护的私钥,当发送某message时,实际发送的是该多项式上的某个点。
若 f ( X ) f(X) f(X)为 n n n阶多相似,则所发送的message数量上限为 n n n,transmitter若发送多于 n n n个不同的message,则其私钥将会泄露。
实际使用zkSNARK来:
- 使用membership proof,来确保transmitter对某proof of stake进行了承诺
- 使用message proof,来证明其包含了多项式上的某个点。
当前的问题在于,为单个message来生成proof需约1s,在很多场景下并不实用——如Tor网路、Validator网络、手机环境等。需要利用KZG多项式承诺和KZG opening方案,将单个message证明时间由1s提高到1ms。
具体场景为:
- 某指定epoch e e e和message数量上限(message limit) n n n,用户创建某degree为 n n n的多项式,满足 f ( 0 ) f(0) f(0)为该用户的私钥 p k pk pk。
- 可信设置(trusted setup):
- 对于message数量上限为 n n n的场景,需要shared common reference: g , g α , g α 2 , ⋯ , g α n g,g^{\alpha}, g^{\alpha^2},\cdots,g^{\alpha^n} g,gα,gα2,⋯,gαn
- 对于非匿名版本:需为每个message limit执行可信设置。
- 对于匿名版本:可使用现有的reference。
- 对于message数量上限为 n n n的场景,需要shared common reference: g , g α , g α 2 , ⋯ , g α n g,g^{\alpha}, g^{\alpha^2},\cdots,g^{\alpha^n} g,gα,gα2,⋯,gαn
承诺是指:
- 用户为某epoch选中某 n n n-degree多项式,最多可发送 n n n个message,其中 f ( 0 ) f(0) f(0)为用户私钥 p k pk pk。
- 使用reference string用户计算KZG多项式承诺 C = g f ( α ) C=g^{f(\alpha)} C=gf(α)。
- 在特定epcoh,用户分享该多项式承诺 C C C。
- 为发送某message,用户分享 ( f ( m ) , g ψ m ( α ) ) (f(m), g^{\psi_m(\alpha)}) (f(m),gψm(α)),其中 m m m为message的哈希值, g ψ m ( α ) g^{\psi_m(\alpha)} gψm(α)为相应的opening proof,其中 ψ m ( x ) = f ( x ) − f ( m ) x − m \psi_m(x)=\frac{f(x)-f(m)}{x-m} ψm(x)=x−mf(x)−f(m)。
对某message的evaluation为:
- 计算message的哈希值: m m m
- RLN message为: m , f ( m ) , g ψ m ( α ) m,f(m),g^{\psi_m(\alpha)} m,f(m),gψm(α)
- Verifier具有该epoch的多项式承诺值 g f ( α ) g^{f(\alpha)} gf(α)
- Verifier对message进行evaluate:
e ( g f ( α ) , g ) = ? e ( g ψ m ( α ) , g α ⋅ g − m ) ⋅ e ( g , g ) f ( m ) e(g^{f(\alpha)},g)\overset{\text{?}}{=}e(g^{\psi_m(\alpha)},g^{\alpha}\cdot g^{-m})\cdot e(g,g)^{f(m)} e(gf(α),g)=?e(gψm(α),gα⋅g−m)⋅e(g,g)f(m)
为此,设计了3个版本:
- Version A:具体的原型设计见:
https://github.com/Rate-Limiting-Nullifier/kzg-rln/blob/main/versionA/src/main.rs(Rust) - Version B
- Version C
这3个版本的性能对比为:【可在epoch之初缓存 e ( g f ( α ) , g ) e(g^{f(\alpha)},g) e(gf(α),g)以供之后的message verification过程中使用,因此,每个message verification仅需2次pairing运算。】

2. Version A:非匿名的最简单方案
关键点为:
- 用户的公钥为: g f ( 0 ) g^{f(0)} gf(0)
- 用户提供多项式承诺值、用户公钥以及opening proof: g f ( α ) , g ψ 0 ( α ) , g f ( 0 ) g^{f(\alpha)},g^{\psi_0(\alpha)},g^{f(0)} gf(α),gψ0(α),gf(0)
- Verifier:通过验证KZG commitment的opening,检查用户公钥 g f ( 0 ) g^{f(0)} gf(0)在所承诺的多项式上。
e ( g ψ 0 ( α ) , g α ) ⋅ e ( g , g f ( 0 ) ) = ? e ( g , g f ( α ) ) e(g^{\psi_0(\alpha)},g^{\alpha})\cdot e(g,g^{f(0)})\overset{\text{?}}{=}e(g,g^{f(\alpha)}) e(gψ0(α),gα)⋅e(g,gf(0))=?e(g,gf(α))
3. Version B:借助ZKP实现的匿名方案
ZKP针对的场景为:
- public信息有: g f ( α ) , n g^{f(\alpha)},n gf(α),n
- private信息有: f ( x ) , p k f(x),pk f(x),pk
- 约束有:
- f ( 0 ) = p k f(0)=pk f(0)=pk
- membership proof of g f ( 0 ) g^{f(0)} gf(0)
- f ( x ) = ∑ i = 0 k c i x i f(x)=\sum_{i=0}^{k}c_ix^i f(x)=∑i=0kcixi,当 i > n i>n i>n时有 c i = 0 c_i=0 ci=0
用户提供proof π \pi π和多项式承诺值 g f ( α ) g^{f(\alpha)} gf(α)。
Verifier检查proof:
verify ( π , g f ( α ) , root , n ) → t r u e \text{verify}(\pi, g^{f(\alpha)},\text{root},n)\to true verify(π,gf(α),root,n)→true
4. Version C:为多个epoch承诺 使用multiple多项式承诺 的匿名方案
multiple多项式承诺方案为:
- 用户为 m m m个epoch创建 m m m个degree为 n n n的多项式,然后对这些多项式同时承诺。
- 对于某epoch,对应的 n n n-degree多项式为 f e ( x ) f_e(x) fe(x),将其表示为 f e ( x ) = ∑ i = 0 n c i ( e ) ⋅ x i f_e(x)=\sum_{i=0}^{n}c_i(e)\cdot x^i fe(x)=∑i=0nci(e)⋅xi,从而有:
f 1 ( x ) = c 0 ( 1 ) + c 1 ( 1 ) x + c 2 ( 1 ) x 2 + ⋯ + c n ( 1 ) x n f_1(x)=c_0(1)+c_1(1)x+c_2(1)x^2+\cdots+c_n(1)x^n f1(x)=c0(1)+c1(1)x+c2(1)x2+⋯+cn(1)xn
f 2 ( x ) = c 0 ( 2 ) + c 1 ( 2 ) x + c 2 ( 2 ) x 2 + ⋯ + c n ( 2 ) x n f_2(x)=c_0(2)+c_1(2)x+c_2(2)x^2+\cdots+c_n(2)x^n f2(x)=c0(2)+c1(2)x+c2(2)x2+⋯+cn(2)xn
f 3 ( x ) = c 0 ( 3 ) + c 1 ( 3 ) x + c 2 ( 3 ) x 2 + ⋯ + c n ( 3 ) x n f_3(x)=c_0(3)+c_1(3)x+c_2(3)x^2+\cdots+c_n(3)x^n f3(x)=c0(3)+c1(3)x+c2(3)x2+⋯+cn(3)xn
⋮ \vdots ⋮
f m ( x ) = c 0 ( m ) + c 1 ( m ) x + c 2 ( m ) x 2 + ⋯ + c n ( m ) x n f_m(x)=c_0(m)+c_1(m)x+c_2(m)x^2+\cdots+c_n(m)x^n fm(x)=c0(m)+c1(m)x+c2(m)x2+⋯+cn(m)xn - 用户为每个 c i ( e ) c_i(e) ci(e)创建多项式承诺
对应ZKP针对的场景为:
- public信息有: g c i ( α ) , n , m g^{c_i(\alpha)},n,m gci(α),n,m
- private信息有: c i ( e ) , p k c_i(e),pk ci(e),pk
- 约束有:
- 对于每个 e ≤ m e\leq m e≤m,有 c 0 ( e ) = p k c_0(e)=pk c0(e)=pk
- f e ( x ) = ∑ i = 0 k c i ( e ) x i f_e(x)=\sum_{i=0}^{k}c_i(e)x^i fe(x)=∑i=0kci(e)xi,当 i > n i>n i>n,有 c i ( e ) = 0 c_i(e)=0 ci(e)=0
- membership proof of g f e ( 0 ) g^{f_e(0)} gfe(0)
- 多项式承诺值 g c i ( α ) g^{c_i(\alpha)} gci(α)是正确的
验证过程为:
- 对于注册阶段:
- Verifier检查proot:
verify ( π , g c 0 ( α ) , ⋯ , g c n ( α ) , root , n , m ) → t r u e \text{verify}(\pi, g^{c_0(\alpha)},\cdots,g^{c_n(\alpha)},\text{root},n,m)\to true verify(π,gc0(α),⋯,gcn(α),root,n,m)→true
- Verifier检查proot:
- 对于每个epoch e e e:
- 用户提交:
-
{ ( g c 0 ( e ) , g ϕ 0 , e ( α ) ) , ( g c 1 ( e ) , g ϕ 1 , e ( α ) ) , ⋯ , ( g c n ( e ) , g ϕ n , e ( α ) ) } \{(g^{c_0(e)},g^{\phi_{0,e}(\alpha)}),(g^{c_1(e)},g^{\phi_{1,e}(\alpha)}),\cdots,(g^{c_n(e)},g^{\phi_{n,e}(\alpha)})\} {(gc0(e),gϕ0,e(α)),(gc1(e),gϕ1,e(α)),⋯,(gcn(e),gϕn,e(α))},其中 ϕ ( i , e ) ( x ) = c i ( x ) − c i ( e ) x − e \phi_{(i,e)}(x)=\frac{c_i(x)-c_i(e)}{x-e} ϕ(i,e)(x)=x−eci(x)−ci(e)
-
为检查 g f e ( α ) = ∏ i = 0 n g c i ( e ) α i g^{f_e(\alpha)}=\prod_{i=0}^{n}g^{c_i(e)\alpha^i} gfe(α)=∏i=0ngci(e)αi,Verifier检查:
e ( g , g f e ( α ) ) = e ( g , ∏ i = 0 n g c i ( e ) α i ) = ? ∏ i = 0 n e ( g c i ( e ) , g α i ) e(g,g^{f_e(\alpha)})=e(g,\prod_{i=0}^{n}g^{c_i(e)\alpha^i})\overset{\text{?}}{=}\prod_{i=0}^{n}e(g^{c_i(e)},g^{\alpha^i}) e(g,gfe(α))=e(g,∏i=0ngci(e)αi)=?∏i=0ne(gci(e),gαi)- 对于 i = 0 , ⋯ , n i=0,\cdots,n i=0,⋯,n,借助同态属性,Verifier检查用户在多项式承诺值中隐藏的系数:
e ( g c i ( α ) , g ) = ? e ( g ϕ i , e ( α ) , g α ⋅ g − e ) ⋅ e ( g , g c i ( e ) ) e(g^{c_i(\alpha)},g)\overset{\text{?}}{=}e(g^{\phi_{i,e}(\alpha)},g^{\alpha}\cdot g^{-e})\cdot e(g,g^{c_i(e)}) e(gci(α),g)=?e(gϕi,e(α),gα⋅g−e)⋅e(g,gci(e))
其中 ϕ i , e ( x ) = c i ( x ) − c i ( e ) x − e \phi_{i,e}(x)=\frac{c_i(x)-c_i(e)}{x-e} ϕi,e(x)=x−eci(x)−ci(e)
- 对于 i = 0 , ⋯ , n i=0,\cdots,n i=0,⋯,n,借助同态属性,Verifier检查用户在多项式承诺值中隐藏的系数:
-
然后:
- 计算message的哈希值: m m m
- RLN message有: m , f ( m ) , g ψ m ( α ) m,f(m),g^{\psi_m(\alpha)} m,f(m),gψm(α)
- Verifier evaluate the message:
e ( g f ( α ) , g ) = ? e ( g ψ m ( α ) , g α ⋅ g − m ) ⋅ e ( g , g ) f ( m ) e(g^{f(\alpha)},g)\overset{\text{?}}{=}e(g^{\psi_m(\alpha)},g^{\alpha}\cdot g^{-m})\cdot e(g,g)^{f(m)} e(gf(α),g)=?e(gψm(α),gα⋅g−m)⋅e(g,g)f(m)
-
- 用户提交:
参考资料
[1] 2023年4月 ethresearch和zkresearch联合发布 RLN on KZG polynomial commitment scheme [cross-posted]
相关文章:

基于KZG多项式承诺方案的RLN
1. 引言 RLN——Rate-Limiting Nullifier为PSE团队主导的项目,源自: Barry White Hat 2019年博客 Semaphore RLN, rate limiting nullifier for spam prevention in anonymous p2p setting RLN(Rate-Limiting Nullifier)是一种…...
《站在巨人的肩膀上学习Java》
Java从诞生距今已经有28年了,在这段时间里,随着Java版本的不断迭代,Java新特性的不断出现,使得Java被使用的越来越广泛。在工程界Java语言一直是大家最喜欢的语言之一,Java一直排行在编程语言热门程度的前3名。 可想而…...
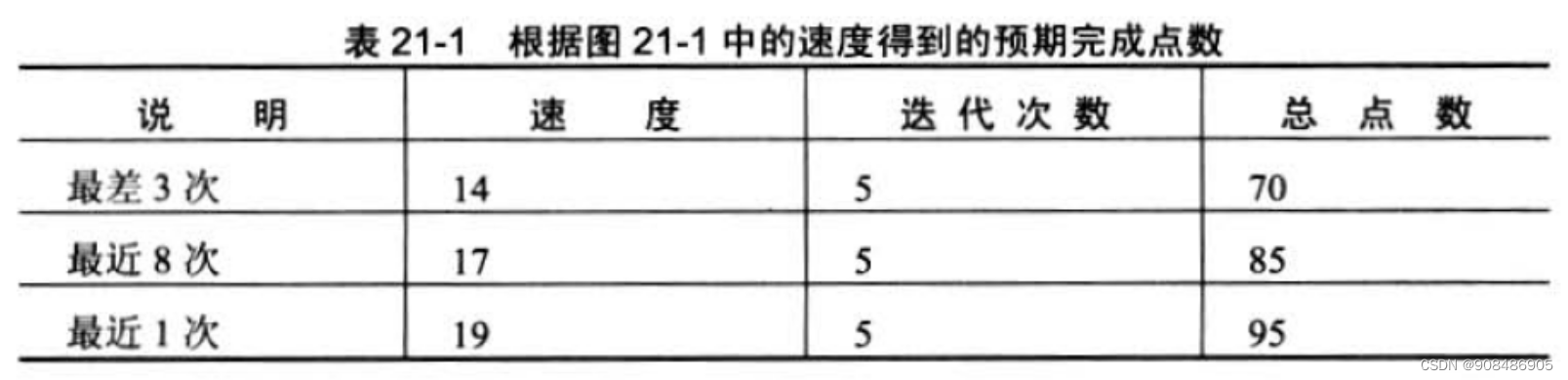
敏捷ACP.敏捷估计与规划.Mike Cohn.
第一部分 传统规划失败的原因 vs 敏捷规划有效的原因 传统的项目规划方式往往会让我们失望。要回答-一个 新产品的范围/进度/资源的组合问题,传统规划过程不一定会产生令人非常满意的答案和最终产品。以下- -些论据可以支持这个结论: ●大约2/3的项目会显著超…...
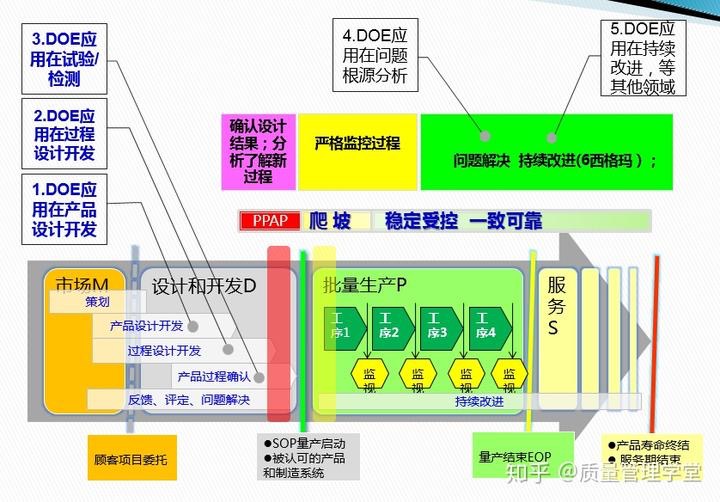
[创新工具和方法论]-01- DOE课程基础知识
文章目录 1.DOE实验设计的介绍1.1 什么是实验设计DOE?1.2 DOE的优势有哪些?1.3 如何开展DoE研究?步骤 2.DOE实验培训3.数据分析步骤4.实验的随机化5.偏差6.R方 相关系数假设检验 7.三因子二水平全因子设计 1.DOE实验设计的介绍 实验设计是一种安排实验和分析实验数…...
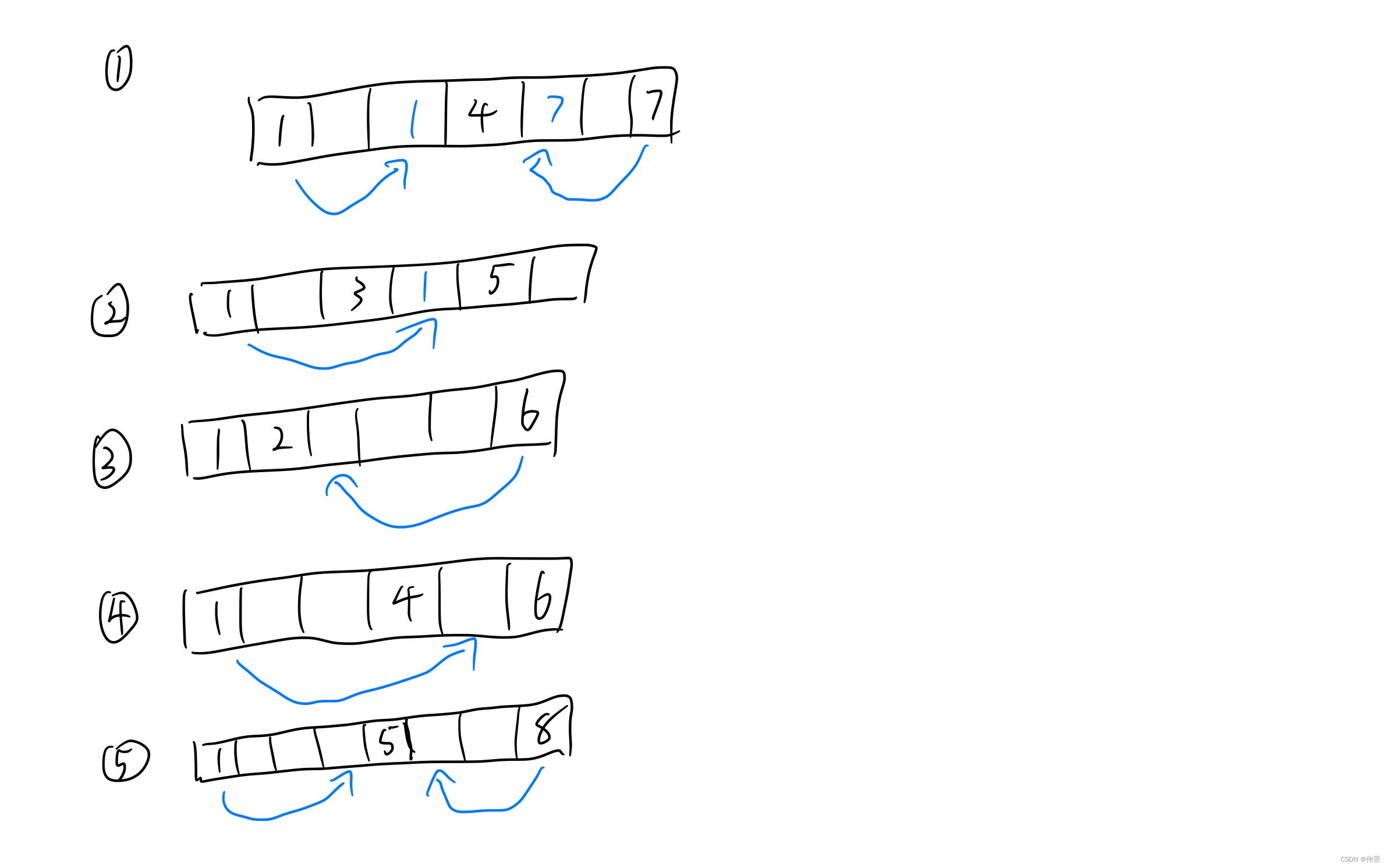
LeetCode-1033. 移动石子直到连续
题目链接 LeetCode-1033. 移动石子直到连续 题目描述 题解 题解一(Java) 作者:仲景 这题目挺难懂的,得画画图才能更好的理解 这也是LeetCode的尿性,习惯了,非得整这种别人看不懂的鸟语 你可以这样理解&a…...

JVM调优入门指南:掌握步骤、参数和场景
前言 作为Java开发者,我们经常需要优化应用的性能,其中JVM调优是非常重要的一部分。在本文中,我们将介绍JVM调优的一般步骤和方法,了解JVM调优参数,如堆大小、新生代比例、GC算法等参数的作用和配置方式,并…...

基于JSP+MySQL的跳蚤市场网站设计与开发
摘 要 在当今社会,网络信息已经不是什么很陌生的词汇,每天都在这个信息时代里生活着并且享受着它带来的与众不同。网络购物可以说是飞速发展的,这种购物方式逐渐的影响着人们的衣食住行。所以利用计算机实现 跳蚤市场网站设计与开发势在必行。本网站是一个校园的跳蚤市场网…...
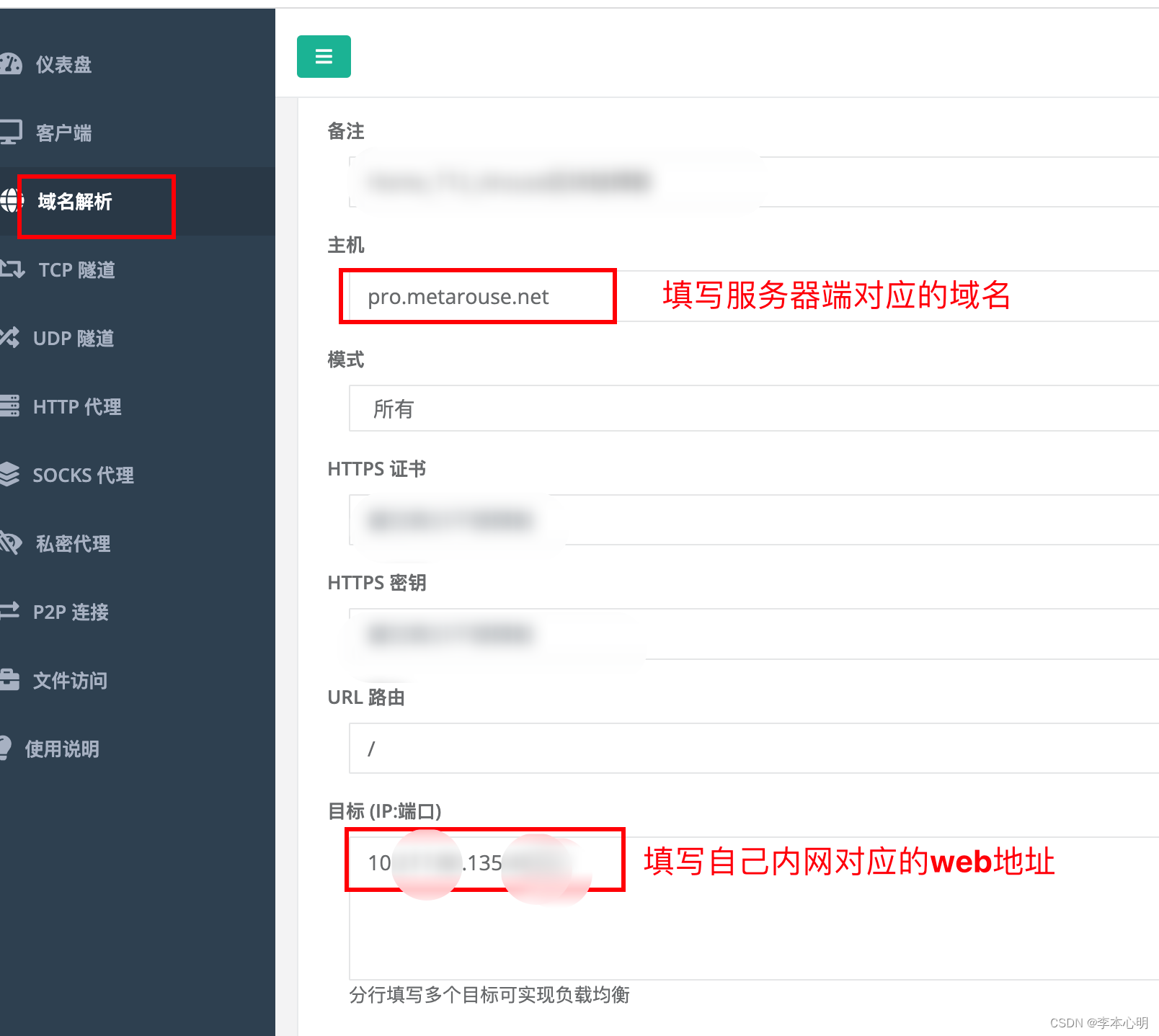
内网穿透NPS和宝塔Nginx配合使用,开启SSL访问本地局域网网络
并非为了教学,仅供自己记录,方便下次用。所以内容不会刻意花时间写的很细节详细。 1. 服务器NPS配置 NPS install安装后,配置文件会在其他位置,通过是 /etc/nps/nps.conf目录。 找到进行修改,主要修改的是http_proxy_p…...

ToLua框架
ToLua 是一个用于在 Unity 中为 Lua 提供 C# 语言绑定的框架。通过 ToLua,你可以方便地将 C# 代码暴露给 Lua 脚本,并在 Lua 脚本中调用 C# 类、方法和属性。 更新流程 原理:使用AssetBundle进行资源的更新,而由于lua运行时才编…...
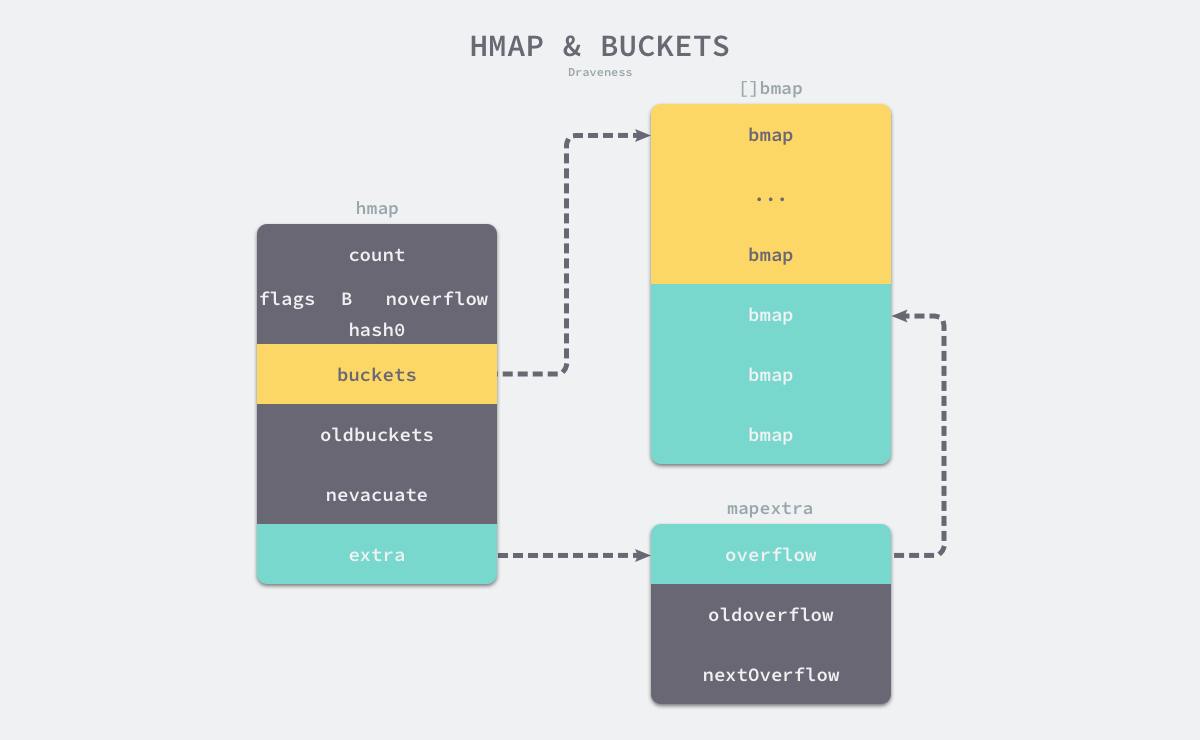
Golang-常见数据结构Map
Map map 是一种特殊的数据结构:一种元素对(pair)的无序集合,pair 的一个元素是 key,对应的另一个元素是 value,所以这个结构也称为关联数组或字典。这是一种快速寻找值的理想结构:给定 key&…...
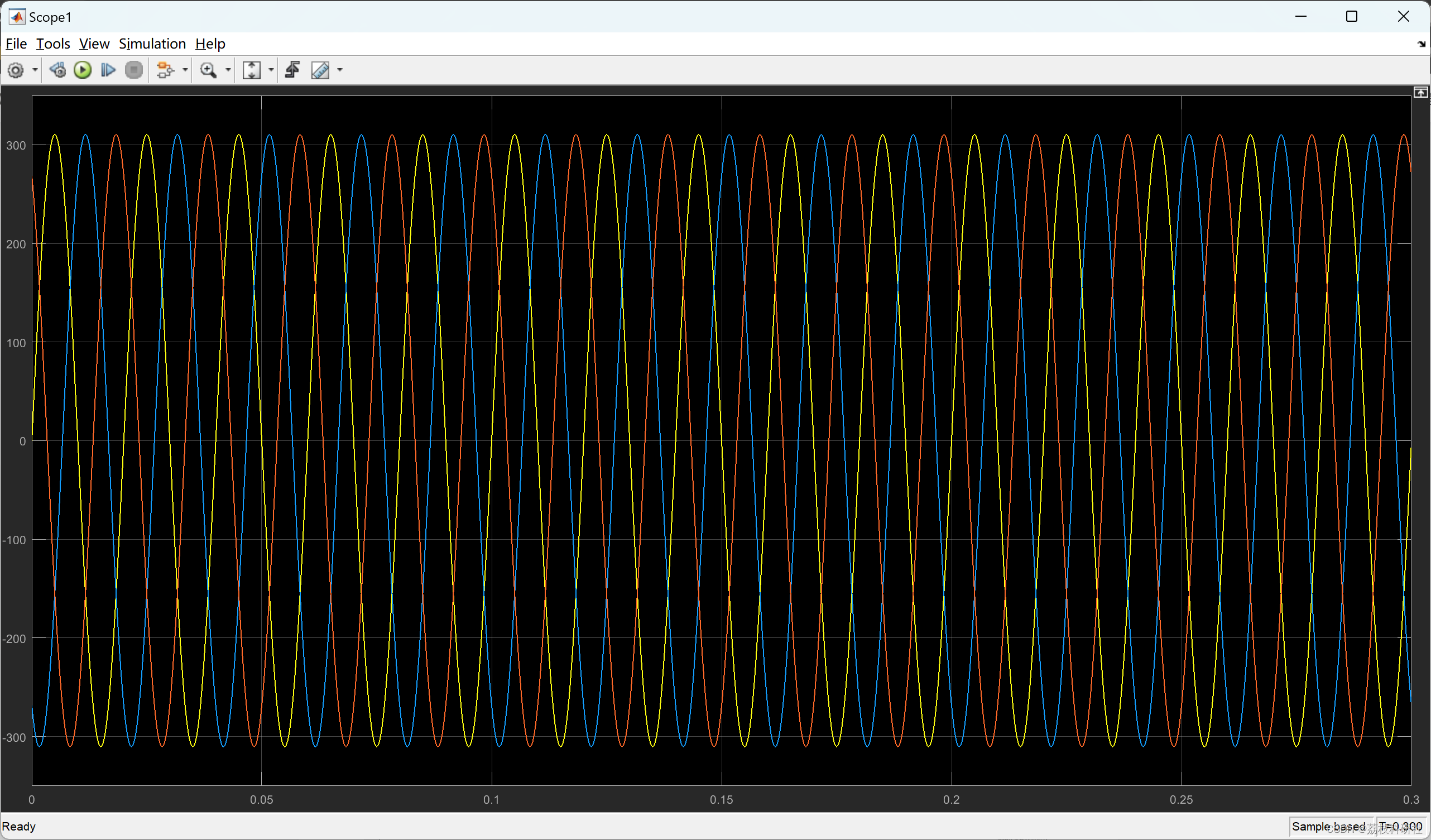
基于空间矢量脉宽调制(SVPWM)的并网逆变器研究(Simulink)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

介绍tcpdump在centos中的使用方法
tcpdump是一款强大的命令行数据包分析器,支持多种过滤和抓包参数。下面将介绍tcpdump的常用抓包参数。当需要监控CentOS系统的网络流量或者进行网络故障排查时,可以使用tcpdump来捕获数据包并进行分析。 下面介绍在CentOS中使用tcpdump的方法࿱…...
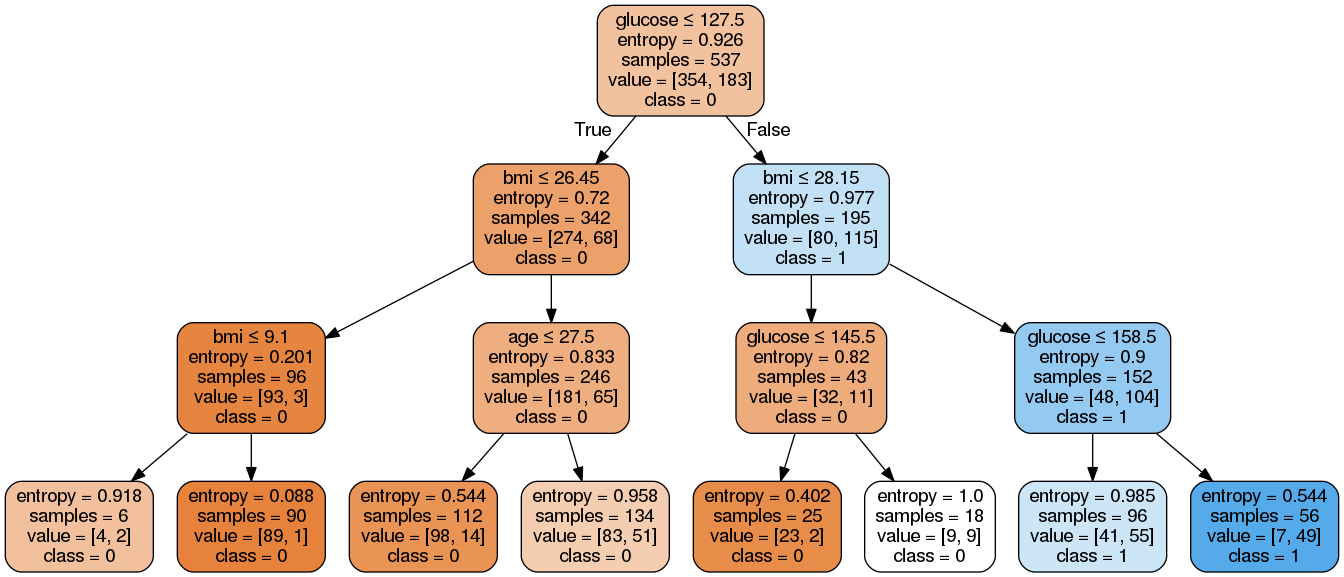
机器学习实战:Python基于DT决策树模型进行分类预测(六)
文章目录 1 前言1.1 决策树的介绍1.2 决策树的应用 2 Scikit-learn数据集演示2.1 导入函数2.2 导入数据2.3 建模2.4 评估模型2.5 可视化决策树2.6 优化模型2.7 可视化优化模型 3 讨论 1 前言 1.1 决策树的介绍 决策树(Decision Tree,DT)是一…...
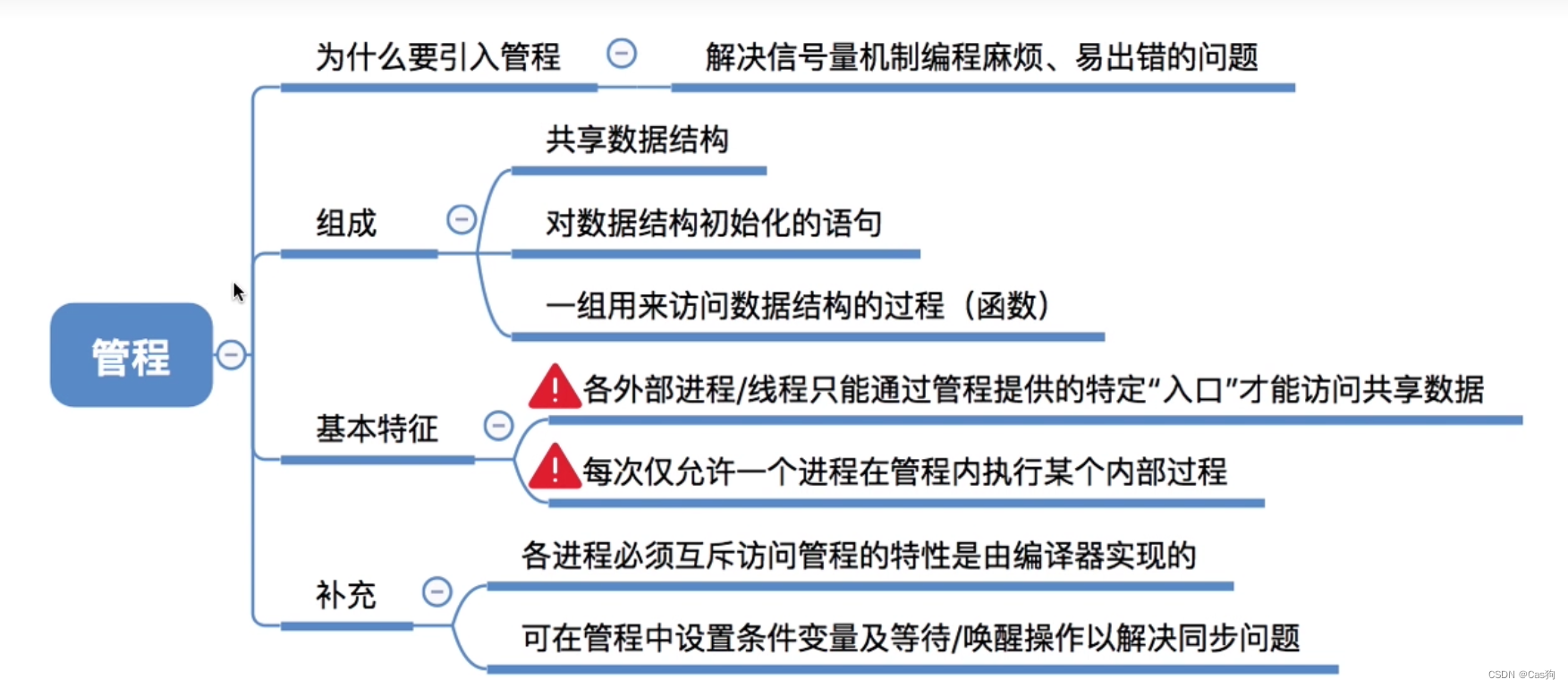
操作系统之进程同异步、互斥
引入 异步性是指,各并发执行的进程以各自独立的、不可预知的速度向前推进。 但是在一定的条件之下,需要进程按照一定的顺序去执行相关进程: 举例说明1: 举例说明2: 读进程和写进程并发地运行,由于并发必然导致异步性…...

你了解这2类神经性皮炎吗?常常预示着这5类疾病!
神经性皮炎属于慢性皮肤病,患者皮肤可出现局限性苔藓样变,同时伴有阵发性瘙痒。神经性皮炎易发生在颈部两侧和四肢伸侧,中年人是高发人群。到目前为止神经性皮炎病因还并不是很明确,不过一部分病人发病前常常出现精神神经方面异常…...
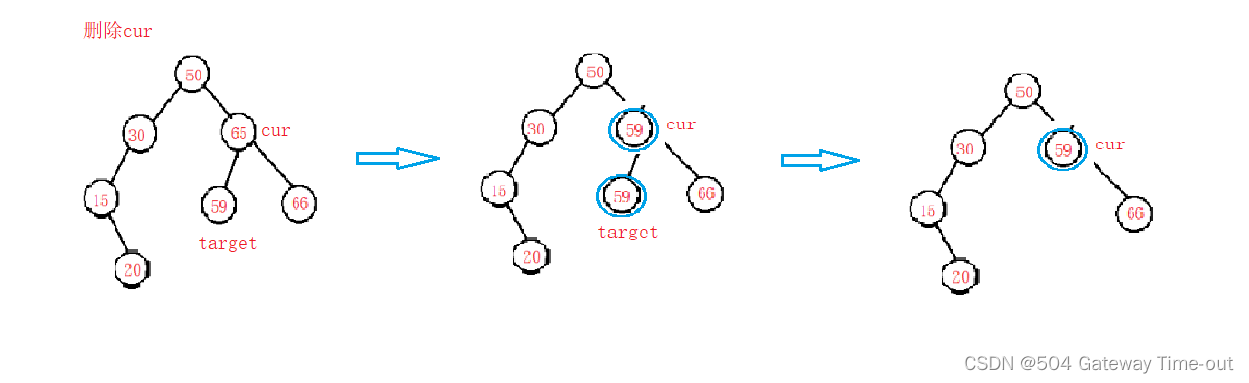
二叉搜索树【Java】
文章目录 二叉搜索树的性质二叉搜索树的操作遍历查找插入删除 二叉搜索树又称为二叉排序树,是一种具有一定性质的特殊的二叉树; 二叉搜索树的性质 若它的左子树不为空,则左子树上结点的值均小于根节点的值; 若它的右子树不为空&a…...

二叉树的遍历方式
文章目录 层序遍历——队列实现分析Java完整代码 先序遍历——中左右分析递归实现非递归实现——栈实现 中序遍历——左中右递归实现非递归实现——栈实现 后续遍历——左右中递归实现非递归实现——栈加标志指针实现 总结 层序遍历——队列实现 给你二叉树的根节点 root &…...
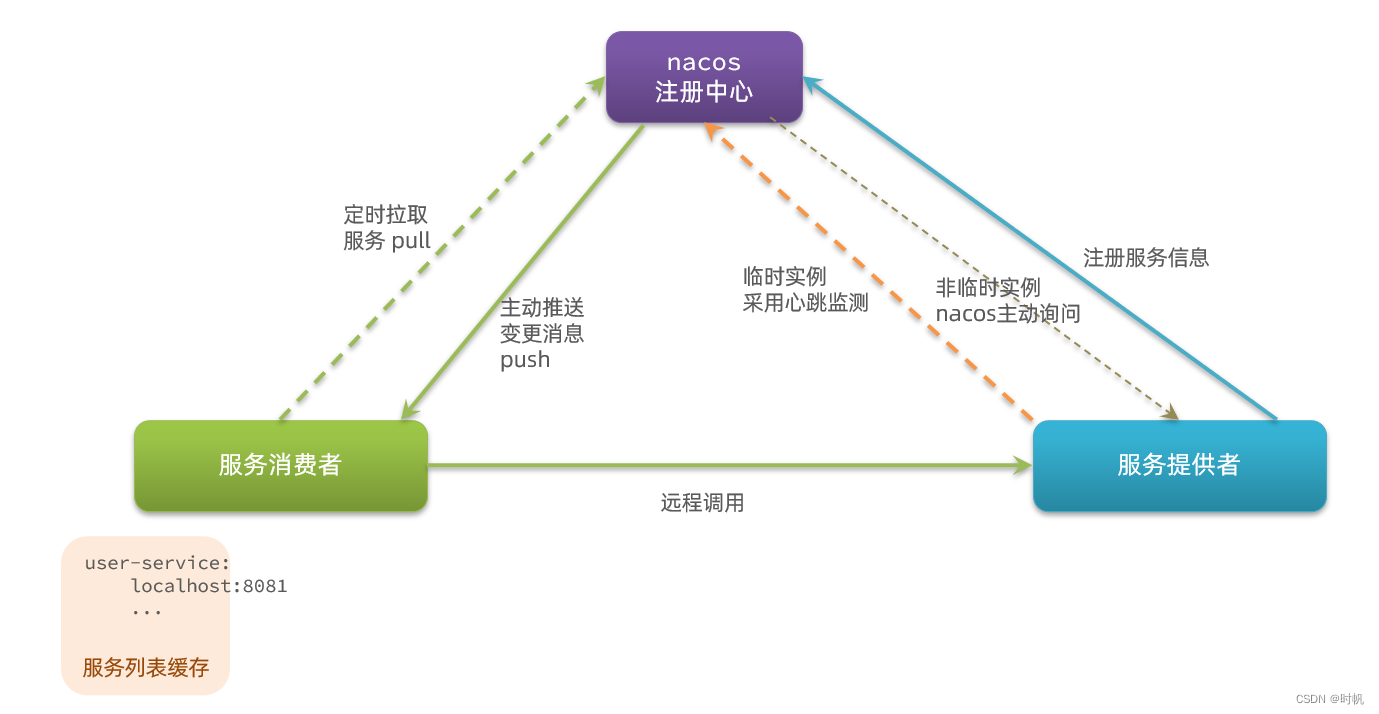
SpringCloud01
SpringCloud01 微服务入门案例 实现步骤 导入数据 实现远程调用 MapperScan("cn.itcast.order.mapper") SpringBootApplication public class OrderApplication {public static void main(String[] args) {SpringApplication.run(OrderApplication.class, args);}…...

SpringBoot整合Redis实现点赞、收藏功能
前言 点赞、收藏功能作为常见的社交功能,是众多Web应用中必不可少的功能之一。而redis作为一个基于内存的高性能key-value存储数据库,可以用来实现这些功能。 本文将介绍如何使用spring boot整合redis实现点赞、收藏功能,并提供前后端页面的…...

【Java入门合集】第一章Java概述
【Java入门合集】第一章Java概述 博主:命运之光 专栏:JAVA入门 学习目标 1.理解JVM、JRE、JDK的概念; 2.掌握Java开发环境的搭建,环境变量的配置; 3.掌握Java程序的编写、编译和运行; 4.学会编写第一个Java程序&#x…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
