[创新工具和方法论]-01- DOE课程基础知识
文章目录
- 1.DOE实验设计的介绍
- 1.1 什么是实验设计DOE?
- 1.2 DOE的优势有哪些?
- 1.3 如何开展DoE研究?
- 步骤
- 2.DOE实验培训
- 3.数据分析步骤
- 4.实验的随机化
- 5.偏差
- 6.R方 相关系数
- 假设检验
- 7.三因子二水平全因子设计
1.DOE实验设计的介绍
实验设计是一种安排实验和分析实验数据的数理统计方法。实验设计(DOE)是开发实验策略的工具,该策略可以使用最少的资源来最大程度地提高学习效果。DOE被广泛应用于许多领域,并在所有自然科学和社会科学中得到广泛应用。
1.1 什么是实验设计DOE?
实验设计(DoE)是一种优化反应和工艺的统计方法,允许不同因素同时发生变化,以便筛选出反应空间的较佳值。
在化学开发领域,由于实验设计(DoE)能使用少量实验评估大量反应参数,其已然成为一种加快反应优化的标准方法。 过去数年间,DoE一直被用于实施研发和制造领域的“质量源于设计”(QbD)。 在制药行业的QbD中,了解产品和工艺对确保产品生产质量至关重要。
1.2 DOE的优势有哪些?
由于DoE研究通常无需多次重复实验,因此DoE具有以下优势:
1).在更短的时间内更好地了解工艺
2).缩短制造领域的开发周期
1.3 如何开展DoE研究?
步骤
- 陈述实际的问题和实验的目的;
- 因果链分析,提取重要的因子;
- 选择Y的响应变量
- 陈述因子和水平
- 选择DOE实验设计
- 实施实验以及收集数据
- 分析实验结果
- 结论和计划
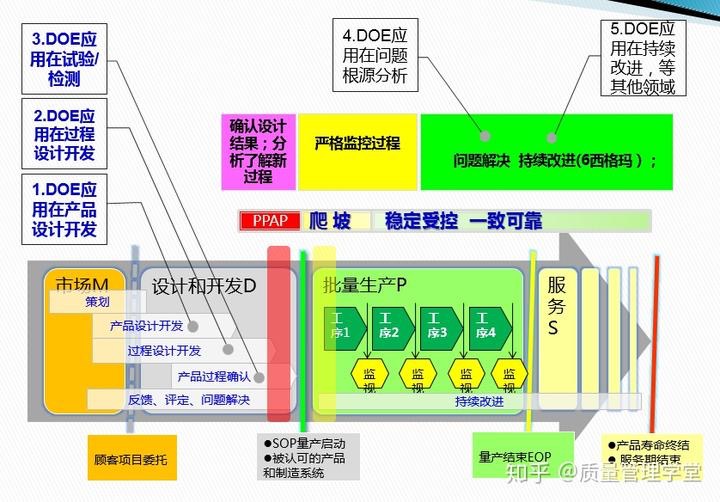
2.DOE实验培训
- 单因子实验法
- 正交实验:
- 判段x对于y的影响最大的
- 包括可控和不可控的x
- 明确关键性的工程和噪声变量
- 明确过程中需要仔细控制的变量
- 实验设计:
- x1的主效应: 高水平下y的均值- 低水平下y的均值
- 交互效应: 一个变量x1会影响x2对因变量的贡献度;也就是在x1在高水平和低水平不同的状态下,x2对y的贡献度不同.也叫协同效应.
3.数据分析步骤
- 实验数据检查
- 模型步骤拟合
- 提出非显著项
- 模型重新拟合
- 模型诊断
- 解释模型/验证
4.实验的随机化
- 重新排列顺序,消除或减小不可控因子的影响;
- 尽量减少本次实验不受前一次实验影响或者不影响下一次实验,保证实验的对立性;
- 实验次数大于系数个数25%至少 ,4个系数 拟合实验至少5次
- 验证实验25%-50%,4个系数 拟合实验至少2次
5.偏差
- 正态分布
- 随机性
- 均匀性
- 偏差=真实值-预测值
6.R方 相关系数
- R^2 = SSR/SST = (SST-SSE)/SST = 1- SSE/SST 尽量接近1 表明模型越好.
- 偏差为0,4个系数求解,做了4组实验,刚好求解4个系数
- 调整R^2 = 1- ((nn-1)/(n-p))(1-r)
假设检验
假设x1的系数等于0,很大的概率支持a=0,所以删除ax1这一项.
7.三因子二水平全因子设计
- 截距+三个主项+二阶交互项+三阶交互项(忽略,认为不显著)
相关文章:

[创新工具和方法论]-01- DOE课程基础知识
文章目录 1.DOE实验设计的介绍1.1 什么是实验设计DOE?1.2 DOE的优势有哪些?1.3 如何开展DoE研究?步骤 2.DOE实验培训3.数据分析步骤4.实验的随机化5.偏差6.R方 相关系数假设检验 7.三因子二水平全因子设计 1.DOE实验设计的介绍 实验设计是一种安排实验和分析实验数…...
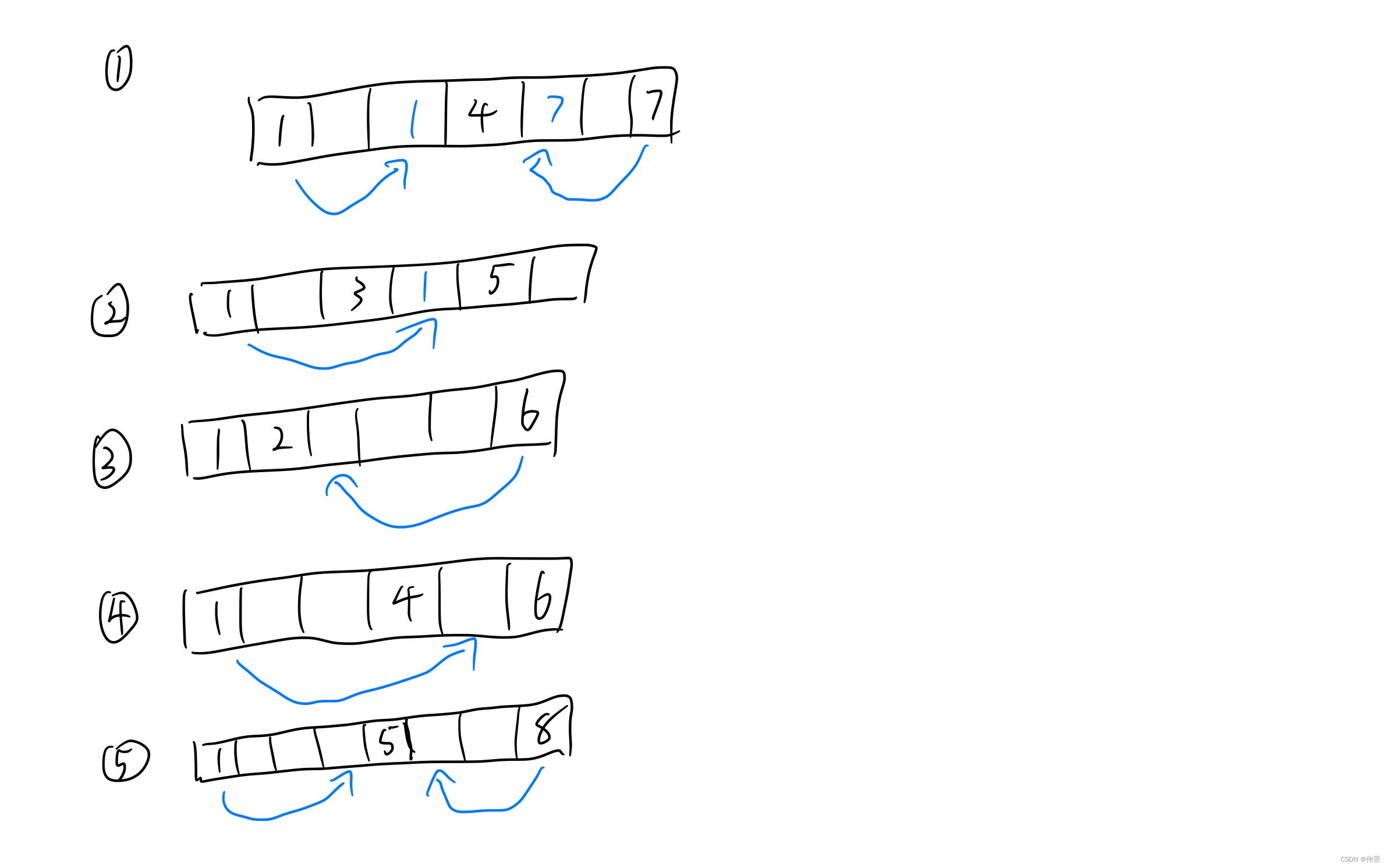
LeetCode-1033. 移动石子直到连续
题目链接 LeetCode-1033. 移动石子直到连续 题目描述 题解 题解一(Java) 作者:仲景 这题目挺难懂的,得画画图才能更好的理解 这也是LeetCode的尿性,习惯了,非得整这种别人看不懂的鸟语 你可以这样理解&a…...

JVM调优入门指南:掌握步骤、参数和场景
前言 作为Java开发者,我们经常需要优化应用的性能,其中JVM调优是非常重要的一部分。在本文中,我们将介绍JVM调优的一般步骤和方法,了解JVM调优参数,如堆大小、新生代比例、GC算法等参数的作用和配置方式,并…...

基于JSP+MySQL的跳蚤市场网站设计与开发
摘 要 在当今社会,网络信息已经不是什么很陌生的词汇,每天都在这个信息时代里生活着并且享受着它带来的与众不同。网络购物可以说是飞速发展的,这种购物方式逐渐的影响着人们的衣食住行。所以利用计算机实现 跳蚤市场网站设计与开发势在必行。本网站是一个校园的跳蚤市场网…...
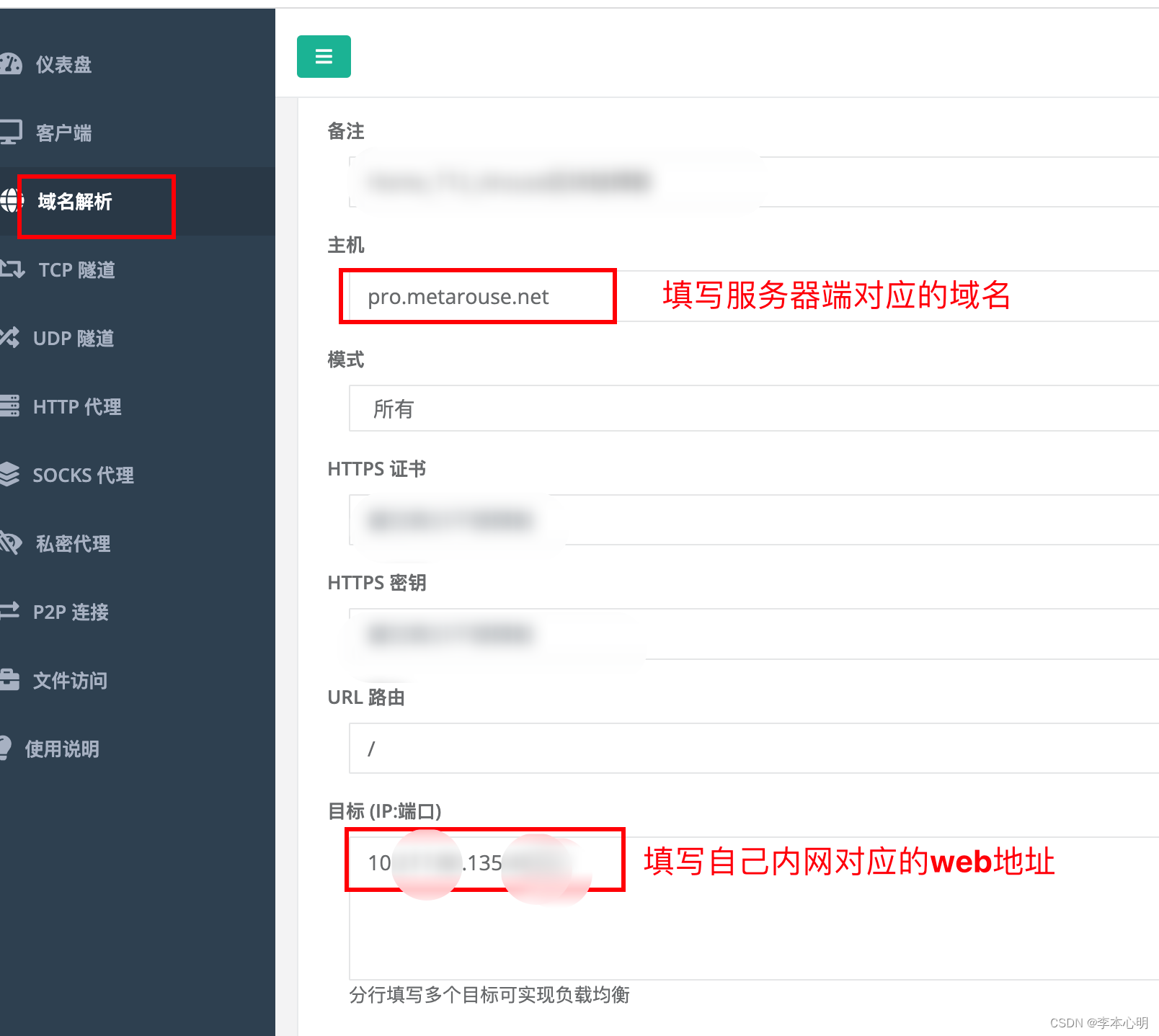
内网穿透NPS和宝塔Nginx配合使用,开启SSL访问本地局域网网络
并非为了教学,仅供自己记录,方便下次用。所以内容不会刻意花时间写的很细节详细。 1. 服务器NPS配置 NPS install安装后,配置文件会在其他位置,通过是 /etc/nps/nps.conf目录。 找到进行修改,主要修改的是http_proxy_p…...

ToLua框架
ToLua 是一个用于在 Unity 中为 Lua 提供 C# 语言绑定的框架。通过 ToLua,你可以方便地将 C# 代码暴露给 Lua 脚本,并在 Lua 脚本中调用 C# 类、方法和属性。 更新流程 原理:使用AssetBundle进行资源的更新,而由于lua运行时才编…...
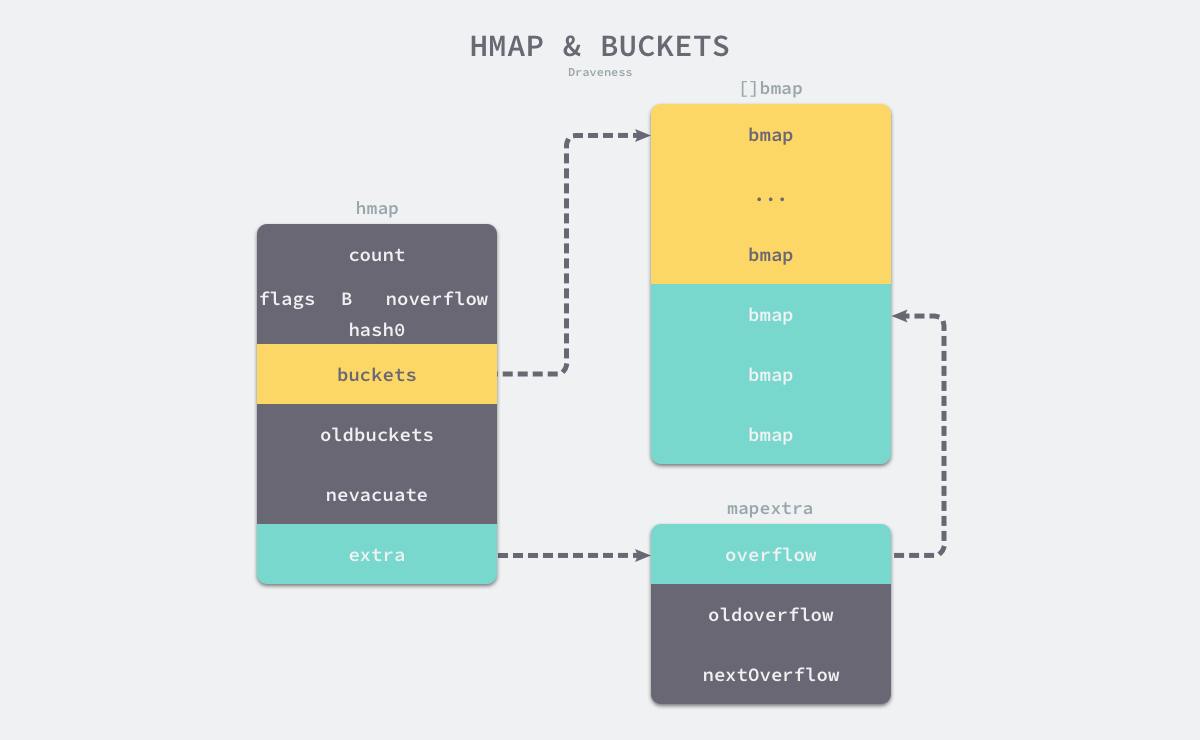
Golang-常见数据结构Map
Map map 是一种特殊的数据结构:一种元素对(pair)的无序集合,pair 的一个元素是 key,对应的另一个元素是 value,所以这个结构也称为关联数组或字典。这是一种快速寻找值的理想结构:给定 key&…...
基于空间矢量脉宽调制(SVPWM)的并网逆变器研究(Simulink)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

介绍tcpdump在centos中的使用方法
tcpdump是一款强大的命令行数据包分析器,支持多种过滤和抓包参数。下面将介绍tcpdump的常用抓包参数。当需要监控CentOS系统的网络流量或者进行网络故障排查时,可以使用tcpdump来捕获数据包并进行分析。 下面介绍在CentOS中使用tcpdump的方法࿱…...
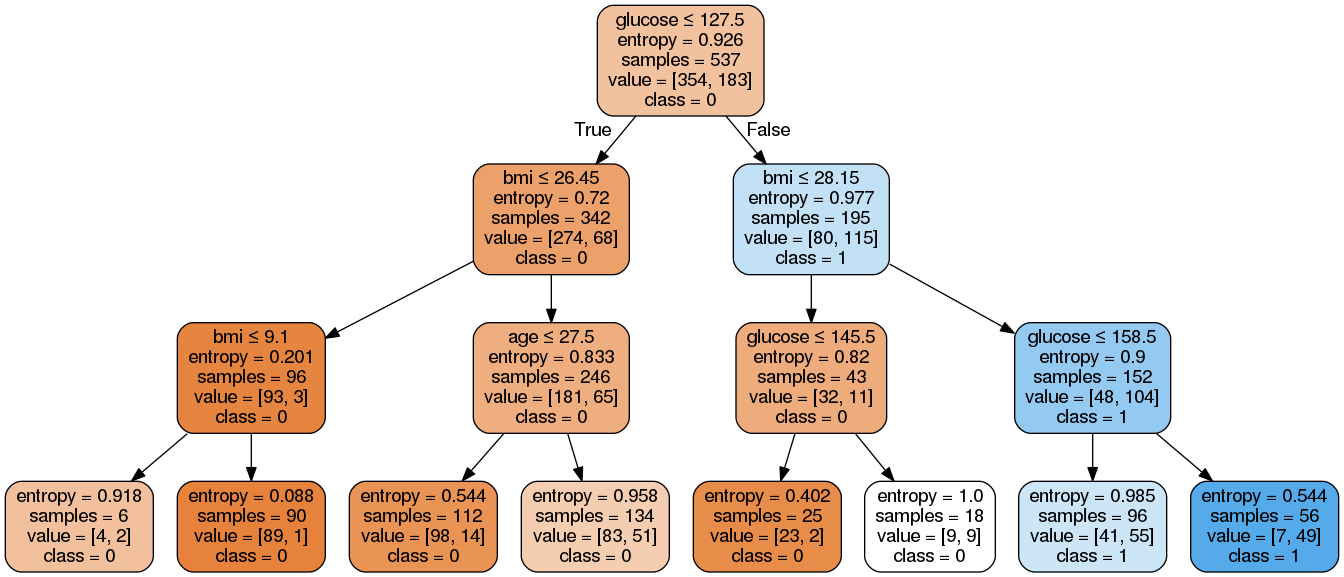
机器学习实战:Python基于DT决策树模型进行分类预测(六)
文章目录 1 前言1.1 决策树的介绍1.2 决策树的应用 2 Scikit-learn数据集演示2.1 导入函数2.2 导入数据2.3 建模2.4 评估模型2.5 可视化决策树2.6 优化模型2.7 可视化优化模型 3 讨论 1 前言 1.1 决策树的介绍 决策树(Decision Tree,DT)是一…...
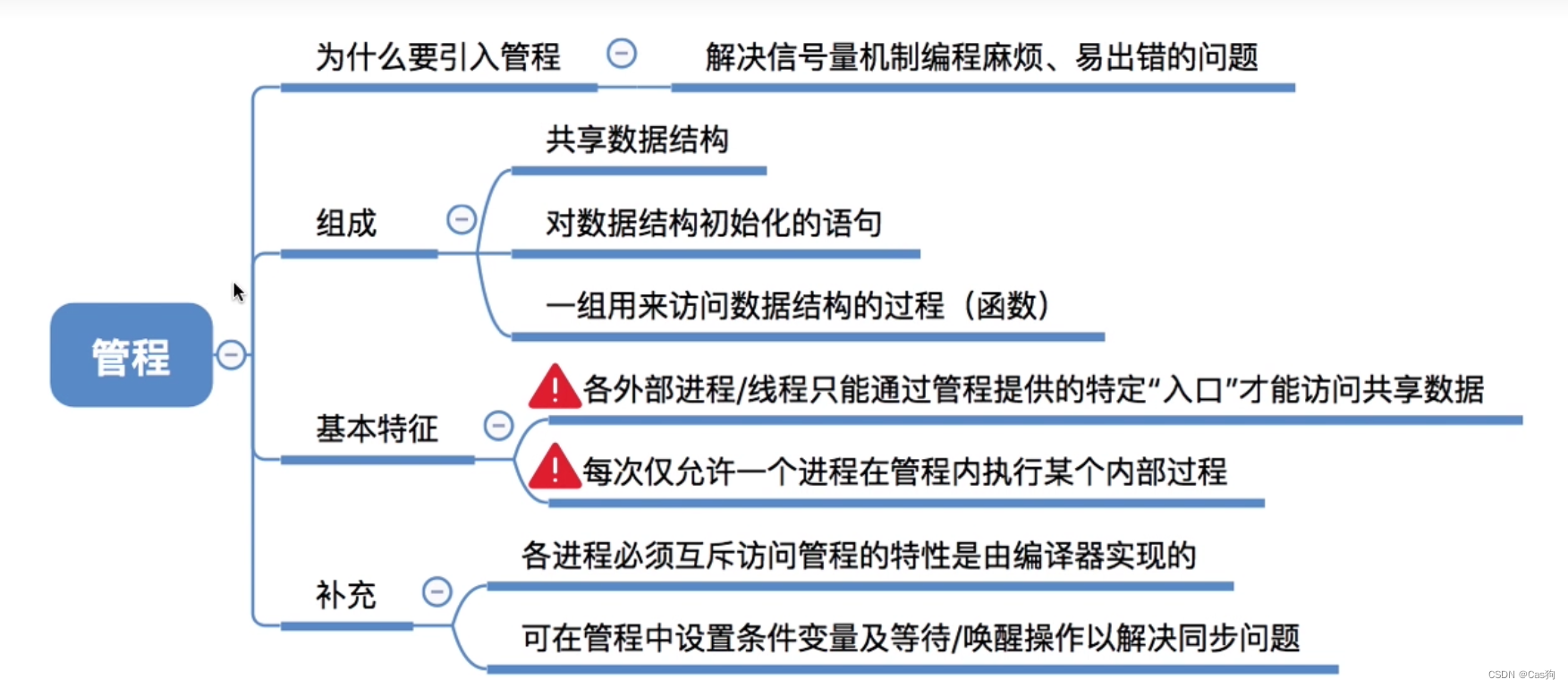
操作系统之进程同异步、互斥
引入 异步性是指,各并发执行的进程以各自独立的、不可预知的速度向前推进。 但是在一定的条件之下,需要进程按照一定的顺序去执行相关进程: 举例说明1: 举例说明2: 读进程和写进程并发地运行,由于并发必然导致异步性…...

你了解这2类神经性皮炎吗?常常预示着这5类疾病!
神经性皮炎属于慢性皮肤病,患者皮肤可出现局限性苔藓样变,同时伴有阵发性瘙痒。神经性皮炎易发生在颈部两侧和四肢伸侧,中年人是高发人群。到目前为止神经性皮炎病因还并不是很明确,不过一部分病人发病前常常出现精神神经方面异常…...
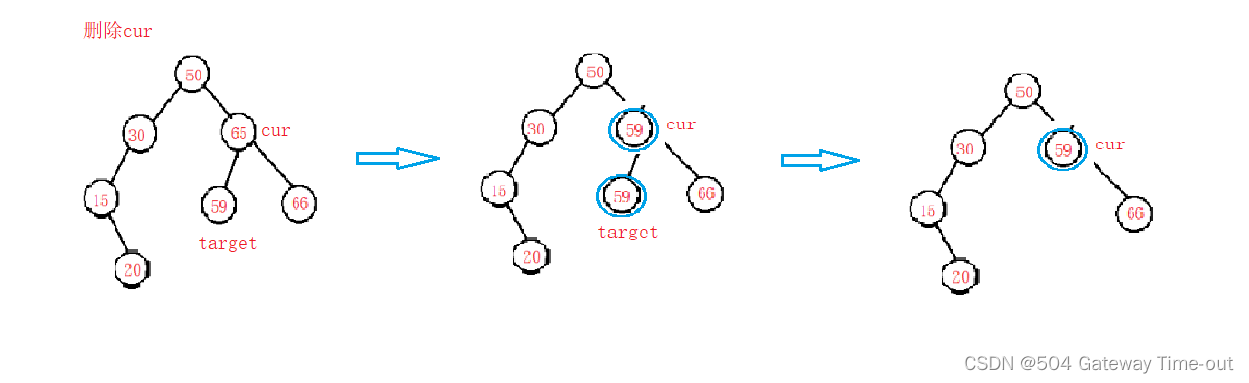
二叉搜索树【Java】
文章目录 二叉搜索树的性质二叉搜索树的操作遍历查找插入删除 二叉搜索树又称为二叉排序树,是一种具有一定性质的特殊的二叉树; 二叉搜索树的性质 若它的左子树不为空,则左子树上结点的值均小于根节点的值; 若它的右子树不为空&a…...

二叉树的遍历方式
文章目录 层序遍历——队列实现分析Java完整代码 先序遍历——中左右分析递归实现非递归实现——栈实现 中序遍历——左中右递归实现非递归实现——栈实现 后续遍历——左右中递归实现非递归实现——栈加标志指针实现 总结 层序遍历——队列实现 给你二叉树的根节点 root &…...
SpringCloud01
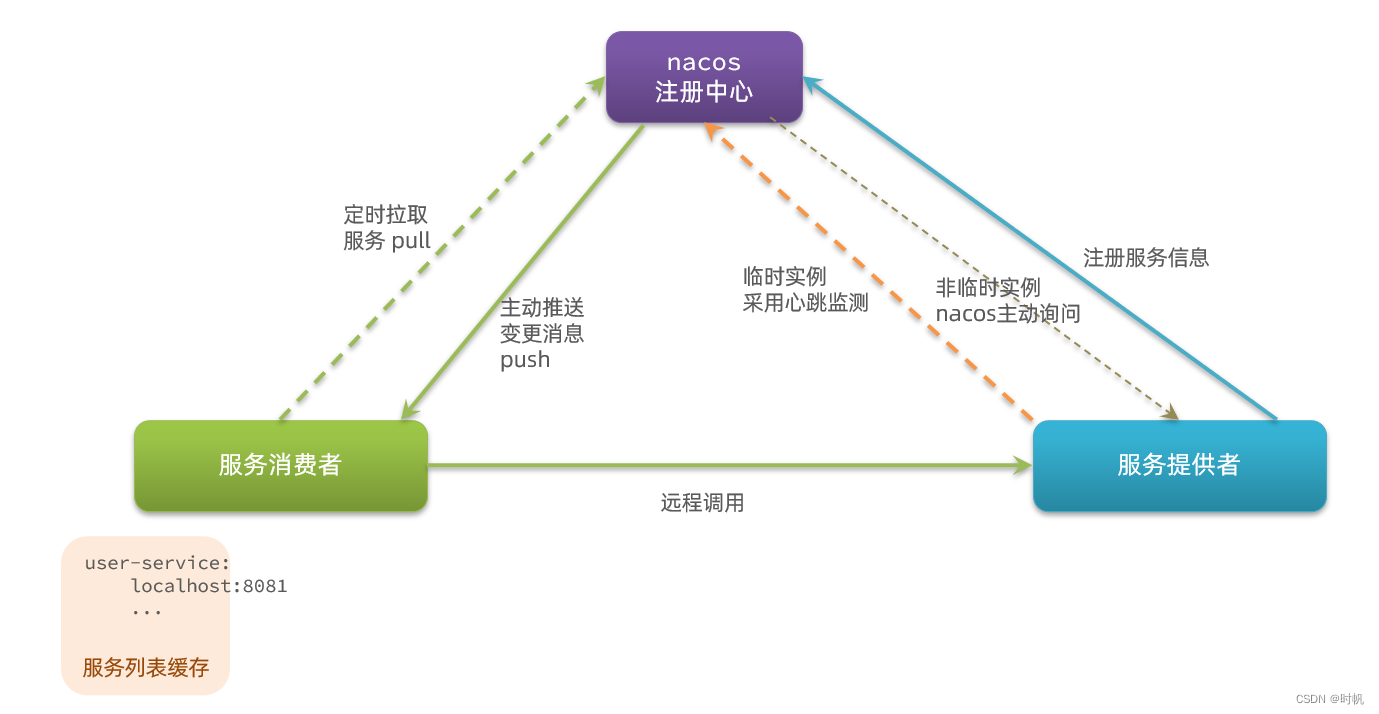
SpringCloud01 微服务入门案例 实现步骤 导入数据 实现远程调用 MapperScan("cn.itcast.order.mapper") SpringBootApplication public class OrderApplication {public static void main(String[] args) {SpringApplication.run(OrderApplication.class, args);}…...

SpringBoot整合Redis实现点赞、收藏功能
前言 点赞、收藏功能作为常见的社交功能,是众多Web应用中必不可少的功能之一。而redis作为一个基于内存的高性能key-value存储数据库,可以用来实现这些功能。 本文将介绍如何使用spring boot整合redis实现点赞、收藏功能,并提供前后端页面的…...

【Java入门合集】第一章Java概述
【Java入门合集】第一章Java概述 博主:命运之光 专栏:JAVA入门 学习目标 1.理解JVM、JRE、JDK的概念; 2.掌握Java开发环境的搭建,环境变量的配置; 3.掌握Java程序的编写、编译和运行; 4.学会编写第一个Java程序&#x…...

Android无线调试操作说明
1.首先通过手机机蓝牙将jackpal.androidterm-1.0.70.apk(终端模拟器)传的设备上安装 链接: https://pan.baidu.com/s/151SzEgsX0b_VTWowzfUrsA?pwdrn75 提取码: rn75 复制这段内容后打开百度网盘手机App,操作更方便哦 2.打开这个终端模拟器,输入以下命…...

什么是 Python ?聊一聊Python程序员找工作的六大技巧
最近我一直在思考换工作的事情。因此,这段时间我会看一些题目,看一些与面试相关的内容,以便更好地准备面试。我认为无论你处于什么阶段,面试中都会有技术面试环节。无论是初级职位还是高级职位,都需要通过技术面试来检…...

RabbitMQ 01 概述
什么是消息队列 进行大量的远程调用时,传统的Http方式容易造成阻塞,所以引入了消息队列的概念,即让消息排队,按照队列进行消费。 它能够将发送方发送的信息放入队列中,当新的消息入队时,会通知接收方进行处…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...
