LeetCode-1033. 移动石子直到连续
题目链接
LeetCode-1033. 移动石子直到连续
题目描述
题解
题解一(Java)
作者:@仲景
这题目挺难懂的,得画画图才能更好的理解
这也是LeetCode的尿性,习惯了,非得整这种别人看不懂的鸟语
你可以这样理解,给你一个假设长度为无穷的数组,其中有3个下标的位置赋值成了1,其余的都是0
问你,每次只能从头尾选择移动1次,最多多少次能让着3个1排到一起,最少多少次能让着3个1排到一起
这样也许会更好懂一些
先说最多的情况,最多的情况就是左边的1每次1步,一直移动到中间的1的前一个索引位置,右边的1每次1步,一直移动到中间的1的后一个索引位置
首先左右两个1的距离应该是c-a-1,因为中间还有一个b,所以还要-1,那么最多的公式就是c-a-2
那么最少情况呢,可以分成好多种
情况一:abc本身索引就是连续的,不需要动
情况二:ab连续或者bc连续,只需要把另外一个挪过来就可以了,移动1次
情况三:abc之间有空隙,但是空隙只有1个,那么随便挪动另外一个过来,最少也是移动1次
情况四:abc之间有空隙,但是空隙很多,所有a移动到b的前一个位置需要1次,c移动到b的后一个位置需要1次,那么最少也得2次
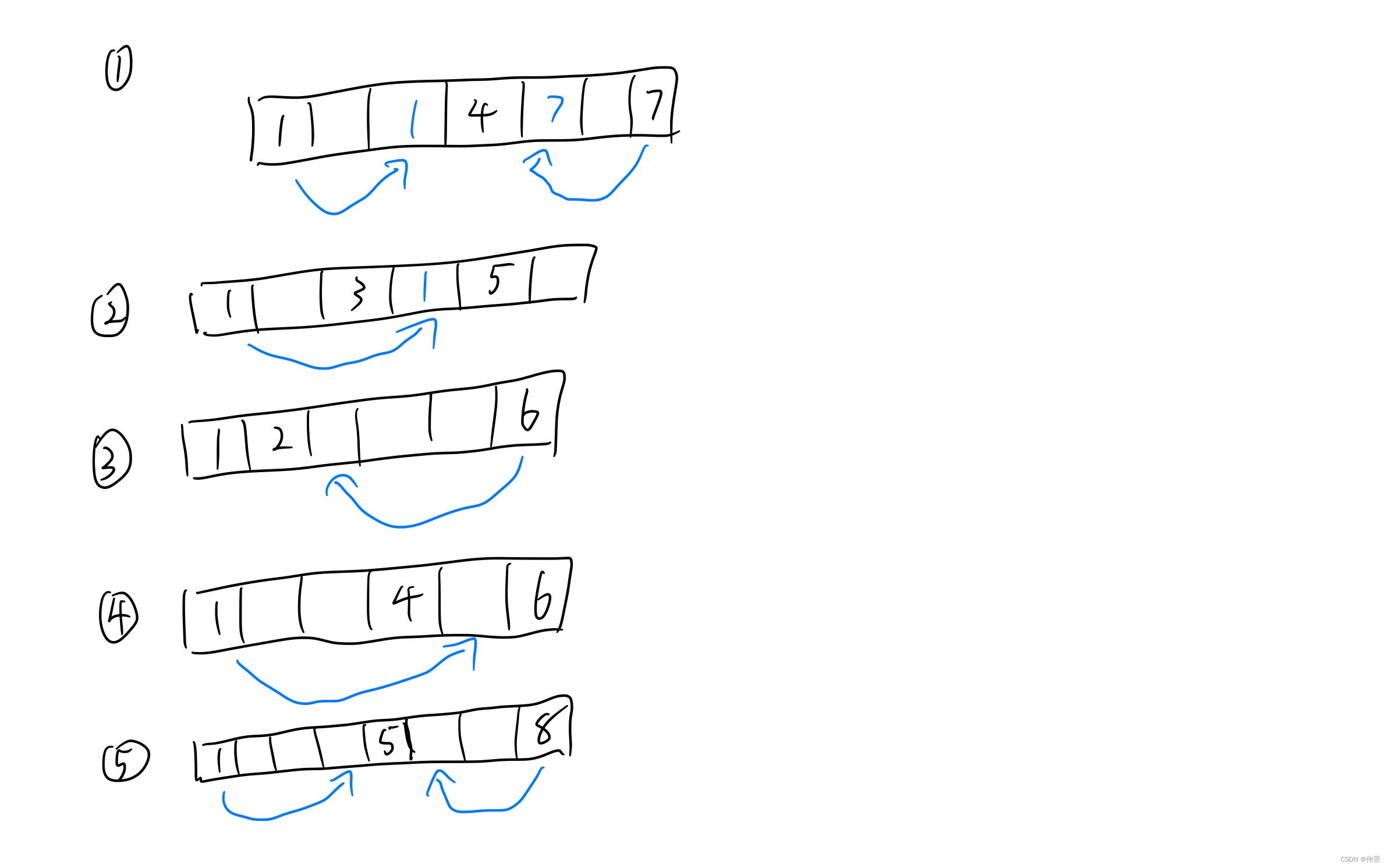
所有情况就已经讲完了,下面的图和情况1234不是一一对应的,只是用来证明情况1234的图
class Solution {public int[] numMovesStones(int a, int b, int c) {int[] arr = {a, b, c};Arrays.sort(arr);a = arr[0];b = arr[1];c = arr[2];int min = 0;// 如果c和a相差2,那abc就是连续的,不需要移动// 只有c和a之间有超过1个格子的时候才需要移动if (c - a > 2) {if (b - a <= 2 || c - b <= 2) {// 如果abc之中有任何两个元素紧挨着或者中间只有一个格子的时候,最少只需要1次就够了min = 1;} else {// 如果abc之中没有任何一个格子紧挨或者相差1个格子,那么最少需要2次min = 2;}}// 最多就是c-a-2return new int[]{min, c - a - 2};}
}
相关文章:
LeetCode-1033. 移动石子直到连续
题目链接 LeetCode-1033. 移动石子直到连续 题目描述 题解 题解一(Java) 作者:仲景 这题目挺难懂的,得画画图才能更好的理解 这也是LeetCode的尿性,习惯了,非得整这种别人看不懂的鸟语 你可以这样理解&a…...

JVM调优入门指南:掌握步骤、参数和场景
前言 作为Java开发者,我们经常需要优化应用的性能,其中JVM调优是非常重要的一部分。在本文中,我们将介绍JVM调优的一般步骤和方法,了解JVM调优参数,如堆大小、新生代比例、GC算法等参数的作用和配置方式,并…...

基于JSP+MySQL的跳蚤市场网站设计与开发
摘 要 在当今社会,网络信息已经不是什么很陌生的词汇,每天都在这个信息时代里生活着并且享受着它带来的与众不同。网络购物可以说是飞速发展的,这种购物方式逐渐的影响着人们的衣食住行。所以利用计算机实现 跳蚤市场网站设计与开发势在必行。本网站是一个校园的跳蚤市场网…...
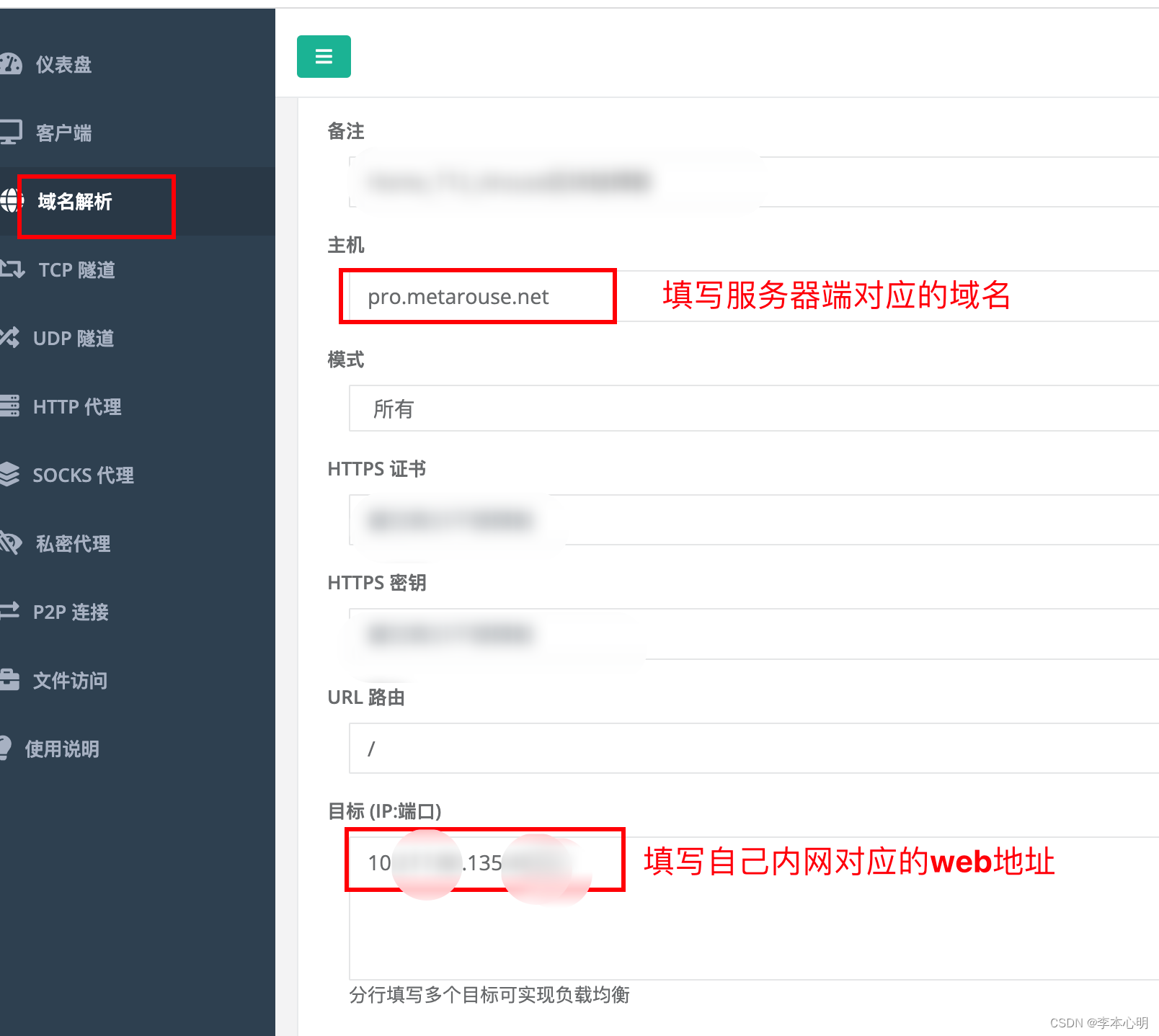
内网穿透NPS和宝塔Nginx配合使用,开启SSL访问本地局域网网络
并非为了教学,仅供自己记录,方便下次用。所以内容不会刻意花时间写的很细节详细。 1. 服务器NPS配置 NPS install安装后,配置文件会在其他位置,通过是 /etc/nps/nps.conf目录。 找到进行修改,主要修改的是http_proxy_p…...

ToLua框架
ToLua 是一个用于在 Unity 中为 Lua 提供 C# 语言绑定的框架。通过 ToLua,你可以方便地将 C# 代码暴露给 Lua 脚本,并在 Lua 脚本中调用 C# 类、方法和属性。 更新流程 原理:使用AssetBundle进行资源的更新,而由于lua运行时才编…...
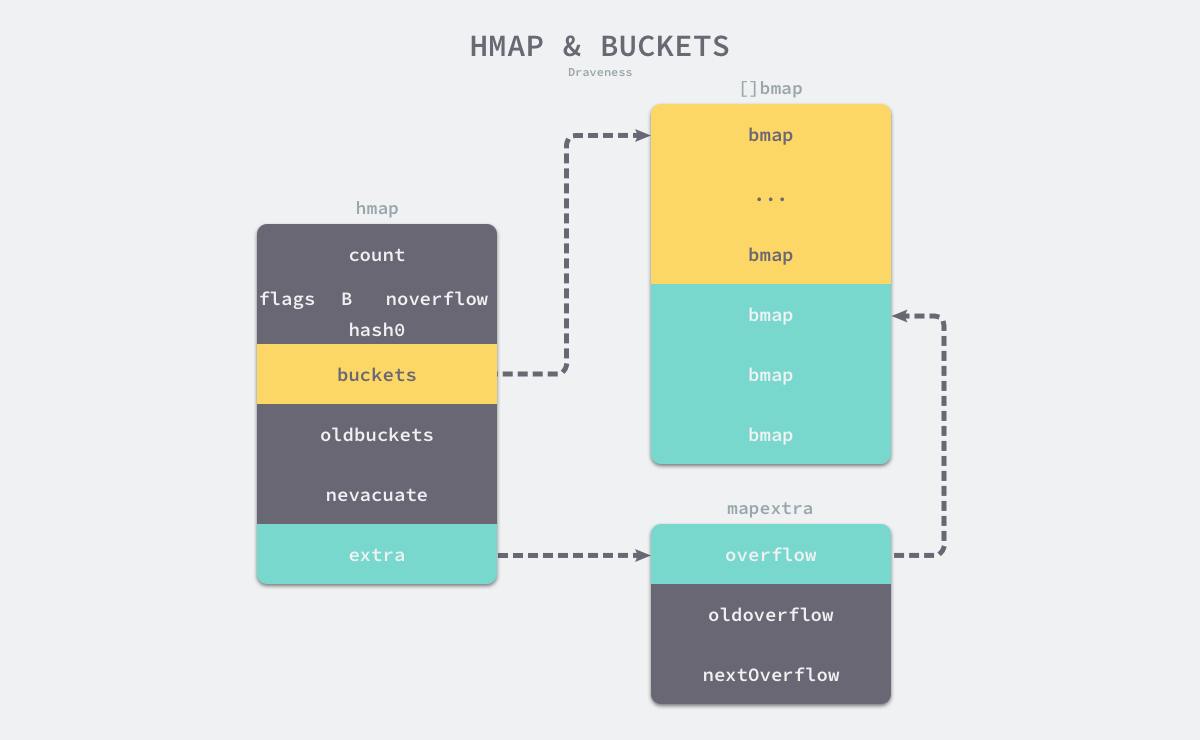
Golang-常见数据结构Map
Map map 是一种特殊的数据结构:一种元素对(pair)的无序集合,pair 的一个元素是 key,对应的另一个元素是 value,所以这个结构也称为关联数组或字典。这是一种快速寻找值的理想结构:给定 key&…...
基于空间矢量脉宽调制(SVPWM)的并网逆变器研究(Simulink)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

介绍tcpdump在centos中的使用方法
tcpdump是一款强大的命令行数据包分析器,支持多种过滤和抓包参数。下面将介绍tcpdump的常用抓包参数。当需要监控CentOS系统的网络流量或者进行网络故障排查时,可以使用tcpdump来捕获数据包并进行分析。 下面介绍在CentOS中使用tcpdump的方法࿱…...
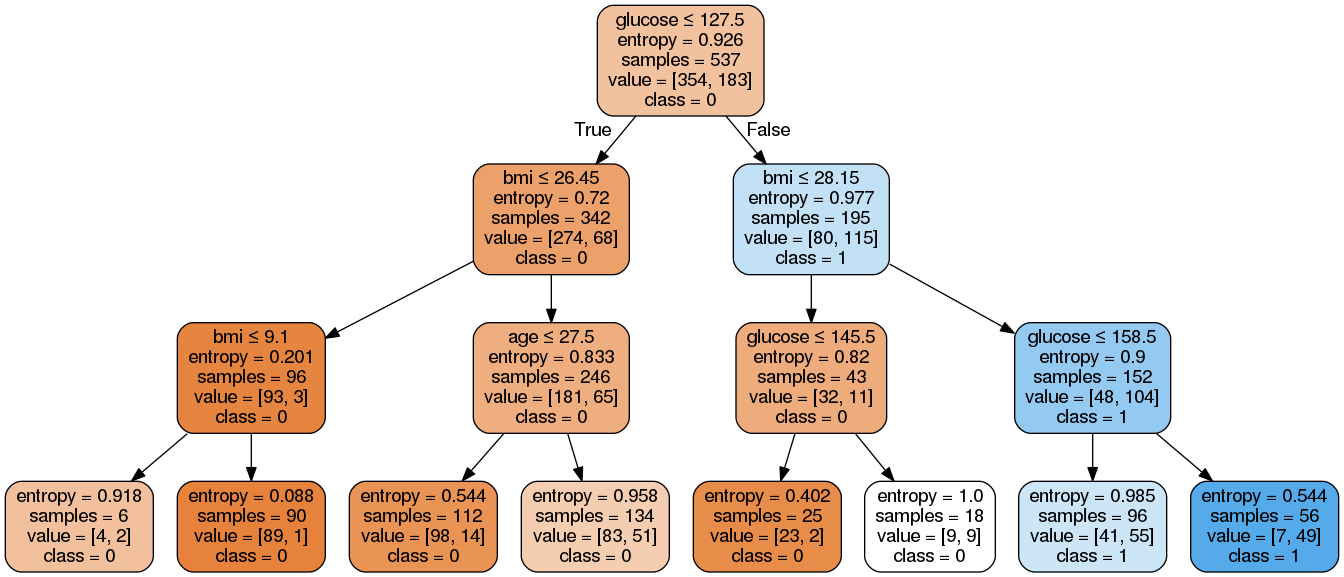
机器学习实战:Python基于DT决策树模型进行分类预测(六)
文章目录 1 前言1.1 决策树的介绍1.2 决策树的应用 2 Scikit-learn数据集演示2.1 导入函数2.2 导入数据2.3 建模2.4 评估模型2.5 可视化决策树2.6 优化模型2.7 可视化优化模型 3 讨论 1 前言 1.1 决策树的介绍 决策树(Decision Tree,DT)是一…...
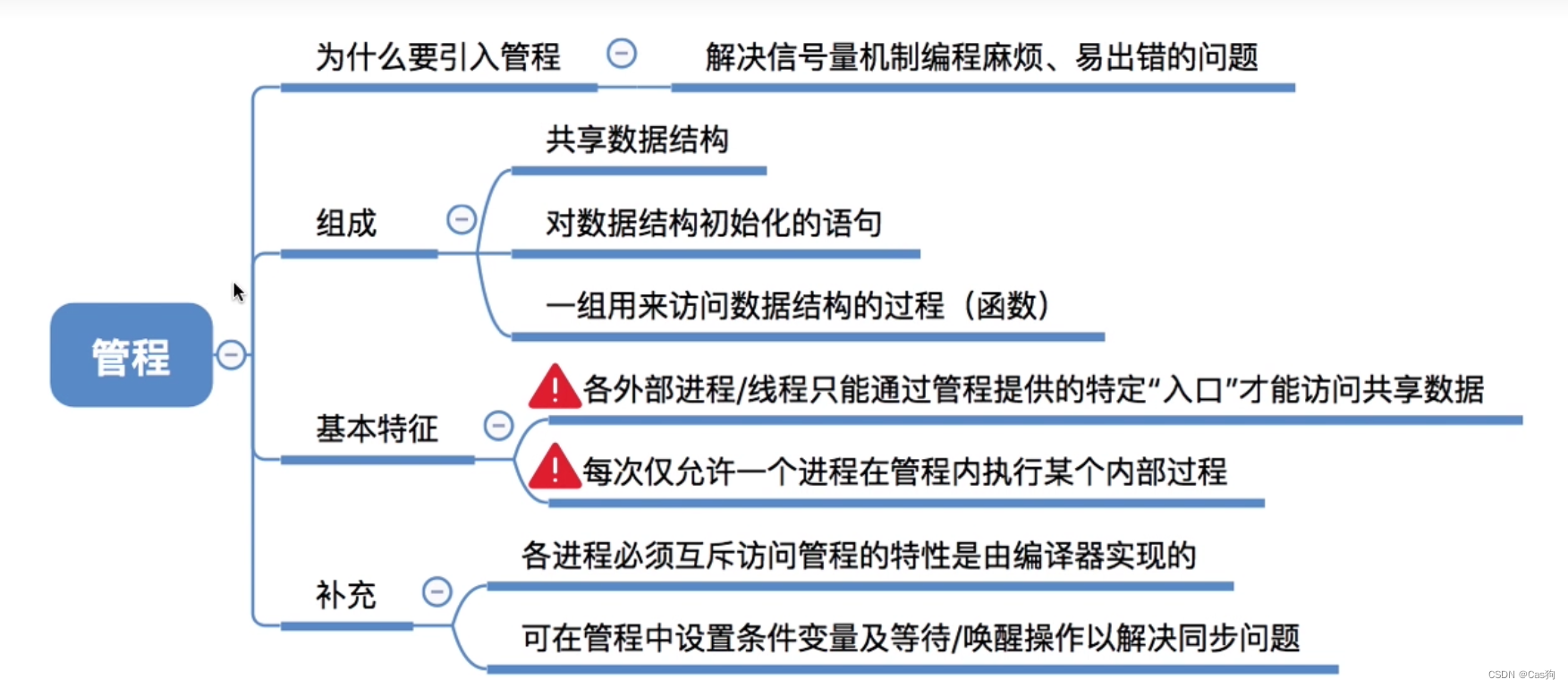
操作系统之进程同异步、互斥
引入 异步性是指,各并发执行的进程以各自独立的、不可预知的速度向前推进。 但是在一定的条件之下,需要进程按照一定的顺序去执行相关进程: 举例说明1: 举例说明2: 读进程和写进程并发地运行,由于并发必然导致异步性…...

你了解这2类神经性皮炎吗?常常预示着这5类疾病!
神经性皮炎属于慢性皮肤病,患者皮肤可出现局限性苔藓样变,同时伴有阵发性瘙痒。神经性皮炎易发生在颈部两侧和四肢伸侧,中年人是高发人群。到目前为止神经性皮炎病因还并不是很明确,不过一部分病人发病前常常出现精神神经方面异常…...
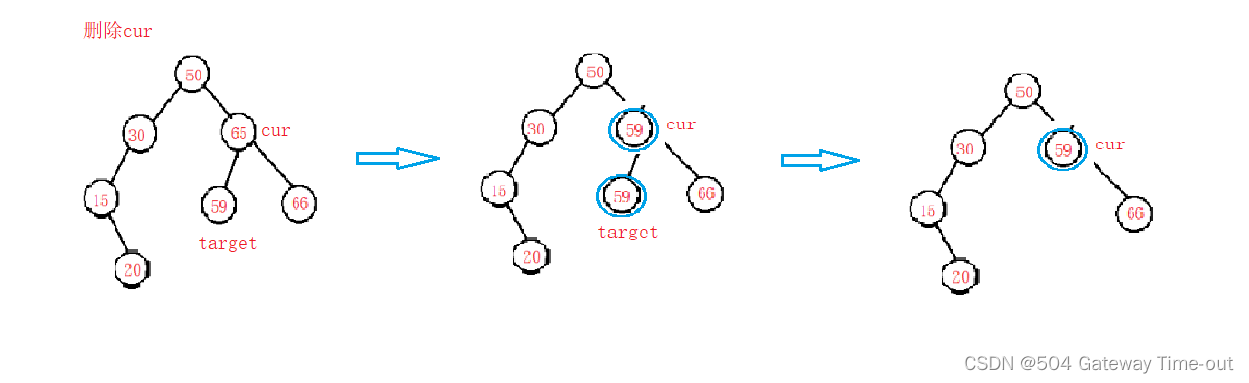
二叉搜索树【Java】
文章目录 二叉搜索树的性质二叉搜索树的操作遍历查找插入删除 二叉搜索树又称为二叉排序树,是一种具有一定性质的特殊的二叉树; 二叉搜索树的性质 若它的左子树不为空,则左子树上结点的值均小于根节点的值; 若它的右子树不为空&a…...

二叉树的遍历方式
文章目录 层序遍历——队列实现分析Java完整代码 先序遍历——中左右分析递归实现非递归实现——栈实现 中序遍历——左中右递归实现非递归实现——栈实现 后续遍历——左右中递归实现非递归实现——栈加标志指针实现 总结 层序遍历——队列实现 给你二叉树的根节点 root &…...
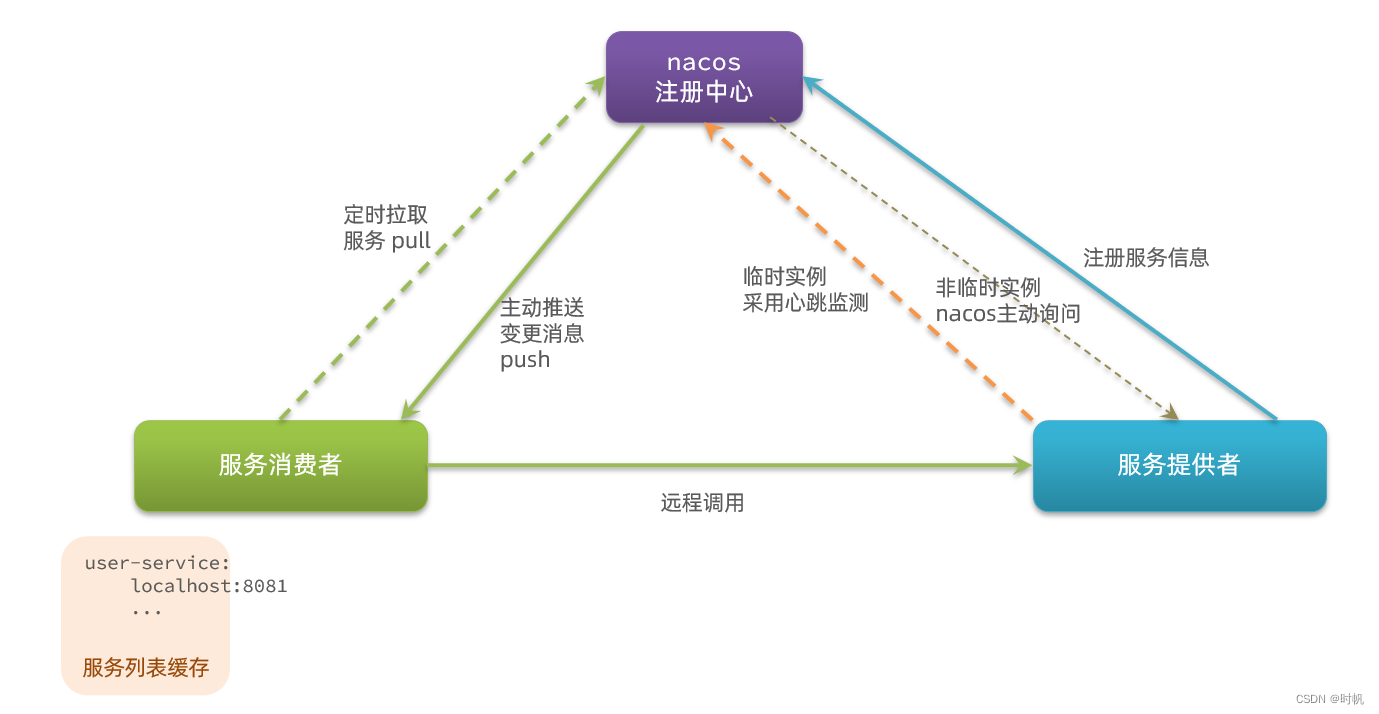
SpringCloud01
SpringCloud01 微服务入门案例 实现步骤 导入数据 实现远程调用 MapperScan("cn.itcast.order.mapper") SpringBootApplication public class OrderApplication {public static void main(String[] args) {SpringApplication.run(OrderApplication.class, args);}…...

SpringBoot整合Redis实现点赞、收藏功能
前言 点赞、收藏功能作为常见的社交功能,是众多Web应用中必不可少的功能之一。而redis作为一个基于内存的高性能key-value存储数据库,可以用来实现这些功能。 本文将介绍如何使用spring boot整合redis实现点赞、收藏功能,并提供前后端页面的…...

【Java入门合集】第一章Java概述
【Java入门合集】第一章Java概述 博主:命运之光 专栏:JAVA入门 学习目标 1.理解JVM、JRE、JDK的概念; 2.掌握Java开发环境的搭建,环境变量的配置; 3.掌握Java程序的编写、编译和运行; 4.学会编写第一个Java程序&#x…...

Android无线调试操作说明
1.首先通过手机机蓝牙将jackpal.androidterm-1.0.70.apk(终端模拟器)传的设备上安装 链接: https://pan.baidu.com/s/151SzEgsX0b_VTWowzfUrsA?pwdrn75 提取码: rn75 复制这段内容后打开百度网盘手机App,操作更方便哦 2.打开这个终端模拟器,输入以下命…...

什么是 Python ?聊一聊Python程序员找工作的六大技巧
最近我一直在思考换工作的事情。因此,这段时间我会看一些题目,看一些与面试相关的内容,以便更好地准备面试。我认为无论你处于什么阶段,面试中都会有技术面试环节。无论是初级职位还是高级职位,都需要通过技术面试来检…...

RabbitMQ 01 概述
什么是消息队列 进行大量的远程调用时,传统的Http方式容易造成阻塞,所以引入了消息队列的概念,即让消息排队,按照队列进行消费。 它能够将发送方发送的信息放入队列中,当新的消息入队时,会通知接收方进行处…...

面经|曹操出行供需策略运营
1.自我介绍 面试官表示看了简历之后,表示对专业能力比较放心。想了解下对于专业能力之外,关于其他方面的介绍。 2.策略运营,除了工具之外,还有哪些能力是需要具备的 回答:主要是从做项目的维度逻辑先去回答的。 分析思…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...
