代码随想录补打卡 746 使用最小花费爬楼梯
代码如下
func minCostClimbingStairs(cost []int) int {
dp := make([]int,len(cost)+1) //思路:设置一个花费数组dp,dp数组的长度等于之前的cost在加上1(1为楼顶元素)
dp[0] = 0
dp[1] = 0
for i := 2 ; i <= len(cost) ; i++ { //数组下标从2开始,因为dp数组长度为len(cost)+1,所以最后的下标为len(cost)
dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]) //和爬楼梯类似,可以爬一层也可以爬两层
}
return dp[len(cost)]
}
func min(a,b int) int {
if a < b {
return a
}else {
return b
}
}
相关文章:

代码随想录补打卡 746 使用最小花费爬楼梯
代码如下 func minCostClimbingStairs(cost []int) int { dp : make([]int,len(cost)1) //思路:设置一个花费数组dp,dp数组的长度等于之前的cost在加上1(1为楼顶元素) dp[0] 0 dp[1] 0 for i : 2 ; i < len(c…...

有理函数的不定积分习题
前置知识:有理函数的不定积分 习题 计算 ∫ x 3 1 x 4 − 3 x 3 3 x 2 − x d x \int \dfrac{x^31}{x^4-3x^33x^2-x}dx ∫x4−3x33x2−xx31dx 解: \qquad 将被积函数的分母因式分解得 x 4 − 3 x 3 3 x 2 − x x ( x − 1 ) 3 x^4-3x^33x^2-xx…...
PS滤镜插件-Nik Collection介绍
PS滤镜插件-Nik Collection介绍 什么是Nik CollectionNik Collection都包含什么? 什么是Nik Collection Nik Collection是一款PS滤镜插件套装,其包含了八款PS插件,功能涵盖修图、调色、降噪、胶片滤镜等方面。Nik Collection 作为很多摄影师…...
力扣刷题2023-05-04-1——题目:2614. 对角线上的质数
题目: 给你一个下标从 0 开始的二维整数数组 nums 。 返回位于 nums 至少一条 对角线 上的最大 质数 。如果任一对角线上均不存在质数,返回 0 。 注意: 如果某个整数大于 1 ,且不存在除 1 和自身之外的正整数因子,…...

【Java笔试强训 2】
🎉🎉🎉点进来你就是我的人了博主主页:🙈🙈🙈戳一戳,欢迎大佬指点! 欢迎志同道合的朋友一起加油喔🤺🤺🤺 目录 一、选择题 二、编程题 🔥排序子…...

术数基础背诵口诀整理
物象对应 五行方位天干神兽季节气候星宿生成数脏器木东甲乙青龙春风岁八肝火南丙丁朱雀夏热荧惑七心土中戊己?长夏湿镇五脾金西庚辛白虎秋燥太白九肺水北壬癸玄武冬寒辰六肾 口诀:东方甲乙青龙木,南方丙丁朱雀火,戊己勾陈腾蛇土&…...

Linux 基础语法 -2
如果我们以后再Linux当中 写了一些命名,导致程序我们不能进行操作了,如这个死循环: 他就会一直输出 "hello Linux" ,我们就使用 ctrl c 来终止因为程序或者指令异常,而导致我们无法进行指令输入ÿ…...
深度学习框架发展趋势
深度学习方法的发展是推动深度学习框架进步的最大动力,因此深度学习框架的功能和设计应顺应 算法和模型的发展趋势: 第一,易用性。深度学习领域仍处于快速发展期,参与者和学习者不断增加,新模型大量提出。因 此&#…...
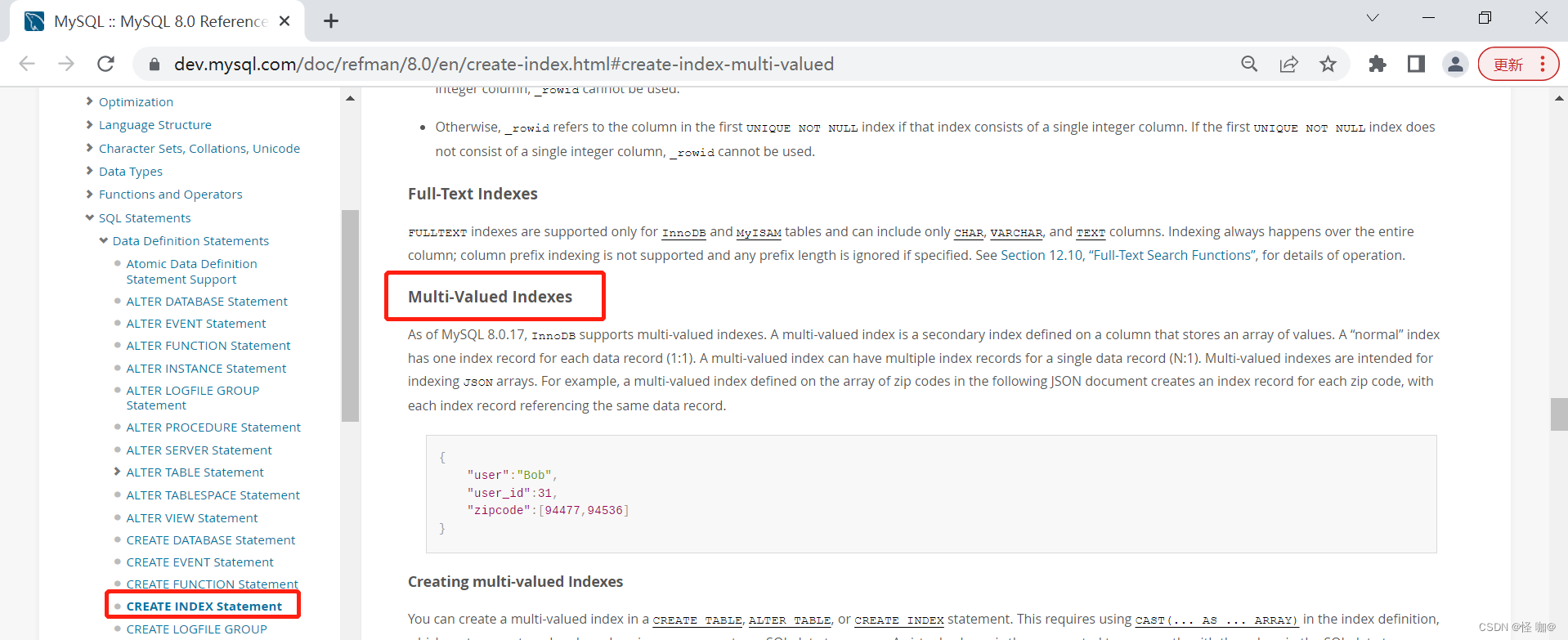
Mysql为json字段创建索引的两种方式
目录 一、前言二、通过虚拟列添加索引(Secondary Indexes and Generated Columns)三、多值索引(Using multi-valued Indexes)四、官网地址 一、前言 JSON 数据类型是在mysql5.7版本后新增的,同 TEXT,BLOB …...

cassandra数据库入门-4
插入数据 在表中创建数据 您可以使用命令 INSERT 将数据插入表中一行的列中。 下面给出了在表中创建数据的语法。 INSERT INTO <tablename> (<column1 name>, <column2 name>....) VALUES (<value1>, <value2>....) USING <option> 例子…...
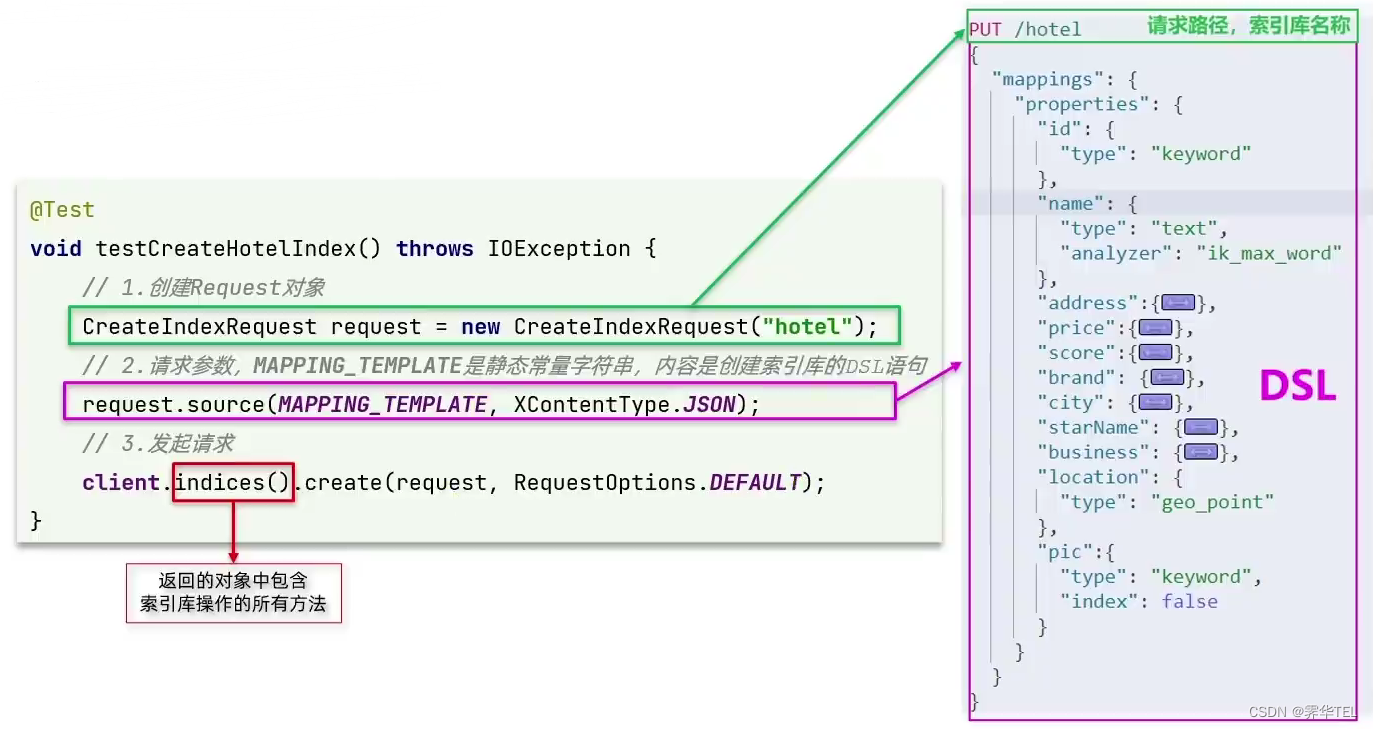
微服务学习——分布式搜索
初识elasticsearch 什么是elasticsearch elasticsearch是一款非常强大的开源搜索引擎,可以帮助我们从海量数据中快速找到需要的内容。 elasticsearch结合kibana、Logstash、Beats,也就是elastic stack(ELK)。被广泛应用在日志数据分析、实时监控等领域…...
ChatGPT根据销售数据、客户反馈、财务报告,自动生成报告,并根据不同利益方的需要和偏好进行调整?
该场景对应的关键词库(24个): 汇报对象身份(下属、跨部门平级、领导)、销售数据(销售额、销售量、销售渠道)、财务报告(营业收入、净利润、成本费用)、市场分析…...
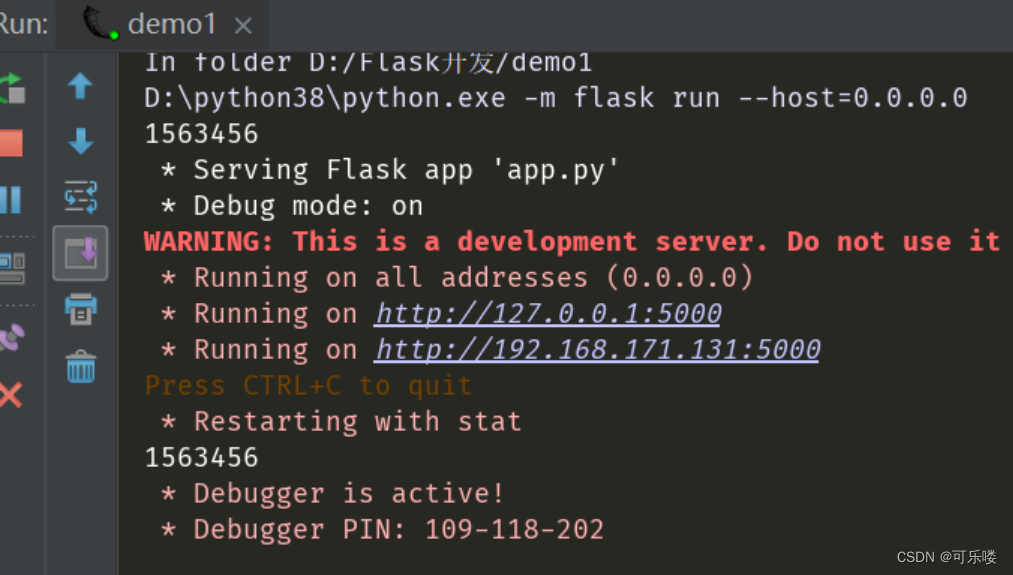
Flask开发之环境搭建
目录 1、安装flask 2、创建Flask工程 编辑 3、初始化效果 4、运行效果 5、设置Debug模式 6、设置Host 7、设置Port 8、在app.config中添加配置 1、安装flask 如果电脑上从没有安装过flask,则在命令行界面输入以下命令: pip install flask 如果电…...

Java集合框架与ArrayList、LinkedList的区别
文章目录 Java集合框架与ArrayList、LinkedList的区别集合框架ArrayList特点操作 LinkedList特点操作 区别代码实践注意事项 Java集合框架与ArrayList、LinkedList的区别 在Java中,集合框架是非常重要的一部分。集合框架提供了各种数据结构和算法,可以方…...

python-pandas库
目录 目录 目录 1.pandas库简介(https://www.gairuo.com/p/pandas-overview) 2.pandas库read_csv方法(https://zhuanlan.zhihu.com/p/340441922?utm_mediumsocial&utm_oi27819925045248) 1.pandas库简介(http…...
C++学习day--01 C生万物
1、C/C学习中遇到的问题: 1. 大部分初学者,学习 C/C 都是从入门到放弃。 C/C太难吗? 2. 90% 以上的初学者,学完 C/C 以后,考试完了,书看完了, 但还是不会做项目 是学的不够好吗࿱…...

链表及链表的常见操作和用js封装一个链表
最近在学数据结构和算法,正好将学习的东西记录下来,我是跟着一个b站博主学习的,是使用js来进行讲解的,待会也会在文章后面附上视频链接地址,大家想学习的可以去看看 本文主要讲解单向链表,双向链表后续也会…...

源码安装工具checkinstall使用
每当从源码包编译程序时,安装过程很愉快,但当你想删除时,就很费脑筋了,你可能要去找你当时编译的目录执行make unistall,当然更可能的是,你早就把源码包给删除了,对于强迫症来说,这显…...
离散数学集合论
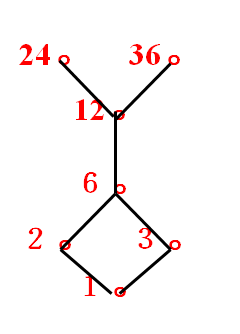
集合论 主要内容 集合基本概念 属于、包含幂集、空集文氏图等 集合的基本运算 并、交、补、差等 集合恒等式 集合运算的算律,恒等式的证明方法 集合的基本概念 集合的定义 集合没有明确的数学定义 理解:由离散个体构成的整体称为集合,…...

TypeScript 基础
类型注解 类型注解:约束变量的类型 示例代码: let age:number 18 说明:代码中的 :number 就是类型注解 解释:约定了类型,就只能给变量赋值该类型的值,否则,就会报错 错误演示:…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
