归一化处理(2023寒假每日一题 14)
在机器学习中,对数据进行归一化处理是一种常用的技术。
将数据从各种各样分布调整为平均值为 0 0 0、方差为 1 1 1 的标准分布,在很多情况下都可以有效地加速模型的训练。
这里假定需要处理的数据为 n n n 个整数 a 1 , a 2 , ⋯ , a n a_1,a_2,⋯,a_n a1,a2,⋯,an。
这组数据的平均值:

方差:

使用如下函数处理所有数据,得到的 n n n 个浮点数 f ( a 1 ) , f ( a 2 ) , ⋯ , f ( a n ) f(a_1),f(a_2),⋯,f(a_n) f(a1),f(a2),⋯,f(an) 即满足平均值为 0 0 0 且方差为 1 1 1:
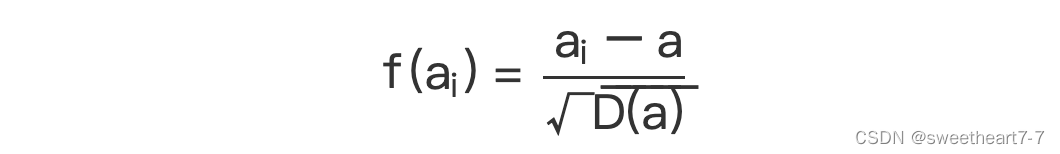
输入格式
第一行包含一个整数 n n n,表示待处理的整数个数。
第二行包含空格分隔的 n n n 个整数,依次表示 a 1 , a 2 , ⋯ , a n a_1,a_2,⋯,a_n a1,a2,⋯,an。
输出格式
输出共 n n n 行,每行一个浮点数,依次表示按上述方法归一化处理后的数据 f ( a 1 ) , f ( a 2 ) , ⋯ , f ( a n ) f(a_1),f(a_2),⋯,f(a_n) f(a1),f(a2),⋯,f(an) 。
如果你输出的每个浮点数与参考结果相比,均满足绝对误差不大于 1 0 − 4 10^{−4} 10−4,则该测试点满分,否则不得分。
数据范围
全部的测试数据保证 n , ∣ a i ∣ ≤ 1000 n,|a_i|≤1000 n,∣ai∣≤1000,其中 ∣ a i ∣ |a_i| ∣ai∣ 表示 a i a_i ai 的绝对值。且输入的 n n n 个整数 a 1 , a 2 , ⋯ , a n a_1,a_2,⋯,a_n a1,a2,⋯,an 满足:方差 D ( a ) ≥ 1 D(a)≥1 D(a)≥1。
输入样例:
7
-4 293 0 -22 12 654 1000
输出样例:
-0.7485510379073613
0.04504284674812264
-0.7378629047806881
-0.7966476369773906
-0.7057985054006686
1.0096468614303775
1.9341703768876082
样例解释
平均值: a ˉ ≈ 276.14285714285717 \bar a ≈ 276.14285714285717 aˉ≈276.14285714285717
方差: D ( a ) ≈ 140060.69387755104 D(a)≈140060.69387755104 D(a)≈140060.69387755104
标准差: D ( a ) ≈ 374.24683549437134 \sqrt{D(a)}≈374.24683549437134 D(a)≈374.24683549437134
#include<iostream>
#include<cmath>using namespace std;const int N = 1010;int n;
int a[N];int main(){scanf("%d", &n);int sum = 0;for(int i = 0; i < n; i++) scanf("%d", &a[i]), sum += a[i];double avg = sum * 1.0 / n;double sdiff = 0;for(int i = 0; i < n; i++) sdiff += (a[i] - avg) * (a[i] - avg);sdiff = sqrt(sdiff / n);for(int i = 0; i < n; i++) printf("%.16f\n", (a[i] - avg) / sdiff);return 0;
}
相关文章:
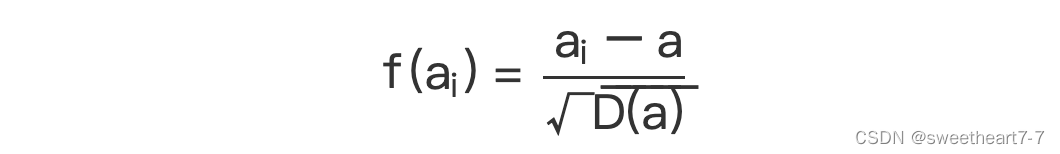
归一化处理(2023寒假每日一题 14)
在机器学习中,对数据进行归一化处理是一种常用的技术。 将数据从各种各样分布调整为平均值为 0 0 0、方差为 1 1 1 的标准分布,在很多情况下都可以有效地加速模型的训练。 这里假定需要处理的数据为 n n n 个整数 a 1 , a 2 , ⋯ , a n a_1,a_2,⋯…...

无公网IP,外网远程连接MySQL数据库
哈喽~大家好,这篇来看看无公网IP,外网远程连接MySQL数据库。 文章目录 前言1. 检查mysql安装状态2. 安装配置cpolar内网穿透3. 创建tcp隧道,映射3306端口4. 公网远程连接4.1 图形化界面4.2 使用命令行远程连接 5. 配置固定tcp端口地址5.1 保留…...
OJ刷题 第十四篇(递归较多)
23204 - 进制转换 时间限制 : 1 秒 内存限制 : 128 MB 将一个10进制数x(1 < x < 100,000,000)转换成m进制数(2< m < 16) 。分别用 ABCDEF表示10以上的数字。 输入 x m (1 < x < 100,000,000, 2< m < 16) 输出 m进制数 样例 输入 31 16 输出 1F 答…...
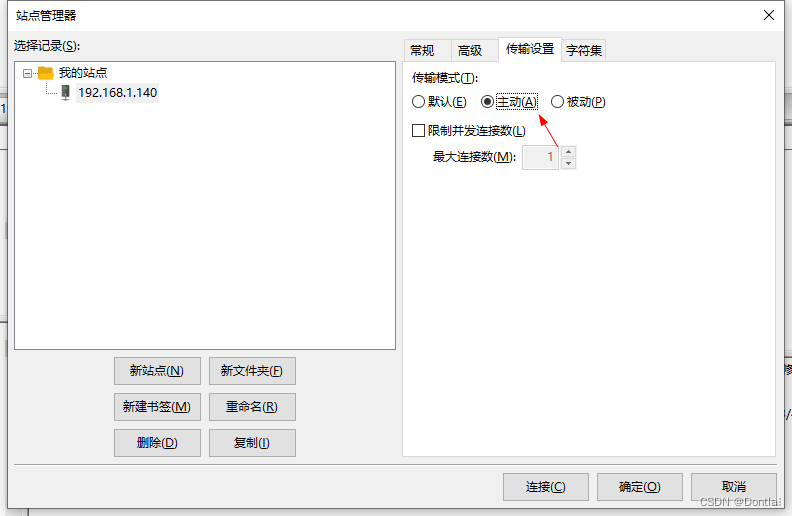
FileZilla读取目录列表失败(vsftpd被动模式passive mode部署不正确)
文章目录 现象问题原因解决方法临时解决(将默认连接方式改成主动模式)从根本解决(正确部署vsftpd的被动模式) 现象 用FileZilla快速连接vsftpd服务器时,提示读取目录列表失败 问题原因 是我vsftpd服务端的被动模式没…...
【Java面试八股文】数据库篇
导航: 【黑马Java笔记踩坑汇总】JavaSEJavaWebSSMSpringBoot瑞吉外卖SpringCloud黑马旅游谷粒商城学成在线MySQL高级篇设计模式牛客面试题 目录 请你说说MySQL索引,以及它们的好处和坏处 请你说说MySQL的索引是什么结构,为什么不用哈希表 请你说说数据库索引的底…...

Android Glide加载图片、网络监听、设置资源监听
再搞事情之前首先创建一个项目,就命名为GlideDemo吧。 一、项目配置 创建好之后,在app模块下build.gradle的dependencies闭包中添加如下依赖: //glide//glideimplementation com.github.bumptech.glide:glide:4.11.0annotationProcess…...

等保定级报告模版
等保定级怎么做_luozhonghua2000的博客-CSDN博客 上篇给大家说清楚了,等保定级怎么做,但在日常工作中,需要向上级或甲方输出定级报告,这篇我降弄个模版供大家参考。 信息系统安全等级保护定级报告 XX 平台系统描述 (一) 2023年5月,XX 正式上线,XX 隶属于深圳 XX 科技…...

计算机组成原理4.2.2汉明码
编码的最小距离 奇校验和偶校验 看1的个数是奇数 还是偶数 汉明码 汉明码的配置 根据不等式,确定增添几位,根据指数放置增添位 汉明码的检错 分不同检测小组 分组规则:哪位为’1‘就是哪组元素。 1号位为‘1’的都是第一组元素&#…...

JavaScript全解析——本地存储的概念、用法详解
本地存储概念: 就是浏览器给我们提供的可以让我们在浏览器上保存一些数据 常用的本地存储 localStorage sessionStorage localStorage 特点: 1.长期存储,除非手动删除否则会一直保存在浏览器中,清除缓存或者卸载浏览器也就没有了 2.可以跨页面通讯,…...
对象浅拷贝的5种方式
参考原文:浅拷贝的五种实现方式 - 掘金 (juejin.cn) 哈喽 大家好啊 最近发现自己对对象都不是很熟练,特别是涉及到一些复制,深浅拷贝的东西 1.Object.assign 首先 我们创建一个空对象obj1 然后创建一个对象obj2 用object.assign(目标对象,…...

Java每日一练(20230504)
目录 1. 位1的个数 🌟 2. 移除元素 🌟 3. 验证二叉搜索树 🌟🌟 🌟 每日一练刷题专栏 🌟 Golang每日一练 专栏 Python每日一练 专栏 C/C每日一练 专栏 Java每日一练 专栏 1. 位1的个数 编写一个…...

【深度学习】计算机视觉(13)——模型评价及结果记录
1 Tensorboard怎么解读? 因为意识到tensorboard的使用远不止画个图放个图片那么简单,所以这里总结一些关键知识的笔记。由于时间问题,我先学习目前使用最多的功能,大部分源码都包含summary的具体使用,基本不需要自己修…...

项目经理在项目中是什么角色?
有人说,项目经理就是一个求人的差事,你是在求人帮你做事。 有人说,项目经理就是一个与人扯皮的差事,你要不断的与开发、产品、测试等之间沟通、协调。 确实,在做项目的时候,有的人是为了完成功能&#x…...

【技术分享】防止根据IP查域名,防止源站IP泄露
有的人设置了禁止 IP 访问网站,但是别人用 https://ip 的形式,会跳到你服务器所绑定的一个域名网站上 直接通过 https://IP, 访问网站,会出现“您的连接不是私密连接”,然后点高级,会出现“继续前往 IP”,…...

Baumer工业相机堡盟相机如何使用偏振功能(偏振相机优点和行业应用)(C#)
项目场景: Baumer工业相机堡盟相机是一种高性能、高质量的工业相机,可用于各种应用场景,如物体检测、计数和识别、运动分析和图像处理。 Baumer的万兆网相机拥有出色的图像处理性能,可以实时传输高分辨率图像。此外࿰…...
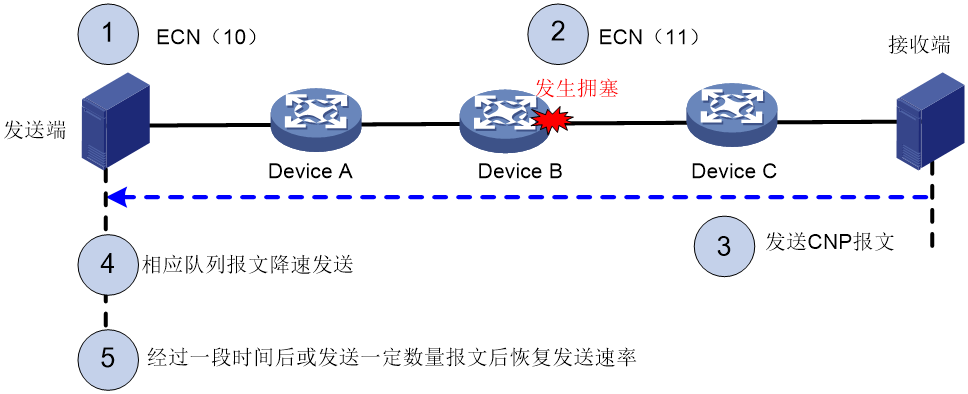
无损以太网与网络拥塞管理(PFC、ECN)
无损以太网 无损以太网(Lossless Ethernet)是一种专门用于数据中心网络的网络技术,旨在提供低延迟、高吞吐量和可靠性的传输服务。它是在传统以太网的基础上进行了扩展,引入了新的拥塞管理机制,以避免数据包丢失和网络…...

爬虫大全:从零开始学习爬虫的基础知识
爬虫是一种自动获取网站信息的技术,它可以帮助我们快速地抓取海量网站数据,进行统计分析、挖掘和展示。本文旨在为初学者详细介绍爬虫的基础知识,包括:爬虫原理、爬虫分类、网页结构分析、爬虫工具和技能、爬虫实践示范࿰…...

【Python】【进阶篇】21、Django Admin数据表可视化
目录 21、Django Admin数据表可视化1. 创建超级用户2. 将Model注册到管理后台1)在admin.py文件中声明 3. django_admin_log数据表 21、Django Admin数据表可视化 在《Django Admin后台管理系统》介绍过 Django 的后台管理系统是为了方便站点管理人员对数据表进行操作。Django …...

【MySQL约束】数据管理实用指南
1、数据库约束的认识 数据库约束的概念:数据库的约束是关系型数据库的一个重要的功能,它提供了一种“校验数据”合法性的机制,能够保证数据的“完整性”、“准确性”和“正确性” 数据库的约束: not null:不能存储 nul…...
2023年第二十届五一数学建模竞赛C题:“双碳”目标下低碳建筑研究-思路详解与代码答案
该题对于模型的考察难度较低,难度在于数据的搜集以及选取与处理。 这里推荐数据查询的网站:中国碳核算数据库(CEADs) https://www.ceads.net.cn/ 国家数据 国家数据data.stats.gov.cn/easyquery.htm?cnC01 以及各省市《统…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
