Java程序设计入门教程--案例:自由落体
程序模拟物体从10000米高空掉落后的反弹行为。
球体每落地一次,就会反弹至原高度的一半。按用户输入的弹跳次数,计算球体每次弹跳的高度。
实现过程:
(1)创建Scanner对象,设置参数:System.in。
(2)调用Scanner的nextInt方法获取用户输入的球体弹跳次数。
(1)创建球体高度整型变量,默认值:10000。
(2)创建for循环模拟反弹,循环边界:用户输入的弹跳次数。
(3)每次循环,球体高度 =球体高度 / 2;
(4)每次循环,判断球体的高度是否球体高度 / 2。等于0(球体落地):
1)如果已经落地,那么在控制台输出:"第" + N + "次反弹后,球体落地"(N为循环变量)。
2)如果未落地,那么继续计算高度。
package demo;import java.util.Scanner;public class JavaDemo
{public static void main(String[] args) {Scanner sc = new Scanner(System.in);int ci = sc.nextInt();int height = 10000;for(int i=1; i<=ci; i++){height = height / 2; // height/=2;if(height == 0){System.out.println("球体经过"+i+"次落地。");return;}}System.out.println("当前高度:"+height);}
}
效果如下:
相关文章:

Java程序设计入门教程--案例:自由落体
程序模拟物体从10000米高空掉落后的反弹行为。 球体每落地一次,就会反弹至原高度的一半。按用户输入的弹跳次数,计算球体每次弹跳的高度。 实现过程: 1. 新建项目; 2. 接收 用户输入的弹跳次数: (1&#…...

Qt音视频开发44-本地摄像头推流(支持分辨率/帧率等设置/实时性极高)
一、前言 本地摄像头推流和本地桌面推流类似,无非就是采集的设备源头换成了本地摄像头设备而不是桌面,其他代码完全一样。采集本地摄像头实时视频要注意的是如果设置分辨率和帧率,一定要是设备本身就支持的,如果不支持那就歇菜&a…...
SpringCloud学习(七)——统一网关Gateway
文章目录 1. 网关介绍2. 网关搭建2.1 引入依赖2.2 创建启动类2.3 编写配置2.4 测试 3. 路由断言工厂4. 路由过滤器4.1 过滤器配置4.2 全局过滤器4.3 过滤器执行顺序 5. 跨域问题处理 1. 网关介绍 到现在,我们可以使用Nacos对不同的微服务进行注册并管理配置文件&am…...

《花雕学AI》31:ChatGPT--用关键词/咒语/提示词Prompt激发AI绘画的无限创意!
你有没有想过用AI来画画?ChatGPT是一款基于GPT-3的聊天模式的AI绘画工具,它可以根据你输入的关键词/咒语/提示词Prompt来生成不同风格和主题的画作。Prompt是一些简短的文字,可以用来指导ChatGPT的创作过程。在这篇文章中,我将展示…...

计算机组成原理9控制单元的结构
9.1操作命令的分析 取值周期间址周期执行周期中断周期 取指周期数据流 PC存放下条指令的地址给MAR访问存储器相应单元,将数据取出来送给MDR寄存器,MDR取出来的内容送给IR指令寄存器,然后对指令进行译码,把指令的操作码部分取出…...

MySQL数据备份和恢复
MySQL数据备份和恢复 数据备份 mysqldump是MySQL数据库备份工具,可以备份MySQL数据库中的数据和结构,生成.sql文件,方便数据的迁移和恢复。 使用mysqldump工具前一定要配置环境变量 打开开始菜单,搜索“环境变量”。点击“编辑…...
)
数据结构与算法之链表: Leetcode 237. 删除链表中的节点 (Typescript版)
删除链表中的节点 https://leetcode.cn/problems/delete-node-in-a-linked-list/ 描述 有一个单链表的 head,我们想删除它其中的一个节点 node。 给你一个需要删除的节点 node 。你将 无法访问 第一个节点 head。 链表的所有值都是 唯一的,并且保证给…...

继承的相关介绍---C++
一、概念及定义 概念: 继承(inheritance)机制是面向对象程序设计使代码可以复用的最重要的手段,它允许程序员在保持原有类特性的基础上进行扩展,增加功能,这样产生新的类,称派生类。继承呈现了面向对象程序设计的层次结…...

Java多线程深入探讨
1. 线程与进程2. 创建和管理线程2.1. 继承Thread类2.2. 实现Runnable接口2.3 利用Callable、FutureTask接口实现。2.4 Thread的常用方法 3. 线程同步3.1. synchronized关键字3.1.1同步代码块:3.1.2 同步方法: 3.2. Lock接口 4. 线程间通信5. 线程池5.1 使…...
SpringCloud全面学习笔记之进阶篇
目录 前言微服务保护初识Sentinel雪崩问题及解决方案雪崩问题超时处理仓壁模式熔断降级流量控制总结 服务保护技术对比Sentinel介绍和安装微服务整合Sentinel 流量控制快速入门流控模式关联模式链路模式小结 流控效果warm up排队等待 热点参数限流全局参数限流热点参数限流案例…...
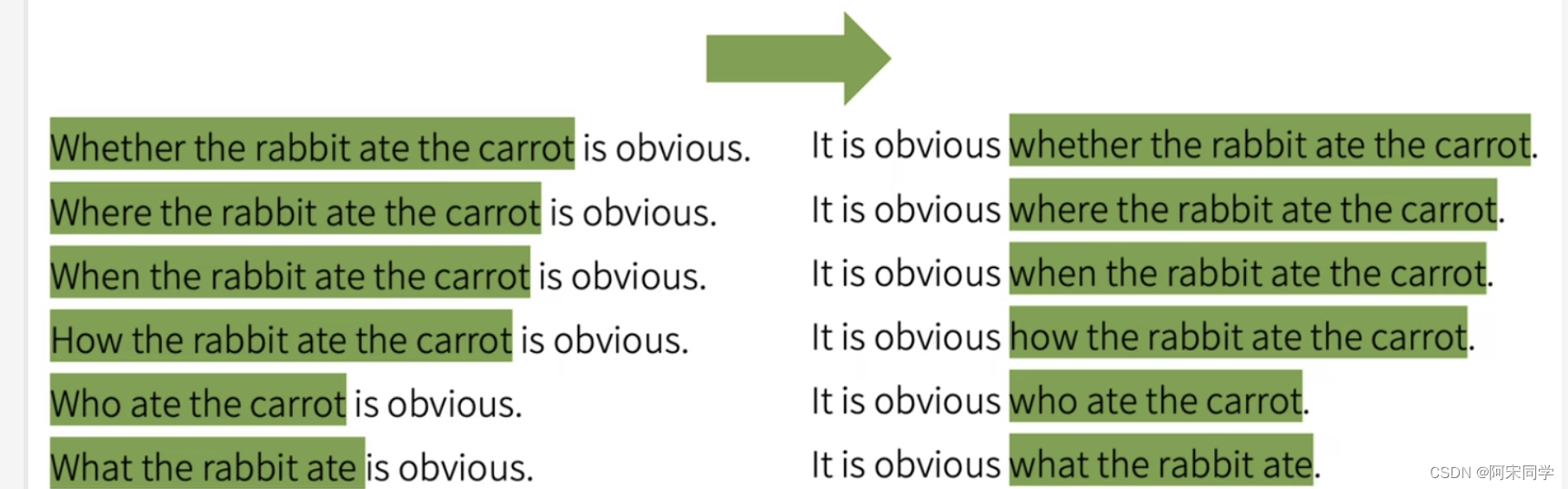
英语中主语从句的概念及其用法,例句(不断更新)
主语从句的原理 主语从句是一种充当整个句子主语的从句,主语从句构成的句子,是要以引导词开头的。它可以用名词性从属连词、关系代词或关系副词引导。主语从句通常位于谓语动词之前,用于表示动作、状态或事件的主体。 以下是一些常用的引导主…...
、子序列,字符串的子串、子序列)
数组的子数组(亚阵列)、子序列,字符串的子串、子序列
数组 子数组 一个或连续多个数组中的元素组成一个子数组 子数组最少包含一个元素 数组 {1, 2, 3} 的子数组是 {1}, {1, 2}, {1, 2, 3}, {2}, {2, 3}, 和 {3}. 子序列 子序列就是在原来序列中找出一部分组成的序列 子序列不一定连续 相对位置还是不变 但是ÿ…...
MySQL 知识:迁移数据目录到其他路径
一、系统环境 操作系统:Centos 7 已安装环境:MySQL 8.0.26 二、开始操作 2.1 关闭SELinux 为了提高 Linux 系统的安全性,在 Linux 上通常会使用 SELinux 或 AppArmor 实现强制访问控制(Mandatory Access Control MACÿ…...
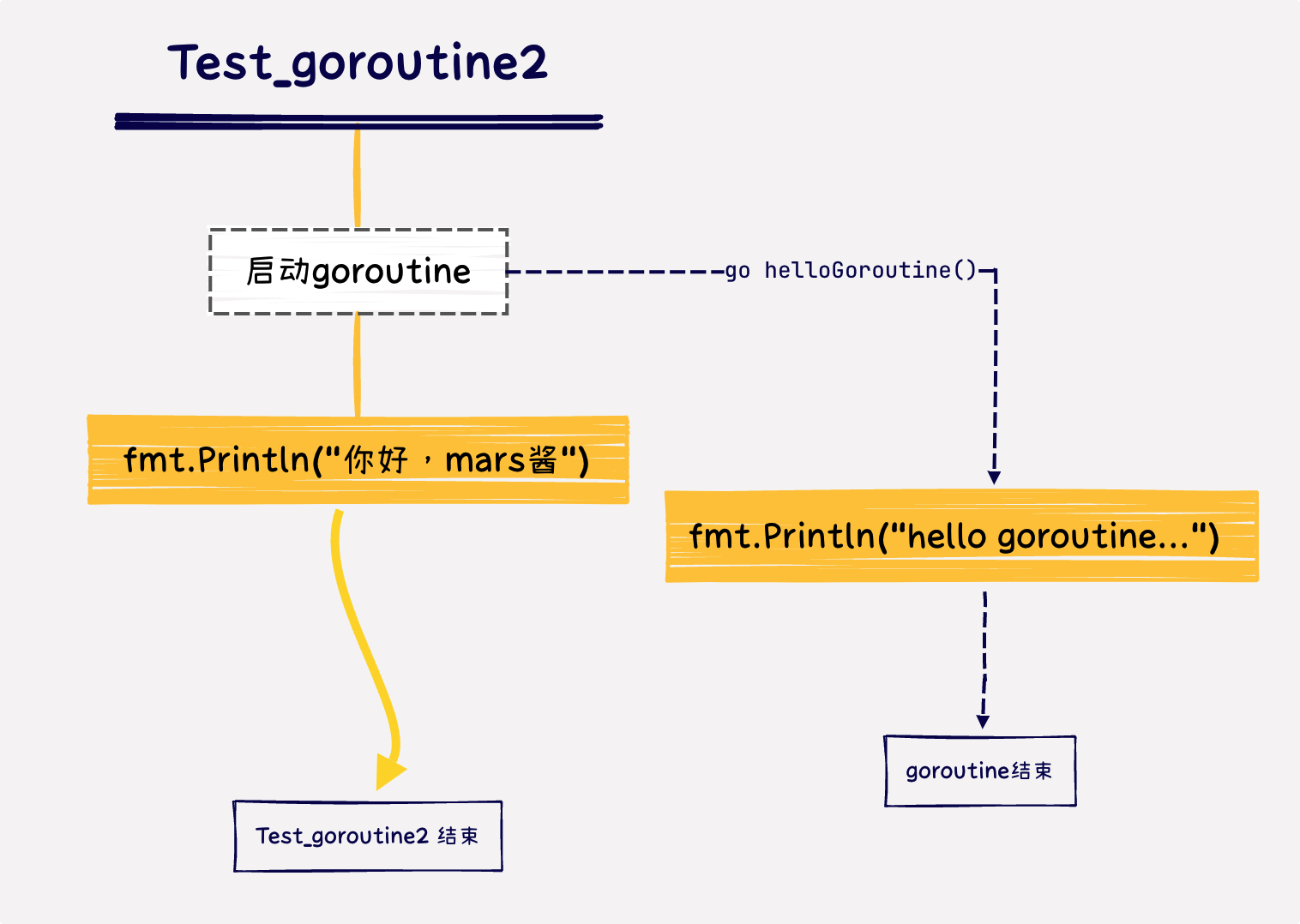
Go | 一分钟掌握Go | 8 - 并发
作者:Mars酱 声明:本文章由Mars酱编写,部分内容来源于网络,如有疑问请联系本人。 转载:欢迎转载,转载前先请联系我! 前言 当今编程界,一个好的编译型语言如果不支持并发,…...

【滤波】多元高斯
本文主要翻译自rlabbe/Kalman-and-Bayesian-Filters-in-Python的第5章节05-Multivariate-Gaussians(多元高斯)。 %matplotlib inline#format the book import book_format book_format.set_style()简介 上一篇文章中的技术非常强大,但它们只…...
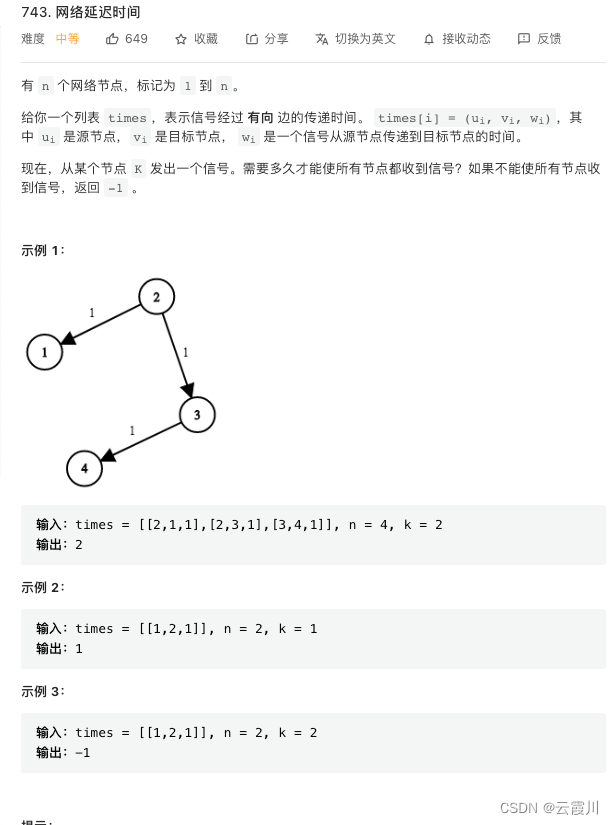
单源最短路问题
全部代码 全部代码在github acwing 上 正在更新 https://github.com/stolendance/acwing 图论 欢迎大家star与fork 单源最短路问题 先用spfa算法 不行再换其他的 spfa-超级万能 说不定比dijsktra还快 dis[] 代表第k到某一点的最短距离 queue 代表刚被更新的点 它有可能更…...

Security方法注解权限控制过程及自定义权限表达式
文章目录 使用内置的权限表达式PreAuthorizePermissionEvaluator 自定义权限表达式SysMethodSecurityExpressionHandler源码流程 SysMethodSecurityExpressionRoot 使用内置的权限表达式 PreAuthorize 这个用来判断超级管理员的话,还得在表达式上加上或 Permissi…...

vue 省市县三级联动
1、 <template><div>所在省<el-select popper-class"eloption" :popper-append-to-body"true"change"getShiList(obj.province)" v-model"obj.province" placeholder"请选择所在省" clearableclear"re…...

ChatGPT实现编程语言转换
编程语言转换 对于程序员来说,往往有一类工作,是需要将一部分业务逻辑实现从服务端转移到客户端,或者从客户端转移到服务端。这类工作,通常需要将一种编程语言的代码转换成另一种编程语言的代码,这就需要承担这项工作…...
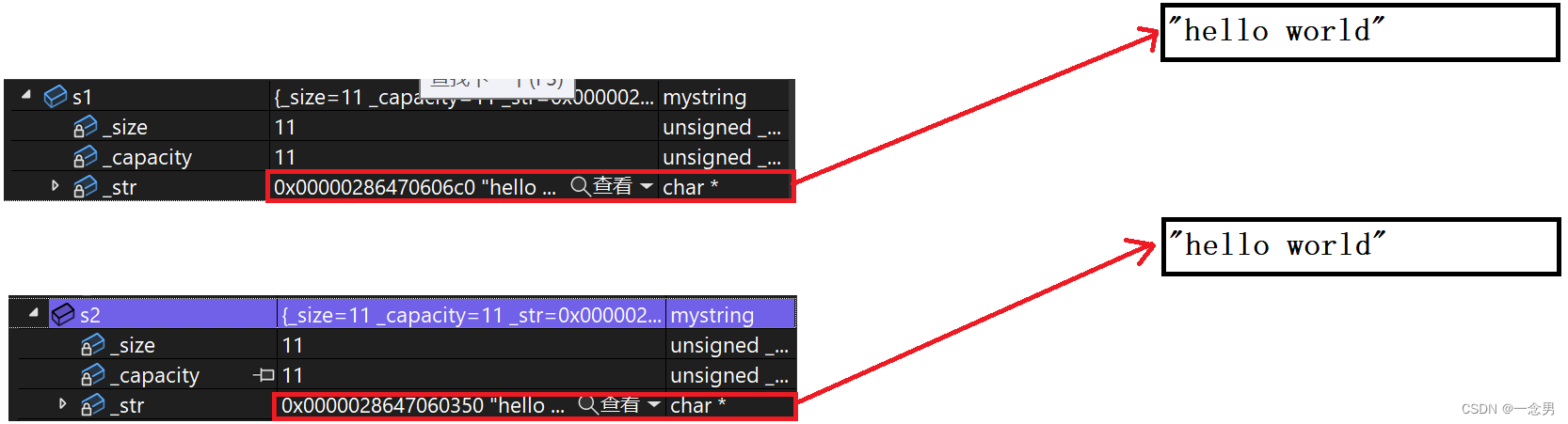
浅拷贝和深拷贝
浅拷贝: 定义:浅拷贝(Shallow Copy)是一种简单的对象复制方式,将一个对象的数据成员直接复制给另一个对象(通常是通过默认的复制构造函数或赋值运算符实现),这些数据成员可以是基本…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...

GraphRAG优化新思路-开源的ROGRAG框架
目前的如微软开源的GraphRAG的工作流程都较为复杂,难以孤立地评估各个组件的贡献,传统的检索方法在处理复杂推理任务时可能不够有效,特别是在需要理解实体间关系或多跳知识的情况下。先说结论,看完后感觉这个框架性能上不会比Grap…...

高保真组件库:开关
一:制作关状态 拖入一个矩形作为关闭的底色:44 x 22,填充灰色CCCCCC,圆角23,边框宽度0,文本为”关“,右对齐,边距2,2,6,2,文本颜色白色FFFFFF。 拖拽一个椭圆,尺寸18 x 18,边框为0。3. 全选转为动态面板状态1命名为”关“。 二:制作开状态 复制关状态并命名为”开…...
