C++-----动态规划
目录
一、动态规划的基本思想
二、设计动态规划法的步骤
三、动态规划问题的特征
4.1 矩阵连乘积问题
4.1.1 分析最优解的结构
4.1.2 建立递归关系
4.1.3 计算最优值
4.1.3 计算最优值
4.1.3 构造最优解
4.2 动态规划算法的基本要素
4.2.1 最优子结构
4.2.2 重叠子问题
算法4.3 计算矩阵连乘积的递归算法
4.1.3 备忘录方法
算法4.4计算矩阵连乘积的备忘录算法
编辑
4.3 最长公共子序列
4.3.2 子问题的递归结构
4.3.3 计算最优值
4.4 最大子段和
一、动态规划的基本思想
- 动态规划算法通常用于求解具有某种最优性质的问题。
- 在这类问题中,可能会有许多可行解。
- 基本思想是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
- 如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。
- 这就是动态规划法的基本思路。
二、设计动态规划法的步骤
三、动态规划问题的特征
- 动态规划算法的有效性依赖于问题本身所具有的两个重要性质:
- 当问题的最优解包含了其子问题的最优解时,称该问题具有最优子结构性质。
- 在用递归算法自顶向下解问题时,每次产生的子问题并不总是新问题,有些子问题被反复计算多次。动态规划算法正是利用了这种子问题的重叠性质,对每一个子问题只解一次,而后将其解保存在一个表格中,在以后尽可能多地利用这些子问题的解。
4.1 矩阵连乘积问题
- m×n矩阵A与n×p矩阵B相乘需耗费 的时间。
- 我们把mnp作为两个矩阵相乘所需时间的测量值。
- 现在假定要计算三个矩阵A、B和C的乘积,有两种方式计算此乘积。
- 尽管这两种不同的计算顺序所得的结果相同,但时间消耗会有很大的差距。


- 定义:给定n个矩阵{A1,A2,…,An},其中Ai与Ai+1是可乘的,i=1,2,…n-1。考察这n个矩阵的连乘积A1A2…An。
- 由于矩阵乘法满足结合律,所以计算矩阵的连乘可以有许多不同的计算次序。
- 这种计算次序可以用加括号的方式来确定。
- 若一个矩阵连乘积的计算次序完全确定,也就是说该连乘积已完全加括号,则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积
- 完全加括号的矩阵连乘积可递归地定义为:
- 设有四个矩阵A, B, C, D,总共有五种完全加括号的方式:
(A((BC)D))
(A(B(CD)))
((AB)(CD))
(((AB)C)D)
((A(BC)D))
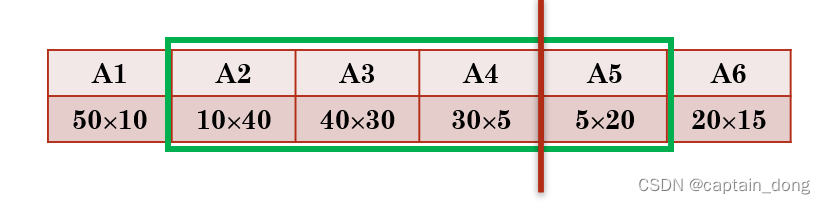
- 设有四个矩阵A, B, C, D,它们的维数分别是:
A=50×10, B=10×40, C=40×30, D=30×5
- 矩阵A和B可乘的条件: 矩阵A的列数等于矩阵B的行数。
- 设A是p×q的矩阵, B是q×r的矩阵, 乘积是p×r的矩阵;
- 上述5种完全加括号方式的计算工作量为:
(A((BC)D)), (A(B(CD))), ((AB)(CD)), (((AB)C)D), ((A(BC)D))
16000, 10500, 36000, 87500, 34500
BC: 10×40×30 = 12000,
(BC)D: 10×30×5 = 1500,
(A((BC)D)): 50×10×5 = 2500
- 给定n个矩阵{A1,A2,…,An},其中Ai与Ai+1是可乘的,i=1,2…,n-1。如何确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少?
- 穷举法:列举出所有可能的计算次序,并计算出每一种计算次序相应需要的数乘次数,从中找出一种数乘次数最少的计算次序。

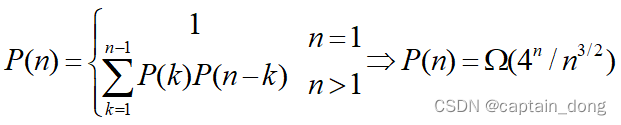
4.1.1 分析最优解的结构
- 将矩阵连乘积AiAi+1…Aj 简记为A[i:j], 这里i≤j;
- 考察计算A[1:n]的最优计算次序。
- 设这个计算次序在矩阵Ak和Ak+1之间将矩阵链断开,1≤k<n,则其相应完全加括号方式为(A1A2…Ak)(Ak+1Ak+2…An)
- 计算量:A[1:k]的计算量加上A[k+1:n]的计算量,
- 再加上A[1:k]和A[k+1:n]相乘的计算量
- 特征:计算A[1:n]的最优次序所包含的计算矩阵子链 A[1:k]和A[k+1:n]的次序也是最优的。
- 矩阵连乘计算次序问题的最优解包含着其子问题的最优解。
- 这种性质称为最优子结构性质。
- 问题的最优子结构性质是该问题可用动态规划算法求解的显著特征。
4.1.2 建立递归关系


4.1.3 计算最优值
- 对于1≤i≤j≤n不同的有序对(i, j)对应于不同的子问题。因此,不同子问题的个数最多只有
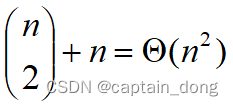
- 在递归计算时,许多子问题被重复计算多次。
- 这也是该问题可用动态规划算法求解的又一显著特征。
- 用动态规划算法解此问题,可依据其递归式以自底向上的方式进行计算。
- 在计算过程中,保存已解决的子问题答案。
- 每个子问题只计算一次,在后面需要时只要简单查一下,从而避免大量的重复计算,最终得到多项式时间的算法。

#define NUM 51
int p[NUM];
int m[NUM][NUM];
int s[NUM][NUM];
void MatrixChain (int n)
{for (int i=1; i<=n; i++) m[i][i] = 0;for (int r=2; r<=n; r++)for (int i=1; i<=n-r+1; i++) {int j=i+r-1; //计算初值,从i处断开m[i][j] = m[i+1][j]+p[i-1]*p[i]*p[j];s[i][j] = i; for (int k=i+1; k<j; k++) { int t = m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];if (t < m[i][j]) {m[i][j] = t; s[i][j] = k;}}}
}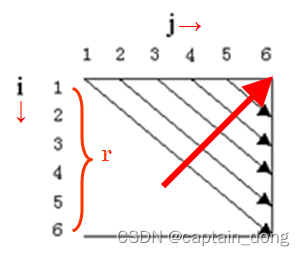
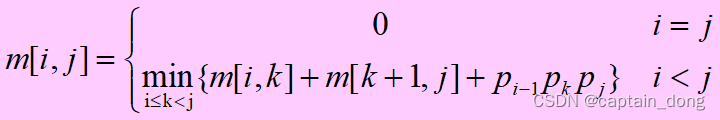
4.1.3 计算最优值
计算顺序
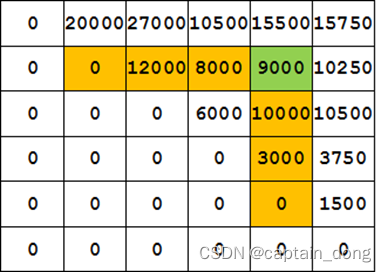

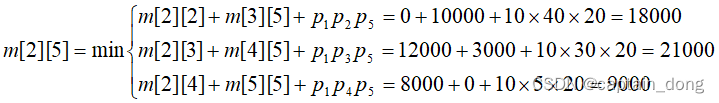
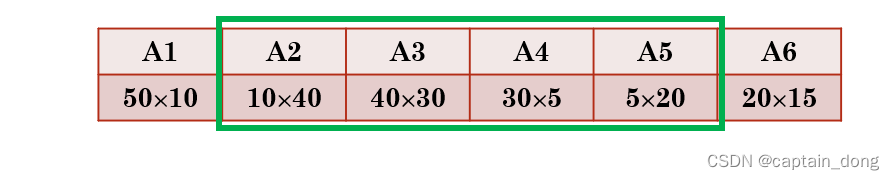
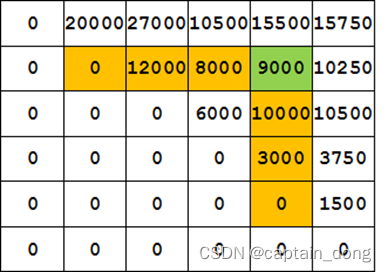
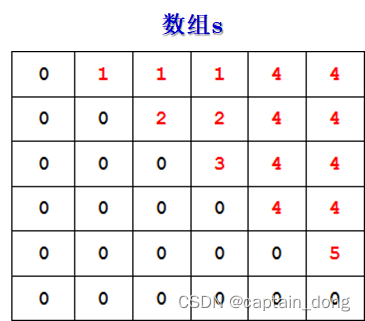
- 依据其递归式以自底向上的方式进行计算。
- 在计算过程中 , 保存已解决的子问题答案。
- 每个子问题只计算一次 , 而在后面需要时只要简单查一下 ,从而避免大量的重复计算, 最终得到多项式时间的算法。


计算顺序
4.1.3 构造最优解
- s[i][j]已经存储了构造最优解所需要的足够的信息。
- 每个部分的最优加括号方式可以根据数组s的相应元素得出。
- 照此递推下去,最终可以确定A[1:n]的最优完全加括号方式,即构造出问题的一个最优解。
//算法4.2计算矩阵连乘积最优解的递归算法
void TraceBack(int i, int j)
{ if(i==j) printf("A%d", i);else {printf("(");TraceBack(i,s[i][j]); TraceBack(s[i][j]+1,j); printf(")"); }
}

4.2 动态规划算法的基本要素
4.2.1 最优子结构
- 设计动态规划算法的第一步是刻画最优解的结构。
- 当问题的最优解包含其子问题的最优解时,称该问题具有最优子结构性质。
- 问题的最优解子结构性质提供了该问题可用动态规划求解的重要线索。
- 动态规划算法中,利用问题的最优子结构性质,以自底向上的方法递归的从子问题的最优解逐步构造出整个问题的最优解。
- 使我们能在相对小的子问题空间中考虑问题。
4.2.2 重叠子问题
- 递归算法求解问题时,每次产生的子问题并不总是新问题,有些子问题被反复计算多次。
- 这种性质称为子问题的重叠性质。
- 动态规划算法,对每一个子问题只解一次,而后将其解保存在一个表格中,当再次需要解此子问题时,只是简单地用常数时间查看一下结果。
- 通常不同的子问题个数随问题的大小呈多项式增长。
- 用动态规划算法只需要多项式时间,从而获得较高的解题效率。

算法4.3 计算矩阵连乘积的递归算法
//算法4.3 计算矩阵连乘积的递归算法int Recurve(int i, int j)
{if (i == j) return 0;int u = Recurve(i, i)+Recurve(i+1,j)+p[i-1]*p[i]*p[j];s[i][j] = i;for (int k = i+1; k<j; k++) {int t = Recurve(i, k) + Recurve(k+1,j)+p[i-1]*p[k]*p[j];if (t<u) { u = t; s[i][j] = k;}}m[i][j] = u;return u;
}
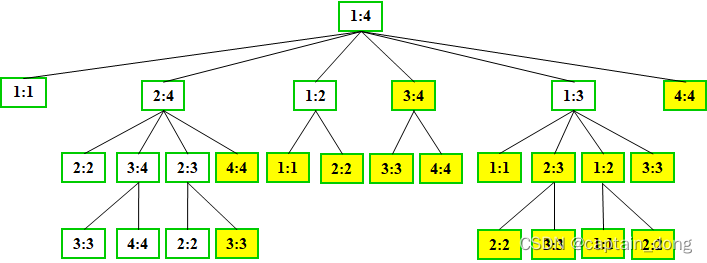
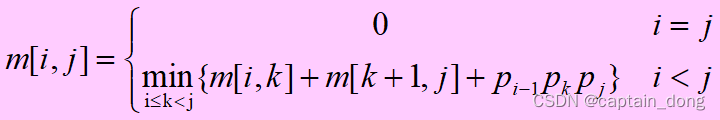
4.1.3 备忘录方法
- 备忘录方法是动态规划算法的变形。
- 与动态规划算法一样,备忘录方法用一个表格保存已解决的子问题的答案,再碰到该子问题时,只要简单地查看该子问题的解答,而不必重新求解。
- 备忘录方法的控制结构与直接递归方法的控制结构相同,区别仅在于备忘录方法为每个解过的子问题建立了备忘录以备需要时查看,避免了相同子问题的重复求解。
算法4.4计算矩阵连乘积的备忘录算法
int LookupChai (int i, int j)
{if (m[i][j]>0) return m[i][j];if (i==j) return 0;int u = LookupChain(i,i)+LookupChain(i+1,j)+p[i-1]*p[i]*p[j];s[i][j] = i;for (int k = i+1; k<j; k++) {int t = LookupChain(i,k)+LookupChain(k+1,j)+p[i-1]*p[k]*p[j];if (t < u) { u = t; s[i][j] = k;}}m[i][j] = u;return u;
}
4.3 最长公共子序列
- 若给定序列X={x1,x2,…,xm},则另一序列Z={z1,z2,…,zk},是X的子序列是指存在一个严格递增下标序列{i1,i2,…,ik}使得对于所有j=1,2,…,k有:zj=xij。
- 例如,序列Z={B,C,D,B}是序列X={A,B,C,B,D,A,B}的子序列,相应的递增下标序列为{2,3,5,7}。
- 给定2个序列X和Y,当另一序列Z既是X的子序列又是Y的子序列时,称Z是序列X和Y的公共子序列。
- 给定2个序列X={x1,x2,…,xm}和Y={y1,y2,…,yn},找出X和Y的最长公共子序列。
- 设序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}的最长公共子序列为Z={z1,z2,…,zk} ,则
- 若xm=yn,则zk=xm=yn,且zk-1是xm-1和yn-1的最长公共子序列。
- 若xm≠yn且zk≠xm,则Z是xm-1和Y的最长公共子序列。
- 若xm≠yn且zk≠yn,则Z是X和yn-1的最长公共子序列。

4.3.2 子问题的递归结构
- 由最长公共子序列问题的最优子结构性质可知,要找出X和Y的最长公共子序列,可按以下方式递归地进行:
- 当xm=yn时,找出Xm-1和Yn-1的最长公共子序列,然后在其尾部加上xm(=yn)即可得X和Y的一个最长公共子序列。
- 当xm≠yn时,必须解两个子问题,即找出Xm-1和Y的一个最长公共子序列及X和Yn-1的一个最长公共子序列。这两个公共子序列中较长者为X和Y的一个最长公共子序列。
- 用c[i][j]记录序列和的最长公共子序列的长度。
- Xi={x1,x2,…,xi};Yj={y1,y2,…,yj}。
- 当i=0或j=0时,空序列是Xi和Yj的最长公共子序列。
- 故此时C[i][j]=0。
- 其它情况下,由最优子结构性质可建立递归关系如下:
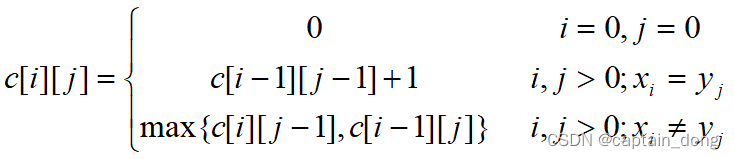
4.3.3 计算最优值
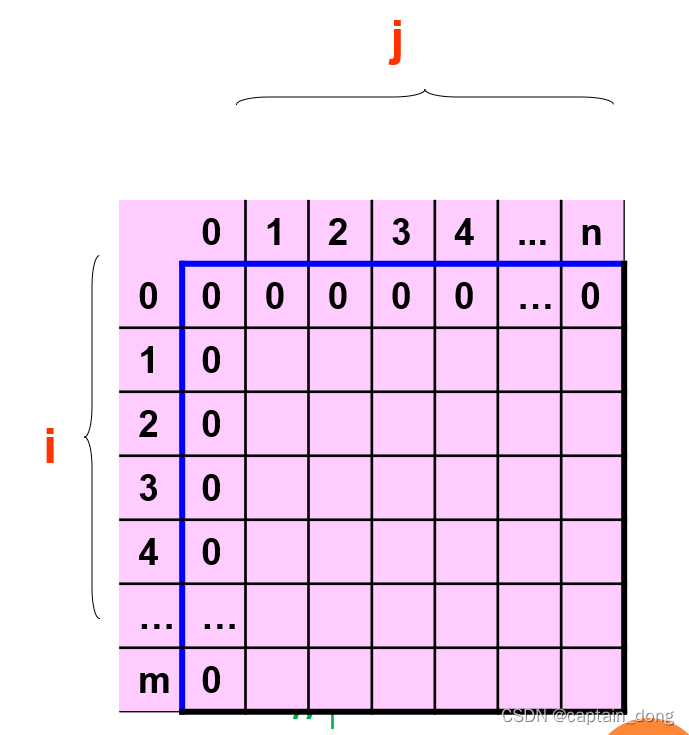
//算法4.5计算最长公共子序列的动态规划算法
#define NUM 100
int c[NUM][NUM];
int b[NUM][NUM];
void LCSLength (int m, int n, const char x[],char y[])
{ int i,j;//数组c的第0行、第0列置0for (i = 1; i <= m; i++) c[i][0] = 0;for (i = 1; i <= n; i++) c[0][i] = 0;//根据递推公式构造数组cfor (i = 1; i <= m; i++)for (j = 1; j <= n; j++){if (x[i]==y[j]) {c[i][j]=c[i-1][j-1]+1; b[i][j]=1; } //↖else if (c[i-1][j]>=c[i][j-1]) {c[i][j]=c[i-1][j]; b[i][j]=2; } //↑else { c[i][j]=c[i][j-1]; b[i][j]=3; } //←}
}




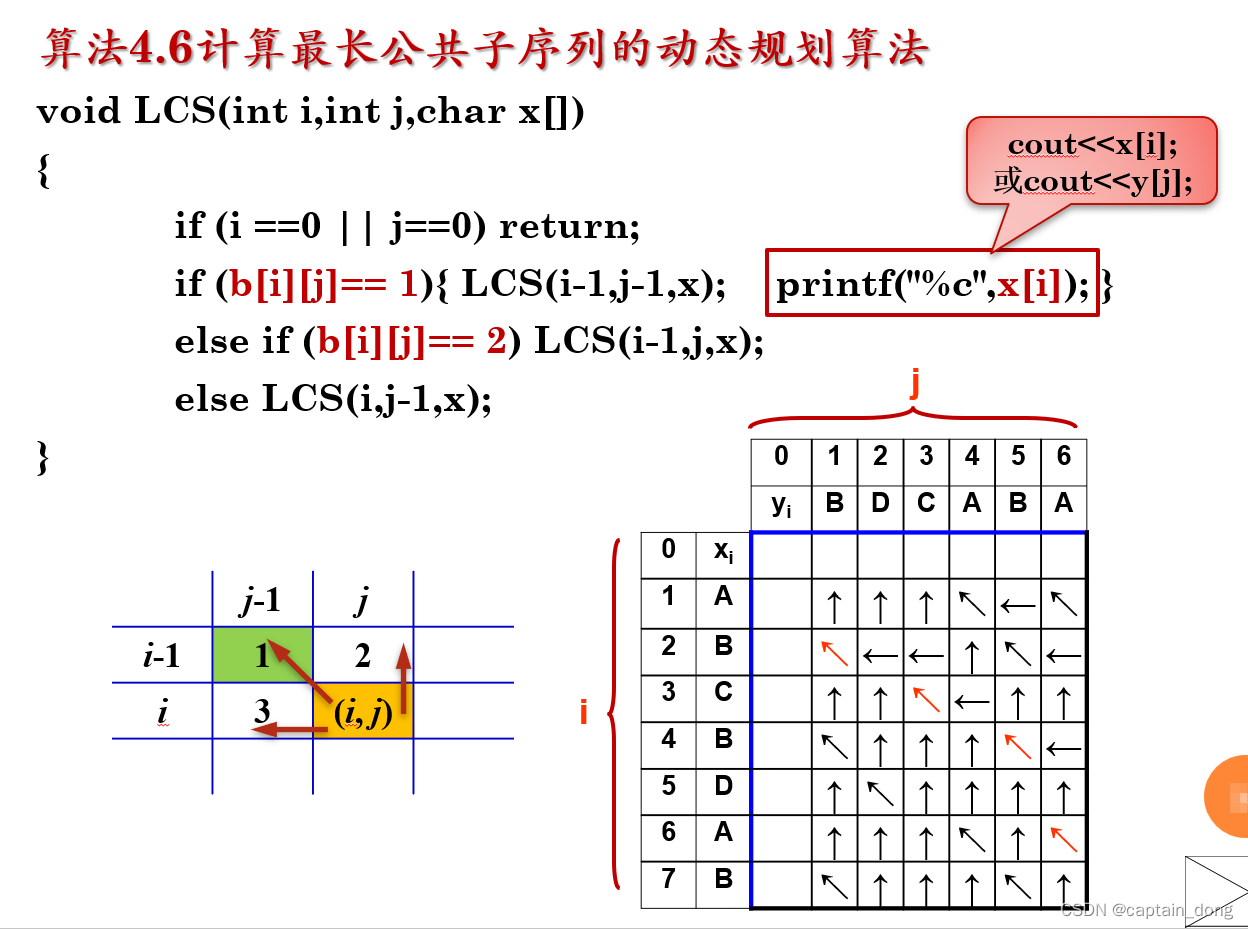
4.4 最大子段和
- 给定由n个整数(包含负整数)组成的序列a1,a2,...,an,求该序列子段和的最大值。
- 当所有整数均为负值时定义其最大子段和为0。
- 所求的最优值为:
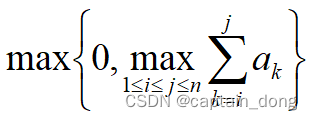
- 例如,当(a1,a2, ……a7,a8)=(1,-3, 7,8,-4,12, -10,6)时,最大子段和为:
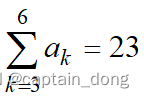
- bj是1到j位置的最大子段和:
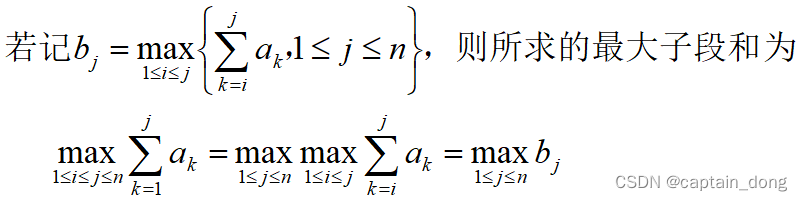

相关文章:

C++-----动态规划
目录 一、动态规划的基本思想 二、设计动态规划法的步骤 三、动态规划问题的特征 4.1 矩阵连乘积问题 4.1.1 分析最优解的结构 4.1.2 建立递归关系 4.1.3 计算最优值 4.1.3 计算最优值 4.1.3 构造最优解 4.2 动态规划算法的基本要素 4.2.1 最优子结构 4.2.2 重叠子问题 …...
2.2 Linux控制台访问CLI
系列文章目录 第1章 Linux Shell简介 第2章 Shell基础 <本章所在位置> 第3章 Bash Shell基础命令 第4章 Bash Shell命令进阶 第5章 Linux Shell深度理解 第6章 Linux环境变量 第7章 Linux文件权限 第8章 Linux文件系统的管理 第9章 Linux软件安装 第10章 Linux文本编辑器…...

代码随想录补打卡 509 斐波那契数列
代码如下 //斐波那契数列的第0项是0 第一项是1 func fib(n int) int { if n < 1 { return n } dp : make([]int,n1) dp[0] 0 dp[1] 1 for i : 2 ; i < n ; i { dp[i] dp[i-1] dp[i-2] } return dp[n] } 70 爬楼梯 代码如下 func climbStairs(n int) int …...

【每日一题Day195】LC1003检查替换后的词是否有效 | 栈
检查替换后的词是否有效【LC1003】 给你一个字符串 s ,请你判断它是否 有效 。 字符串 s 有效 需要满足:假设开始有一个空字符串 t "" ,你可以执行 任意次 下述操作将 t 转换为 s : 将字符串 "abc" 插入到 t…...
简单理解什么是序列化
为什么要序列化 序列化的目的就是为了对象可以在网络层进行传输, 比如通过后端传给前端数据。 什么是序列化 我们以Java为例。 序列化就是把对象转化为可传输的字节序列过程,这个字节序列可以是字符串,比如JSON格式的字符串,把…...
Django初识
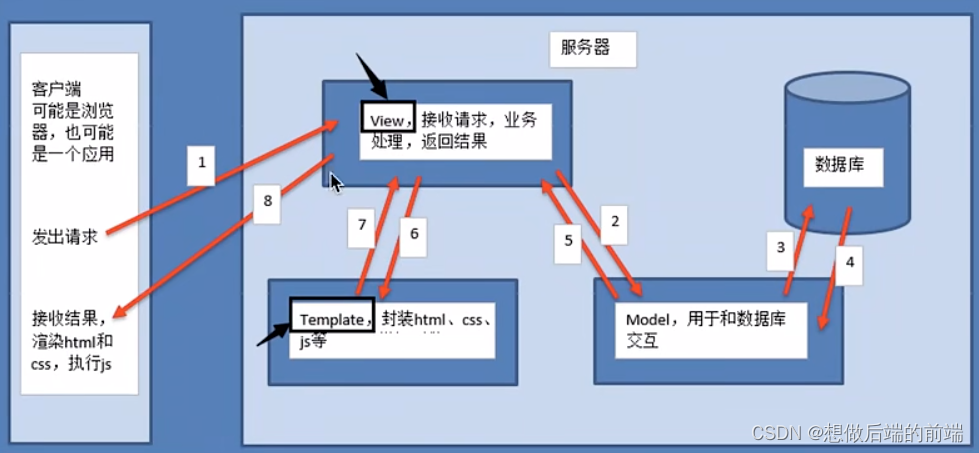
1、简介 Django,是用python语言写的开源web开发框架,并遵循MVC设计。劳伦斯出版集团为了开发以新闻内容为主的网站,而开发出来了这个框架,于2005年7月在BSD许可证下发布。这个名称来源于比利时的爵士音乐家DjangoReinhardt&#…...
ARM嵌入式编译器-volatile关键字对编译器优化的影响
volatile限定符告知计算机,其他agent(而不是变量所在的程序)可以改变该变量的值。通常它被用于硬件地址以及在其他程序或同时运行的线程中共享数据。要求编译器不要对其描述的对象作优化处理,对它的读写都需要从内存中访问。 使用…...

销售数据分析怎么做?这篇文章说清楚了
如何分析销售数据?分析销售数据有哪些指标?销售数据分析有什么作用? 销售数据是不是得通过数据分析软件啊? 本文将为您解答疑惑—— 一、分析销售数据的指标 从两个层面上来讲,一个是对销售情况的整体把控…...

二十六、ISIS技术总结
文章目录 ISIS 概述一、路由协议总结1、路由优先级2、分类 二、ISIS 协议特点1、特点2、ISIS 路由器的种类 三、ISIS 配置1、基础配置2、network-entity含义3、router id 和系统id转换规则 四、ISIS 开销计算1、Narrow 模式2、Wide 模式 五、 ISIS 和 OSPF 的区别 ISIS 概述 I…...

三菱m70 m80系统解密 三菱m80机床到期解锁
我们从操作系统的发展讲起,为什么要有线程这个概念出现。《Java多线程学习笔记(一) 初遇篇》讲Java平台下的线程,如何使用和创建,以及引入线程后所面临的问题,为了解决线程安全问题,Java引入的机制,这也是《…...
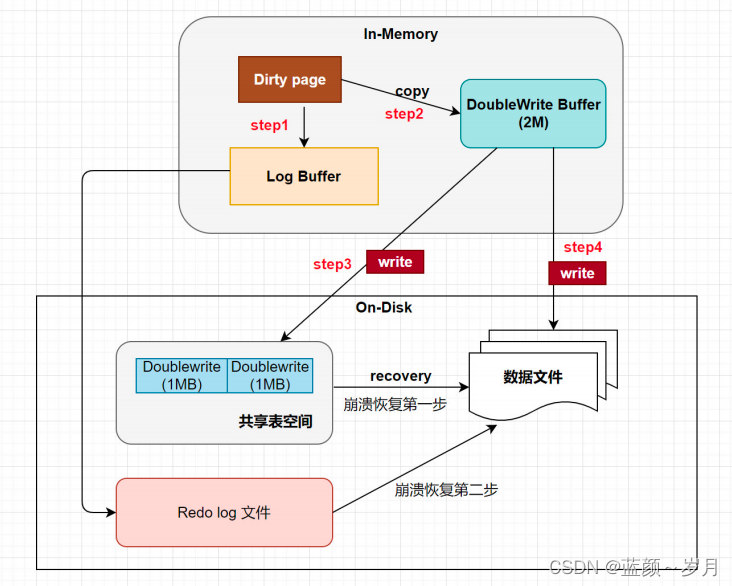
InnoDB 磁盘结构之数据字典和双写缓冲区
数据字典(InnoDB Data Dictionary) MySQL中,数据字典包括了: 表结构、数据库名或表名、字段的数据类型、视图、索引、表字段信息、MySQL版本信息、存储过程、触发器等内容 InnoDB数据字典由内部系统表组成,这些表包含用于查找表…...

Django模型层part two - 多表关系创建和多表操作
前言 继续上面一篇文章的内容,本文介绍多表操作。使用django ORM可以创建多表关系,并且也支持多张表之间的操作,以创建表关系和查询两部分说明django ORM的多表操作。以作者、图书、出版社和作者信息几张表作为案例进行说明。 创建表关系 …...

智能优化算法:浣熊优化算法-附代码
智能优化算法:浣熊优化算法 文章目录 智能优化算法:浣熊优化算法1.浣熊优化算法1.1 初始化1.2 阶段一:狩猎和攻击(探索阶段) 2.实验结果3.参考文献4. Matlab 摘要:浣熊优化算法(Coati Optimizat…...
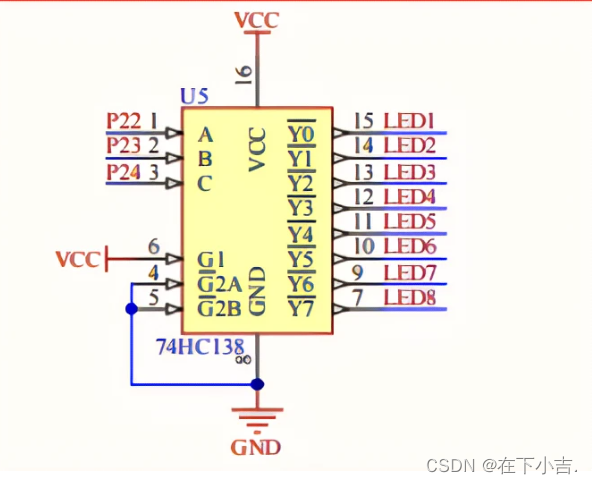
【51单片机】数码管显示(样例展示以及异常分析)
🎊专栏【51单片机】 🍔喜欢的诗句:更喜岷山千里雪 三军过后尽开颜。 🎆音乐分享【如愿】 大一同学小吉,欢迎并且感谢大家指出我的问题🥰 ⭐数码管 比如要显示“6”,那么下面图片中,AFEDCG=1,B=0 对应到数码管上,就是 ⭐原理 🎊P22~P24控制LED1~...

Android InputChannel事件发送接收系统分析
本文基于Android12。 InputChannel表示其他进程通过文件描述符传递输入事件到View的通道,因为需要跨进程传输,实现了Parcelable序列化接口,所以也能够理解Java层的InputChannel后面为什么使用copyTo()方法初始化。 输入事件的接收方是View&…...
-- LocalDate()类)
Java时间类(五)-- LocalDate()类
目录 引言: 1. LocalDate的概述: 2. LocalDate的常用方法: 引言: (1)Date存在的缺陷: 如果不格式化,打印出的日期可读性差://获取当前时间Date date = new Date();System.out.println("date = " + date); //date = Wed May 03 22:30:24 CST...
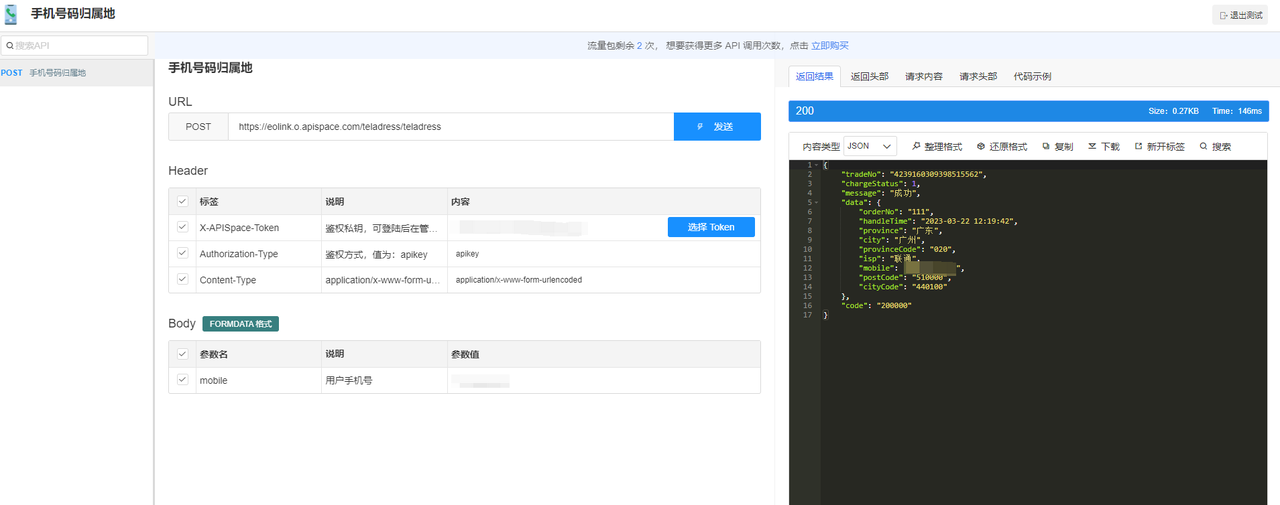
用手机号码归属地 API 开发的应用推荐
引言 手机号码归属地 API是一种提供手机号码归属地信息的接口,通过该接口,可以获取手机号码所属的省份、城市、运营商等信息。它可以帮助企业更好地了解客户,为个性化推荐和精准广告投放提供数据支持。作为一种数据服务,手机号码…...
测试从业第 3 年,我看到了终点......
先说明,今天的内容,是写给想成为高级测试开发、自动化测试专家的人看的,因为,它可能颠覆你的认知。 众所周知,如今无论是大厂还是中小厂,自动化测试基本是标配了,毕竟像双11、618 这种活动中庞…...

结巴分词原理分析
结巴分词器工作原理 结巴分词是一款python写成的开源中文分词器,分词过程大致如下: 首先,结巴使用正则表达式将输入文本切割成若干中文块,接着对每个中文块B做处理,将B转成有向无环图(DAG)。DAG是以{key:list[i,j...…...

JavaEE 第三-四周
计算机Z20-第3-4周作业 总分:100分 得分:74.2分 1 . 填空题 简单 5分 在web.xml文件中,<url-pattern>/xxxxServlet</url-pattern>中的第一个‘/’表示__________。 学生答案 当前web应用程序的根目录 2 . 填空题 简…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

