( 数组和矩阵) 565. 数组嵌套 ——【Leetcode每日一题】
❓565. 数组嵌套
难度:中等
索引从 0 开始长度为N的数组 A,包含 0 到 N - 1 的所有整数。找到最大的集合 S并返回其大小,其中 S[i] = {A[i], A[A[i]], A[A[A[i]]], ... } 且遵守以下的规则。
假设选择索引为 i 的元素 A[i] 为 S 的第一个元素,S 的下一个元素应该是 A[A[i]],之后是 A[A[A[i]]]... 以此类推,不断添加直到 S 出现重复的元素。
示例 1:
输入: A = [5,4,0,3,1,6,2]
输出: 4
解释:
A[0] = 5, A[1] = 4, A[2] = 0, A[3] = 3, A[4] = 1, A[5] = 6, A[6] = 2.
其中一种最长的 S[K]:
S[0] = {A[0], A[5], A[6], A[2]} = {5, 6, 2, 0}
提示:
- 1 < = n u m s . l e n g t h < = 1 0 5 1 <= nums.length <= 10^5 1<=nums.length<=105
- 0 <= nums[i] < nums.length
A中不含有重复的元素。
💡思路:图
我们可以从 i 向 nums[i] 连边,我们可以得到一张有向图。由于所有数范围都在 [0, N−1],且不重复,因此至少存在一个环,而问题本质是求所有环的最大长度。
遍历数组nums,遍历过程中防止某些环被重复处理,对于当前经过的 nums[i] 标记为 -1,这样每个数被访问的次数最多不超过 3 次,整体复杂度为 O ( n ) O(n) O(n)。
🍁代码:(Java、C++)
Java
class Solution {public int arrayNesting(int[] nums) {int ans = 0;for(int i = 0; i < nums.length; i++){int cnt = 0;for(int j = i; nums[j] != -1; ){int tmp = nums[j];nums[j] = -1;j = tmp;cnt++;}ans = Math.max(ans, cnt);}return ans;}
}
C++
class Solution {
public:int arrayNesting(vector<int>& nums) {int ans = 0;for(int i = 0; i < nums.size(); i++){int cnt = 0;for(int j = i; nums[j] != -1; ){int tmp = nums[j];nums[j] = -1;j = tmp;cnt++;}ans = max(ans, cnt);}return ans;}
};
🚀 运行结果:
🕔 复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n),其中
n为数组的长度。 - 空间复杂度: O ( 1 ) O(1) O(1),我们只需要常数的空间保存若干变量。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我 leetCode专栏,每日更新!
注: 如有不足,欢迎指正!
相关文章:

( 数组和矩阵) 565. 数组嵌套 ——【Leetcode每日一题】
❓565. 数组嵌套 难度:中等 索引从 0 开始长度为N的数组 A,包含 0 到 N - 1 的所有整数。找到最大的集合 S并返回其大小,其中 S[i] {A[i], A[A[i]], A[A[A[i]]], ... } 且遵守以下的规则。 假设选择索引为 i 的元素 A[i] 为 S 的第一个元…...

linux内核网络子系统初探---概述
linux内核网络子系统初探—概述 一、网络模型 简单介绍 学习网络时,必定能在各种教材资料里见到以下三种网络模型: 三种模型间的差异: OSI七层模型是理论上的网络模型,从功能方面分成了相对独立的7个层次,由于太复…...

java版工程项目管理系统源代码-功能清单 图文解析
Java版工程项目管理系统 Spring CloudSpring BootMybatisVueElementUI前后端分离 功能清单如下: 首页 工作台:待办工作、消息通知、预警信息,点击可进入相应的列表 项目进度图表:选择(总体或单个)项目显示…...

【chapter30】【PyTorch】[动量与学习率衰减】
前言: SGD的不足: ①呈“之”字型,迂回前进,损失函数值在一些维度的改变得快(更新速度快),在一些维度改变得慢(速度慢)- 在高维空间更加普遍 ②容易陷入局部极小值和鞍点…...
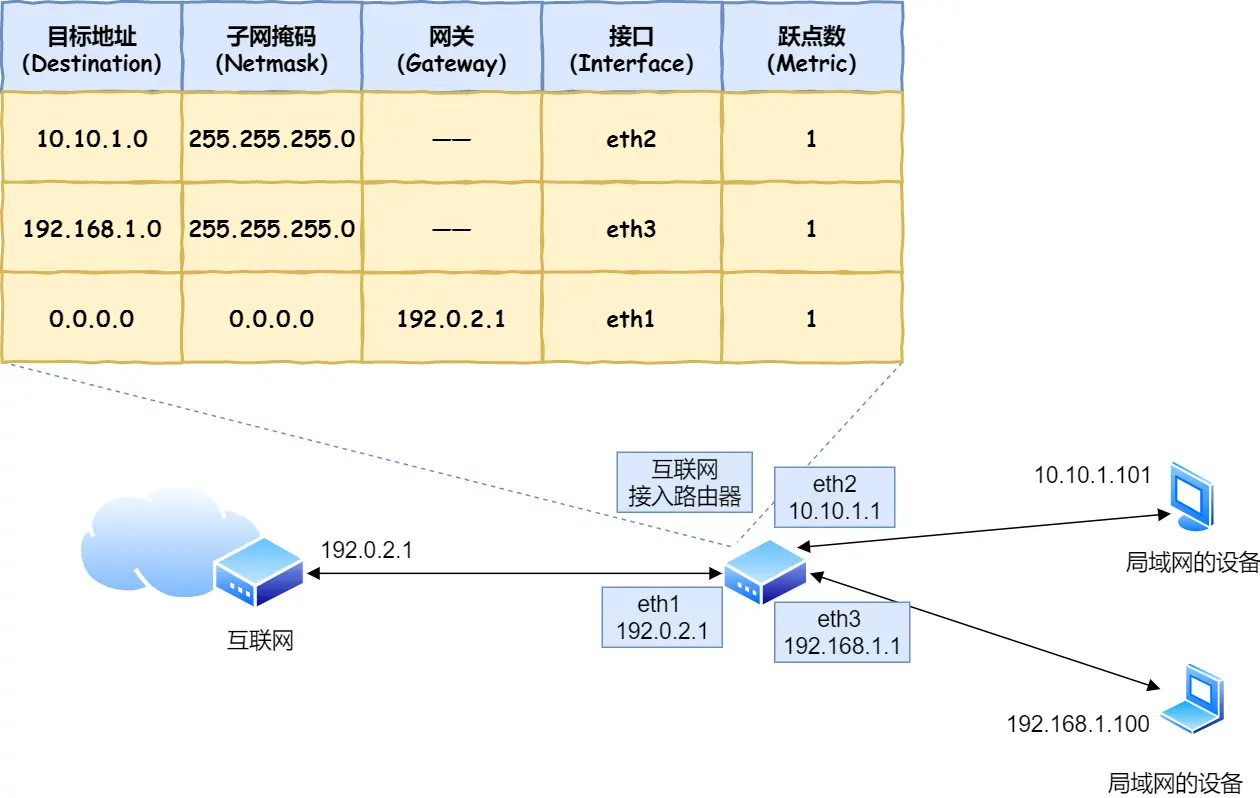
【键入网址到网页显示】
文章目录 HTTPDNS五层协议TCPIPMAC网卡(物理层)交换机路由器 HTTP 对 URL 进行解析之后,浏览器确定了 Web 服务器和文件名,接下来就是根据这些信息来生成 HTTP 请求消息了。 http://www.server.com/dir1/file1.html http:访问数…...

Nacos配置中心、配置热更新、及配置共享的记录
Nacos除了提供了注册中心的功能,同样也提供了配置中心的功能,用于管理一些叫常改动的配置 当微服务部署的实例越来越多,达到数十、数百时,逐个修改微服务配置就会让人抓狂,而且很容易出错。我们需要一种统一配置管理方案,可以集中…...
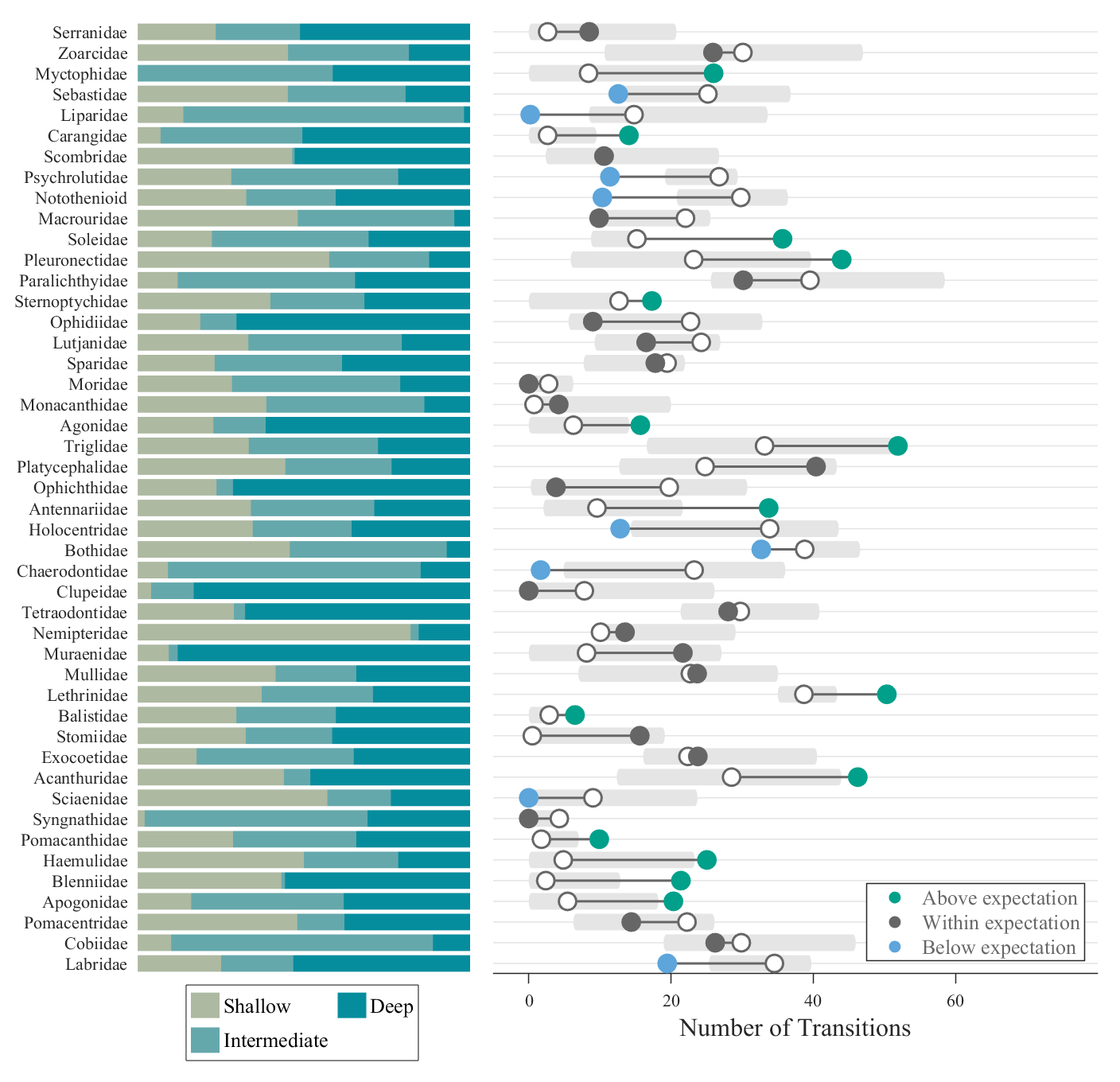
MATLAB | 绘图复刻(八) | 堆叠柱状图+哑铃图
本次复刻的是Nature Communications中Friedman, S.T., Muoz, M.M. A latitudinal gradient of deep-sea invasions for marine fishes. Nat Commun 14, 773 (2023). https://doi.org/10.1038/s41467-023-36501-4的Fig1图像: 复刻效果: 文章可在如下网站下…...

Scala之集合(2)
目录 集合基本函数: (1)获取集合长度 (2)获取集合大小 (3)循环遍历 (4)迭代器 (5)生成字符串 (6)是否包含 衍生集合…...

【图像分割】视觉大模型SEEM(Segment Everything Everywhere All at Once)原理解读
文章目录 摘要(效果)二、前言三、相关工作四、method4.1 多用途4.2 组合性4.3 交互式。4.4 语义感知 五、实验 论文地址:https://arxiv.org/abs/2304.06718 测试代码:https://github.com/UX-Decoder/Segment-Everything-Everywher…...

Linux: command: ibstat; infiniband
文章目录 如何在Linux上安装infiniband相关的软件。ibstat相关资料 如何在Linux上安装infiniband相关的软件。 https://access.redhat.com/solutions/301643 https://docs.oracle.com/cd/E19436-01/820-3522-10/ch3-linux.html yum groupinstall “Infiniband Support” Pack…...
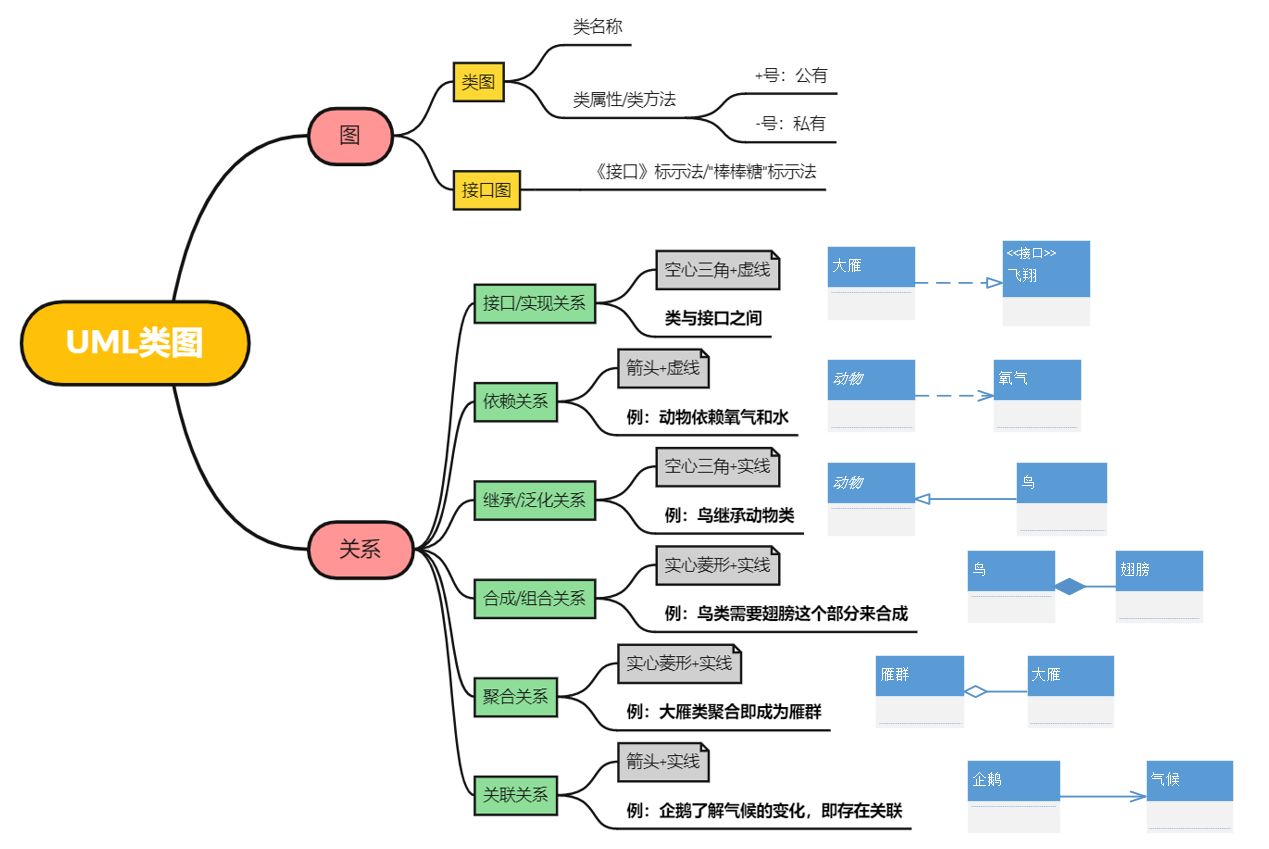
UML简介与类图详解
1 UML简介 1.1 UML是什么 UML,全称为Unified Model Language,即统一建模语言,是由一整套图表组成的,为面向对象系统的产品进行说明、可视化和编制文档的一种标准语言。UML 代表了一组最佳工程实践,这些实践已被证明在…...

【每日一题】1994.好子集的数目
1994.好子集的数目 题目描述解决方案:状态压缩动态规划代码:Python 题目来源:LeetCode 原文链接:https://mp.weixin.qq.com/s/myI7_ZwJM7kizrwUtWgAZQ 难度级别:困难 题目描述 给你一个整数数组 nums。如果 nums 的一…...

坚持伙伴优先,共创数据存储新生态
4 月 26 日,2023 阿里云合作伙伴大会上,阿里巴巴集团董事会主席兼 CEO、阿里云智能集团 CEO 张勇表示,阿里云的核心定位是一家云计算产品公司,生态是阿里云的根基。让被集成说到做到的核心,是要坚定走向“产品被集成”…...
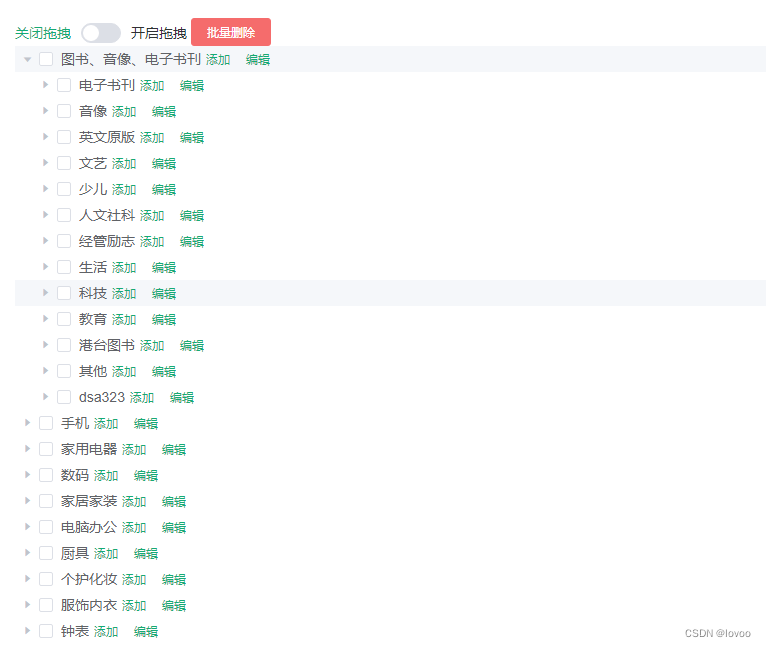
树形结构的三级分类如何实现?
概述: 本三级联动分类服务端使用的是: Springboot MyBatis-plus,前端使用的是:VueElementUI,树形控件使用的是el-tree。本三级联动分类可以把任一子项拖拽到其它目录,可以添加、编辑、删除分类。 效果图:…...

SSM整合完整流程
🏠个人主页:shark-Gao 🧑个人简介:大家好,我是shark-Gao,一个想要与大家共同进步的男人😉😉 🎉目前状况:23届毕业生,目前在某公司实习…...

虹科方案 | 助力高性能视频存储解决方案-2
上篇文章《虹科方案 | 助力高性能视频存储解决方案-1》我们分享了虹科&ATTO 和 Avid 共同创建协作解决方案,助力高性能视频存储,今天我们再深入介绍一下我们的案例详情。 一、行业挑战 从高端广播设施到小型独立工作室的媒体后期制作环境都需要允许多…...

java版深圳 工程管理系统软件 自主研发,工程行业适用 软件源码
Java版工程项目管理系统 Spring CloudSpring BootMybatisVueElementUI前后端分离 功能清单如下: 首页 工作台:待办工作、消息通知、预警信息,点击可进入相应的列表 项目进度图表:选择(总体或单个)项目显示…...
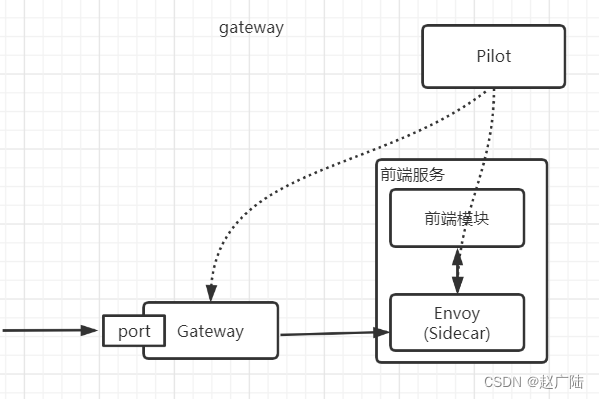
云原生Istio架构和组件介绍
目录 1 Istio 架构2 Istio组件介绍2.1 Pilot2.2 Mixer2.3 Citadel2.4 Galley2.5 Sidecar-injector2.6 Proxy(Envoy)2.7 Ingressgateway2.8 其他组件 1 Istio 架构 Istio的架构,分为控制平面和数据面平两部分。 - 数据平面:由一组智能代理([En…...
吹爆,全网第一个手把手教你从零开始搭建Spring Cloud Alibaba的笔记
Spring Cloud Alibaba 是阿里巴巴提供的微服务开发一站式解决方案,是阿里巴巴开源中间件与 Spring Cloud 体系的融合。 Springcloud 和 Srpingcloud Alibaba 区别? SpringCloud: 部分组件停止维护和更新,给开发带来不便;SpringCl…...

企业短信遭疯狂盗用,可能是没配置验证码
手机短信作为一种快捷的通讯方式被广泛应用。不仅在个人日常生活中,企业也习惯使用手机短信来进行验证和提醒,以保证业务的正常进行。随着数字化的发展,手机短信也成为了不法分子滥用的目标之一,给个人和企业带来不同经济损失。 个…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
