BM61-矩阵最长递增路径
题目
给定一个 n 行 m 列矩阵 matrix ,矩阵内所有数均为非负整数。 你需要在矩阵中找到一条最长路径,使这条路径上的元素是递增的。并输出这条最长路径的长度。
这个路径必须满足以下条件:
- 对于每个单元格,你可以往上,下,左,右四个方向移动。 你不能在对角线方向上移动或移动到边界外。
- 你不能走重复的单元格。即每个格子最多只能走一次。
数据范围:1≤n,m≤1000,0≤matrix[i][j]≤1000。
进阶:空间复杂度 O(nm),时间复杂度 O(nm)。
例如:当输入为[[1,2,3],[4,5,6],[7,8,9]]时,对应的输出为5,其中的一条最长递增路径如下图所示:

示例1
输入:[[1,2,3],[4,5,6],[7,8,9]]
返回值:5
说明:1->2->3->6->9即可。当然这种递增路径不是唯一的。
示例2
输入:[[1,2],[4,3]]
返回值:4
说明: 1->2->3->4
备注:矩阵的长和宽均不大于1000,矩阵内每个数不大于1000。
思路1:深度优先搜索(dfs)(推荐使用)
深度优先搜索一般用于树或者图的遍历,其他有分支的(如二维矩阵)也适用。
它的原理是从初始点开始,一直沿着同一个分支遍历,直到该分支结束,然后回溯到上一级继续沿着一个分支走到底,如此往复,直到所有的节点都有被访问到。
既然是查找最长的递增路径长度,那我们首先要找到这个路径的起点,起点不好直接找到,就从上到下从左到右遍历矩阵的每个元素。然后以每个元素都可以作为起点查找它能到达的最长递增路径。
如何查找以某个点为起点的最长递增路径呢?我们可以考虑深度优先搜索,因为我们查找递增路径的时候,每次选中路径一个点,然后找到与该点相邻的递增位置,相当于进入这个相邻的点,继续查找递增路径,这就是递归的子问题。因此递归过程如下:
- 终止条件: 进入路径最后一个点后,四个方向要么是矩阵边界,要么没有递增的位置,路径不能再增长,返回上一级。
- 返回值: 每次返回的就是本级之后的子问题中查找到的路径长度加上本级的长度。
- 本级任务: 每次进入一级子问题,先初始化后续路径长度为0,然后遍历四个方向(可以用数组表示,下标对数组元素的加减表示去往四个方向),进入符合不是边界且在递增的邻近位置作为子问题,查找子问题中的递增路径长度。因为有四个方向,所以最多有四种递增路径情况,因此要维护当级子问题的最大值。
具体做法:
- step 1:使用一个dp数组记录i,j处的单元格拥有的最长递增路径,这样在递归过程中如果访问到就不需要重复访问。
- step 2:遍历矩阵每个位置,都可以作为起点,并维护一个最大的路径长度的值。
- step 3:对于每个起点,使用dfs查找最长的递增路径:只要下一个位置比当前的位置数字大,就可以深入,同时累加路径长度。
代码1
import java.util.*;public class Solution {//记录4个方向private int[][] dirs = new int[][] {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};private int n, m;public int solve (int[][] matrix) {//边界条件判断if (matrix.length == 0 || matrix[0].length == 0) {return 0;}int res = 0;n = matrix.length;m = matrix[0].length;//j,j处的单元格拥有的最长递增路径int[][] dp = new int[m + 1][n + 1];for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {//更新最大值res = Math.max(res, dfs(matrix, dp, i, j));}}return res;}//深度优先搜索,返回最大单元格数public int dfs(int[][] matrix, int[][] dp, int i, int j) {if (dp[i][j] != 0) {return dp[i][j];}dp[i][j]++;for(int k = 0; k < 4; k++) {int nexti = i + dirs[k][0];int nextj = j + dirs[k][1];//判断下一个要遍历的位置是否满足条件:在矩阵范围内且满足路径递增if(nexti >= 0 && nexti < n && nextj >= 0 && nextj < m && matrix[nexti][nextj] > matrix[i][j]) {dp[i][j] = Math.max(dp[i][j], dfs(matrix, dp, nexti, nextj) + 1);}}return dp[i][j];}
}- 时间复杂度:O(mn),m、n分别为矩阵的两边,遍历整个矩阵以每个点作为起点,然后递归相当于遍历填充dp矩阵。
- 空间复杂度:O(mn),辅助矩阵的空间是一个二维数组。
思路2:广度优先搜索(bfs)
广度优先搜索与深度优先搜索不同,它是将与某个节点直接相连的其它所有节点依次访问一次之后,再往更深处,进入与其他节点直接相连的节点。
bfs的时候我们常常会借助队列的先进先出,因为从某个节点出发,我们将与它直接相连的节点都加入队列,它们优先进入,则会优先弹出,在它们弹出的时候再将与它们直接相连的节点加入,由此就可以依次按层访问。
我们可以将矩阵看成是一个有向图,一个元素到另一个元素递增,代表有向图的箭头。这样我们可以根据有向图的出度入度找到最长的路径,且这个路径在矩阵中就是递增的。
具体做法:
- step 1:计算每个节点(单元格)所对应的出度(符合边界条件且递增),对于作为边界条件的单元格,它的值比所有的相邻单元格的值都要大,因此作为边界条件的单元格的出度都为0。利用一个二维矩阵记录每个单元格的出度
- step 2:利用拓扑排序的思想,从所有出度为0的单元格开始进行广度优先搜索。
- step 3:借助队列来广度优先搜索,队列中每次加入出度为0的点,即路径最远点,每次从A点到B点,便将A点出度减一。
- step 4:每次搜索都会遍历当前层的所有单元格,更新其余单元格的出度,并将出度变为0的单元格加入下一层搜索。
- step 5:当搜索结束时,搜索的总层数即为矩阵中的最长递增路径的长度,因为bfs的层数就是路径增长的层数。
代码
import java.util.*;public class Solution {//记录4个方向private int[][] dirs = new int[][] {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};private int n, m;public int solve (int[][] matrix) {//边界条件判断if (matrix.length == 0 || matrix[0].length == 0) {return 0;}int res = 0;n = matrix.length;m = matrix[0].length;//j,j处的单元格拥有的最长递增路径int[][] outdegrees = new int[m + 1][n + 1];for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {for (int k = 0; k < 4; k++) {int nexti = i + dirs[k][0];int nextj = j + dirs[k][1];if (nexti >= 0 && nexti < n && nextj >= 0 && nextj < m &&matrix[nexti][nextj] > matrix[i][j]) {//符合条件,记录出度outdegrees[i][j]++;}}}}//辅助队列Queue<Integer> q1 = new LinkedList<Integer>();Queue<Integer> q2 = new LinkedList<Integer>();for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (outdegrees[i][j] == 0) {//找到出度为0的入队q1.offer(i);q2.offer(j);}}}while (!q1.isEmpty()) {res++;int size = q1.size();for (int x = 0; x < size; x++) {int i = q1.poll();int j = q2.poll();//四个方向for (int k = 0; k < 4; k++) {int nexti = i + dirs[k][0];int nextj = j + dirs[k][1];//逆向搜索,所以下一步是小于if (nexti >= 0 && nexti < n && nextj >= 0 && nextj < m &&matrix[nexti][nextj] < matrix[i][j]) {//符合条件,出度递减outdegrees[nexti][nextj]--;if (outdegrees[nexti][nextj] == 0) {q1.offer(nexti);q2.offer(nextj);}}}}}return res;}
}- 时间复杂度:O(mn),m、n分别为矩阵的两边,相当于遍历整个矩阵两次。
- 空间复杂度:O(mn),辅助矩阵的空间是一个二维数组。
相关文章:

BM61-矩阵最长递增路径
题目 给定一个 n 行 m 列矩阵 matrix ,矩阵内所有数均为非负整数。 你需要在矩阵中找到一条最长路径,使这条路径上的元素是递增的。并输出这条最长路径的长度。 这个路径必须满足以下条件: 对于每个单元格,你可以往上ÿ…...
selenium——unittest框架
目录 一、unittest框架基本介绍二、unittest框架解析三、unittest框架使用方法1.测试固件2.测试套件3.用例的执行顺序4.忽略测试用例中的方法5.unittest断言6.HTML报告生成 一、unittest框架基本介绍 在进行selenium IDE脚本录制导出的脚本中,我们发现其中多了很多…...

matlab频谱分析详解
频谱分析是一种用于分析信号频率特征的方法,常用于信号处理、音乐分析、谐波产生等领域。MATLAB是一种功能强大的数字信号处理软件,提供了许多用于频谱分析的函数和工具箱。 本文将介绍如何使用MATLAB进行频谱分析,包括信号预处理、选择合适…...

用layui写用户登录页面遇到的问题
用layui写用户登录页面遇到的问题 1.在layui-row下面的layui-col-md还是换行 原因:link标签和script标签中的type属性没写,导致应该是script或者这个css没有识别出来 解决办法:link标签里面加上type为text/css, script标签中加上type为 2…...
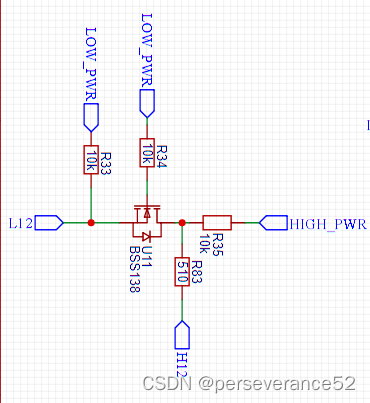
NMOS双向转换电路实测以及上升沿尖峰处理
NMOS双向转换电路实测以及上升沿尖峰处理 NMOS双向转换电路 🔧采用的是5V供电的STC8H单片机输出PWM波形,经过上面的电平转换电路测量低压端的波形。 ✨在做3.3V <>5V 电平转换电路方案验证时,输入5V PWM波形和输出波形的波形上升沿有尖…...
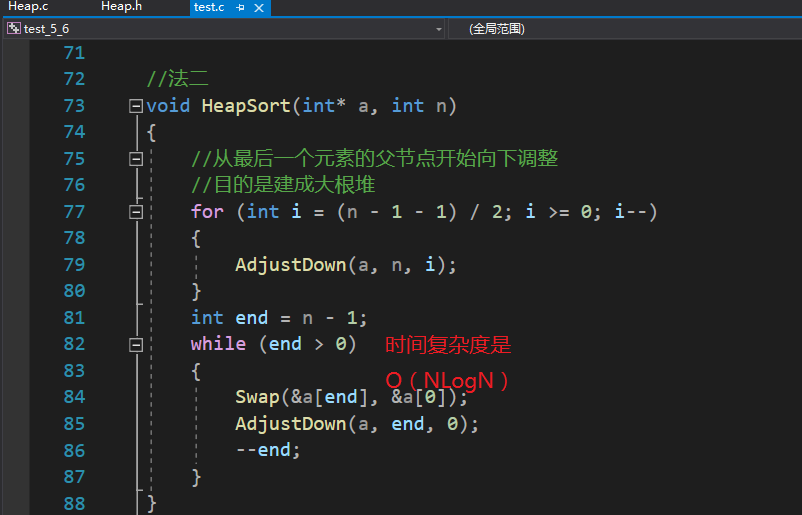
【数据结构】选择排序(详细)
选择排序 1. 直接选择排序2. 堆排序2.1 堆2.2 堆的实现(以大根堆为例)2.3 堆排序 3. 堆排序(topK问题) 1. 直接选择排序 思想 以排升序为例。以a[i]为最大值(或最小值),从a[i1]到a[n-1-i]比较选…...

什么是企业内容管理?
为什么出现企业内容管理? 在数字经济的宏观背景下,企业建立了各种应用系统以满足企业各业务的管理需求,这些系统每天都在产生大量的数据和信息资源,但在企业实践中存在很多数据或资源无法被应用系统获取、处理和共享。 比如发票…...

机器学习:分类、回归、决策树
分类:具有明确的类别 如:去银行借钱,会有借或者不借的两种类别 回归:不具有明确的类别和数值 如:去银行借钱,预测银行会借给我多少钱,如:1~100000之间的一个数值 不纯度࿱…...

java常见的异常,下一篇写如何正确处理异常
当我们编写Java程序时,经常会遇到各种异常情况。异常是指在程序执行过程中发生的一些错误或意外情况,它会打断程序的正常执行流程,并且需要被适当地处理。在Java中,异常被分为两种类型:可检查异常(Checked …...

C#开发的OpenRA游戏之网络协议打包和解包
C#开发的OpenRA游戏之网络协议打包和解包 OpenRA游戏里,由于这是一个网络游戏,那么与服务器通讯就缺少不了, 既然要通讯,那么就需要协议,有协议就需要对数据进行打包和解包, 这个过程其实就是序列化与反序列化的过程。 游戏里很多命令都需要发送给服务器,以便服务器同…...

K8S通过Ansible安装集群
K8S通过Ansible安装集群 K8S集群安装可参考https://gitee.com/open-hand/kubeadm-ha.git、https://github.com/easzlab/kubeasz.git 安装高可用集群 git clone https://gitee.com/open-hand/kubeadm-ha.git && cd kubeadm-ha升级内核,非必需,默认不升级&…...

ChatGPT辩证观点:“人才不是一个企业的核心竞争力,对人才的管理能力才是一个企业的核心竞争力”
一、问: “人才不是一个企业的核心竞争力,对人才的管理能力才是一个企业的核心竞争力”这句话的理解和误解,这句话有哪个中心论点转移和变化 二、ChatGPT答: 这句话的理解和误解: 理解:这句话的意思是说…...

windows11 永久关闭windows defender的方法
1、按键盘上的windows按键,再点【设置】选项。 2、点击左侧菜单的【隐私和安全性】,再点击列表的【Windows安全中心】选项。 3、点击界面的【病毒和威胁保护】设置项。 4、病毒保护的全部关闭 5、别人的图(正常是都开着的) 6、终极…...

继承的基本知识
概念 假设基于A类,创建了B类,那么称A为B的父类,B为A的子类 子类会继承父类的成员变量及成员函数,但是不能继承构造、析构、运算符重载 假设又基于B创建了C,那么称B为C的直接基类,A为C的间接基类 继承按…...
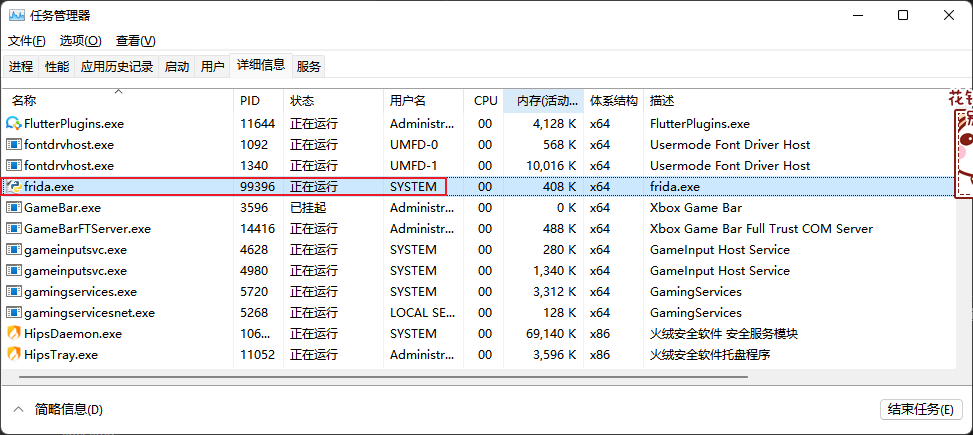
【Frida-实战】EA游戏平台的文件监控(PsExec.exe提权)
▒ 目录 ▒ 🛫 问题描述环境 1️⃣ 代码编写开源代码搜索自己撸代码procexp确定句柄对应的文件名并过滤 2️⃣ PsExec.exe提权定位找不到EABackgroundService.exe的问题 PsExec.exe提权PsExec.exe原理 🛬 结论📖 参考资料 🛫 问题…...

可视化和回归分析星巴克咖啡在中国的定价建议
可视化和回归分析星巴克咖啡在中国的定价建议。星巴克的拿铁大杯Tall 在各国的价格。 Claude AI | 代码自动生成的数据可视化代码 选择Claude AI 而非 ChatGPT的理由是前者更懂中文!具体可以参见我前面的两篇文章对比两者的中英文翻译的表现及使用安装等难易程度…...

热门影片怎么买票比较便宜,低价买电影票的方法,纯攻略!
有时候真的有被自己蠢到!看电影看了这么多年,竟然不知道电影票价格才9.9元、19.9元就能买到。之前我看电影动不动就是几十上百块,感觉好亏啊。 其实,我也不敢相信的,通过这些平台,同时在节假日甚至春节档期…...

Python通过SWIG调用C++时出现的ImportError问题解析
摘要 win10系统,编译器为mingw,按照教程封装C的一个类并用python调用,一步步进行直到最后一步运行python代码时,在python代码中import example时报错ImportError: DLL load failed while importing _example: The specified modul…...

3ds Max云渲染有多快,3ds Max云渲染怎么用?
本地渲染效果图和动画3D项目是一个非常耗时的过程,当在场景中使用未优化的几何体或在最终渲染中使用大量多边形模型时,诸如此类的变量最终会增加渲染项目所需的时间和处理器能力。随着提供的渲染服务的云渲染平台出现,越来越多动画师、艺术家…...

Java之线程安全
目录 一.上节回顾 1.Thread类常见的属性 2.Thread类中的方法 二.多线程带来的风险 1.观察线程不安全的现象 三.造成线程不安全现象的原因 1.多个线程修改了同一个共享变量 2.线程是抢占式执行的 3.原子性 4.内存可见性 5.有序性 四.解决线程不安全问题 ---synchroni…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...
