ACM - 其他算法 - 基础(前缀和 + 差分)
ACM- 其他算法
- 一、前缀和
- 模板
- 例题1、区间余数求K倍区间个数:AcWing 1230. K倍区间
- 例题2、前缀和+哈希求最长个数平分子串:Leetcode 面试题 17.05 字母与数字
- 二、差分
- 1、一维差分
- 2、二维差分
一、前缀和
模板
//一维前缀和
S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]//二维前缀和
S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
例题1、区间余数求K倍区间个数:AcWing 1230. K倍区间
原题链接: https://www.acwing.com/problem/content/1232/
(原题来源: 第八届蓝桥杯省赛C++B组,第八届蓝桥杯省赛JAVAB组)

import java.util.Scanner;public class Main{public static int[] sum = new int[100010]; //前缀和取模后public static int[] cnt = new int[100010]; //个数public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();int k = sc.nextInt();long ans = 0;cnt[0] = 1;for (int i = 1; i <= n; ++ i) {sum[i] = sum[i - 1] + sc.nextInt(); //计算前缀和sum[i] %= k; //求出k的整数次倍剩下的数ans += cnt[sum[i]]; //相当于减去前面的余数,得出以i为终点的合法子序列的种数++ cnt[sum[i]]; //更新}System.out.println(ans);}
}
例题2、前缀和+哈希求最长个数平分子串:Leetcode 面试题 17.05 字母与数字
原题链接:https://leetcode-cn.com/problems/find-longest-subarray-lcci/
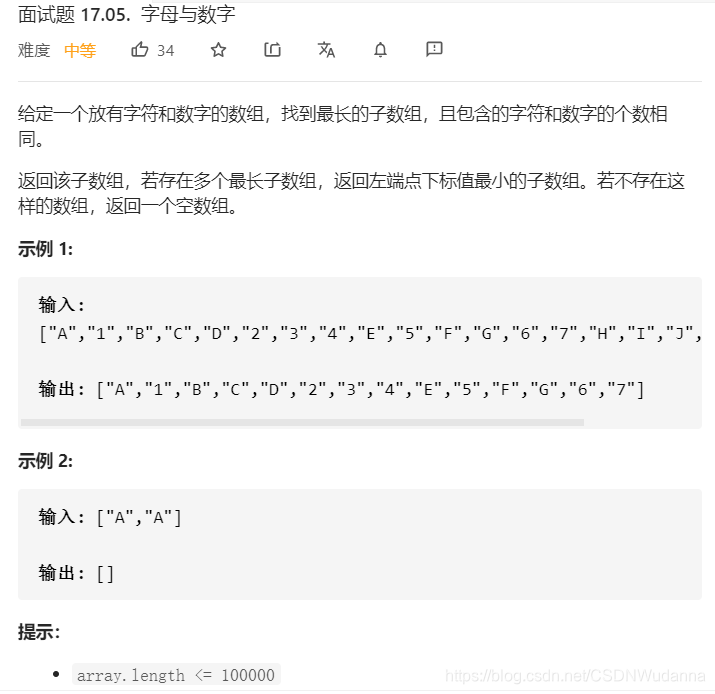
思路
字母+1,数字-1,获得array的前缀和数组arr,同时记录和维护当前的sum的最远索引位置,比如对于A 1 A A 1 1 A 1 1 1 A 1 1 A,可以获得前缀和数组:1 0 1 2 1 0 1 0 -1 -2 -1.
我们可以发现对于第一个A来说,能和它匹配的最长子数组是最后一个0的位置.
以此类比,假如当前位置是字母,其前缀和为a,那么最远能匹配的位置一定是最远的前缀和为a-1的地方;
反之,假如当前位置是数字,其前缀和为a,那么最远能匹配的位置一定是最远的前缀和为a+1的地方.
class Solution {
public:static const int N = 100000;int book[N * 2 + 20], arr[N + 20];vector<string> findLongestSubarray(vector<string>& array) {int num = 0, length = array.size();for (int i = 0; i < length; ++ i) {if (isNum(array[i][0])) -- num;else ++ num;book[num + N] = i;arr[i] = num;}vector<string> ans;int maxx = 0, l = -1, r = -1;for (int i = 0; i < length; ++ i) {if (isNum(array[i][0])) { int a = book[N + arr[i] + 1];if (a > i && a - i > maxx) {maxx = a - i;l = i, r = a;}}else {int a = book[N + arr[i] - 1];if (a > i && a - i > maxx) {maxx = a - i;l = i, r = a;}}}if (maxx == 0) return ans;else {for (int i = l; i <= r; ++ i) {ans.push_back(array[i]);}return ans;}}bool isNum(char c) {return c >= '0' && c <= '9';}
};
二、差分
1、一维差分
AcWing 797. 差分
原题链接:https://www.acwing.com/problem/content/799/

差分定义
首先给定一个原数组a:a[1], a[2], a[3]……a[n];
然后我们构造一个数组b : b[1] ,b[2] , b[3]…… b[i];
使得 a[i] = b[1] + b[2 ]+ b[3] +…… + b[i]
也就是说,a数组是b数组的前缀和数组,反过来我们把b数组叫做a数组的差分数组。
换句话说,每一个a[i]都是b数组中从头开始的一段区间和。
解法
给区间[l, r]中的每个数加上c:B[l] += c, B[r + 1] -= c
代码
#include<bits/stdc++.h>using namespace std;const int N = 100010;//add为差分数组,表示当前位置的变化
int nums[N], add[N];int main() {int n, m;cin >> n >> m;for (int i = 1; i <= n; ++ i) cin >> nums[i];while (m --) {int l, r, c;cin >> l >> r >> c;add[l] += c;add[r + 1] -= c;}for (int i = 1; i <= n; ++ i) {add[i] += add[i - 1];nums[i] += add[i];cout << nums[i] << " ";}return 0;
}
2、二维差分
AcWing 798. 差分矩阵
原题链接:https://www.acwing.com/problem/content/800/

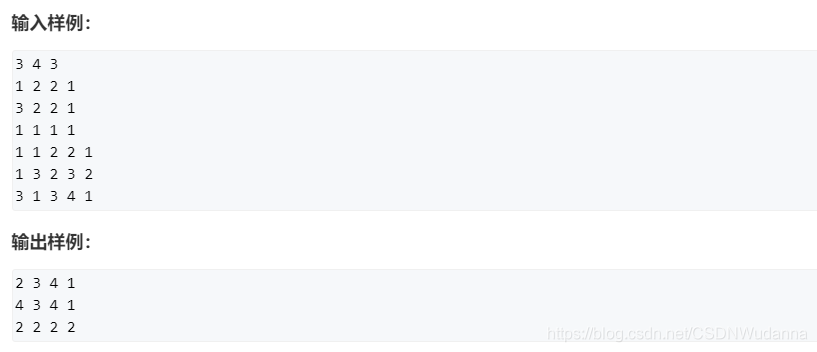
看代码应该就差不多了。
#include <bits/stdc++.h>using namespace std;const int N = 1010;int nums[N][N], add[N][N]; //add为差分矩阵void insert(int x1, int y1, int x2, int y2, int c) {add[x1][y1] += c;add[x1][y2 + 1] -= c;add[x2 + 1][y1] -= c;add[x2 + 1][y2 + 1] += c;
}int main() {int n, m, q;cin >> n >> m >> q;for (int i = 1; i <= n; ++ i) {for (int j = 1; j <= m; ++ j) {cin >> nums[i][j];}}while (q --) {int x1, y1, x2, y2, c;cin >> x1 >> y1 >> x2 >> y2 >> c;insert(x1, y1, x2, y2, c);}for (int i = 1; i <= n; ++ i) {for (int j = 1; j <= m; ++ j) {add[i][j] += add[i - 1][j] + add[i][j - 1] - add[i - 1][j - 1];nums[i][j] += add[i][j];cout << nums[i][j] << " ";}cout << endl;}return 0;
}
相关文章:

ACM - 其他算法 - 基础(前缀和 + 差分)
ACM- 其他算法 一、前缀和模板例题1、区间余数求K倍区间个数:AcWing 1230. K倍区间例题2、前缀和哈希求最长个数平分子串:Leetcode 面试题 17.05 字母与数字 二、差分1、一维差分2、二维差分 一、前缀和 模板 //一维前缀和 S[i] a[1] a[2] ... a[i] a[l] ... …...
备考大全》【冲刺10】《软考高项常见工具口语化解释》)
No.056<软考>《(高项)备考大全》【冲刺10】《软考高项常见工具口语化解释》
《软考高项常见工具口语化解释》 序号工具名称口语化属于哪个过程1模板、表格和标准就是用之前的项目的模版、表格、标准,结合本项目进行了修改,在编制一些计划、方案的时候就可以采用这个工具和技术。可以拿来就用的,节约时间、提高质量的。…...
:表分区和分库分表)
MySQL原理(九):表分区和分库分表
前言 上一篇介绍了 MySQL 的存储过程和触发器,这一篇将介绍表分区和分库分表相关的内容。 表分区 原本的表文件都是以完整的形式存储在磁盘中,而表分区则是指将一张表的数据拆分成多个磁盘文件,然后放到磁盘中存储。 做了表分区之后&…...
)
【Ehcache技术专题】「入门到精通」带你一起从零基础进行分析和开发Ehcache框架的实战指南(缓存查询-配置篇)
缓存查询 Ehcache中为我们提供了可以对Cache中缓存的元素进行查找的方式。其逻辑类似于SQL中的查找。通过给定各种限制条件,我们可以构造各种复杂的查询,然后返回结果集,也可以对查询进行分组和排序等。 使Cache可查询 Ehcache中的查询是针…...

MySQL基础(七)单行函数
1. 函数的理解 1.1 什么是函数 函数在计算机语言的使用中贯穿始终,函数的作用是什么呢?它可以把我们经常使用的代码封装起来,需要的时候直接调用即可。这样既提高了代码效率,又提高了可维护性。在 SQL 中我们也可以使用函数对检…...

Cy5.5-PEG-FA结构式 荧光Cy5.5标记聚乙二醇叶酸;PEG分子量2000,叶酸(-FA)基团可应用于靶向传递
Cy5.5-PEG-FA,Cy5.5-聚乙二醇-叶酸 中文名称:Cy5.5-聚乙二醇-叶酸 英文名称:Cy5.5-PEG-FA 溶剂:溶于水、氯仿,DMSO等常规性有机溶剂 性状:固体或粉末,取决于分子量 分子量:1k、…...
【微服务笔记23】使用Spring Cloud微服务组件从0到1搭建一个微服务工程
这篇文章,主要介绍如何使用Spring Cloud微服务组件从0到1搭建一个微服务工程。 目录 一、从0到1搭建微服务工程 1.1、基础环境说明 (1)使用组件 (2)微服务依赖 1.2、搭建注册中心 (1)引入…...
舞台特效-第14届蓝桥杯省赛Scratch初级组真题第2题
[导读]:超平老师的《Scratch蓝桥杯真题解析100讲》已经全部完成,后续会不定期解读蓝桥杯真题,这是Scratch蓝桥杯真题解析第131讲。 舞台特效,本题是2023年5月7日举行的第14届蓝桥杯省赛Scratch图形化编程初级组真题第2题…...
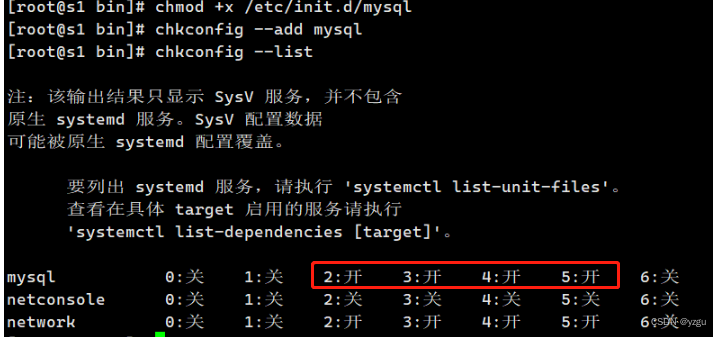
mysql 5.7.32安装及主从安装信息
最方便的 就是 直接使用docker容器 搭建一个比较方便 或者 直接使用yum源安装,说白了就是少踩坑。 或者 是直接使用 宝塔等工具帮忙,直接脚本跑 宝塔面板 - 简单好用的Linux/Windows服务器运维管理面板 以下是内网两台机器安装的方法 1: 下…...
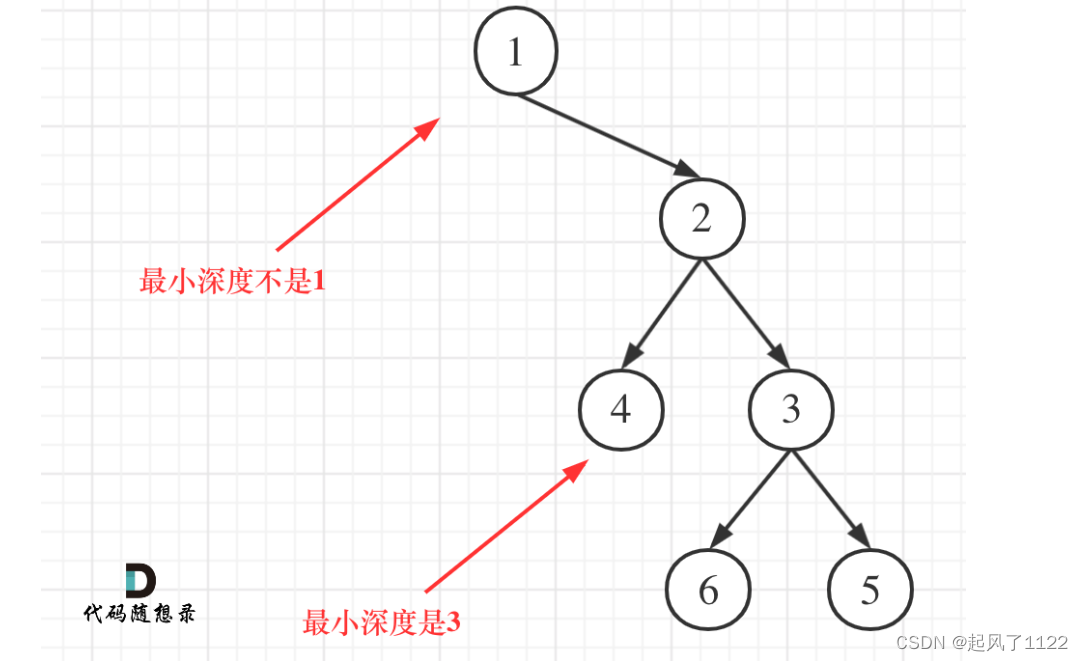
leecode111——二叉树最短路径
递归三部曲: 最小深度是从根节点到最近叶子节点的最短路径上的节点数量 (1)确定参数和返回值, 参数为传入根节点,再根据此遍历左右左右树的节点。返回最短路径,即int类型。 (2)确…...

Swift学习教程大纲
以下是Swift学习教程的大纲: 第一部分:基础知识 Swift简介 什么是Swift? Swift的历史和发展 Swift的特点和优势 开发环境的搭建 安装Swift编译器 配置开发环境 第一个Swift程序 Hello World程序 程序的结构 编译和运行程序 数据…...
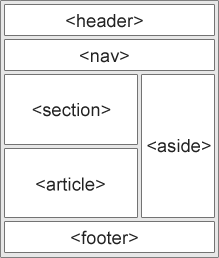
HTML 基础知识
HTML基础知识 1. VSCode的安装与配置 下载地址 https://code.visualstudio.com/ 安装插件 Live Server Auto Rename Tag 自动格式化 点击 settings,然后输入format,然后勾选上 Format On Save。 2. HTML 基础标签 2.1 文件结构 快捷键࿱…...

国考省考结构化面试:综合分析题,名言哲理(警句观点启示)、漫画反驳题等
国考省考结构化面试:综合分析题,名言哲理(警句观点启示)、漫画反驳题等 2022找工作是学历、能力和运气的超强结合体! 公务员特招重点就是专业技能,附带行测和申论,而常规国考省考最重要的还是申论和行测&a…...

【前端面经】CSS-浮动和清除浮动的方式
浮动和清除浮动的方式 在页面布局中,我们经常会用到浮动来实现一些特殊效果,但是浮动也会引起一些问题。在使用浮动布局时,我们需要清除浮动以避免出现布局问题。本文将介绍浮动的相关知识以及清除浮动的方式。 浮动 浮动是 CSS 中的一种布…...
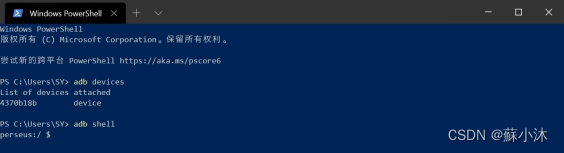
【Android取证篇】ADB版本更新详细步骤
【Android取证篇】ADB版本更新详细步骤 更新ADB版本,解决无法连接设备问题【蘇小沐】 ADB没有自动更新的命令,我们需要下载新的ADB进行替换更新。 1、ADB查找 打开任务管理器(快捷键shiftctrlEsc或WinX),在“详细信…...
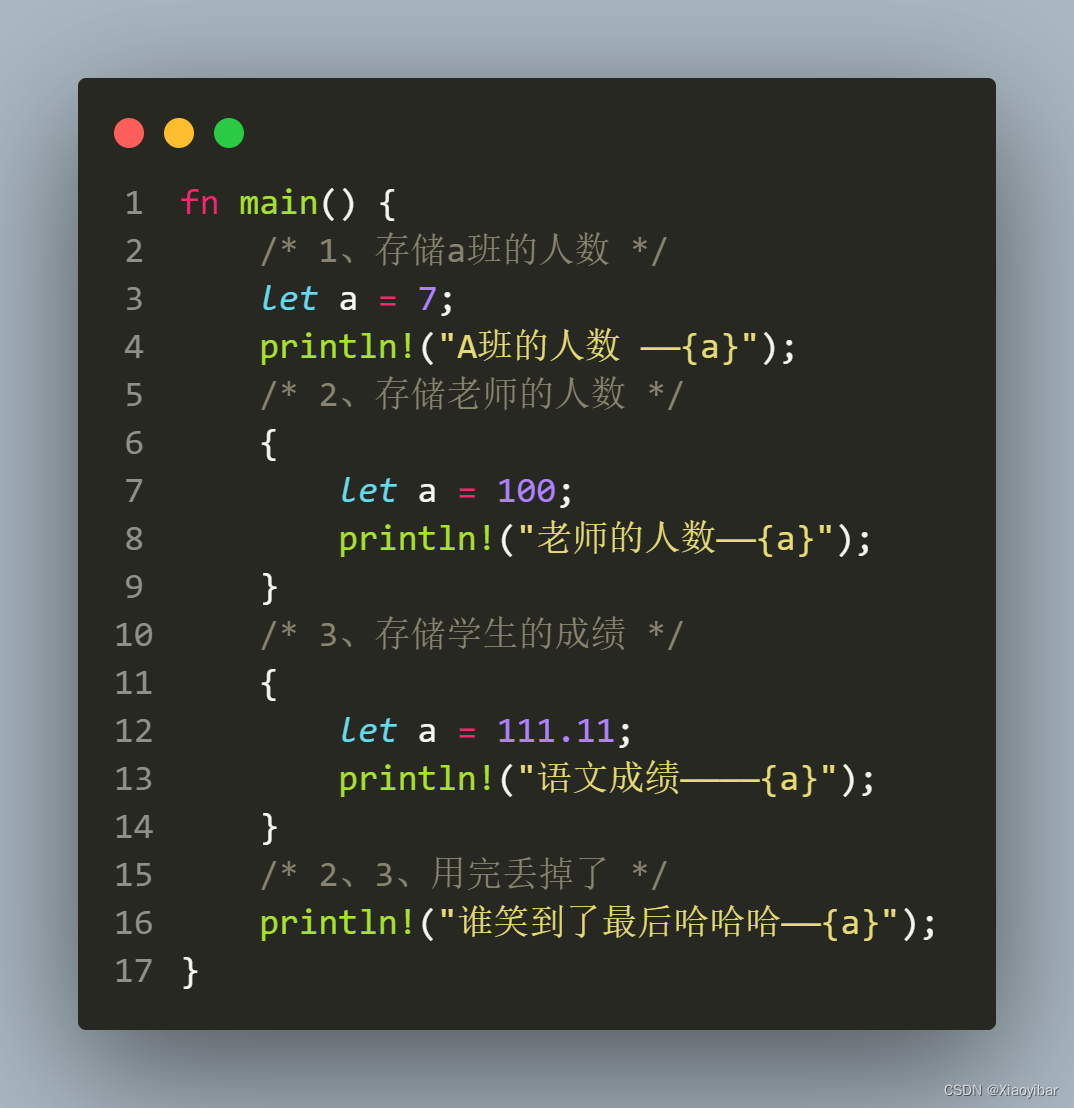
【rust】| 02——语法基础_变量(不可变?)和常量
系列文章目录 【rust】| 00——开发环境搭建 【rust】| 01——编译并运行第一个rust程序 【rust】| 02——语法基础_变量(不可变?)和常量 文章目录 1. 变量1.1 变量的定义1.2 试验变量的不可变特性 2. 常量2.1 常量的定义 3. 覆盖(同名变量)3.1 修改已定义变量的数据类型3.2 1…...

JavaScript实现在键盘输入按键,浏览器进行显示的代码
以下为实现在键盘输入按键,浏览器进行显示的代码和运行截图 目录 前言 一、在键盘输入按键,浏览器进行显示 1.1 运行流程及思想 1.2 代码段 1.3 JavaScript语句代码 1.4 运行截图 前言 1.若有选择,您可以在目录里进行快速查找…...
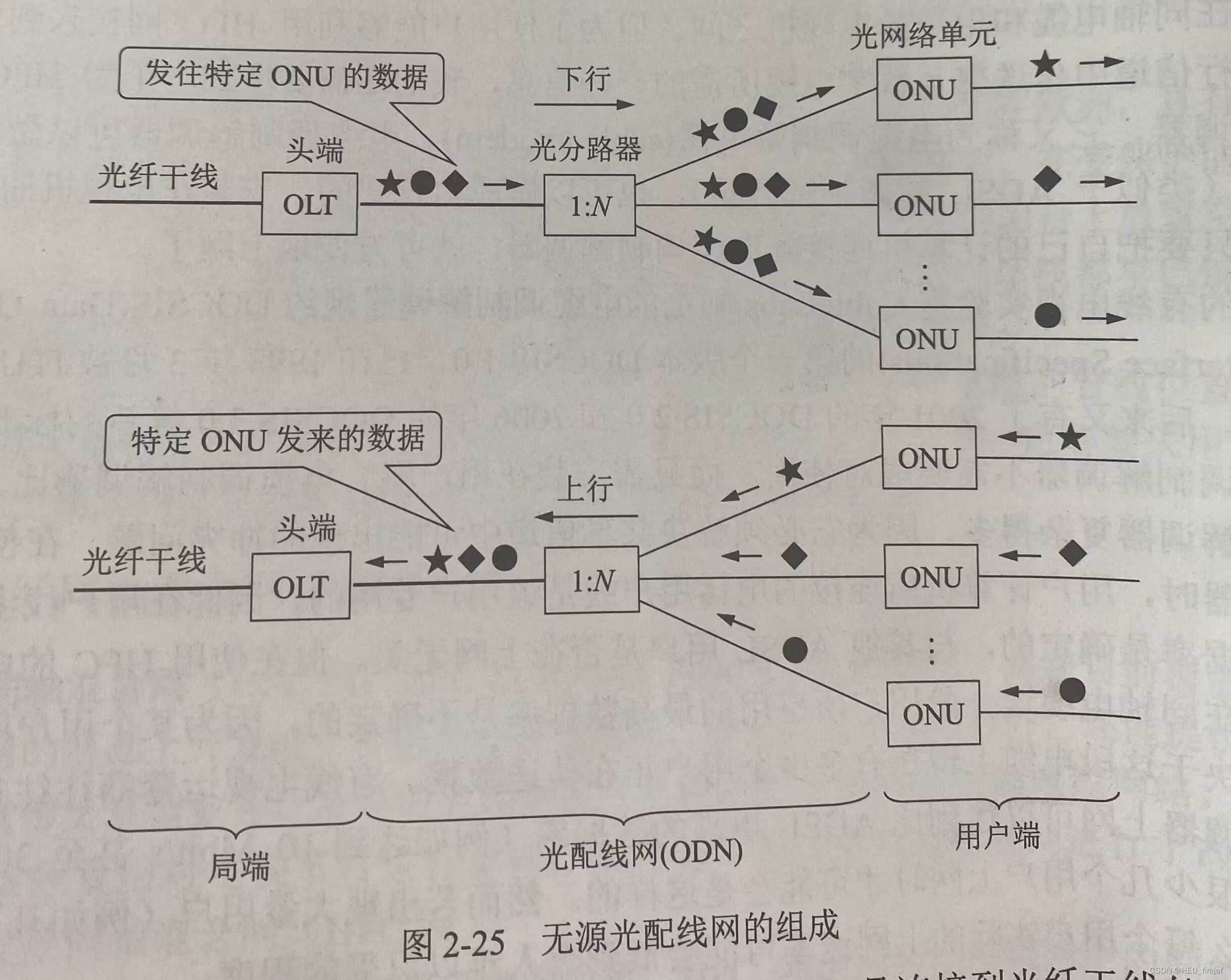
精炼计算机网络——物理层(二)
文章目录 前言2.4信道复用技术2.4.1 频分复用、时分复用和统计时分复用2.4.2 波分复用2.4.3 码分复用 2.5 数字传输系统2.6 带宽接入技术2.6.1 ADSL技术2.6.2 光纤同轴混合网(HFC网)2.6.3 FTTx技术 总结 前言 上篇文章,我们初步了解了物理层…...
ChatGPT直接访问,Edge浏览器-免费ChatGPT保姆级教程
人工智能大浪潮已经来临,对于ChatGPT,我觉得任何一个玩互联网的人,都应该重视起来,用起来。但是国内使用需要解决科学上网、注册、收费等繁琐问题。 所以,今天这篇文章就来推荐一个插件,无需任何繁琐操作&…...

1010. 总持续时间可被 60 整除的歌曲
题目: 在歌曲列表中,第 i 首歌曲的持续时间为 time[i] 秒。 返回其总持续时间(以秒为单位)可被 60 整除的歌曲对的数量。形式上,我们希望下标数字 i 和 j 满足 i < j 且有 (time[i] time[j]) % 60 0。 示例 1&a…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
