1099 Build A Binary Search Tree(超详细注解+38行代码)
分数 30
全屏浏览题目
作者 CHEN, Yue
单位 浙江大学
A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than or equal to the node's key.
- Both the left and right subtrees must also be binary search trees.
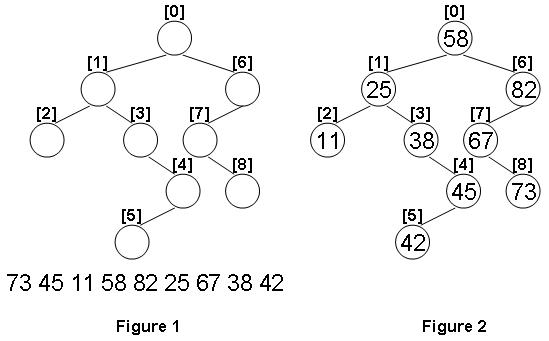
Given the structure of a binary tree and a sequence of distinct integer keys, there is only one way to fill these keys into the tree so that the resulting tree satisfies the definition of a BST. You are supposed to output the level order traversal sequence of that tree. The sample is illustrated by Figure 1 and 2.
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (≤100) which is the total number of nodes in the tree. The next N lines each contains the left and the right children of a node in the format left_index right_index, provided that the nodes are numbered from 0 to N−1, and 0 is always the root. If one child is missing, then −1 will represent the NULL child pointer. Finally N distinct integer keys are given in the last line.
Output Specification:
For each test case, print in one line the level order traversal sequence of that tree. All the numbers must be separated by a space, with no extra space at the end of the line.
Sample Input:
9
1 6
2 3
-1 -1
-1 4
5 -1
-1 -1
7 -1
-1 8
-1 -1
73 45 11 58 82 25 67 38 42
Sample Output:
58 25 82 11 38 67 45 73 42
代码长度限制
16 KB
时间限制
200 ms
内存限制
64 MB
#include<bits/stdc++.h>
using namespace std;
const int N=105;
int l[N],r[N];//分别保存当前结点的左右孩子结点
int a[N],res[N];//a[N]保存中序序列的值,res[N]保存每个结点对应的值
void inorder(int root,int &k){//中序遍历结点并将中序序列按顺序填入各节点
if(l[root]!=-1)inorder(l[root],k);//若有左孩子,递归遍历
res[root]=a[k++];//将值保存在对应结点的位置
if(r[root]!=-1)inorder(r[root],k);//若有有孩子,递归遍历
return ;
}
void levelorder(int root){//层序遍历
queue<int>q;
q.push(root);//根结点入队
while(q.size()){//队列中有元素
int f=q.front();//获得队头元素
q.pop();//出队
if(l[f]!=-1)q.push(l[f]);//若队头结点有左孩子,则将左孩子入队
if(r[f]!=-1)q.push(r[f]);//若队头结点有右孩子,则将右孩子入队
cout<<res[f];//输出队头结点对应的值
if(q.size())cout<<' ';//若队列还有元素输出空格,最后一个元素不用输出
}
}
int main(){
int n;
cin>>n;
for(int i=0;i<n;i++){//从第0个结点到第n-1个结点,保存各结点的左右孩子结点
int lchild,rchild;
cin>>lchild>>rchild;
l[i]=lchild,r[i]=rchild;
}
for(int i=0;i<n;i++)cin>>a[i];//输入给定初始序列
sort(a,a+n);//从小到大排序,即中序序列
int k=0;//用于记录当前的结点
inorder(0,k);//0表示根结点
levelorder(0);//层序遍历
return 0;
}
相关文章:

1099 Build A Binary Search Tree(超详细注解+38行代码)
分数 30 全屏浏览题目 作者 CHEN, Yue 单位 浙江大学 A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties: The left subtree of a node contains only nodes with keys less than the nodes key.The right subtree…...
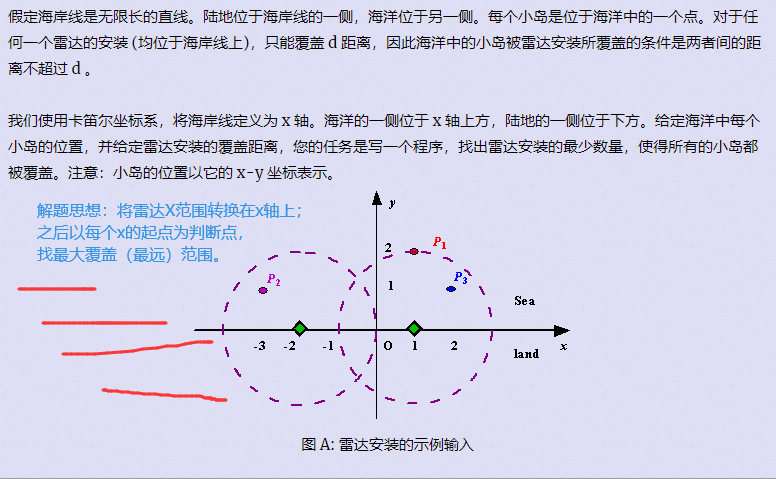
[刷题]贪心入门
文章目录 贪心区间问题区间选点区间合并区间覆盖 哈夫曼树(堆)合并果子 排序不等式排队打水 绝对值不等式货仓选址 推出来的不等式耍杂技的牛 以前的题 贪心 贪心:每一步行动总是按某种指标选取最优的操作来进行, 该指标只看眼前&…...
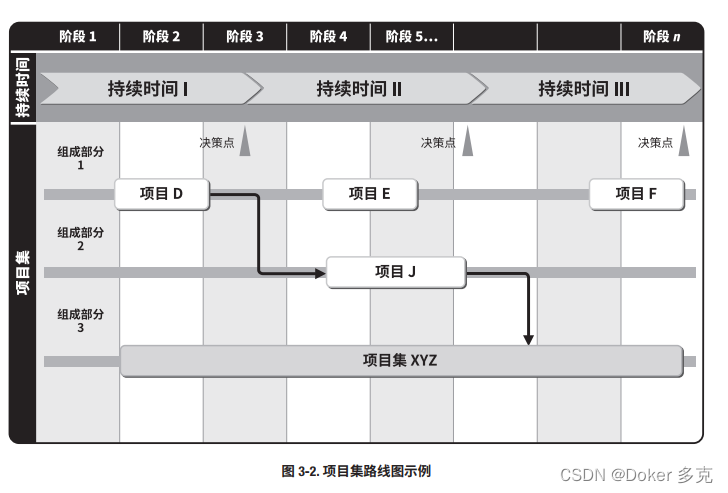
项目集战略一致性
项目集战略一致性是识别项目集输出和成果,以便与组织的目标和目的保持一致的绩效领域。 本章内容包括: 1 项目集商业论证 2 项目集章程 3 项目集路线图 4 环境评估 5 项目集风险管理战略 项目集应与组织战略保持一致,并促进组织效益的实现。为…...
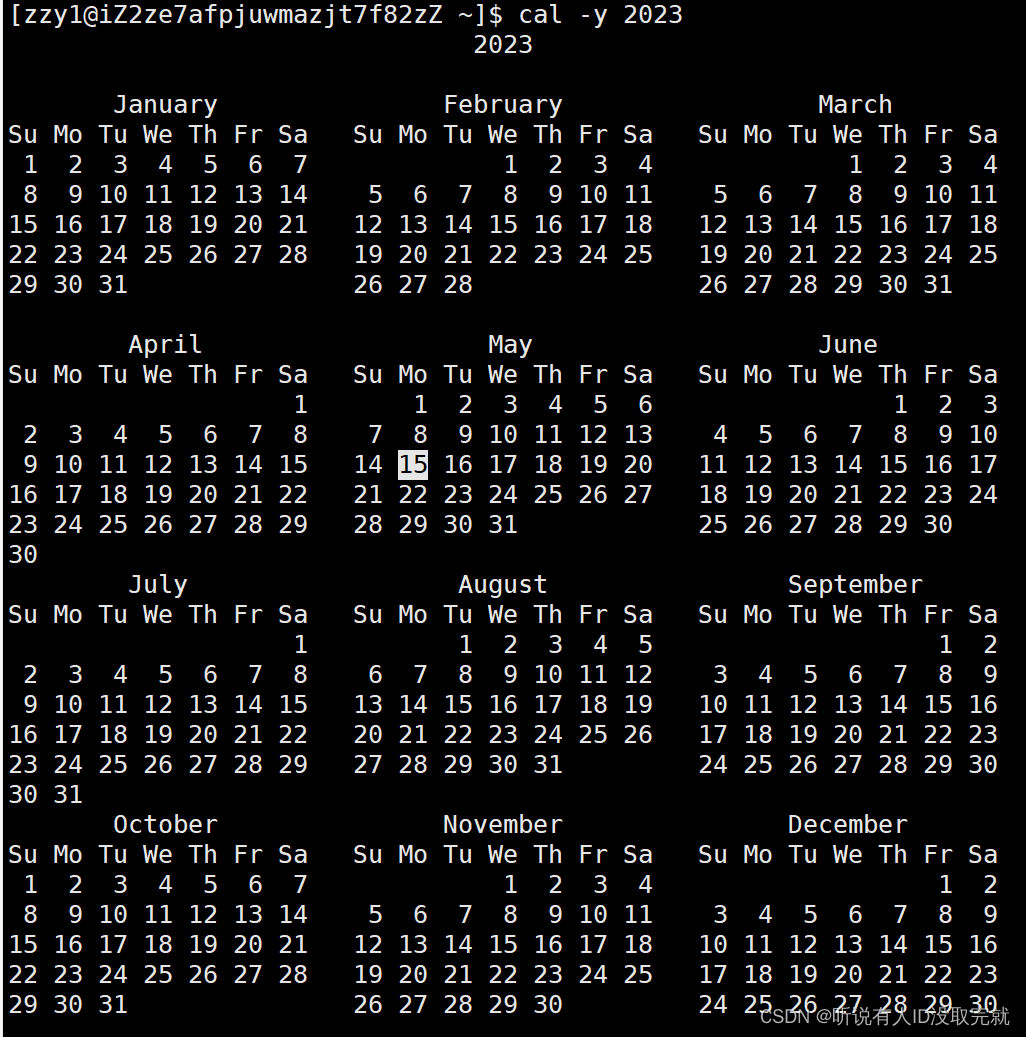
Linux学习 Day3
目录 1. 时间相关的指令 2. cal指令 3. find指令:(灰常重要) -name 4. grep指令 5. zip/unzip指令 6. tar指令(重要):打包/解包,不打开它,直接看内容 7. bc指令 8. uname –…...

前端开发推荐vscode安装什么插件?
前言 可以参考一下下面我推荐的插件,注意:插件的目的是用于提高开发的效率,节约开发的时间,像类似检查一些bug、拼写错误等这些可以使用插件快速的识别,避免在查找错误上浪费过多的时间,但切记不要过度依赖…...

如何打造完整的客户服务体系?
对于企业来说,提供优质的客户服务是保持竞争力和赢得市场份额的关键因素之一。一个高效、专业、人性化的客户服务体系,对于企业吸引和留住客户,提升品牌声誉,甚至增加销售额都有着不可忽视的作用。本文将从多个方面来阐述如何打造…...

裸奔时代,隐私何处寻?
随着互联网的普及,人工智能时代的大幕初启,数据作为人工智能的重要支撑,数据之争成为“兵家必争之地”,随之而来的就是,各种花式手段“收割”个人信息,用户隐私暴露程度越来越高,隐私保护早已成…...
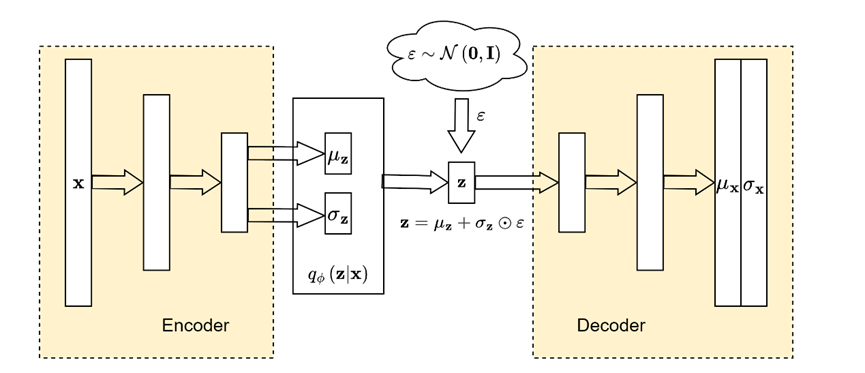
从期望最大化(EM)到变分自编码器(VAE)
本文主要记录了自己对变分自编码器论文的理解。 Kingma D P, Welling M. Auto-encoding variational bayes[J]. arXiv preprint arXiv:1312.6114, 2013. https://arxiv.org/abs/1312.6114 1 带有潜在变量的极大似然估计 假设我们有一个有限整数随机数发生器 z ∼ p θ ( z ) …...

【数学杂记】表达式中的 s.t. 是什么意思
今天写题的时候遇见了这个记号:s.t.,查了一下百度。 s.t.,全称 subject to,意思是“使得……满足”。 比如这个: 意思是存在 i i i,使得 i i i 满足 A i ≠ B i A_i\neq B_i AiBi. 运用这个记号…...

flink watermark介绍及watermark的窗口触发机制
Flink的三种时间 在谈watermark之前,首先需要了解flink的三种时间概念。在flink中,有三种时间戳概念:Event Time 、Processing Time 和 Ingestion Time。其中watermark只对Event Time类型的时间戳有用。这三种时间概念分别表示: …...

Spring Cloud: 云原生微服务实践
文章目录 1. Spring Cloud 简介2. Spring Cloud Eureka:服务注册与发现在Spring Cloud中使用Eureka 3. Spring Cloud Config:分布式配置中心在Spring Cloud中使用Config 4. Spring Cloud Hystrix:熔断器在Spring Cloud中使用Hystrix 5. Sprin…...

存bean和取bean
准备工作存bean获取bean三种方式 准备工作 bean:一个对象在多个地方使用。 spring和spring boot:spring和spring boot项目;spring相当于老版本 spring boot本质还是spring项目;为了方便spring项目的搭建;操作起来更加简单 spring…...

39. 组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。 candidates 中的 同一个 数字可以 无限制重复被选取 。如…...

100行以内Python能做那些事
Python100 找到一个很好的python教程分享出来---->非本人 B站视频连接 100行以内的Pyhton代码可以做哪些有意思的事 按照难度1-5颗星,分为五个文件夹 希望大家可以补充 关于运行环境的补充 Python3.7 Pycharm社区版2019 关于用到的Python库,有些是自带的&am…...

Android 电源键事件流程分析
Android 电源键事件流程分析 电源按键流程处理逻辑在 PhoneWindowManager.java类中的 dispatchUnhandledKey 方法中 frameworks/base/services/core/java/com/android/server/policy/PhoneWindowManager.java从dispatchUnhandledKey方法开始分析 Overridepublic KeyEvent dis…...

游戏搬砖简述-1
游戏搬砖是一种在游戏中通过重复性的任务来获取游戏内货币或物品的行为。这种行为在游戏中非常普遍,尤其是在一些MMORPG游戏中。虽然游戏搬砖看起来很无聊,但是它确实是一种可以赚钱的方式,而且对于一些玩家来说,游戏搬砖也是一种…...

多线程基础总结
1. 为什么要有多线程? 线程:线程是操作系统能够进行运算调度的最小单位。它被包含在进程之中,是进程中实际运行单位。 进程:进程是程序的基本执行实体。 什么是多线程? 有了多线程,我们就可以让程序同时做…...
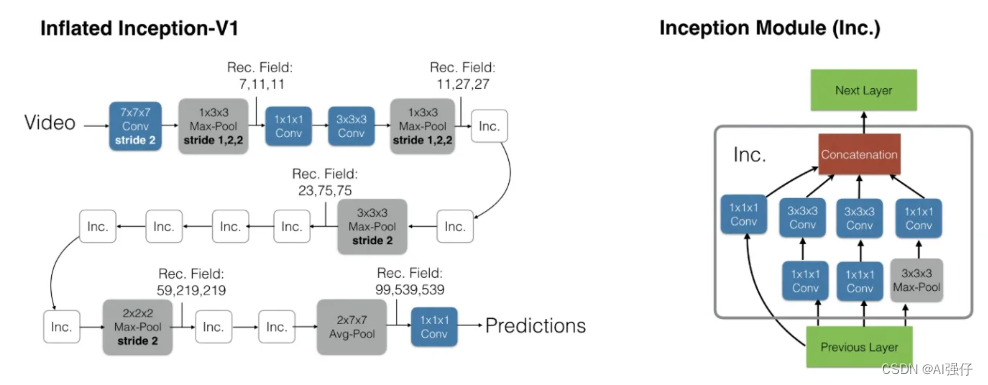
视频理解AI模型分类与汇总
人工智能领域视频模型大体也经历了从传统手工特征,到卷积神经网络、双流网络(2014年-2017年)、3D卷积网络、transformer的发展脉络。为了时序信息,有的模型也结合用LSTM。 视频的技术大多借鉴图像处理技术,只是视频比…...
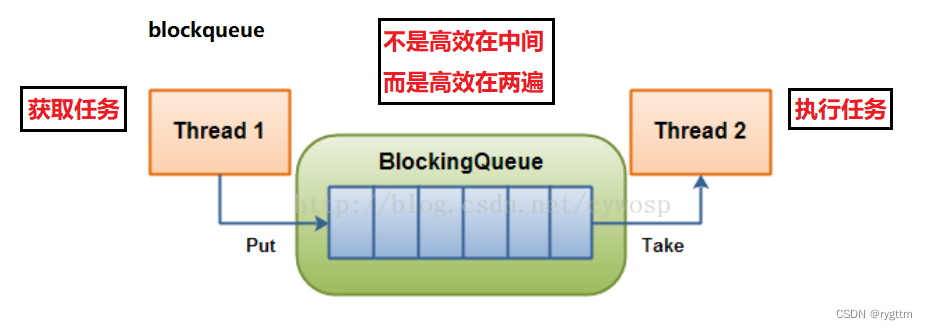
【Linux】多线程 --- 线程同步与互斥+生产消费模型
人生总是那么痛苦吗?还是只有小时候是这样? —总是如此 文章目录 一、线程互斥1.多线程共享资源访问的不安全问题2.提出解决方案:加锁(局部和静态锁的两种初始化/销毁方案)2.1 对于锁的初步理解和实现2.2 局部和全局锁…...

17.模型的定义
学习要点: 1.默认设置 2.模型定义 本节课我们来开始学习数据库的模型部分的定义和默认值的设置。 一.默认设置 1. 框架可以使用 Eloquent ORM 进行数据库交互,也就是关系对象模型; 2. 在数据库入门阶段,我们已经创建了…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...
