数据结构学习分享之树的介绍
💓博主CSDN主页:杭电码农-NEO💓
⏩专栏分类:数据结构学习分享⏪
🚚代码仓库:NEO的学习日记🚚
🌹关注我🫵带你了解更多数据结构的知识
🔝🔝

数据结构第六课
- 1. 前言🚩
- 2. 树的概念以及结构🚩
- 2.1 树的概念🏁
- 2.2 树的相关概念🏁
- 2.3 树的表示(代码实现)🏁
- 3. 二叉树的概念以及结构🚩
- 3.1 二叉树概念🏁
- 3.2 特殊的二叉树🏁
- 3.3 二叉树的性质🏁
- 3.4 二叉树的存储结构🏁
- 4. 总结🚩
1. 前言🚩
前面我们学的都是链式结构或数组这种线性结构,今天我们正式开始学习"树"这个结构.树涉及的问题有很多,包括普通树,二叉树,二叉树又分完全二叉树和非完全二叉树,而我们要掌握的结构"堆"其本质就是一种完全二叉树, 所以在开始讲堆之前,我们应该先了解一些树相关的知识
2. 树的概念以及结构🚩
2.1 树的概念🏁
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的.
- 有一个特殊的结点,称为根结点,根节点没有前驱结点.
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 树是递归定义的。
平平无奇的一棵树:
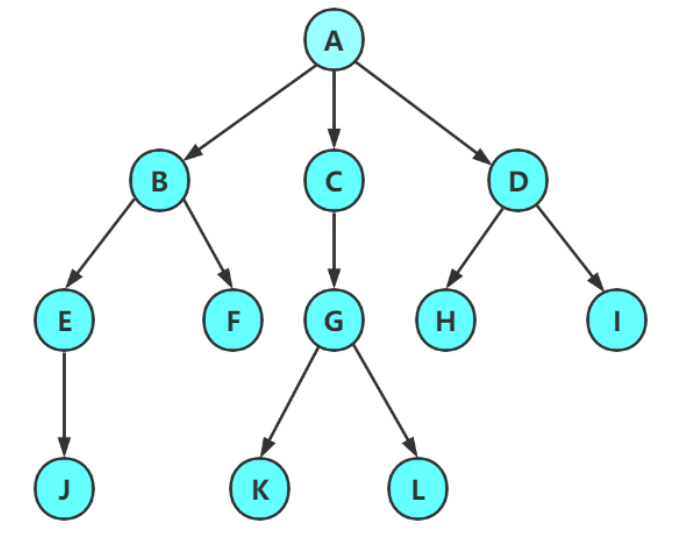
注意,子树之间是不能又交集的,否则就不能称为树结构:
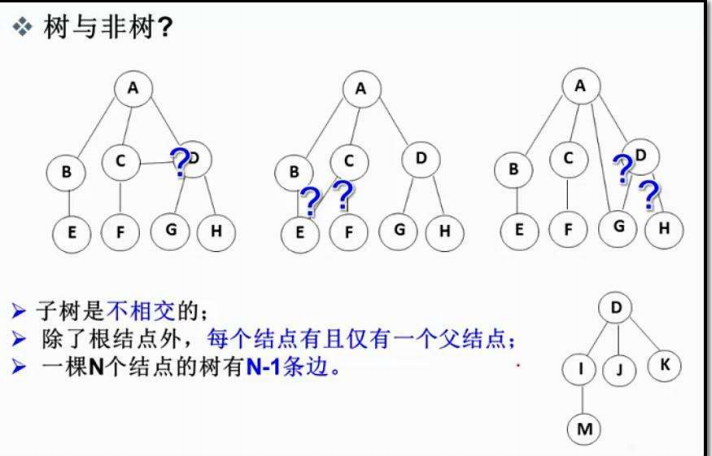
2.2 树的相关概念🏁
有一些专有名词需要我们了解,我这里给出一个图方便理解:
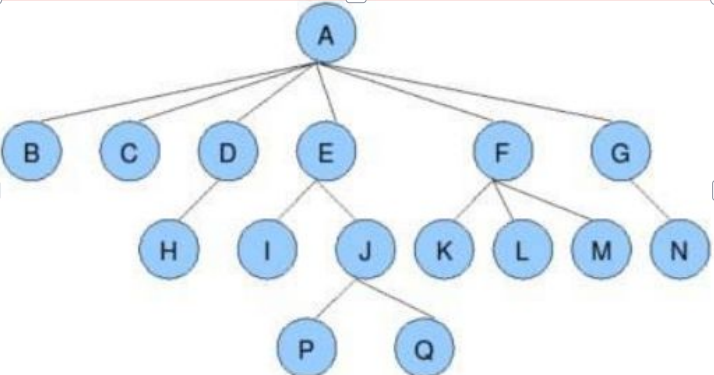
- 节点的度:一个节点含有的子树的个数称为该节点的度;如上图:A的为6
- 叶节点或终端节点:度为0的节点称为叶节点;如上图:B、C、H、I…等节点为叶节点
- 非终端节点或分支节点:度不为0的节点;如上图:D、E、F、G…等节点为分支节点
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;如上图:A是B的父节点孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;如上图:B是A的孩子节点
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;如上图:B、C是兄弟节点
- 树的度:一棵树中,最大的节点的度称为树的度;如上图:树的度为6
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次;如上图:树的高度为4
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
- 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
- 森林:由m(m>0)棵互不相交的树的集合称为森林;
这里我将常见的并且用的比较多的概念换了一个颜色
2.3 树的表示(代码实现)🏁
表示树形结构有很多种方式,比如:
- 方法一:提前知道树的度数为N
struct TreeNode
{int data;struct TreeNode* subs[N];//存储此节点的孩子,最多有N个孩子
}
这里前提我们知道树的度,也就是一个节点最大的孩子树,我们可以设计一个结构体,里面存储当前节点要存储的值,并且在结构体中定义一个结构体数组来存储此节点的孩子.
这里表示树的结构的方式有很多,我就不做一一介绍,接下来介绍一个最屌的结构也是最常用的结构:左孩子右兄弟法!
我们用这个树来举个例子:
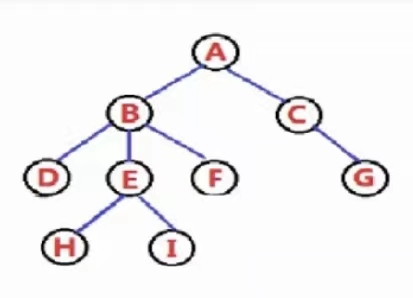
typedef int DataType;
struct Node
{struct Node* firstChild1; // 第一个孩子结点struct Node* NextBrother; // 指向其下一个兄弟结点DataType data; // 结点中的数据域
}
这种结构属于是牛人才能想出来!这里我们画图理解一下:
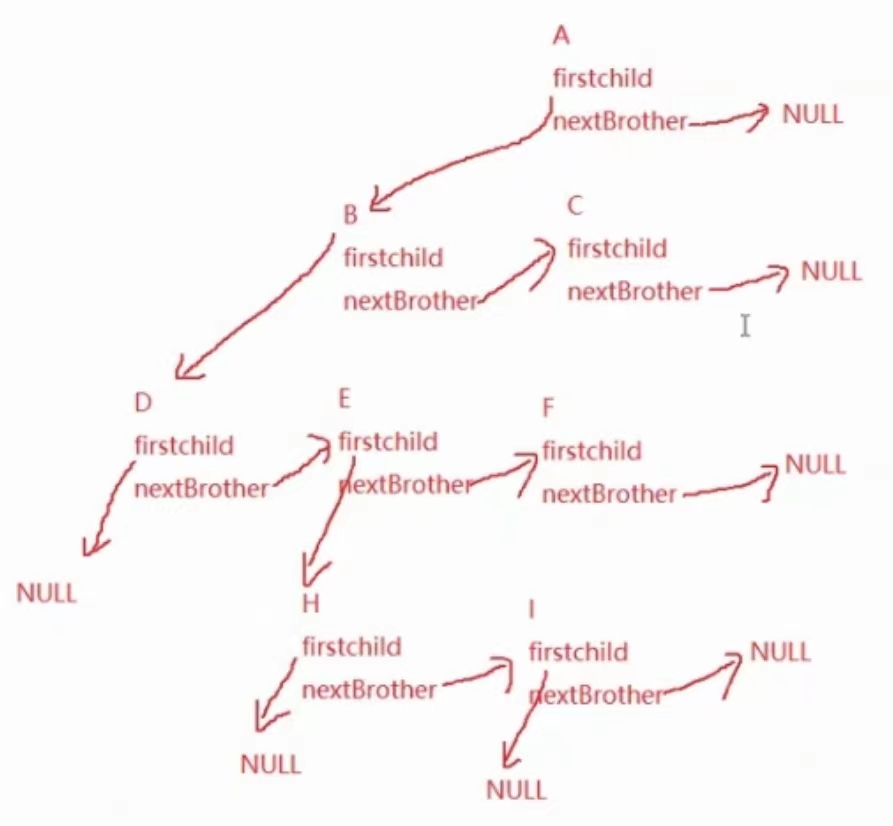
这样我们就可以依次把所有节点都遍历一遍了
3. 二叉树的概念以及结构🚩
数中这么复杂的结构,最常用的还是二叉树,这里就引出二叉树的概念
3.1 二叉树概念🏁
一棵二叉树是结点的一个有限集合,该集合:
-
或者为空
-
由一个根节点加上两棵别称为左子树和右子树的二叉树组成
-
二叉树不存在度大于2的结点
-
二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:(这些情况以及这些情况的组合情况都称为二叉树)
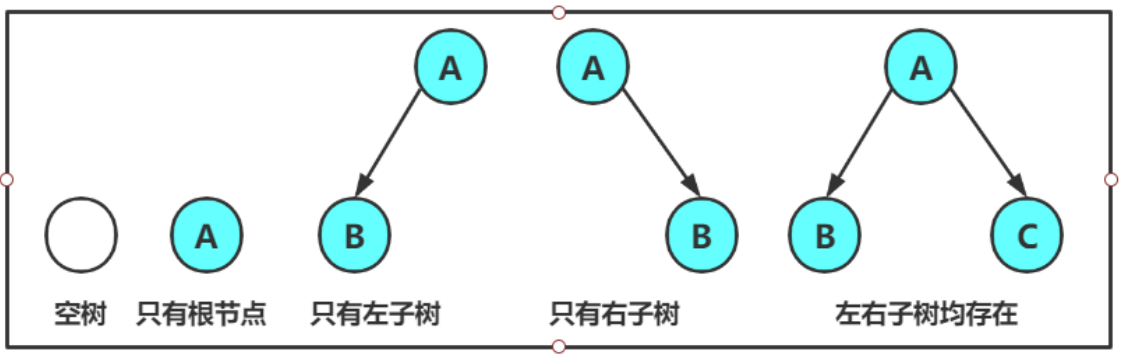
有人说可以用下面这张图辨别一个人是不是程序员,如果他看见图的第一眼想到的是:这不就是个满二叉树嘛,那么他大概率是程序员!

3.2 特殊的二叉树🏁
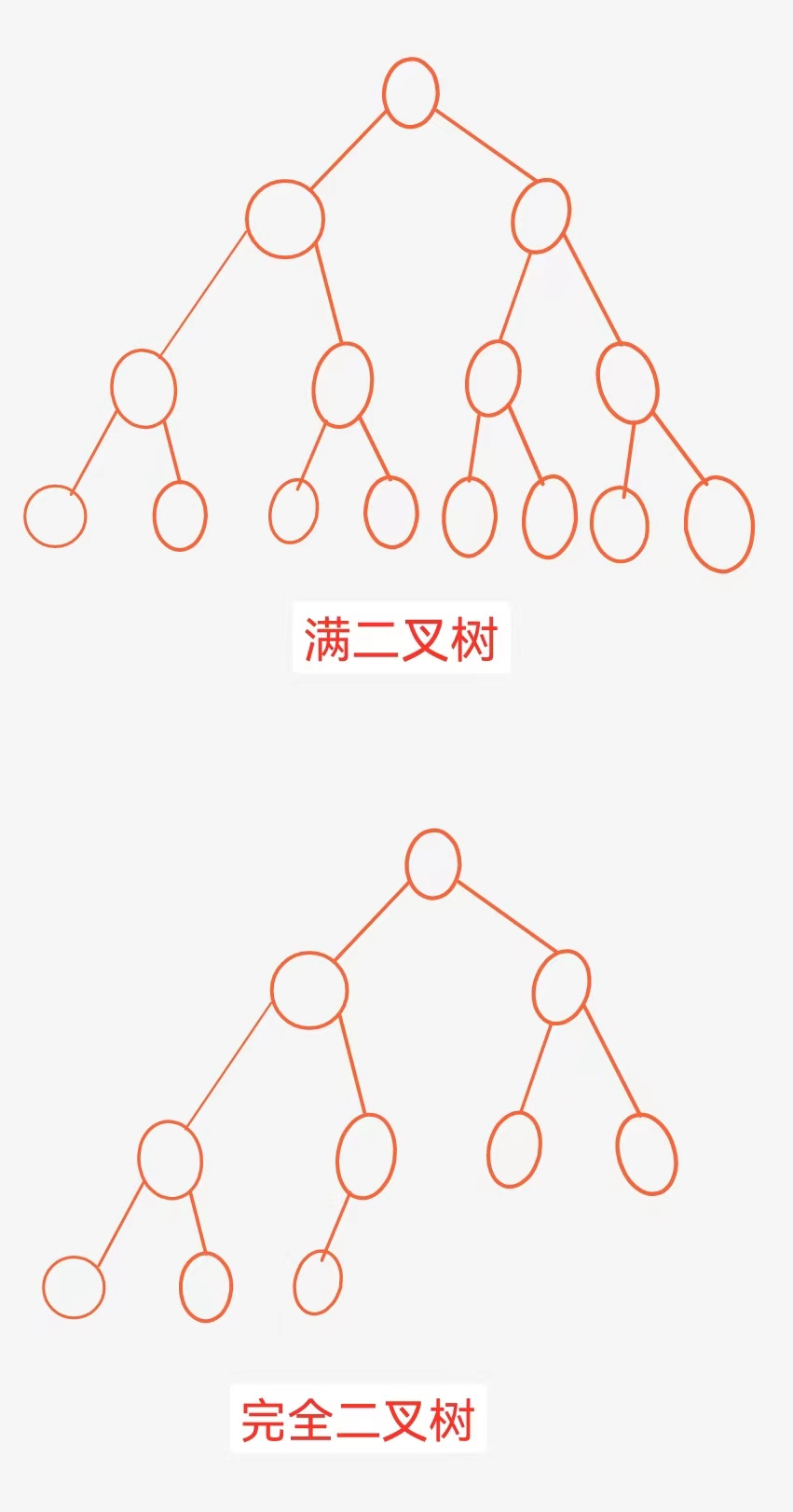
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是
说,如果一个二叉树的层数为K,且结点总数是2k-1 ,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K
的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对
应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
3.3 二叉树的性质🏁
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2i-1个结点.
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2h-1 .
- 对任何一棵二叉树, 如果度为0其叶结点个数为n0 , 度为2的分支结点个数为n2 ,则有 n0=n2 +1
- 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=log2(n+1) .
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
- 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
- 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩
- 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
因为这一章节是全新的内容,所以定义和性质很多,请大家要耐心阅读!
3.4 二叉树的存储结构🏁
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构:
- 顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空
间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺
序存储在物理上是一个数组,在逻辑上是一颗二叉树。
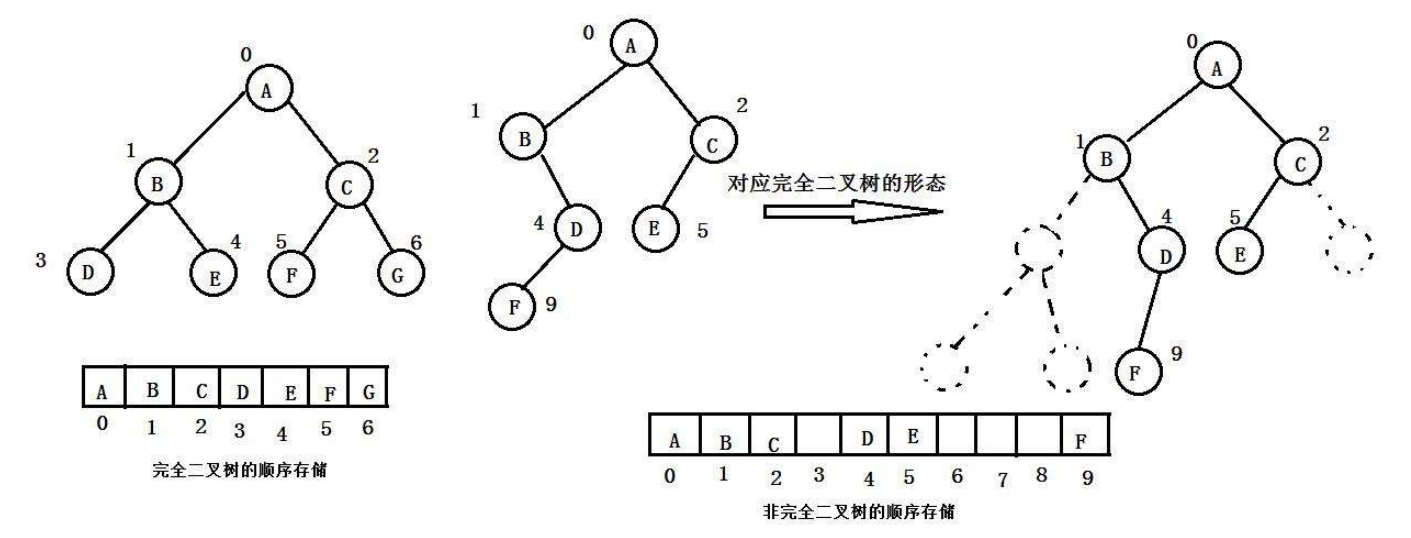 这里非完全二叉树存储在顺序结构中时,数组中有空元素,而完全二叉树存储时没有空元素
这里非完全二叉树存储在顺序结构中时,数组中有空元素,而完全二叉树存储时没有空元素
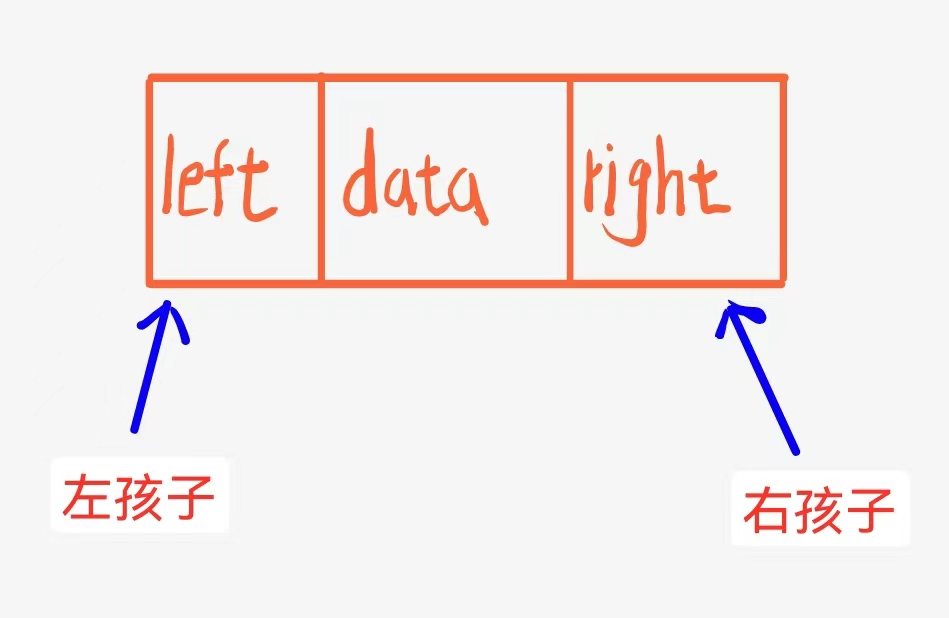
- 链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是
链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所
在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,后面课程
学到高阶数据结构如红黑树等会用到三叉链。
我们可以发现,非完全二叉树不适合用数组的方式来存储,然而我们的完全二叉树(包括满二叉树)就非常适合用数组的形式存储,因为它的物理存储结构是连续的,不会在数组中留空格
4. 总结🚩
. 这篇文章主要带大家了解一下树的相关知识,为我们后面学习二叉树和堆打好基础,其实堆的本质就是一颗完全二叉树,所以我们实现堆时就是用数组的结构来实现的,而我们的非完全二叉树即用链式结构来实现的.这些内容我下一篇文章为大家讲解
相关文章:

数据结构学习分享之树的介绍
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:数据结构学习分享⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你了解更多数据结构的知识 🔝🔝 数据结构第六课 1. 前言&a…...
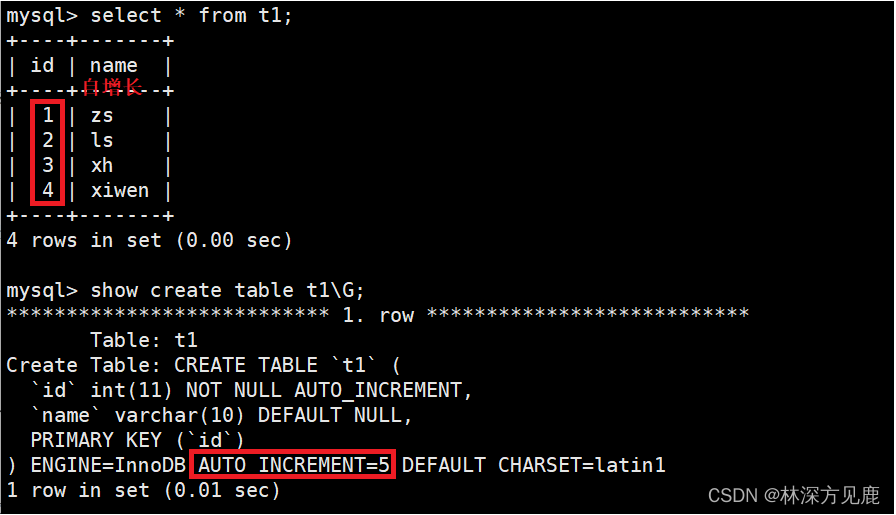
MySQL数据库基础2
文章目录 数据类型表的约束 数据类型 1、数值类型:BIT、TINYINT、BOOL、SMALLINT、INT、BIGINT、FLOAT[(M,D)]、DOUBLE[(M,D)]、DECIMAL[(M,D)] FLOAT[(M,D)]:占用四个字节,M表示显示位数,D表示小数位数,精度保证&am…...
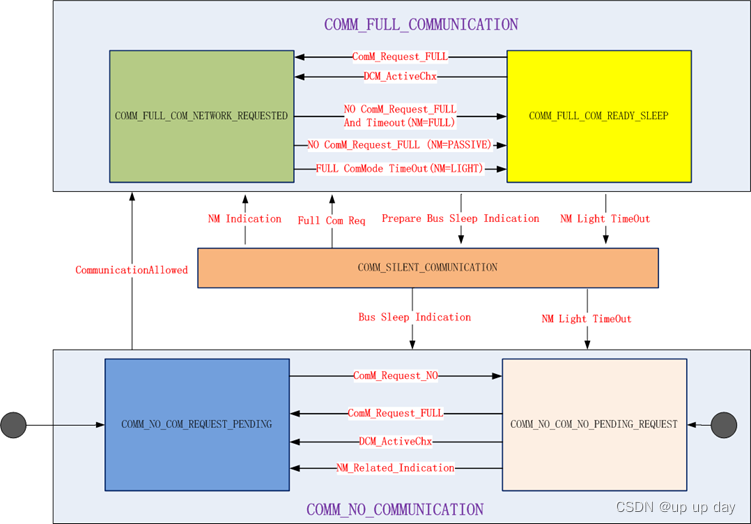
AutoSAR PNC和ComM
文章目录 PNC和ComMPNC管理NM PDU结构及PNC信息位置如何理解节点关联PNCPNC状态管理 ComM 通道状态管理 PNC和ComM PNC 和 ComM层的Channel不是一个概念,ComM的Channel对应具体的物理总线数。 在ComM模块中,一个Channel可以对应一个PNC,也可…...

Android studio Camera2实现的详细流程
流程 一、获取CameraManager实例二、获取可用的相机列表三、选择一个相机并打开它四、创建一个CaptureRequest.Builder对象五、设置CaptureRequest.Builder对象的参数六、创建一个CaptureSession对象七、开始预览 代码示例 一、获取CameraManager实例 CameraManager manager (…...

阿里云数据库ClickHouse产品和技术解读
摘要:社区ClickHouse的单机引擎性能十分惊艳,但是部署运维ClickHouse集群,以及troubleshoot都不是很好上手。本次分享阿里云数据库ClickHouse产品能力和特性,包含同步MySQL库、ODPS库、本地盘及多盘性价比实例以及自建集群上云的迁…...
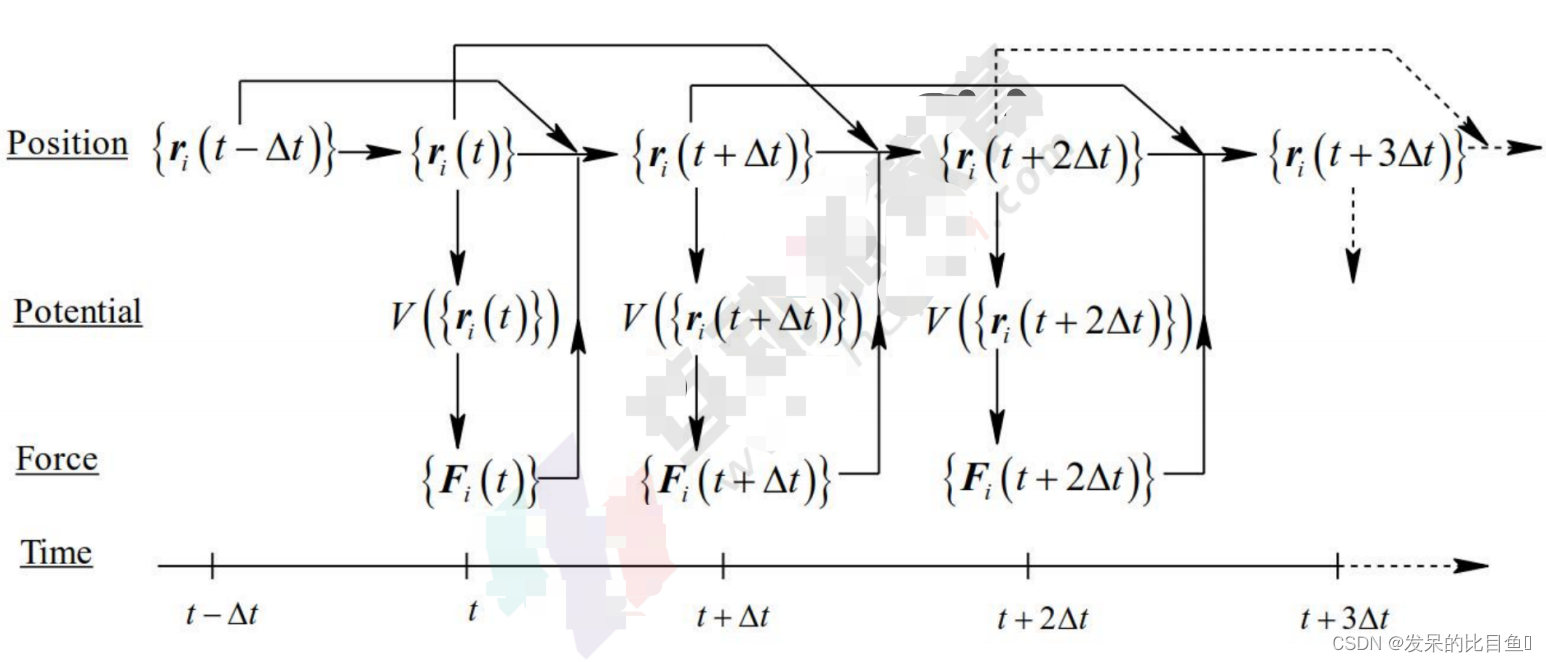
分子动力学基础知识
分子动力学基础知识 目前主要存在两种基本模型:其一为量子统计力学, 其二为经典统计力学。 量子统计力学 基于量子力学原理, 适用 于微观的, 小尺度, 短时 间的模拟,可以描述电子 的结构分布,原子间的成 键断键等化学性质。 经典纭计力学…...

USB转UART转串口芯片 GP232RNL国产低成本替代FT232RL/FT232RNL
近期收到很多人咨询FT232RL跟新版FT232RNL两者有什么区别,实际上就是内部做了一点升级,FT232RNL支持Windows11系统,参数并没有改动,完全可以直接替换使用。 今天小编给大家讲讲FT232RNL国产低成本替代芯片–GP232RNL GP232RNL 是…...
第03讲:SpringCloudStream实现分布式事务
需求分析 本案例是通过一个发送短信验证码的功能来实验MQ发送消息时实现分布式事务,思路分析如下 消息生产者生产发送验证码的半消息 生产者执行本地事务(将验证码保存到数据库),并记录事务的ID,如果整个过程不出现异…...
【从零开始学Skynet】高级篇(一):Protobuf数据传输
1、什么是Protobuf Protobuf是谷歌发布的一套协议格式,它规定了一系列的编码和解 码方法,比如对于数字,它要求根据数字的大小选择存储空间,小于等于15的数字只用1个字节来表示,大于15的数用2个字节表示,以此…...

快速入门Lombok
Lombok是一个Java库,可以通过注解的方式来简化Java代码,它可以自动生成Getter、Setter、构造函数等代码,从而减少重复的模板代码。下面是Lombok的使用详情: 1. 添加Lombok依赖 在使用Lombok之前,我们需要先添加Lombo…...
Linux 常见命令与常见问题解决思路
Linux 常见命令 Linux 基础命令目录相关查看文件(日志)查看普通的文件查看压缩的文件 解压压缩Linux 系统调优topvmstatpidstatps vi/vim 编辑文件查找文件属性相关定时任务scp 复制文件和目录awk 分隔cutsort 与 uniq常见问题处理思路CPU 高系统平均负载…...

用GPT-4 写2022年天津高考作文能得多少分?
正文共 792 字,阅读大约需要 3 分钟 学生必备技巧,您将在3分钟后获得以下超能力: 积累作文素材 Beezy评级 :B级 *经过简单的寻找, 大部分人能立刻掌握。主要节省时间。 推荐人 | Kim 编辑者 | Linda ●图片由Lexica …...

Django如何把SQLite数据库转换为Mysql数据库
大部分新手刚学Django开发的时候默认用的都是SQLite数据库,上线部署的时候,大多用的却是Mysql。那么我们应该如何把数据库从SQLite迁移转换成Mysql呢? 之前我们默认使用的是SQLite数据库,我们开发完成之后,里面有许多数…...

使用apisix代理静态文件
前言 最近公司考虑用apisix作为公司网关并且部署到k8s上,我这边收到一个小任务:使用apisix代理静态文件 通过apisix官网了解到它构建于 NGINX ngx_lua 的技术基础之上,所以按理应该和nginx代理静态资源是一样的。因为是通过docker容器部署…...
)
[元带你学NVMe协议] NVMe1.4 多路径(Multipathing)
声明 主页:元存储的博客_CSDN博客 依公开知识及经验整理,如有误请留言。 个人辛苦整理,付费内容,禁止转载。 内容摘要 全文9100字, 主要内容 目录 前言 1 多路径(Multipathing)概念...

Elasticsearch:如何使用自定义的证书安装 Elastic Stack 8.x
在我之前的文章 “如何在 Linux,MacOS 及 Windows 上进行安装 Elasticsearch”,我详细描述了如何在各个平台中安装 Elastic Stack 8.x。在其中的文章中,我们大多采用默认的证书来安装 Elasticsearch。在今天的文章中,我们用自己创…...

HADOOP--yarn ,, git
Yarn架构体系 主从架构 也是采用 master(Resource Manager)- slave (Node Manager)架构,Resource Manager 整个集群只有一个,一个可靠的节点。 1、 每个节点上可以负责该节点上的资源管理以及任务调度&am…...
IOS开发指南之UITableView控件使用
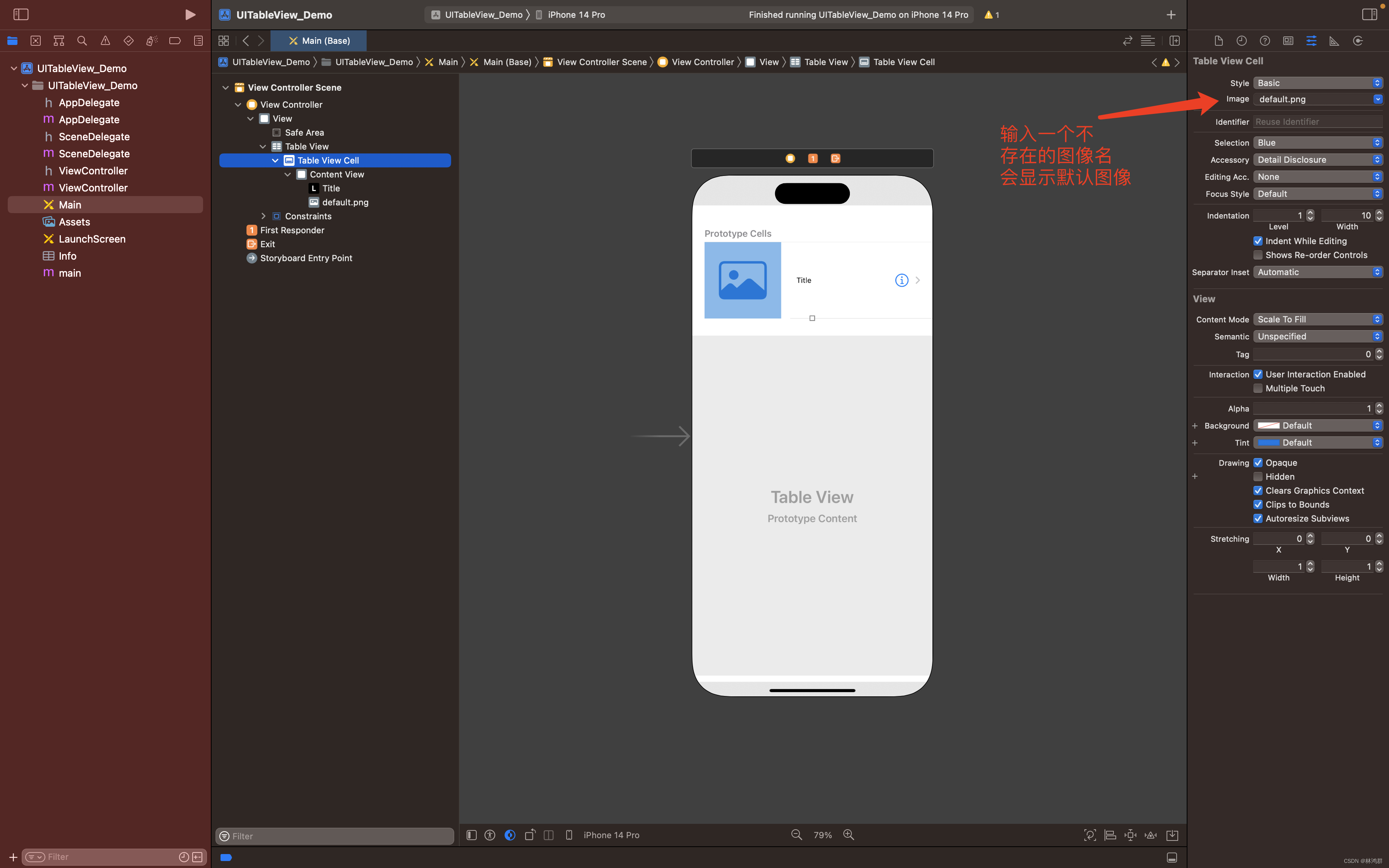
1.创建一个IOS单页应用 2.双击Main.storyboard然后拖放UITableView到视图中 3.添加TableViewCell 成功添加Table View Cell 4.修改Table View Cell属性 选中Table View Cell 在右边的Image栏输入default.png回车 到此布局设计完成,现在运行还是显示 空白,要在代码中做相关的实…...
C语言中的数据类型
目录 一、数据类型 1.基本类型 2.sizeof运算符 3.signed和unsigned 二、基本数据类型的取值范围 1.比特位 2.字节 3.符号位 4.补码 5.基本数据类型的取值范围 一、数据类型 1.基本类型 (1)整数类型 short intintlong intlong long int &…...
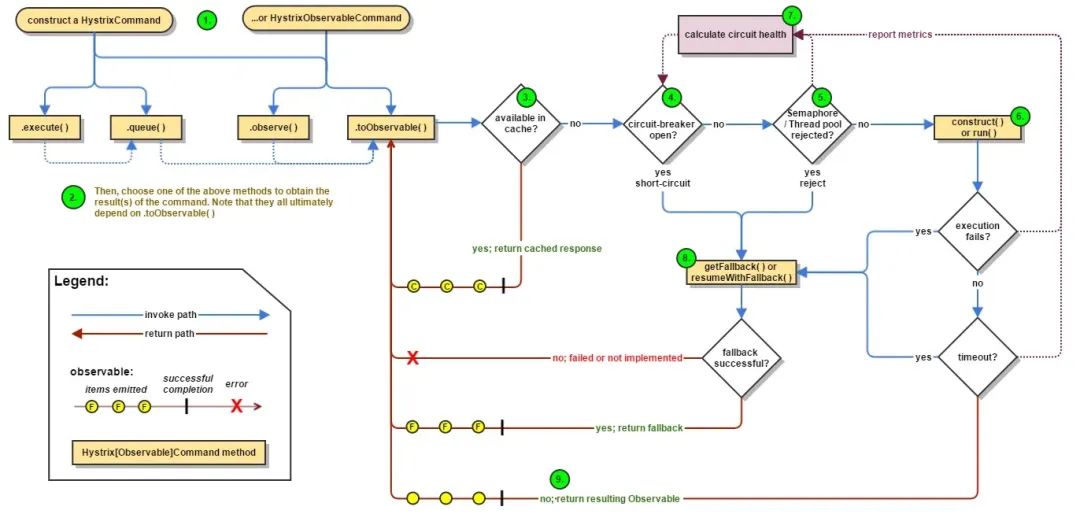
什么是微服务中的熔断器设计模式?
在本文中,我将解释什么是熔断器设计模式以及它解决了什么问题。 我们将仔细研究熔断器设计模式,并探讨如何使用Spring Cloud Netflix Hystrix在Java中实现它。到本文结束时,您将更好地了解如何使用熔断器设计模式提高微服务架构的弹性。 熔断…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
