使用apisix代理静态文件
前言
最近公司考虑用apisix作为公司网关并且部署到k8s上,我这边收到一个小任务:使用apisix代理静态文件
通过apisix官网了解到它构建于 NGINX + ngx_lua 的技术基础之上,所以按理应该和nginx代理静态资源是一样的。因为是通过docker容器部署的,需要考虑将静态资源路径挂载出来。
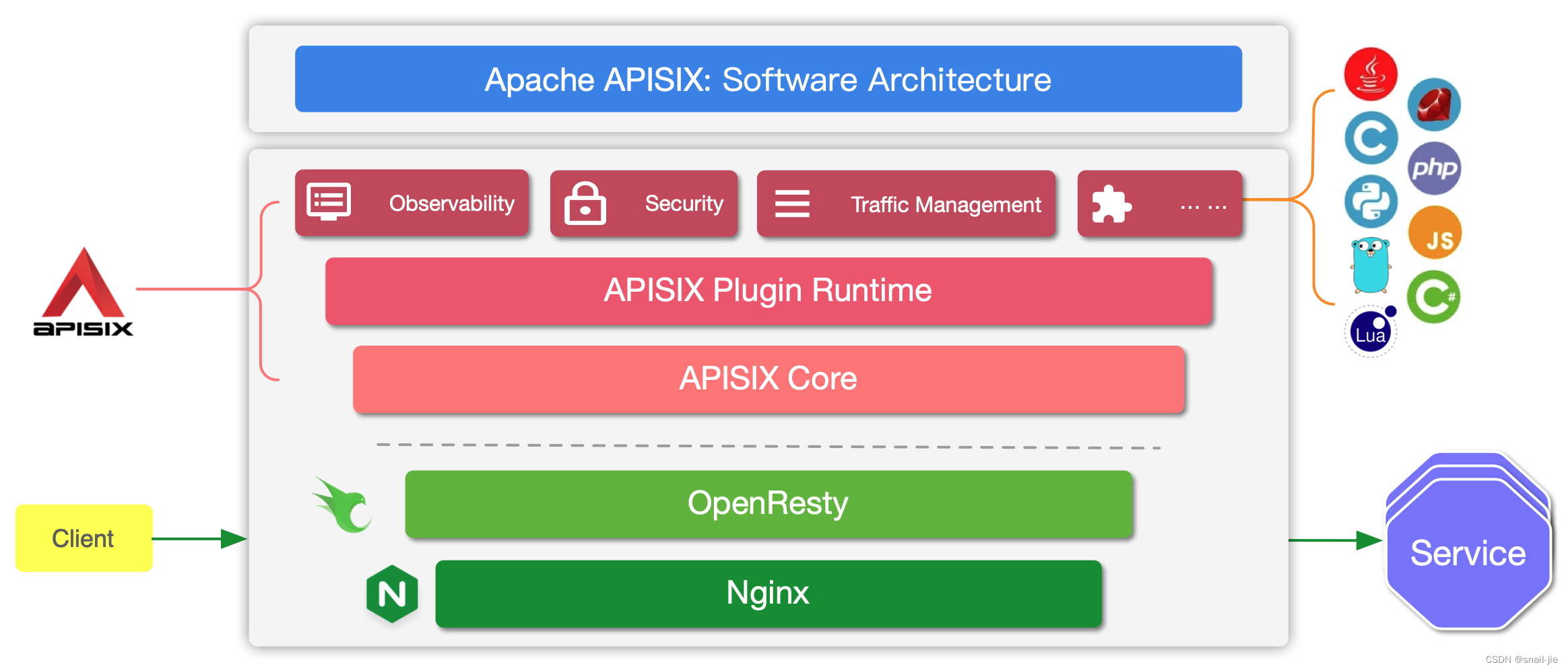
操作步骤
创建持久卷声明
- 通过kubesphere创建持久卷声明
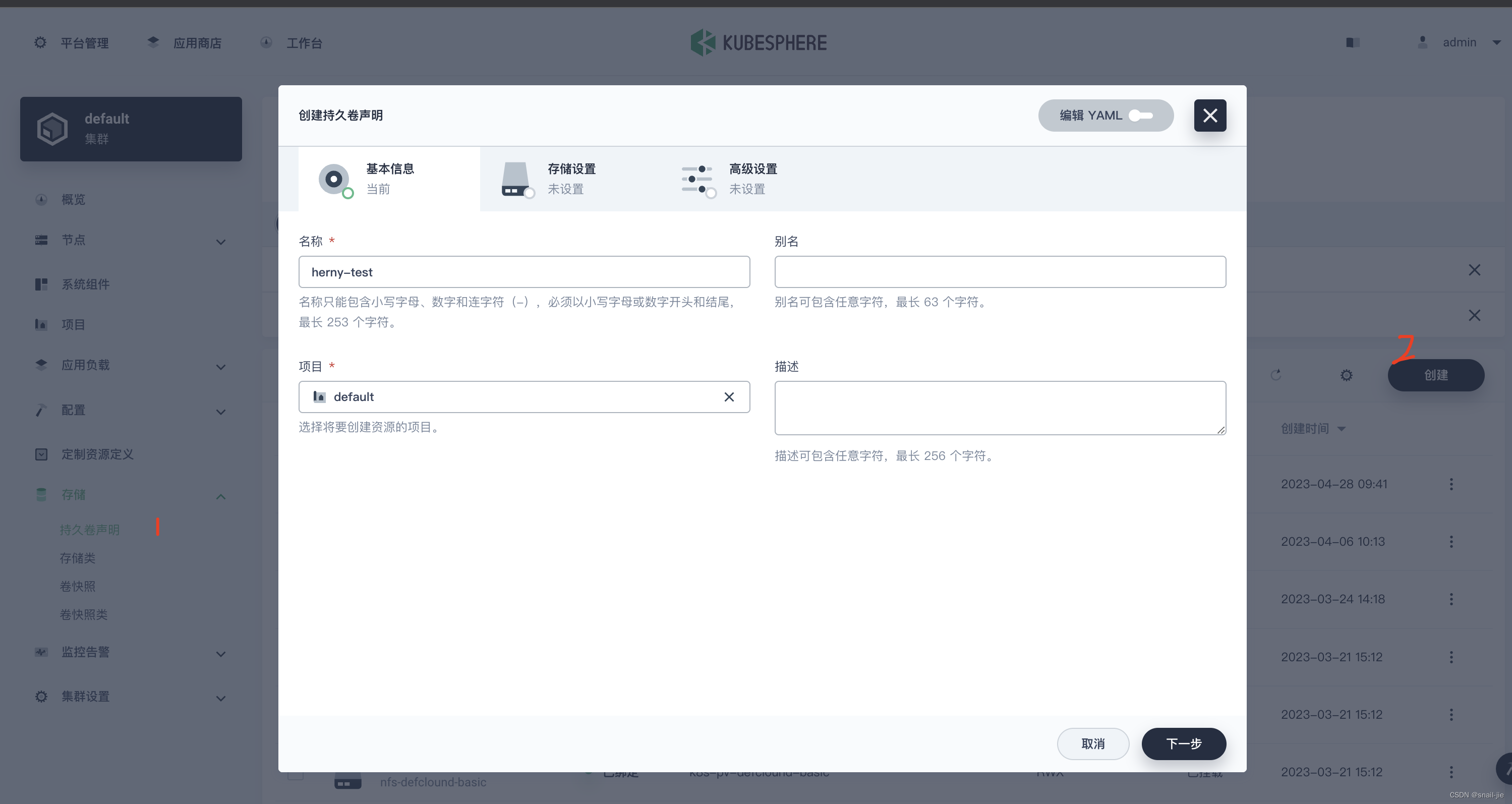
- 在存储设置中选择通过存储类创建,存储类选择local
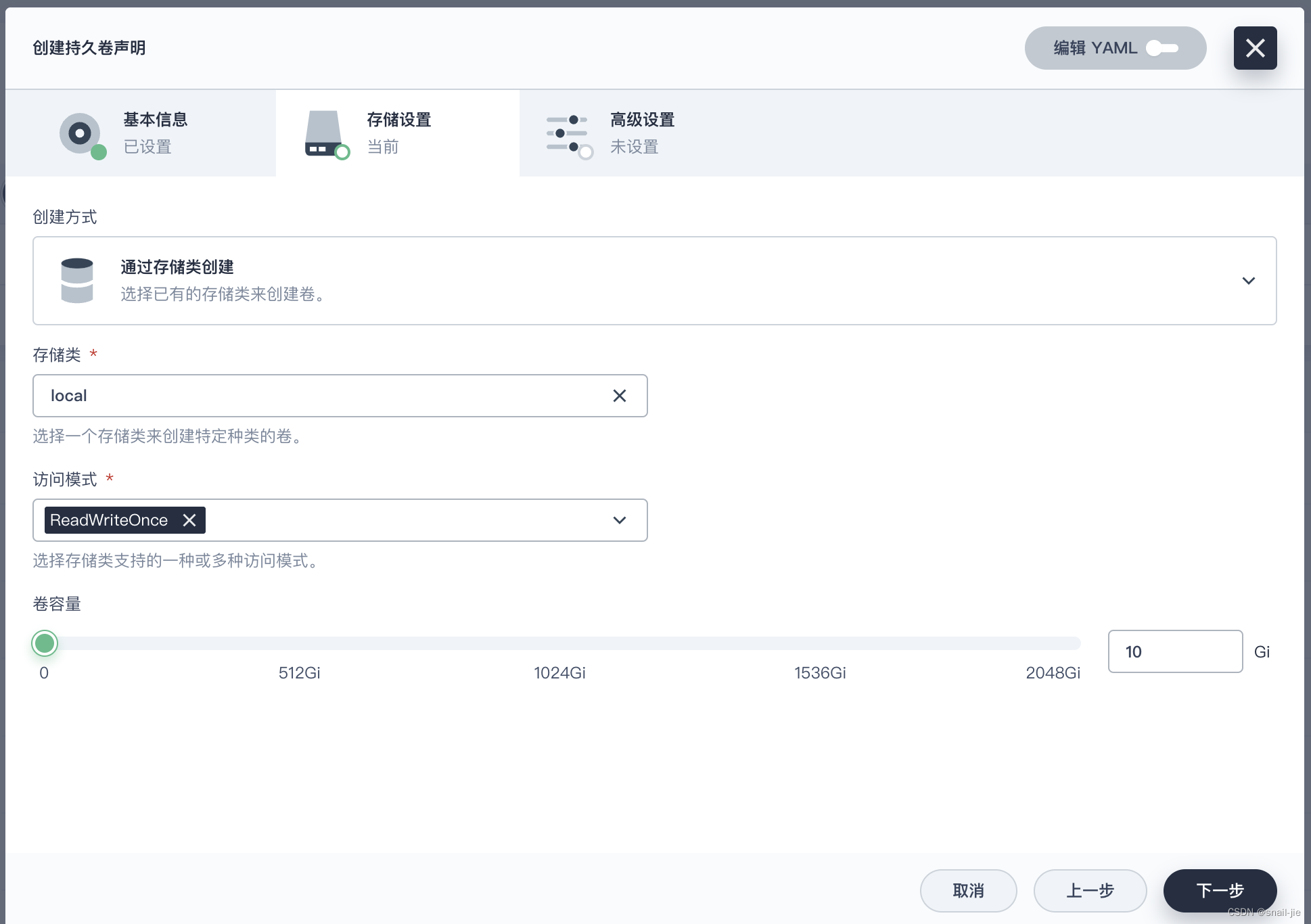
- 创建完后此时的状态为等待中,持久卷此时还未生成
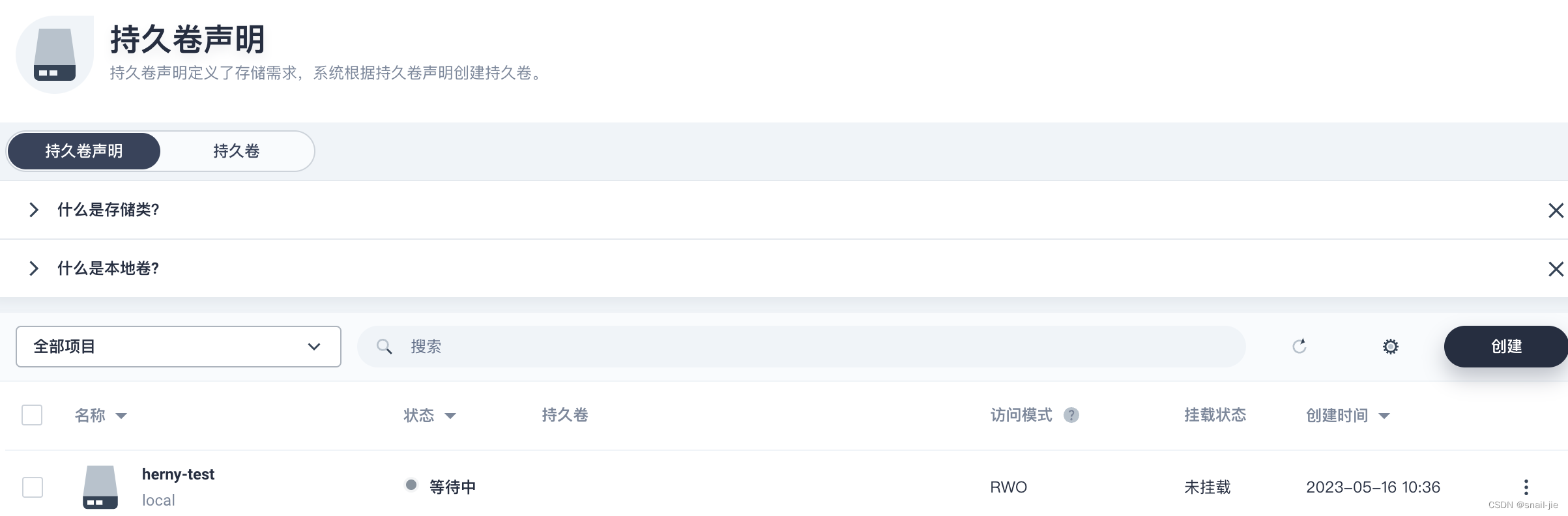
apisix负载挂载卷
- 编辑设置apisix负载
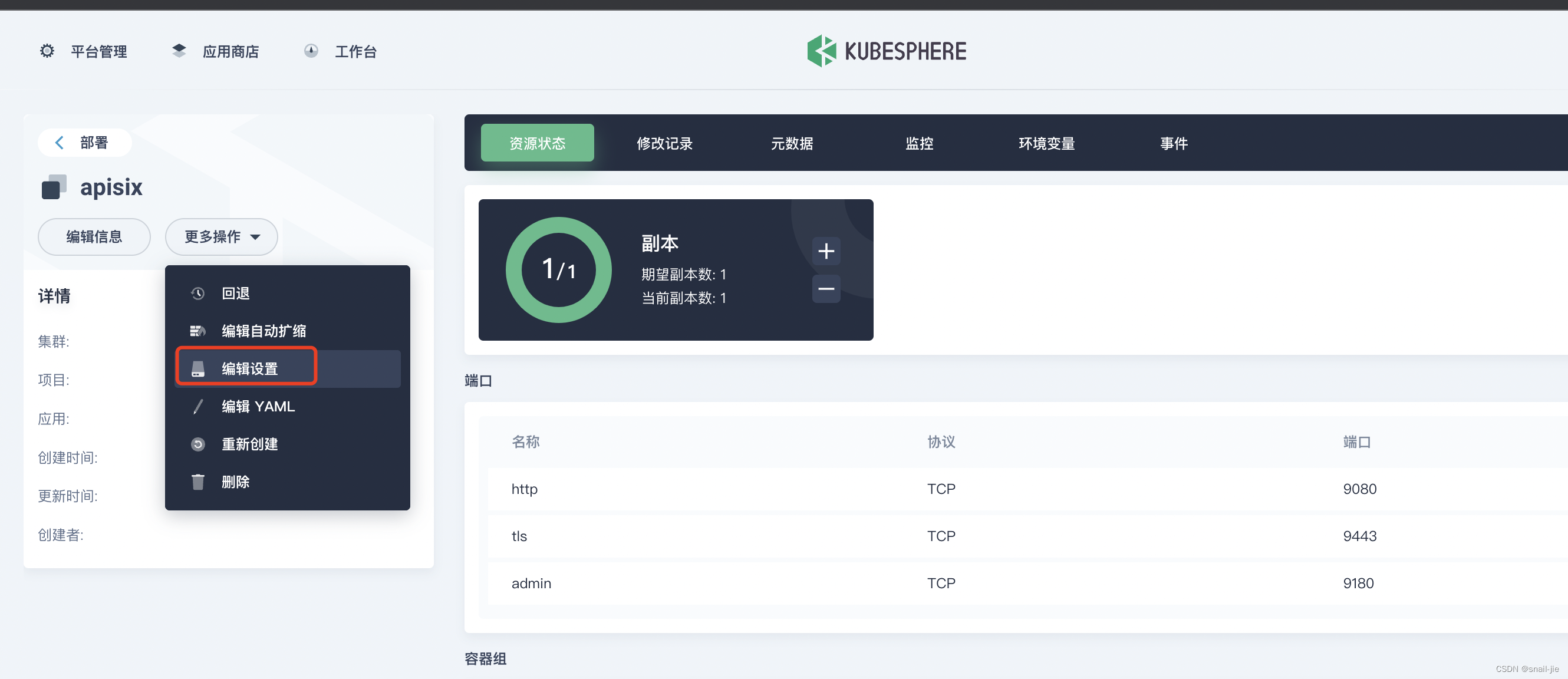
- 存储设置选择上面的持久卷声明,apisix挂载对应的容器目录(注意:这个挂载的容器路径与持久卷路径是一一对应关系)
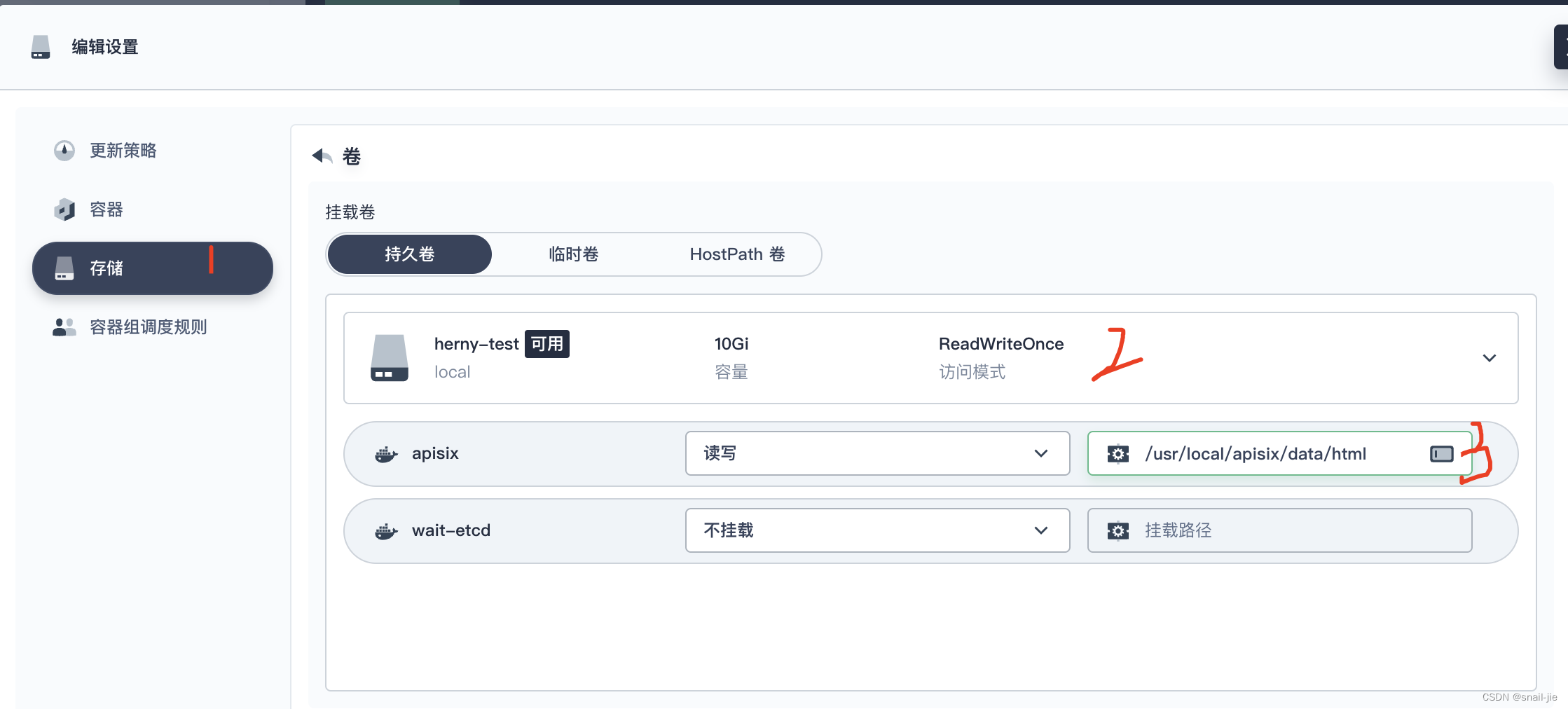
- 等待apisix重启成功后,切换存储->持久卷声明界面查看此时状态为已绑定并且生成了持久卷
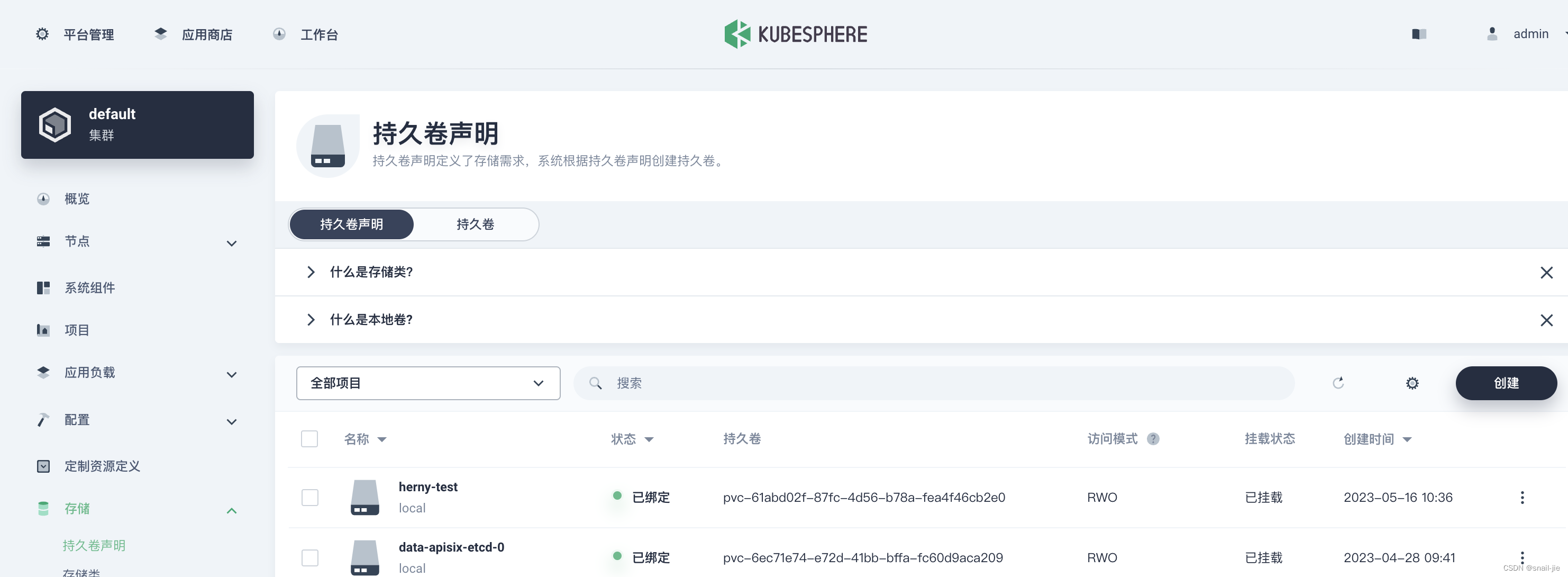
- 查看持久卷的路径
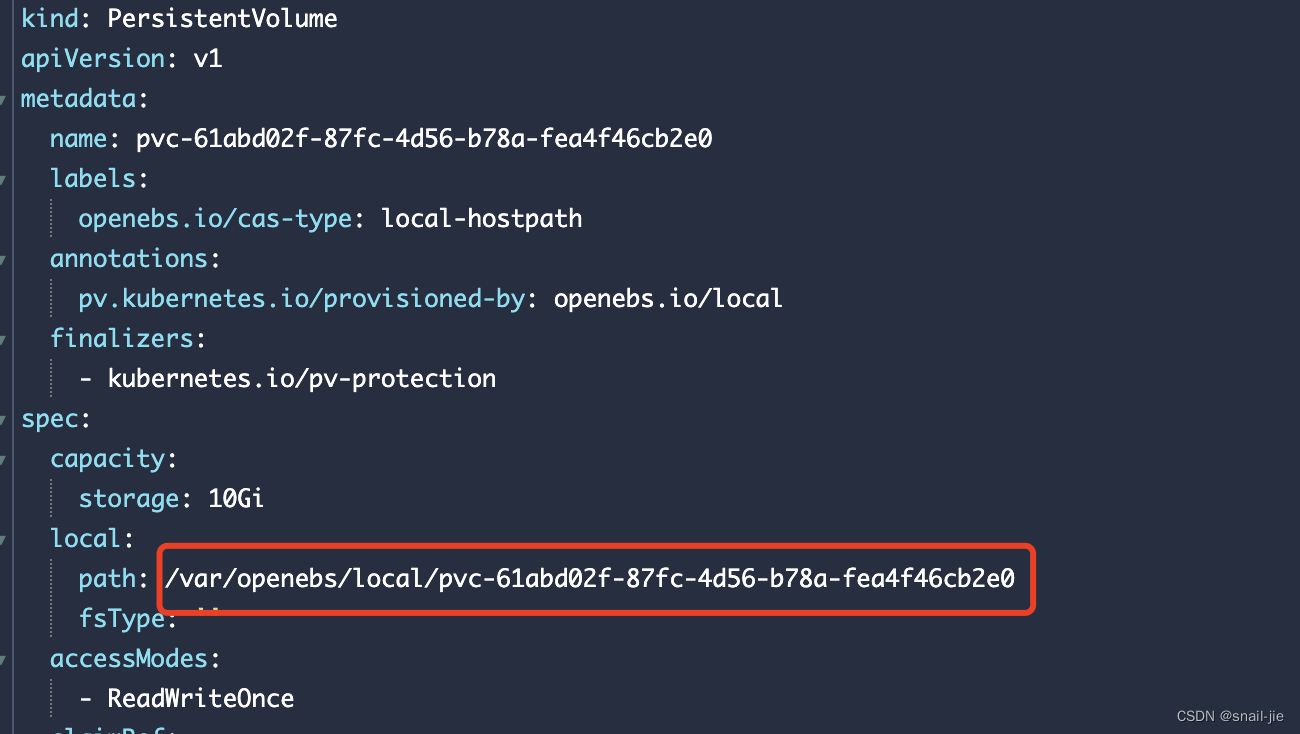
apisix设置静态资源路由
- 在config.yaml中添加自定义路由(apisix会根据config.yaml配置最终生成nginx.conf)
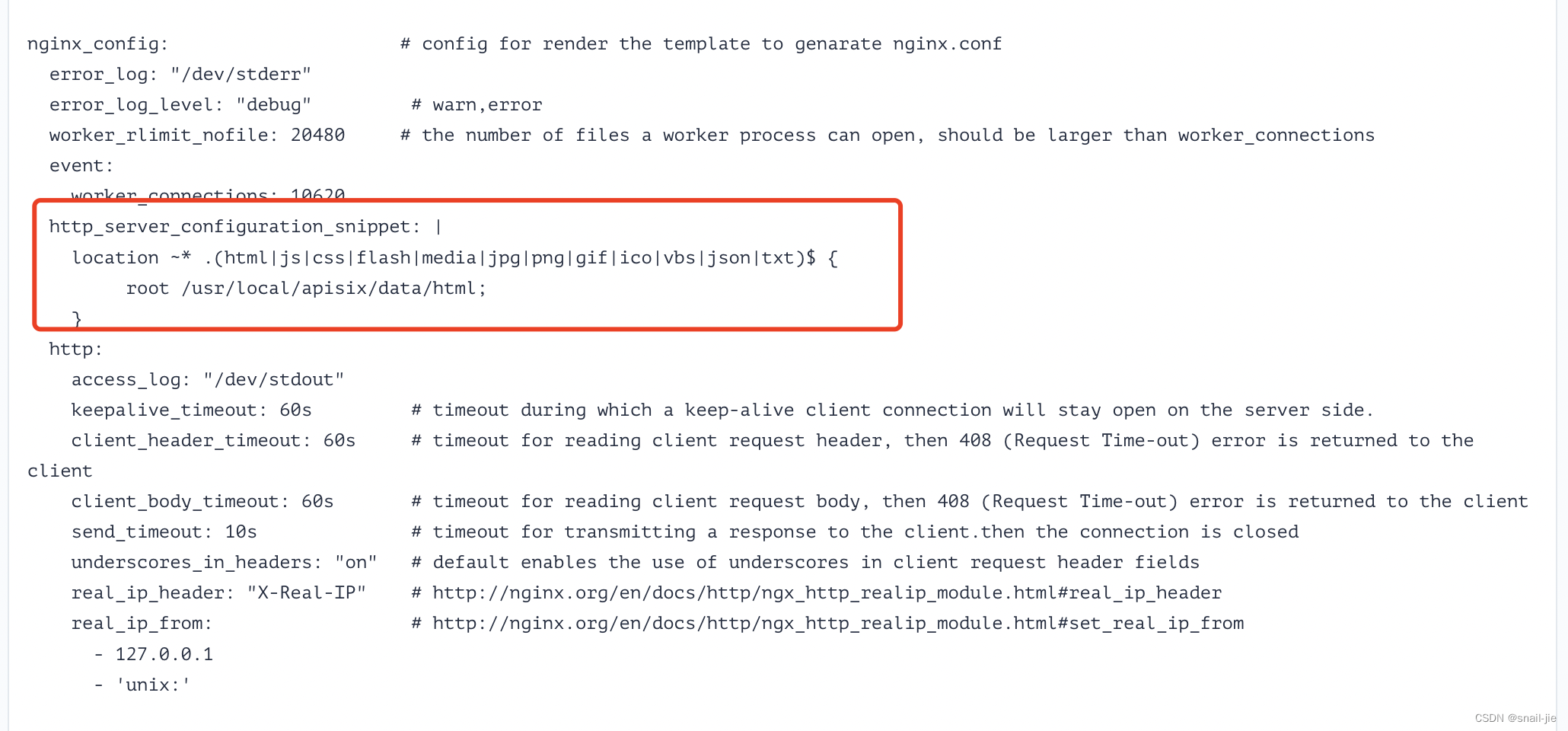
- 补充nginx相关语法知识
server {// 配置的路径+完整访问路径(完整的location配置路径+静态文件)// 响应http://localhost/about/example.html请求时,nginx将发送/data/www/about/example.html文件location / {root /data/www;}// 配置路径+静态文件(去除location中配置的路径)location /images/ {alias /data;} }
结果验证
- 在apisix负载挂载卷后会自动生成对应挂载目录

- 当持久卷被应用绑定后,在应用上的机器会生成对应持久卷目录

- 在持久卷路径中添加静态资源,容器挂载的目录会生成对应静态资源

- 通过apisix直接访问静态资源

相关文章:

使用apisix代理静态文件
前言 最近公司考虑用apisix作为公司网关并且部署到k8s上,我这边收到一个小任务:使用apisix代理静态文件 通过apisix官网了解到它构建于 NGINX ngx_lua 的技术基础之上,所以按理应该和nginx代理静态资源是一样的。因为是通过docker容器部署…...
)
[元带你学NVMe协议] NVMe1.4 多路径(Multipathing)
声明 主页:元存储的博客_CSDN博客 依公开知识及经验整理,如有误请留言。 个人辛苦整理,付费内容,禁止转载。 内容摘要 全文9100字, 主要内容 目录 前言 1 多路径(Multipathing)概念...

Elasticsearch:如何使用自定义的证书安装 Elastic Stack 8.x
在我之前的文章 “如何在 Linux,MacOS 及 Windows 上进行安装 Elasticsearch”,我详细描述了如何在各个平台中安装 Elastic Stack 8.x。在其中的文章中,我们大多采用默认的证书来安装 Elasticsearch。在今天的文章中,我们用自己创…...

HADOOP--yarn ,, git
Yarn架构体系 主从架构 也是采用 master(Resource Manager)- slave (Node Manager)架构,Resource Manager 整个集群只有一个,一个可靠的节点。 1、 每个节点上可以负责该节点上的资源管理以及任务调度&am…...
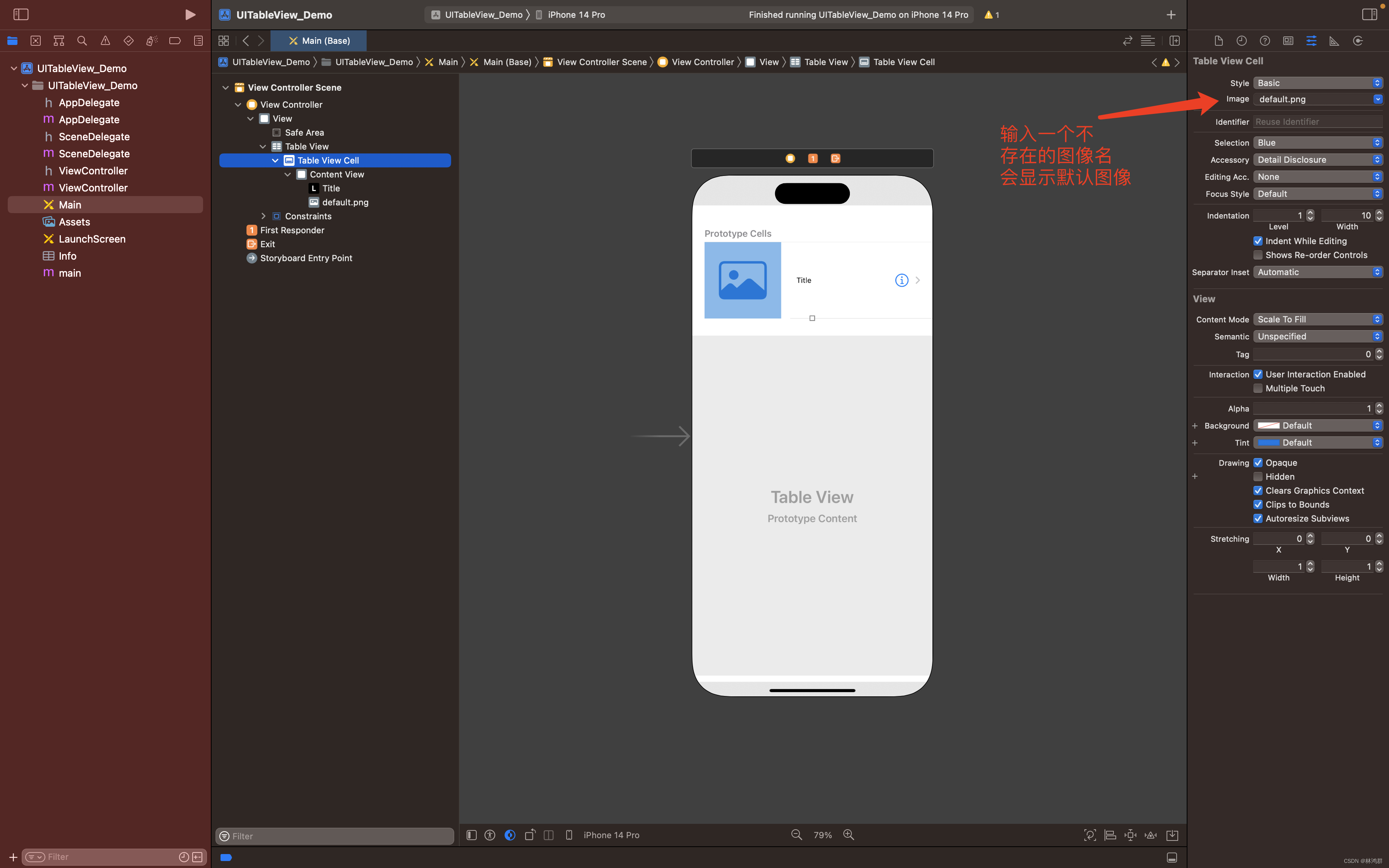
IOS开发指南之UITableView控件使用
1.创建一个IOS单页应用 2.双击Main.storyboard然后拖放UITableView到视图中 3.添加TableViewCell 成功添加Table View Cell 4.修改Table View Cell属性 选中Table View Cell 在右边的Image栏输入default.png回车 到此布局设计完成,现在运行还是显示 空白,要在代码中做相关的实…...
C语言中的数据类型
目录 一、数据类型 1.基本类型 2.sizeof运算符 3.signed和unsigned 二、基本数据类型的取值范围 1.比特位 2.字节 3.符号位 4.补码 5.基本数据类型的取值范围 一、数据类型 1.基本类型 (1)整数类型 short intintlong intlong long int &…...
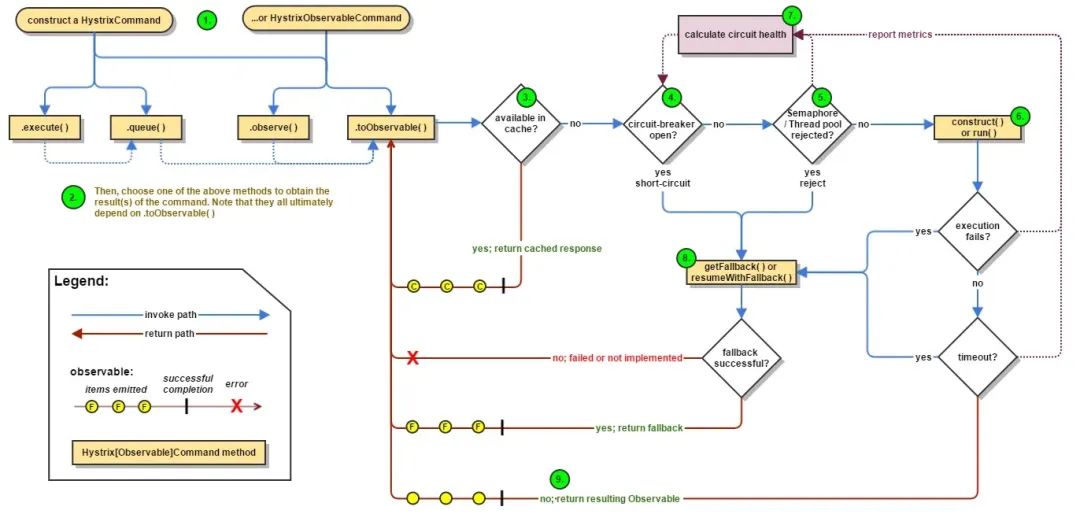
什么是微服务中的熔断器设计模式?
在本文中,我将解释什么是熔断器设计模式以及它解决了什么问题。 我们将仔细研究熔断器设计模式,并探讨如何使用Spring Cloud Netflix Hystrix在Java中实现它。到本文结束时,您将更好地了解如何使用熔断器设计模式提高微服务架构的弹性。 熔断…...

Ubuntu查看系统日志的几种方法
在 Ubuntu 22.10 中,你可以查看系统日志来排查错误。以下是几种查看日志的方法: 一、Journalctl 命令: 使用 journalctl 命令可以查看系统日志信息,包括引起闪退的错误信息。你可以运行以下命令来查看最新的系统日志:…...

【ubuntu】安装ZIP
【ubuntu】安装ZIP 输入如下命令安装zip $ sudo apt-get install zip 输出信息如下: Reading package lists... Done Building dependency tree Reading state information... Done The following additional packages will be installed: unzip The follo…...

DiffDock源码解析
DiffDock源码解析 数据预处理 数据输入方式 df pd.read_csv(args.protein_ligand_csv), 使用的是csv的方式输入, 格式: 不管受体还是配体, 输入可以是序列或者3维结构的文件 如果蛋白输入的是序列,需要计算蛋白的三维结构&am…...
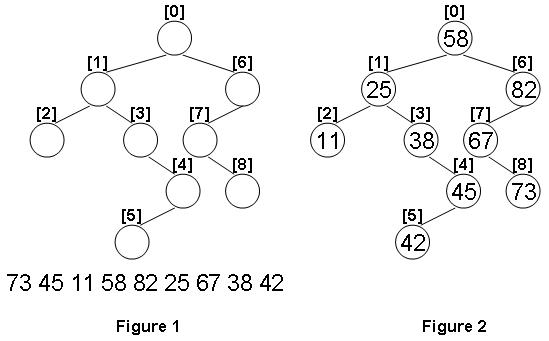
1099 Build A Binary Search Tree(超详细注解+38行代码)
分数 30 全屏浏览题目 作者 CHEN, Yue 单位 浙江大学 A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties: The left subtree of a node contains only nodes with keys less than the nodes key.The right subtree…...
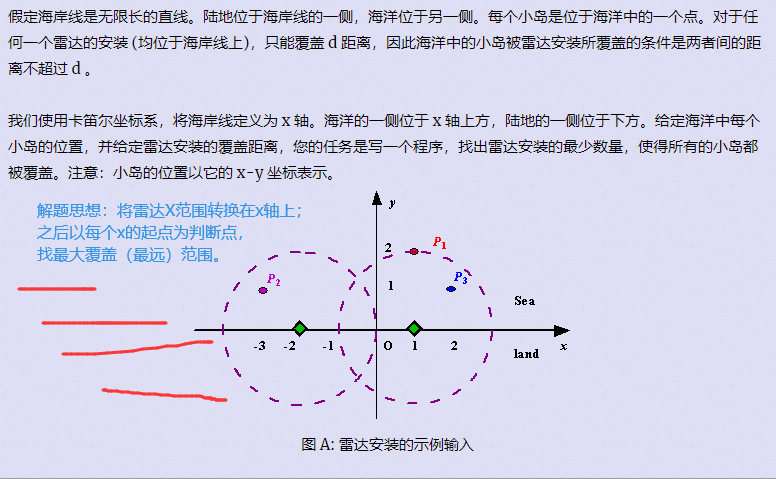
[刷题]贪心入门
文章目录 贪心区间问题区间选点区间合并区间覆盖 哈夫曼树(堆)合并果子 排序不等式排队打水 绝对值不等式货仓选址 推出来的不等式耍杂技的牛 以前的题 贪心 贪心:每一步行动总是按某种指标选取最优的操作来进行, 该指标只看眼前&…...
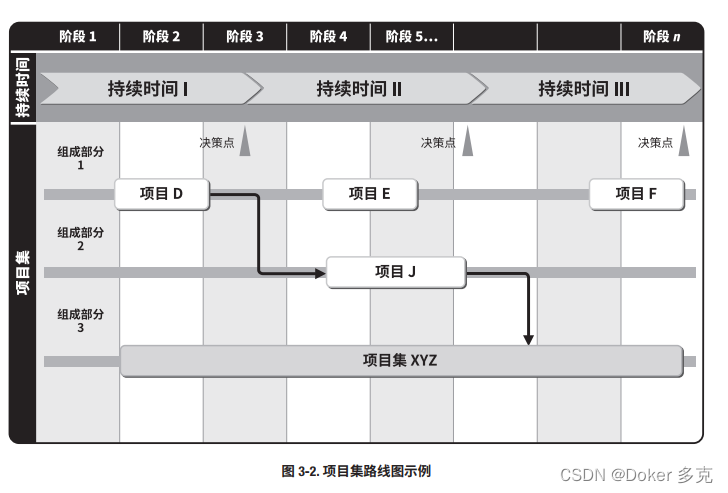
项目集战略一致性
项目集战略一致性是识别项目集输出和成果,以便与组织的目标和目的保持一致的绩效领域。 本章内容包括: 1 项目集商业论证 2 项目集章程 3 项目集路线图 4 环境评估 5 项目集风险管理战略 项目集应与组织战略保持一致,并促进组织效益的实现。为…...
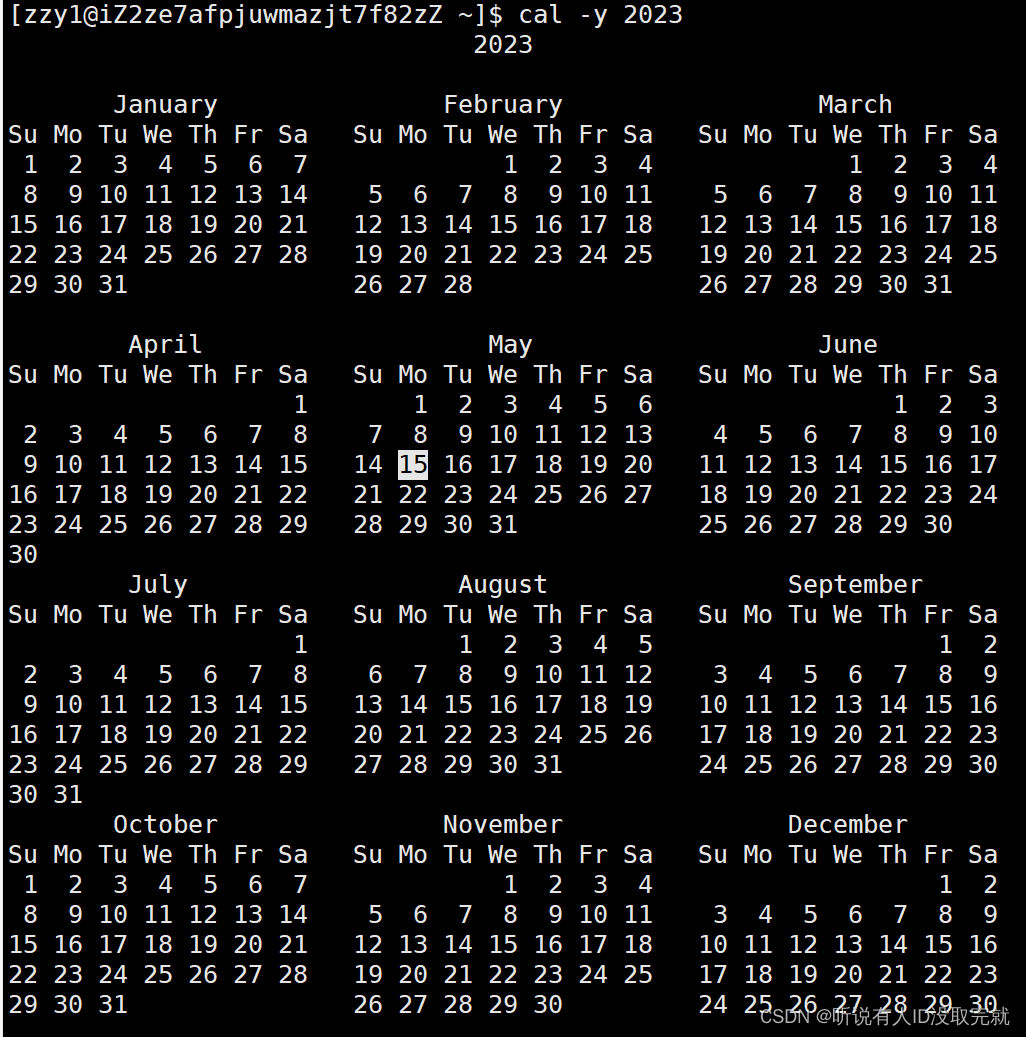
Linux学习 Day3
目录 1. 时间相关的指令 2. cal指令 3. find指令:(灰常重要) -name 4. grep指令 5. zip/unzip指令 6. tar指令(重要):打包/解包,不打开它,直接看内容 7. bc指令 8. uname –…...

前端开发推荐vscode安装什么插件?
前言 可以参考一下下面我推荐的插件,注意:插件的目的是用于提高开发的效率,节约开发的时间,像类似检查一些bug、拼写错误等这些可以使用插件快速的识别,避免在查找错误上浪费过多的时间,但切记不要过度依赖…...

如何打造完整的客户服务体系?
对于企业来说,提供优质的客户服务是保持竞争力和赢得市场份额的关键因素之一。一个高效、专业、人性化的客户服务体系,对于企业吸引和留住客户,提升品牌声誉,甚至增加销售额都有着不可忽视的作用。本文将从多个方面来阐述如何打造…...

裸奔时代,隐私何处寻?
随着互联网的普及,人工智能时代的大幕初启,数据作为人工智能的重要支撑,数据之争成为“兵家必争之地”,随之而来的就是,各种花式手段“收割”个人信息,用户隐私暴露程度越来越高,隐私保护早已成…...
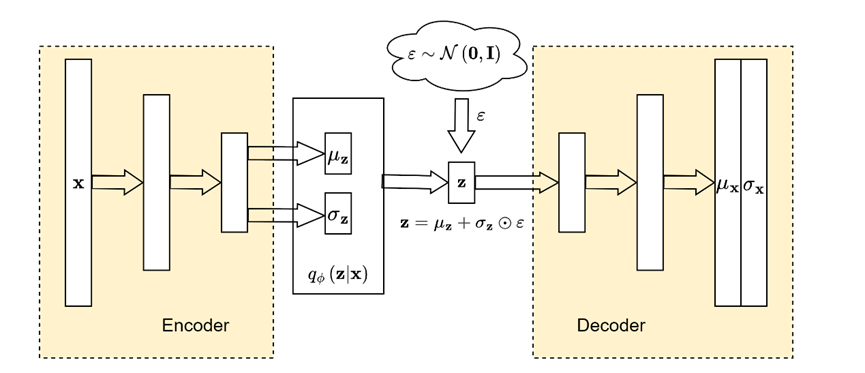
从期望最大化(EM)到变分自编码器(VAE)
本文主要记录了自己对变分自编码器论文的理解。 Kingma D P, Welling M. Auto-encoding variational bayes[J]. arXiv preprint arXiv:1312.6114, 2013. https://arxiv.org/abs/1312.6114 1 带有潜在变量的极大似然估计 假设我们有一个有限整数随机数发生器 z ∼ p θ ( z ) …...

【数学杂记】表达式中的 s.t. 是什么意思
今天写题的时候遇见了这个记号:s.t.,查了一下百度。 s.t.,全称 subject to,意思是“使得……满足”。 比如这个: 意思是存在 i i i,使得 i i i 满足 A i ≠ B i A_i\neq B_i AiBi. 运用这个记号…...

flink watermark介绍及watermark的窗口触发机制
Flink的三种时间 在谈watermark之前,首先需要了解flink的三种时间概念。在flink中,有三种时间戳概念:Event Time 、Processing Time 和 Ingestion Time。其中watermark只对Event Time类型的时间戳有用。这三种时间概念分别表示: …...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...
