当前位置： 首页 > news >正文

[离散数学] 函数

news 2026/2/8 18:56:00

文章目录

  • 函数
    • 判断函数的条件
    • 复合函数
      • 复合函数的性质
    • 逆函数

函数

在这里插入图片描述

判断函数的条件

dom F = A ⇔ \Leftrightarrow ⇔所有x 都有 F（x）与之对应
有唯一的与其对应 < x , y > ∈ f ∧ < y , z > ∈ f ⇒ y = z <x,y>\in f \land <y,z>\in f \Rightarrow y =z <x,y>∈f∧<y,z>∈f⇒y=z
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
|A| = m （基数） ,|B|=n (m,n 不全为0)
| B A B^A BA|= n m n^m nm

在这里插入图片描述
单射 ⇔ 入射 \Leftrightarrow 入射 ⇔入射 （一一对应）（ f ( x 1 ) = f ( x 2 ) ⇒ x 1 = x 2 f(x1)=f(x2) \Rightarrow x1=x2 f(x1)=f(x2)⇒x1=x2）
值域全包含—>满射 y ∈ B ⇒ ∃ x （ x ∈ A ∧ y = f ( x ) ） y\in B\Rightarrow \exists x（x\in A \land y = f(x)） y∈B⇒∃x（x∈A∧y=f(x)）
单射+满射=双射
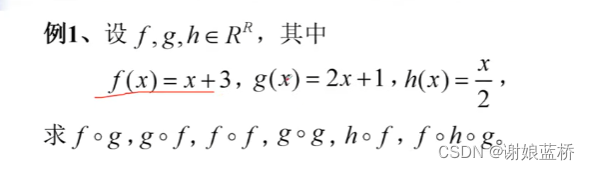
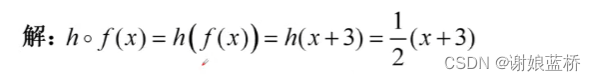
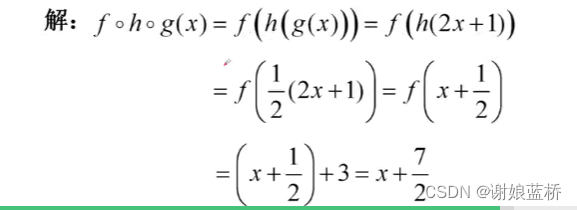
在这里插入图片描述
在这里插入图片描述
不是函数

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

复合函数

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

复合函数的性质

在这里插入图片描述
在这里插入图片描述

逆函数

函数不一定存在逆函数
如果函数双射，则存在逆函数
在这里插入图片描述在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

相关文章：

[离散数学] 函数

文章目录 函数判断函数的条件复合函数复合函数的性质 逆函数 函数 判断函数的条件 dom F A ⇔ \Leftrightarrow ⇔所有x 都有 F&#xff08;x&#xff09;与之对应 有唯一的与其对应 < x , y > ∈ f ∧ < y , z > ∈ f ⇒ y z <x,y>\in f \land <y,z…...

编程日记 2023/5/17 0:59:51

好家伙，又一份牛逼笔记面世了...

最近网传的一些裁员的消息&#xff0c;搞的人心惶惶。已经拿到大厂offer的码友来问我&#xff1a;大厂还能去&#xff0c;去了会不会被裁。 还在学习的网友来问我&#xff1a;现在还要冲互联网么&#xff1f; 我是认为大家不用恐慌吧&#xff0c;该看啥看啥&#xff0c;该学啥…...

编程日记 2023/5/17 0:54:50

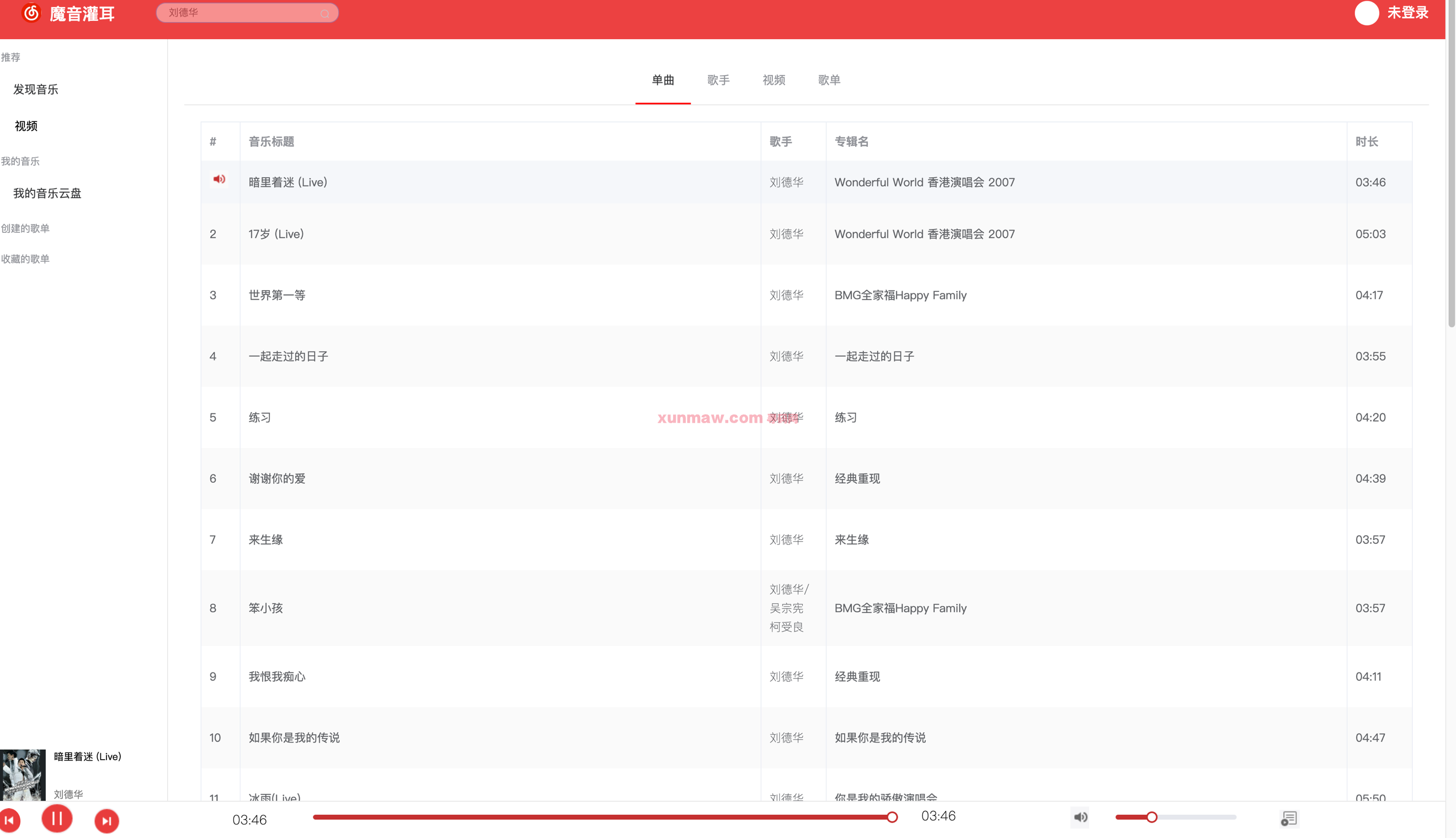
基于nodejs+vue3 的高仿网易云音乐

大家好&#xff0c;我是小寻&#xff0c;欢迎大家关注我的公众号&#xff1a;工具优选&#xff0c;加入前端、java群聊哦&#xff01; 今天给大家分享一个超高水准的项目&#xff1a;基于nodejsvue3研发的高仿网易云音乐&#xff0c;项目内容出自寻码网&#xff01; 技术栈&a…...

编程日记 2023/6/1 8:18:13

MySQL数据库用户管理以及数据库用户授权

一、数据库用户管理 1、新建用户 CREATE USER 用户名来源地址 [IDENTIFIED BY [PASSWORD] 密码]; ---------------------------------------------------------------------------------------------------------- 用户名&#xff1a;指定将创建的用户名 来源地址&#xff1a…...

编程日记 2023/5/17 0:44:48

全面分析生物技术的优缺点以及应用场景

一、 引言 生物识别技术具有不可撤销性、高度便利性和较低错误率等优势&#xff0c;在安全领域中也备受瞩目。然而&#xff0c;对于生物识别技术在应对安全挑战方面的可靠性和有效性&#xff0c;但争议并未被完全解决 二、生物识别技术的介绍 所谓生物识别技术就是&#xff0c;…...

编程日记 2023/5/17 0:39:47

OpenAI是什么？

OpenAI是一家人工智能技术公司&#xff0c;成立于2015年&#xff0c;总部位于美国旧金山。它的创始人包括埃隆马斯克等多名知名人士&#xff0c;公司的目标是推进人工智能技术的发展&#xff0c;同时确保人工智能的发展不会对人类造成负面影响。 OpenAI在研究和开发各种人工智能…...

编程日记 2023/5/17 0:34:46

量子计算——新兴领域的前沿技术

随着人类社会文明的不断进步&#xff0c;计算技术也在不断发展。传统计算机在过去的几十年中快速发展&#xff0c;计算速度、存储能力等方面发生了天翻地覆的变化。但随着大数据、人工智能、区块链等新兴领域的迅速崛起&#xff0c;传统计算机的发展似乎面临了瓶颈。在这样的背…...

编程日记 2023/5/17 0:29:45

.Net平台下OpenGL绘制图形（1）(VS2019,Winform,C#)

1、介绍 OpenGL&#xff08;英语&#xff1a;Open Graphics Library&#xff0c;译名&#xff1a;开放图形库或者“开放式图形库”&#xff09;是用于渲染2D、3D矢量图形的跨语言、跨平台的应用程序编程接口&#xff08;API&#xff09;。这个接口由近350个不同的函数调用组成…...

编程日记 2023/5/17 0:24:44

Casso的创作纪念日

机缘 注册CSDN的时候才刚上大学&#xff0c;到现在使用CSDN已经四年了&#xff0c;距发布第一篇文章却只刚过去一百多天&#xff0c;刚看到这个提醒消息的时候只感慨时间过得真快&#xff0c;自己也在慢慢成长着&#xff0c;当初刚开始学习的时候&#xff0c;查资料用得最多的就…...

编程日记 2023/5/17 0:19:43

Bernhard‘s Talk on Towards Causal NLP 笔记

因果学习系列笔记 这是我的 GitHub 因果学习笔记仓库 https://github.com/xin007-kong/ryCausalLearning&#xff0c;欢迎 star&#x1f929; 讲者是 Bernhard Schlkopf talk 链接&#xff1a;(41) Bernhard Schoelkopf | Towards Causal NLP | KeynoteEMNLP 2021 Causal Infer…...

编程日记 2023/5/31 6:40:54

ES6模块化规范

在没有ES6模块化规范前&#xff0c;有像AMD、CMD这样的浏览器模块化规范&#xff0c;还有像CommonJS这样的服务端模块化规范。 2015年&#xff0c;JS终于推出了官方的模块化规范&#xff0c;为了统一各种规范&#xff0c;我们简称ES6 模块化。 ES6目前作为JS的内置模块化系统&a…...

编程日记 2023/5/17 0:09:42

红黑树下岗，内核新数据结构上场：maple tree！

在外界看来&#xff0c;Linux 内核的内部似乎变化很少&#xff0c;尤其是像内存管理子系统&#xff08;memory-management subsystem&#xff09;这样的子系统。然而&#xff0c;开发人员时常需要更换内部接口来解决某些长期存在的问题。比如&#xff0c;其中一个问题就是用来保…...

编程日记 2023/5/17 0:04:41

Angular开发之——Angular打包部署项目(04)

一 概述 ng build 构建应用lite-server介绍及安装lite-server部署应用IIS管理器部署应用 二 ng build 构建应用 2.1 执行如下指令构建应用 ng build2.2 构建完成后&#xff0c;会创建一个 dist 文件夹 2.3 直接打开index.html会出错(需要借助于服务器部署) 三 lite-server介…...

编程日记 2023/5/16 23:59:40

深度优先搜索算法思想，题型总结与题目清单（不断更新）

深度优先搜索 深度优先搜索&#xff08;Depth-First Search&#xff0c;简称DFS&#xff09;是一种用于遍历或搜索树或图的算法。这个名称直接来自于这个算法的操作方式&#xff1a;它沿着某一路径深入遍历直到无法继续&#xff0c;然后再回溯进行下一条路径的遍历。 DFS的主要…...

编程日记 2023/5/16 23:54:34

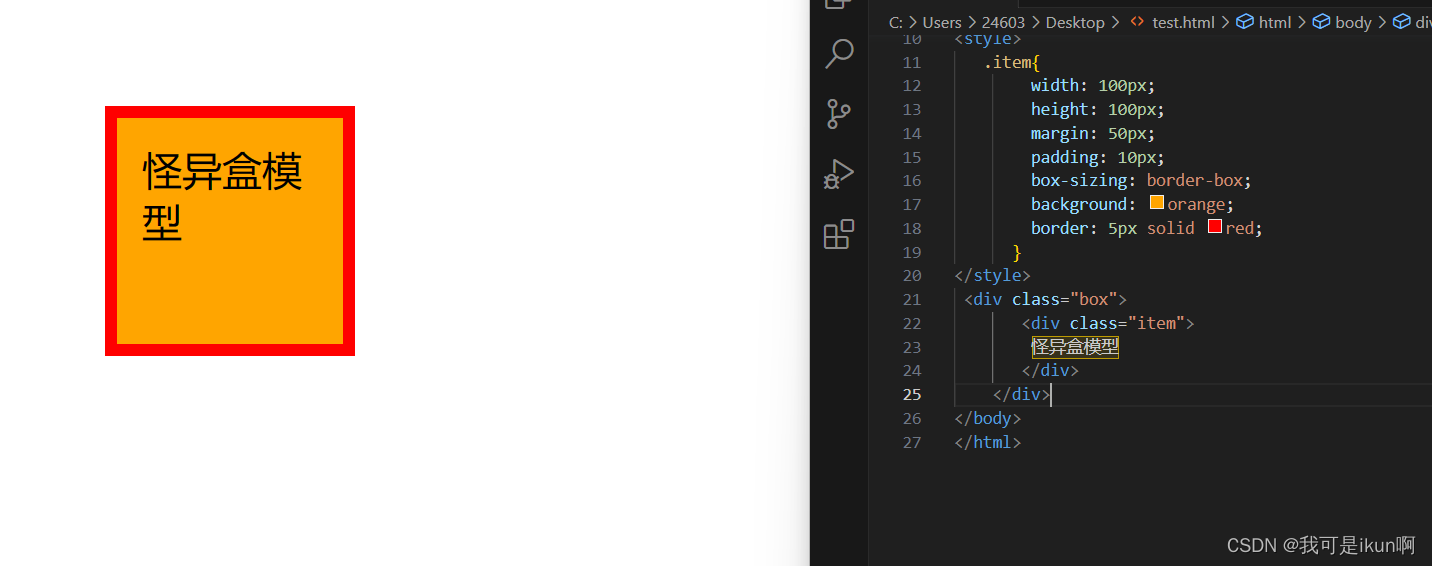
网页三剑客之 CSS

css 在这里不会介绍太多&#xff0c;我们主要重点介绍两个&#xff1a;选择器和盒子模型就够用了。这里看个乐就好了&#xff0c;没有那么多重点&#xff0c;只是简单的认识一下下CSS。 CSS 是什么 CSS 是层叠样式表 (Cascading Style Sheets)的缩写它存在的意义就是&#xf…...

编程日记 2023/5/16 23:49:33

Maven（1）--- Maven入门指南

当然&#xff0c;我可以为你提供Maven的详细介绍&#xff0c;并按照6篇文章的方式进行详细展开。下面是第一篇的内容&#xff0c;采用Markdown格式输出&#xff1a; Maven入门指南 什么是Maven&#xff1f; Maven是一个强大的项目管理工具&#xff0c;被广泛应用于Java项目开…...

编程日记 2023/5/16 23:44:32

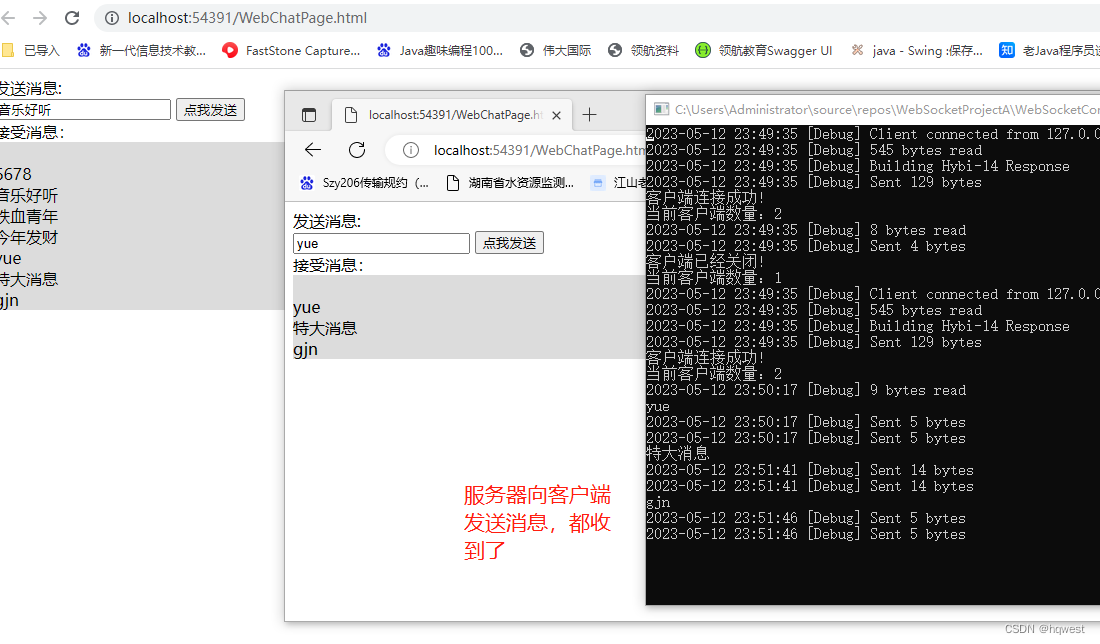
C# 实现 Websocket通讯聊天 (管用、超好使，点个赞)

1、背景 WebSocket出现之前&#xff0c;Web端为了实现即时通讯&#xff0c;所用的技术都是Ajax轮询(polling)。轮询是在特定的的时间间隔&#xff08;如每1秒&#xff09;&#xff0c;由浏览器对服务器发出HTTP request&#xff0c;然后由服务器返回最新的数据给客服端的浏览器…...

编程日记 2023/5/16 23:39:31

知识点回顾（一）

1.final,finally ,finalize final?修饰符&#xff08;关键字&#xff09;如果一个类被声明为final&#xff0c;意味着它不能再派生出新的子类&#xff0c;不能作为父类被继承。因此一个类不能既被声明为 abstract的&#xff0c;又被声明为final的。将变量或方法声明为final&…...

编程日记 2023/5/16 23:34:30

verflow属性的常用值详解

什么是overflow 在CSS中&#xff0c;overflow是“溢出”的意思&#xff0c;该属性规定当内容溢出元素框时发生的事情&#xff0c;设置内容是否会被修剪&#xff0c;溢出部分是否会被隐藏&#xff1b;例如当属性值设置为“visible”则内容不会被修剪&#xff0c;为“hidden”则内…...

编程日记 2023/5/16 23:29:29

算法怎么算：贪心算法

总有人在小白面前说&#xff1a;我是搞算法的&#xff0c;不是码农。又或者在想要进阶的时候&#xff0c;有人问你&#xff1a;你懂算法吗&#xff1f; 所有&#xff0c;算法到底是什么&#xff1f; 从目的性来说&#xff1a;它是计算方法&#xff0c;用来达到自己目的的方式…...

编程日记 2023/5/16 23:24:28

MySQL中【正则表达式】用法

MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现&#xff08;两者等价&#xff09;&#xff0c;用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例&#xff1a; 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

编程新知 2025/11/21 22:02:37

如何在网页里填写 PDF 表格？

有时候&#xff0c;你可能希望用户能在你的网站上填写 PDF 表单。然而&#xff0c;这件事并不简单&#xff0c;因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件&#xff0c;但原生并不支持编辑或填写它们。更糟的是&#xff0c;如果你想收集表单数据&#xff…...

编程新知 2026/2/6 22:20:51

docker 部署发现spring.profiles.active 问题

报错&#xff1a; org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

编程新知 2025/9/20 12:14:18

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习

禁止商业或二改转载&#xff0c;仅供自学使用&#xff0c;侵权必究&#xff0c;如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

编程新知 2026/2/6 11:41:39

React---day11

14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store&#xff1a; 我们在使用异步的时候理应是要使用中间件的&#xff0c;但是configureStore 已经自动集成了 redux-thunk&#xff0c;注意action里面要返回函数 import { configureS…...

编程新知 2026/1/19 2:13:24

【JavaSE】多线程基础学习笔记

多线程基础 -线程相关概念 程序&#xff08;Program&#xff09; 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序&#xff0c;比如我们使用QQ&#xff0c;就启动了一个进程&#xff0c;操作系统就会为该进程分配内存…...

编程新知 2025/9/12 0:57:34

Razor编程中@Html的方法使用大全

文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

编程新知 2026/1/28 4:50:33

R 语言科研绘图第 55 期 --- 网络图-聚类

在发表科研论文的过程中&#xff0c;科研绘图是必不可少的&#xff0c;一张好看的图形会是文章很大的加分项。 为了便于使用&#xff0c;本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中&#xff0c;获取方式&#xff1a; R 语言科研绘图模板 --- sciRplothttps://mp.…...

编程新知 2026/1/30 2:34:31

前端中slice和splic的区别

1. slice slice 用于从数组中提取一部分元素&#xff0c;返回一个新的数组。 特点&#xff1a; 不修改原数组&#xff1a;slice 不会改变原数组&#xff0c;而是返回一个新的数组。提取数组的部分&#xff1a;slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

编程新知 2025/11/27 20:15:13

【C++】纯虚函数类外可以写实现吗？

1. 答案 先说答案&#xff0c;可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

编程新知 2026/2/7 17:44:12