你知道营销人为什么要讲洞察吗?
用户洞察,是制定品牌和产品战略的基础,基于深刻的用户洞察,才能谈价值发现,目标规划,产品设计,全方位运营等。
可以这么说,没有洞察就没有营销,因为你的营销策略不能凭空想象,没有用户洞察,你的策略就是空中楼阁。
一般来说,营销人说的洞察,是指对目标消费群体的深入了解和分析,从中发现潜在的需求、问题、行为模式等等,并形成有效的营销策略或产品创新的启示。
洞察通常不是表面上简单的数据分析,而需要通过深入访谈、用户体验研究、调查问卷等方式获取更为全面和真实的消费者反馈和态度。
洞察是营销策略成功的关键之一,能够帮助企业更好地理解消费者的需求和行为,从而提高产品市场的竞争力。
当谈到营销洞察时,我们可以以可口可乐的市场营销成败为例子,这样更容易理解。
可口可乐曾于1985年在美国推出一款新产品-新可乐(New Coke),试图取代自己原有的可口可乐(Coca-Cola Classic),却在上市数月后引起市场惨败,并遭到广泛的抨击和嘲笑。
这一事件的背后,很大程度上是因为可口可乐在推出新可乐之前未能充分了解当时消费者的需求和情感绑定。
可口可乐在推出新可乐之前,拥有着至今仍被认为是市场营销经典案例之一的“Pepsi Challenge”(百事可乐挑战赛)活动。
这一活动旨在放大百事可乐在口感测试和市场占有率方面的优势,并对可口可乐的市场地位构成直接挑战。
作为回应,可口可乐开始走访全美各地的消费者,以了解他们想喝什么样的可乐。
然而,当新可乐上市后,却发现消费者的反应与预期的完全不同。
许多人暴跳如雷,认为可口可乐公司的产品变革是在毁掉一种吉祥物、一种信仰。
由此,可口可乐迅速意识到其营销计划缺乏重要的“营销洞察”,即了解消费者比数据分析更深入、更真实的需求和情感反馈。
针对此情况,可口可乐很快终止了新可乐,重新推出了可口可乐经典配方,并将其市场定位为“传统、美味和带有怀旧感的饮品”,以回应消费者文化情感观念的需求。
这一行动在短时间内迅速赢得了市场的支持和市场份额的提高,变为一段著名的营销史上的成功案例。
以上案例表明,洞察是营销成功的关键之一。
企业对于消费者的深入了解,不仅能够更好地针对其需求而创造新产品,也能直接带来更大的品牌连贯性和市场竞争优势。
……
相关文章:

你知道营销人为什么要讲洞察吗?
用户洞察,是制定品牌和产品战略的基础,基于深刻的用户洞察,才能谈价值发现,目标规划,产品设计,全方位运营等。 可以这么说,没有洞察就没有营销,因为你的营销策略不能凭空想象&#…...
Neovim-配置教程
环境:Ubuntu 20.04 宿主机:windows (windows terminal)WSL2 NVIM:v0.10.0-dev 配置Neovim 需要保证流畅的github环境(以便于快速拉取插件),可以使用代理或是配置Github SSH key 本文…...
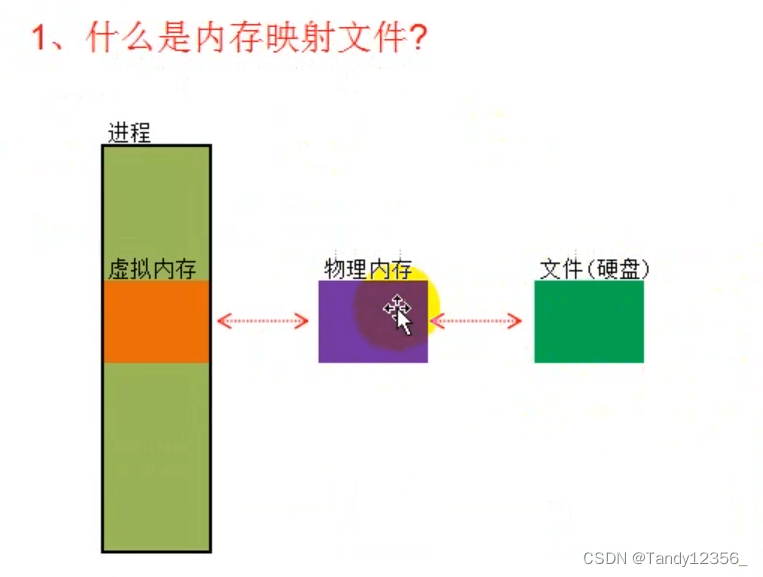
Windows管理内存的3种方式——堆、虚拟内存、共享内存
一、操作系统管理内存概述 在 Windows 操作系统中,每个进程都被分配了 4GB 的虚拟地址空间,这被称为进程的虚拟地址空间。虚拟地址空间提供了一个抽象的地址空间,使得每个进程都可以认为它拥有自己的独立内存空间。这个虚拟地址空间被分为两…...

PCM/FM解调原理与Matlab算法仿真
调制的作用是将调制信息的频谱从低频搬移到高频,以适合信道传输。关于调制的原理,在上一节中已经讲过了。在这一节中,主要讲解FM的解调原理。与调制相对应的是在接收端需要解调过程将调制信息复原,所以解调是影响通信系统性能的重要技术。 解调方法按照是否需要载波恢复的…...

我的『1024』创作纪念日
目录 ◐机缘 ◑收获 ◐日常 ◑成就 ◐憧憬 记得,2020年07月22日我撰写了第1篇技术博客:《遗传算法实例解析》在这平凡的一天,我赋予了它不平凡的意义也许是立志成为一名专业T作者、也许是记录一段刚实践的经验但在那一刻,我已…...
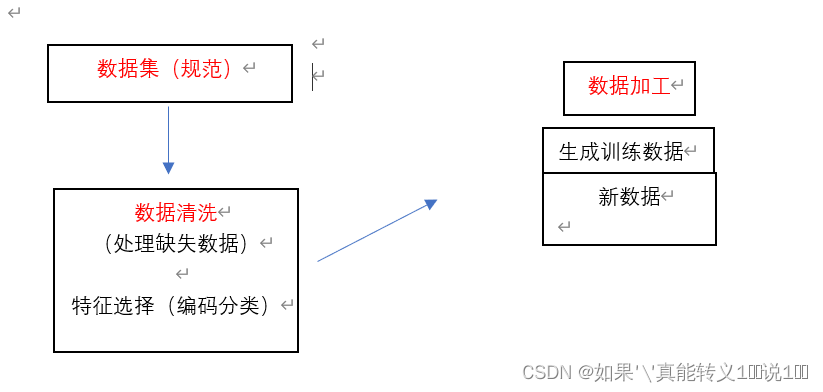
Python ---> 衍生的数据技术
我的个人博客主页:如果’真能转义1️⃣说1️⃣的博客主页 关于Python基本语法学习---->可以参考我的这篇博客:《我在VScode学Python》 随着人工智能技术的发展,挖掘和分析商业运用大数据已经成为一种推动应用, 推动社会发展起着…...

【27】linux进阶——rpm软件包的管理
大家好,这里是天亮之前ict,本人网络工程大三在读小学生,拥有锐捷的ie和红帽的ce认证。每天更新一个linux进阶的小知识,希望能提高自己的技术的同时,也可以帮助到大家 另外其它专栏请关注: 锐捷数通实验&…...
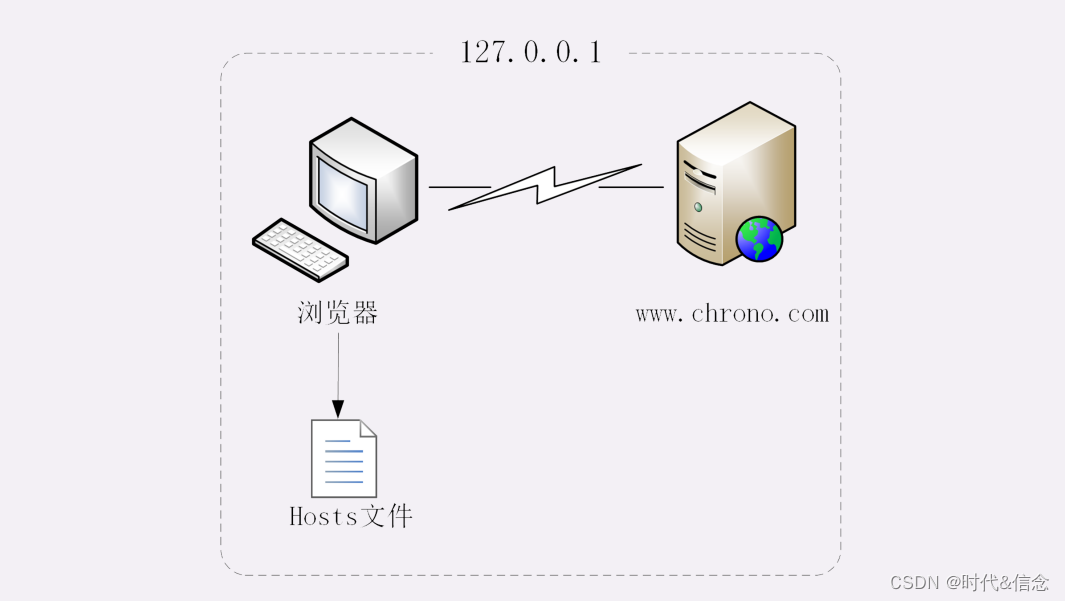
HTTP第六讲——键入网址再按下回车,后面究竟发生了什么?
使用 IP 地址访问 Web 服务器 首先我们运行 www 目录下的“start”批处理程序,启动本机的 OpenResty 服务器,启动后可以用“list”批处理确认服务是否正常运行。 然后我们打开 Wireshark,选择“HTTP TCP port(80)”过滤器,再鼠标…...

layui目录和项目引入
1.目录结构如下 ├─css //css目录 │ │─modules //模块css目录(一般如果模块相对较大,我们会单独提取,比如下面三个:) │ │ ├─laydate │ │ ├─layer │ │ └─layim │ └─layui.css //核心样式文件…...

Ubuntu22.04 将EFI启动分区迁移到另一块硬盘
机器上有两块硬盘, 一块已经安装了Win10, 另一块新装Ubuntu22.04, 在新硬盘上划分分区的时候, 有分出256M给 BOOT EFI, 但是安装的时候没注意, 启动分区不知道怎的跑到 Windows 所在的硬盘上了 记录一下将 /boot/efi 分区迁移至 Ubuntu 所在硬盘, 并创建 Grub 的记录. 预留的…...

只要学会这些AI工具,一个人就是一家营销咨询公司
本教程收集于:AIGC从入门到精通教程 只要学会这些AI工具,一个人就是一家营销咨询公司 随着AI工具的不断涌现,您只需掌握市面上热门的AI工具,便可独自开展营销咨询公司。通过一系列AI工具,您可以为企业提供全案服务,收获丰厚回报。 例如,在协助一家美妆初创公司出海时,…...

[离散数学] 函数
文章目录 函数判断函数的条件复合函数复合函数的性质 逆函数 函数 判断函数的条件 dom F A ⇔ \Leftrightarrow ⇔所有x 都有 F(x)与之对应 有唯一的与其对应 < x , y > ∈ f ∧ < y , z > ∈ f ⇒ y z <x,y>\in f \land <y,z…...

好家伙,又一份牛逼笔记面世了...
最近网传的一些裁员的消息,搞的人心惶惶。已经拿到大厂offer的码友来问我:大厂还能去,去了会不会被裁。 还在学习的网友来问我:现在还要冲互联网么? 我是认为大家不用恐慌吧,该看啥看啥,该学啥…...
基于nodejs+vue3 的高仿网易云音乐
大家好,我是小寻,欢迎大家关注我的公众号:工具优选,加入前端、java群聊哦! 今天给大家分享一个超高水准的项目:基于nodejsvue3研发的高仿网易云音乐,项目内容出自寻码网! 技术栈&a…...
MySQL数据库用户管理以及数据库用户授权
一、数据库用户管理 1、新建用户 CREATE USER 用户名来源地址 [IDENTIFIED BY [PASSWORD] 密码]; ---------------------------------------------------------------------------------------------------------- 用户名:指定将创建的用户名 来源地址:…...

全面分析生物技术的优缺点以及应用场景
一、 引言 生物识别技术具有不可撤销性、高度便利性和较低错误率等优势,在安全领域中也备受瞩目。然而,对于生物识别技术在应对安全挑战方面的可靠性和有效性,但争议并未被完全解决 二、生物识别技术的介绍 所谓生物识别技术就是,…...

OpenAI是什么?
OpenAI是一家人工智能技术公司,成立于2015年,总部位于美国旧金山。它的创始人包括埃隆马斯克等多名知名人士,公司的目标是推进人工智能技术的发展,同时确保人工智能的发展不会对人类造成负面影响。 OpenAI在研究和开发各种人工智能…...

量子计算——新兴领域的前沿技术
随着人类社会文明的不断进步,计算技术也在不断发展。传统计算机在过去的几十年中快速发展,计算速度、存储能力等方面发生了天翻地覆的变化。但随着大数据、人工智能、区块链等新兴领域的迅速崛起,传统计算机的发展似乎面临了瓶颈。在这样的背…...

.Net平台下OpenGL绘制图形(1)(VS2019,Winform,C#)
1、介绍 OpenGL(英语:Open Graphics Library,译名:开放图形库或者“开放式图形库”)是用于渲染2D、3D矢量图形的跨语言、跨平台的应用程序编程接口(API)。这个接口由近350个不同的函数调用组成…...

Casso的创作纪念日
机缘 注册CSDN的时候才刚上大学,到现在使用CSDN已经四年了,距发布第一篇文章却只刚过去一百多天,刚看到这个提醒消息的时候只感慨时间过得真快,自己也在慢慢成长着,当初刚开始学习的时候,查资料用得最多的就…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
