【改进粒子群优化算法】自适应惯性权重粒子群算法(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
1.1 基本粒子群优化算法
1.2 改进粒子群算法
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
文献来源:
1.1 基本粒子群优化算法
基本粒子群算法(BPSO)中,每个优化问题的解都可以看作粒子在搜索空间中的位置,粒子通过飞
行速度决定它们的搜索方向和搜索范围,粒子群通过追随当前群体的最优粒子和自身经历的个体最优位置,调节其飞行速度,在解空间中搜索最优解。粒子群的寻优过程可描述如下:随机初始化粒
子群通过迭代更新群体的速度和位置,在搜索空间中搜寻最优值;每次迭代中,粒子跟踪个体极值和全局极值,利用个体极值和全局极值的信息来调整自身的速度,并以此速度飞行,更新粒子位置。
粒子群第k+1次迭代的更新公式为:

1.2 改进粒子群算法
惯性权重处理。由式(2)可看出,惯性权重w对 PSO 算法的优化性能影响很大。研究表明,
较大的w值有利于跳出局部最优,而较小的w有利于加速收敛。文献[13]提出了单一线性化调整w的策略:随迭代次数的增加而线性减少w,其经验值为[0.9,0.4]。但若采用线性减少w的调整策略,会使得结果不稳定,算法易陷入局部最优。而且,即使能够跳出局部最优,其收敛速度也非常缓慢。原因是单一线性w调整策略采用了统一的权重变化率,使得粒子在整个搜索过程中没有明显差异。因此,本文从收敛速度和搜索范围上对 PSO 进行改进,采用动态改变惯性权重的策略,使得:

a k根据所计算的适应度函数值进行变化,使得传统上随着搜索过程线性减小的w变成随搜索位置的变化而动态改变的w k。w k中充分利用了目标函数的信息,使得搜索方向的精确度得到了启发性加强。
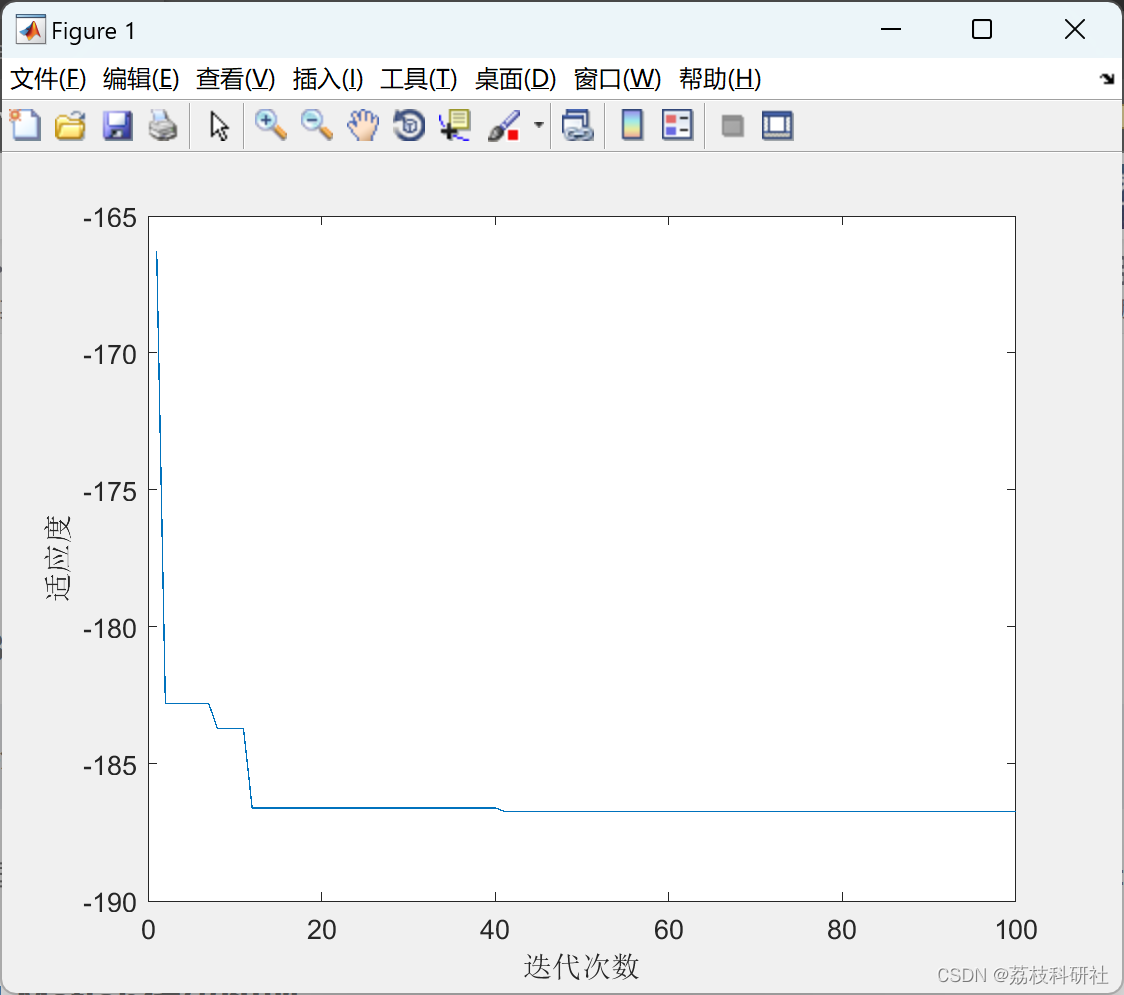
📚2 运行结果

部分代码:
%% PSO Parameters
CostFunction=@(x) CostFun(x); % Cost Function
w=1; % Inertia Weight
wdamp=0.99; % Inertia Weight Damping Ratio
c1=1.5; % Personal Learning Coefficient
c2=2.0; % Global Learning Coefficient
VarSize=[1 nVar]; % Size of Decision Variables Matrix
% Velocity Limits
VelMax=0.1*(VarMax-VarMin);
VelMin=-VelMax;
%% Initialization
empty_particle.Position=[];
empty_particle.Cost=[];
empty_particle.Velocity=[];
empty_particle.Best.Position=[];
empty_particle.Best.Cost=[];
particle=repmat(empty_particle,nPop,1);
GlobalBest.Cost=inf;
for i=1:nPop
% Initialize Position
particle(i).Position=unifrnd(VarMin,VarMax,VarSize);
% Initialize Velocity
particle(i).Velocity=zeros(VarSize);
% Evaluation
particle(i).Cost=CostFunction(particle(i).Position);
% Update Personal Best
particle(i).Best.Position=particle(i).Position;
particle(i).Best.Cost=particle(i).Cost;
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]李国庆,陈厚合.改进粒子群优化算法的概率可用输电能力研究[J].中国电机工程学报,2006(24):18-23.
🌈4 Matlab代码实现
相关文章:

【改进粒子群优化算法】自适应惯性权重粒子群算法(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
ROS 下 激光扫描仪 YDLidar-G4 使用
环境配置: ubuntu20.04 LTS ROS noetic 编程工具:vs code,远程通过ssh访问 扫描仪:YDLidar-G4 YDLidar驱动: YDLidar SDK YDLidar ROS 功能包 此环境包含树莓派,以下过程在树莓派3B上测试通过,…...

智能边缘:数字化时代的关键战略之一
随着物联网、云计算和人工智能等技术的快速发展,智能边缘已经成为了许多企业和组织中的重要部分。智能边缘旨在将物联网设备、应用程序和数据存储集成到一个统一的、移动的计算环境中,以提高效率、降低成本并增强数据安全性。在本文中,我们将…...

EasyRecovery16中文最新版电脑数据恢复软件下载使用教程
EasyRecovery如果需要使用它来恢复数据,请注意,尤其是当需要恢复的数据文件非常重要时,建议使用软件EasyRecovery以保障数据安全。共有三个版本,分别是个人版、专业版、企业版,这三种都可以免费下载并使用,…...
什么是鉴权?这些postman鉴权方式你又知道多少?
一、什么是鉴权? 鉴权也就是身份认证,就是验证您是否有权限从服务器访问或操作相关数据。发送请求时,通常必须包含相应的检验参数以确保请求具有访问权限并返回所需数据。通俗的讲就是一个门禁,您想要进入室内,必须通过…...

最新的经典mysql面试题及答案
互联网产品必然是需要有架构的,架构包含接入层、储蓄层、逻辑处理等等,其中存储层承载着数据落地和持久化的任务,同时给逻辑处理层提供数据查询功能支持。而一提到储蓄层必然就要说数据库了,对于数据库的掌握也是软件工程师面试时…...

算法修炼之练气篇——练气十九层
博主:命运之光 专栏:算法修炼之练气篇 前言:每天练习五道题,炼气篇大概会练习200道题左右,题目有C语言网上的题,也有洛谷上面的题,题目简单适合新手入门。(代码都是命运之光自己写的…...
记录一次Windows7操作系统渗透测试
#本文档仅用于实验,请勿用来使用恶意攻击! 《中华人民共和国网络安全法》中,恶意破坏计算机信息系统罪在第二十七条被明确规定,规定内容为: 第二十七条 任何单位和个人不得为达到破坏计算机信息系统安全的目的&#x…...

承诺协议:定义 构造
文章目录 安全性定义方案构造基于 OWP 存在性基于 DL 假设基于 OWF 存在性基于 DDH 假设 总结 安全性定义 承诺协议(Commitment Scheme)是一个两阶段的两方协议。一方是承诺者(Committer) C C C,另一方是接收者&#…...

二、easyUI中的layout(布局)组件
1.layout(布局)组件的概述 布局容器有5个区域:北、南、东、西和中间。中间区域面板是必须的,边缘的面板都是可选的。每个边缘区域面板都可以通过拖拽其边框改变大小,也可以点击折叠按钮将面板折叠起来。布局可以进行嵌…...

MySQL---聚合函数、字符串函数、数学函数、日期函数
1. 聚合函数 数据准备: create database mydb4; use mydb4;create table emp(emp_id int primary key auto_increment comment 编号,emp_name char(20) not null default comment 姓名,salary decimal(10,2) not null default 0 comment 工资,department char(20…...

边缘计算盒子有哪些?边缘计算应用场景
边缘计算(Edge Computing)是一种分布式计算模型,旨在将数据处理和计算功能从中心数据中心移到数据源附近的边缘设备上。它的目标是在接近数据生成的地方进行实时数据处理和分析,减少数据传输延迟和网络拥塞,提高应用程…...
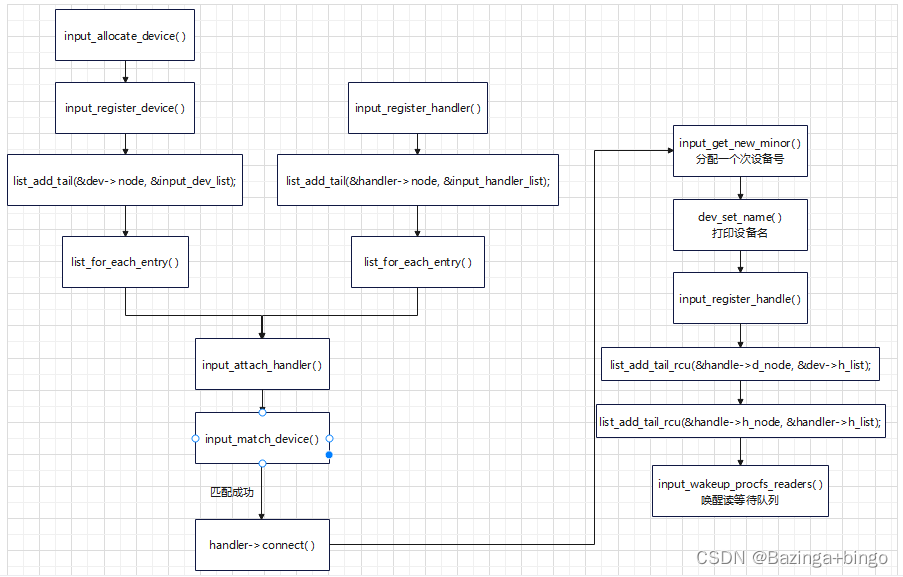
Linux内核(十四)Input 子系统详解 IV —— 配对的input设备与input事件处理器 input_register_handle
文章目录 input_handle结构体详解配对的input设备与input事件处理器实例input核心层对驱动层和事件层之间的框架建立流程图 本文章中与input子系统相关的结构体可参考input子系统结构体解析 input函数路径:drivers/input/input.c input_handle结构体详解 input_ha…...
)
Vue2.x源码解析(三)
Platform 函数 Platform 函数是用于与各种浏览器和平台进行交互的函数,它为 Vue 提供了跨平台的支持,例如浏览器、Node.js 等。Platform 函数提供了一些常用的工具和配置项,例如事件的托管、资源请求和异步更新等。下面是 Platform 函数的伪…...
)
全面理解守护进程的基础概念,以及如何创建一个守护进程(系列文章第三篇)
前言 这个系列的文章有四篇,其目的是为了搞清楚: 进程,shell,shell进程,终端,控制终端,前台进程,后台进程,控制进程,前台进程组,后台进程组&#…...

Leetcode刷题日志5.0
目录 前言: 1.两数相加 2.无重复字符的最长子串 3.整数反转 4.删除链表的倒数第 N 个结点 前言: 今天我又来继续分享最近做的题了,现在开始进入我们快乐的刷题时间吧!(编程语言Python3.0,难度…...

母亲节:向世界上最伟大的母爱致敬
在这世间众多的亲情关系中,有一种关系无与伦比,毫不费力地凌驾于其他任何已知的地球关系之上。这种非凡的关系就是母亲与子女之间的关系。 母亲对家庭无尽的爱、奉献和忠诚使这份感情无价。为了向全球所有母亲表示敬意,母亲节在世界46个国家庆…...
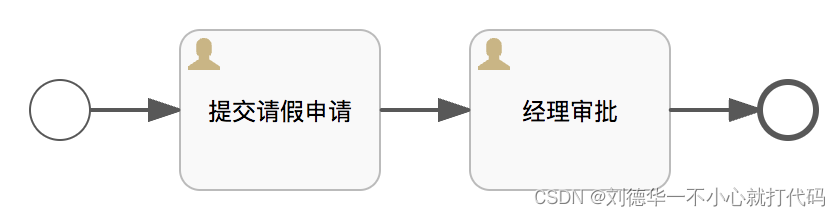
Springboot +Flowable,各种历史信息如何查询(二)
一.简介 正在执行的流程信息是保存在以 ACT_RU_ 为前缀的表中,执行完毕的流程信息则保存在以 ACT_HI_ 为前缀的表中,也就是流程历史信息表。 假设有一个流程,流程图如下: 当这个流程执行完毕后,以 ACT_RU_ 为前缀的…...

DataX下载安装使用
文章目录 01.Clickhouse到HBase(Phoenix)数据导入 DataX介绍下载执行同步的组件配置数据同步查看官方读写配置样例创建Hbase和Phoenix表创建ClickHouse表写入ClickHouse测试数据编写ClickHouse2Hbase配置文件执行同步命令 拓展ClickHouse同步到MySQL配置文件 01.Clickhouse到HB…...
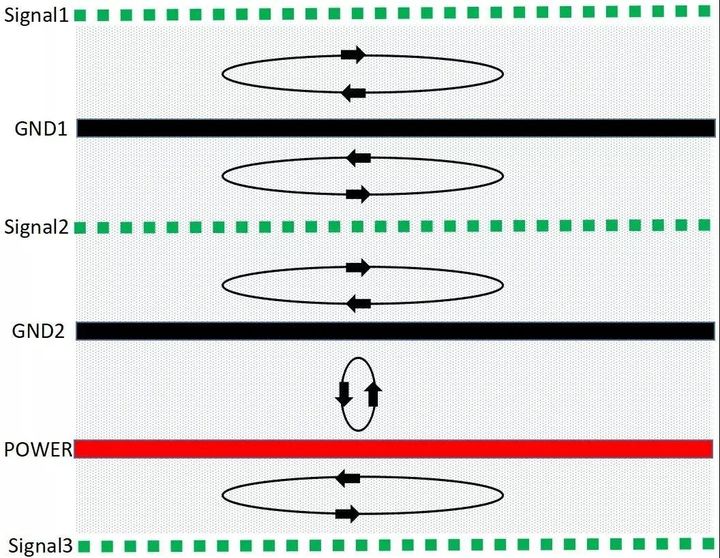
PCB多层板 : 磁通对消法有效控制EMC
在PCB的EMC设计考虑中,首先涉及的便是层的设置;单板的层数由电源、地的层数和信号层数组成;在产品的EMC设计中,除了元器件的选择和电路设计之外,良好的PCB设计也是一个非常重要的因素。 PCB的EMC设计的关键࿰…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

