linux篇【14】:网络https协议
目录
一.HTTPS介绍
1.HTTPS 定义
2.HTTP与HTTPS
(1)端口不同,是两套服务
(2)HTTP效率更高,HTTPS更安全
3.加密,解密,密钥 概念
4.为什么要加密?
5.常见的加密方式
(1)对称加密
(2)⾮对称加密
4. 数据摘要 && 数据指纹
5. 数字签名
6. 理解链 - 承上启下
二.HTTPS 的⼯作过程探究
1.⽅案 1 - 只使⽤对称加密(明⽂传输不可取)
2.⽅案 2 - 只使⽤⾮对称加密(仅单向安全,不可取)
3.⽅案 3 - 双⽅都使⽤⾮对称加密(效率太低不可行)
4.⽅案 4 - ⾮对称加密 + 对称加密(仍有安全问题,见5)
5.中间⼈攻击 - 针对上⾯的场景
6.引⼊证书
(1)CA认证
(2)证书组成
(3)理解数据签名
(4)申请证书过程:
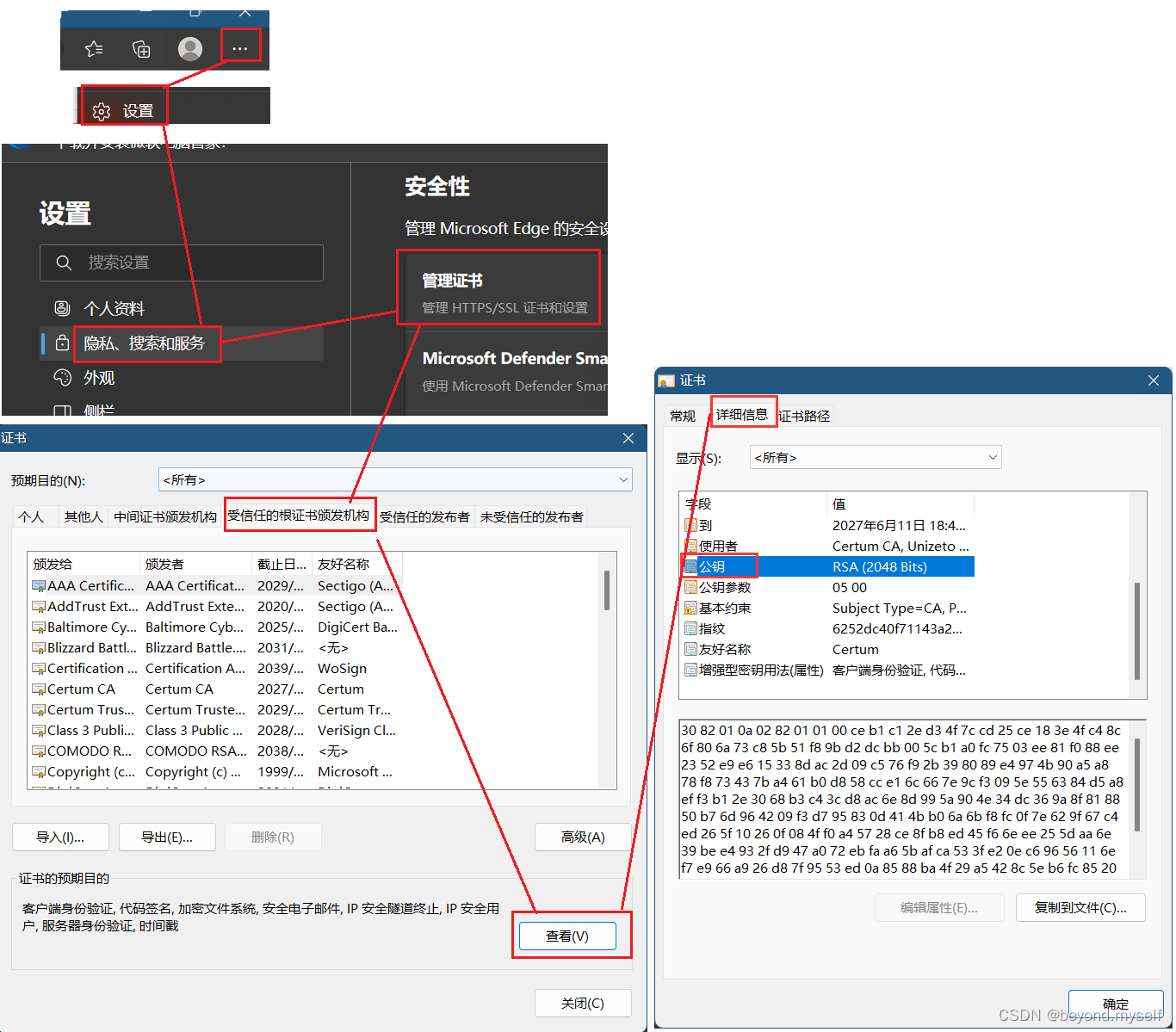
(5)查看浏览器的受信任证书发布机构
编辑
7.⽅案 5 - ⾮对称加密 + 对称加密 + 证书认证
(1)⾮对称加密 + 对称加密 + 证书认证 方案
(2)服务器向客户端发公钥时,中间⼈有没有可能篡改该证书?
(3)中间⼈能否将整个掉包证书?
一.HTTPS介绍
HTTPS 举例:https://new.qq.com/rain/a/20230115A00C3H00
1.HTTPS 定义
2.HTTP与HTTPS
(1)端口不同,是两套服务
(2)HTTP效率更高,HTTPS更安全
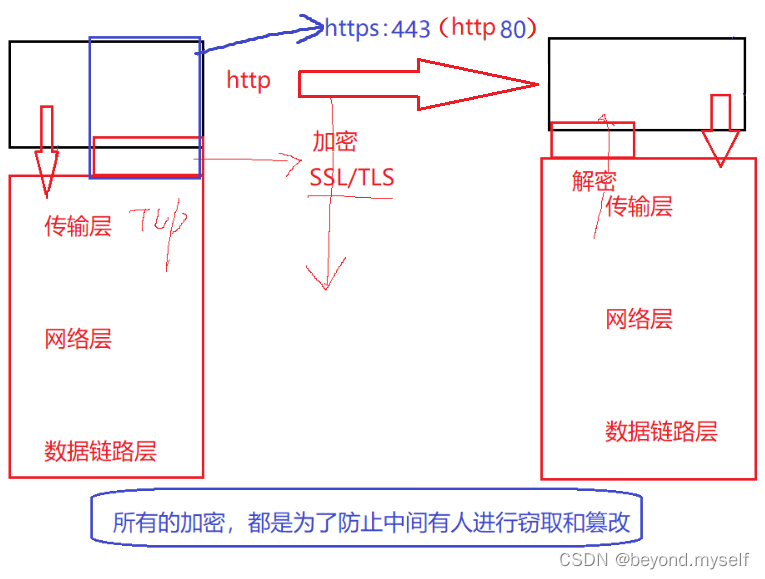
HTTP 不用加密,则效率更高,但是不安全;HTTP 需要加密,则效率相对不高,但是安全;在内网等绝对安全的条件下推荐使用HTTP协议
3.加密,解密,密钥 概念
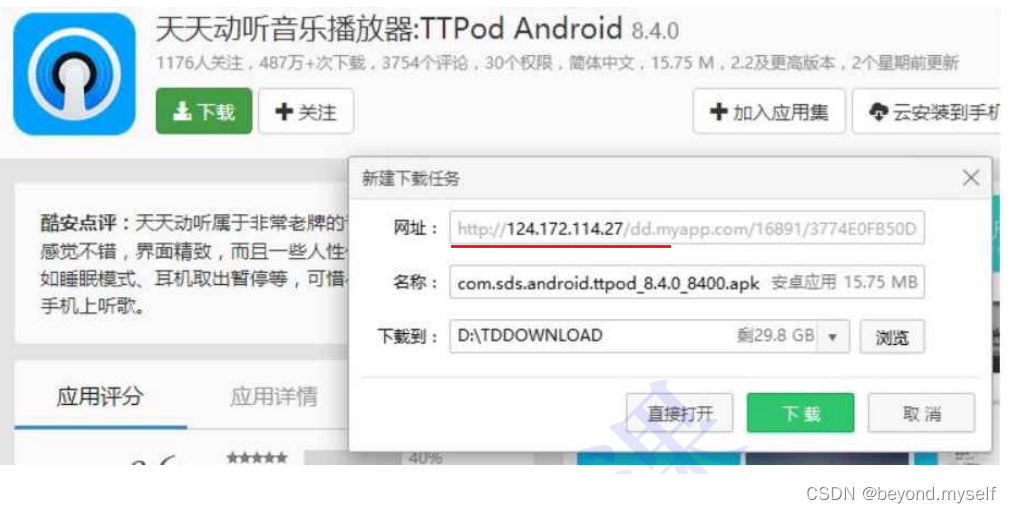
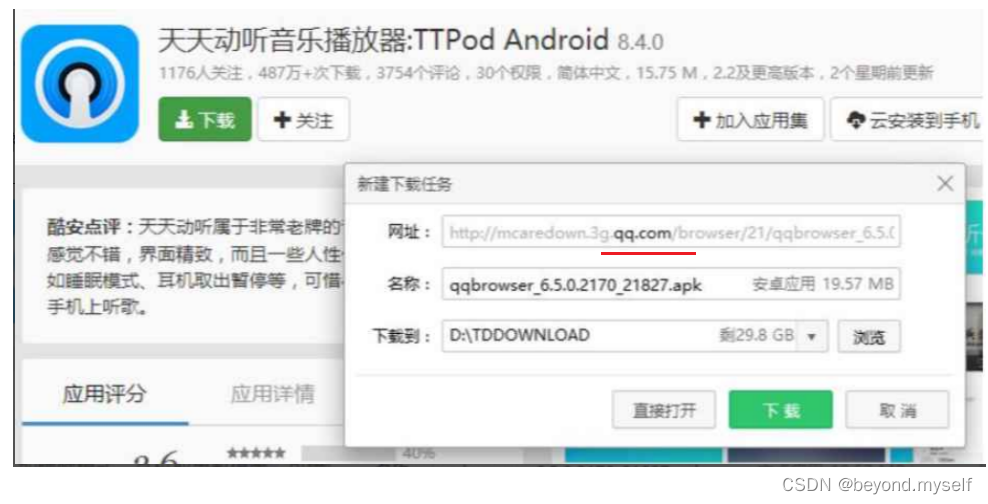
4.为什么要加密?
所有的加密,都是为了防止中间有人进行窃取和篡改
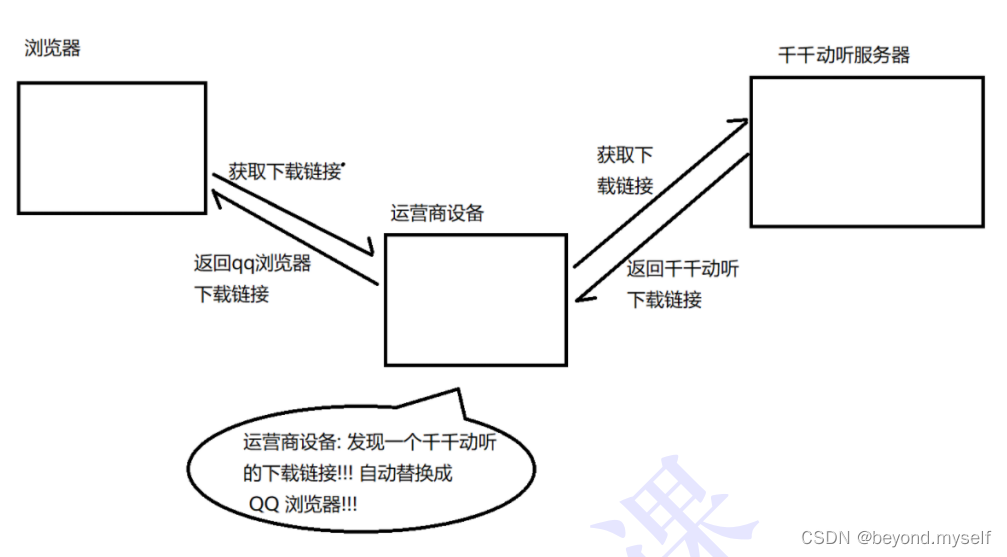
5.常见的加密方式
(1)对称加密
(2)⾮对称加密
4. 数据摘要 && 数据指纹
5. 数字签名
6. 理解链 - 承上启下
二.HTTPS 的⼯作过程探究
1.⽅案 1 - 只使⽤对称加密(明⽂传输不可取)
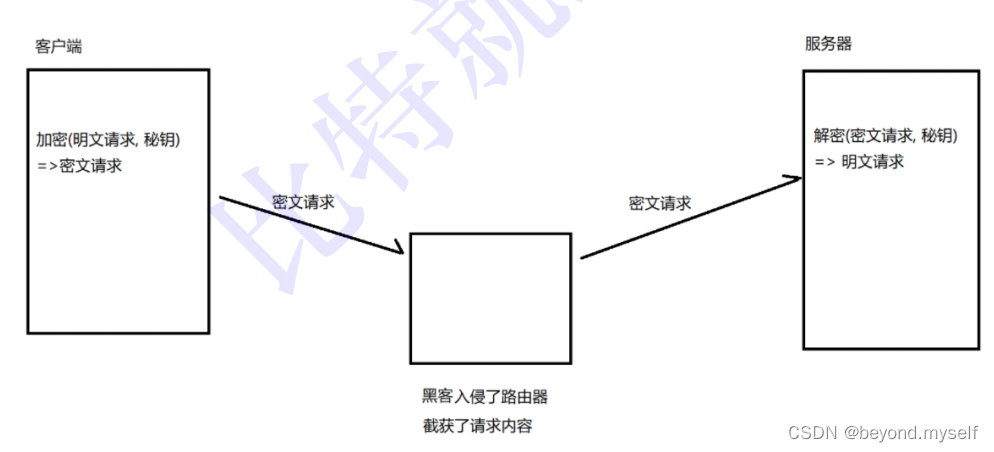
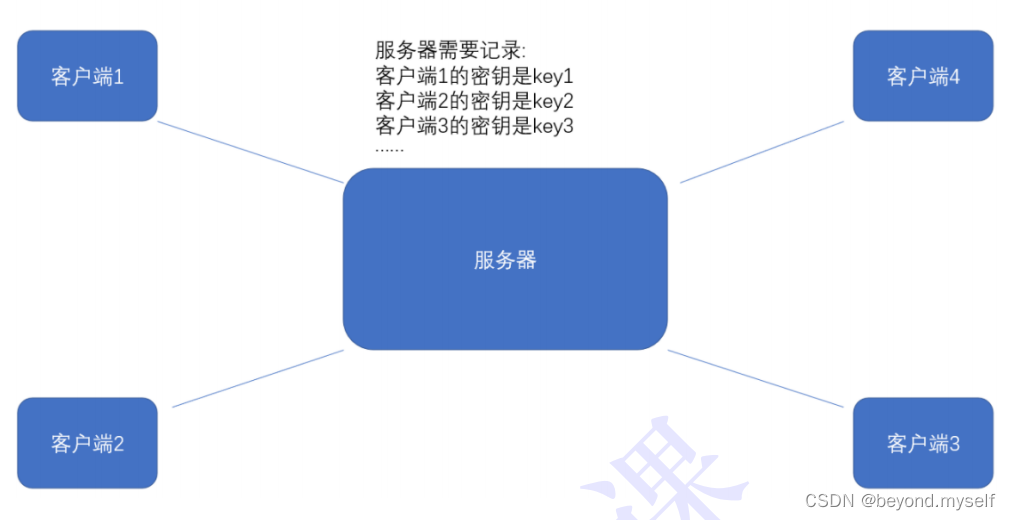
⽐较理想的做法, 就是能在客⼾端和服务器建⽴连接的时候, 双⽅协商确定这次的密钥是啥~
2.⽅案 2 - 只使⽤⾮对称加密(仅单向安全,不可取)
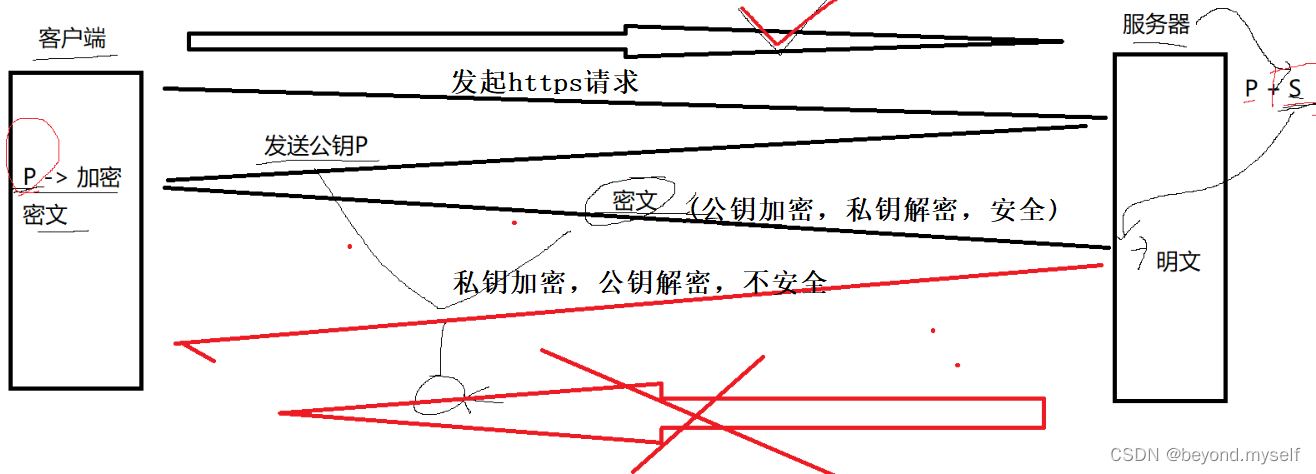
3.⽅案 3 - 双⽅都使⽤⾮对称加密(效率太低不可行)
4.⽅案 4 - ⾮对称加密 + 对称加密(仍有安全问题,见5)
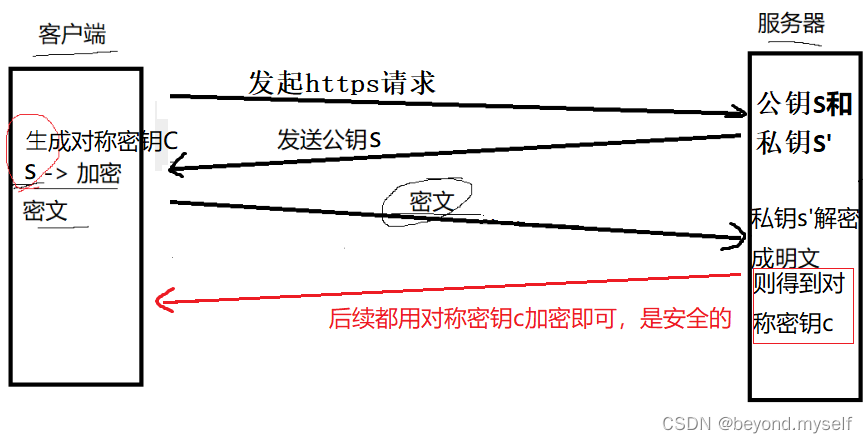
• 服务端具有⾮对称公钥S和私钥S'
5.中间⼈攻击 - 针对上⾯的场景

6.引⼊证书
(1)CA认证

(2)证书组成

(3)理解数据签名
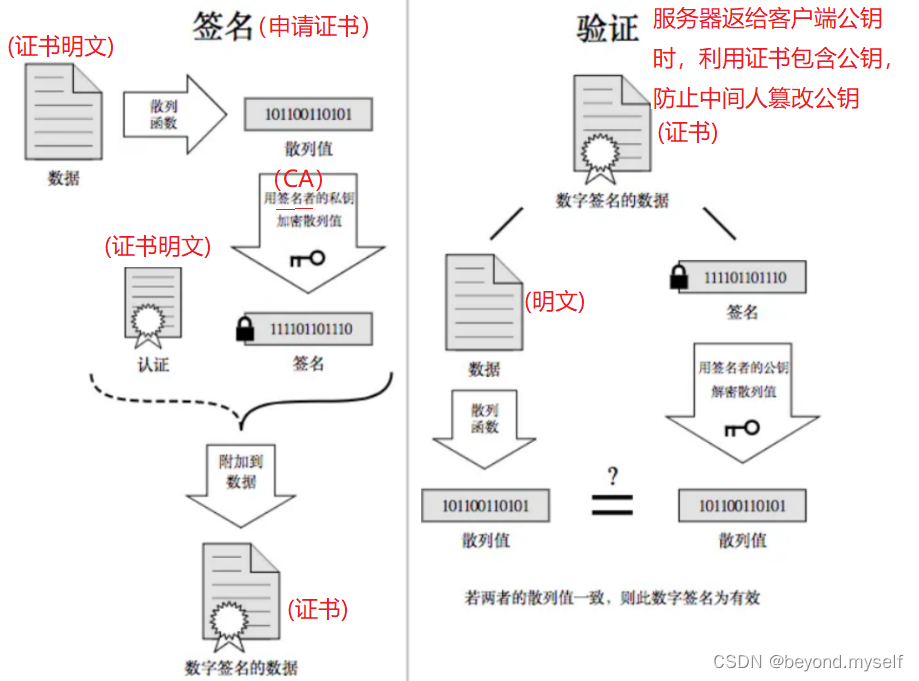
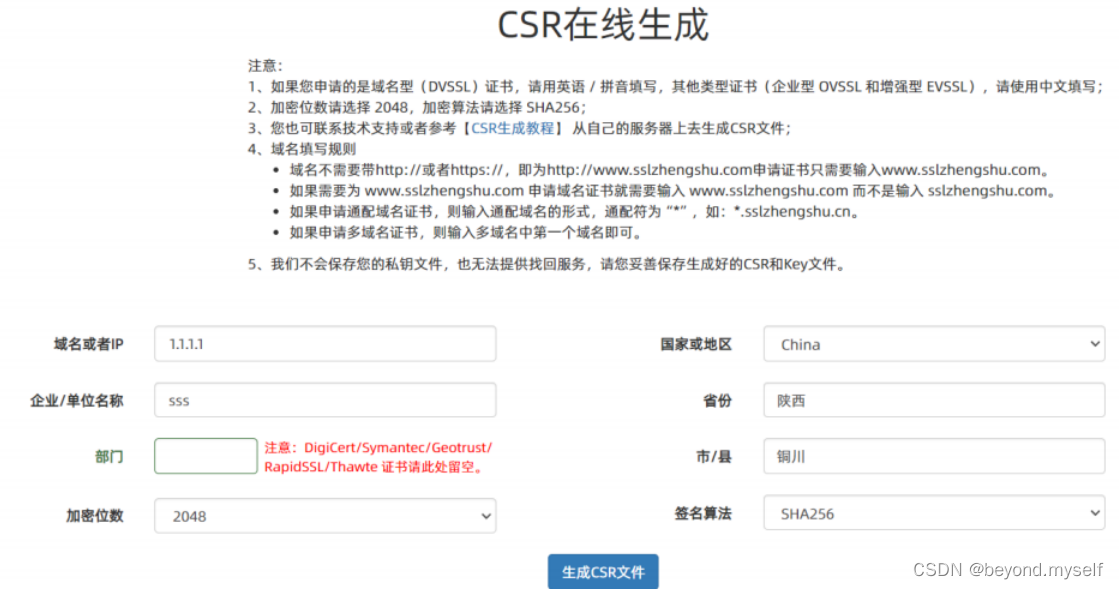
(4)申请证书过程:
当服务端申请CA证书的时候,CA机构会对该服务端进⾏审核,并专⻔为该⽹站形成数字签名,过程如下:

(5)查看浏览器的受信任证书发布机构
7.⽅案 5 - ⾮对称加密 + 对称加密 + 证书认证
(1)⾮对称加密 + 对称加密 + 证书认证 方案
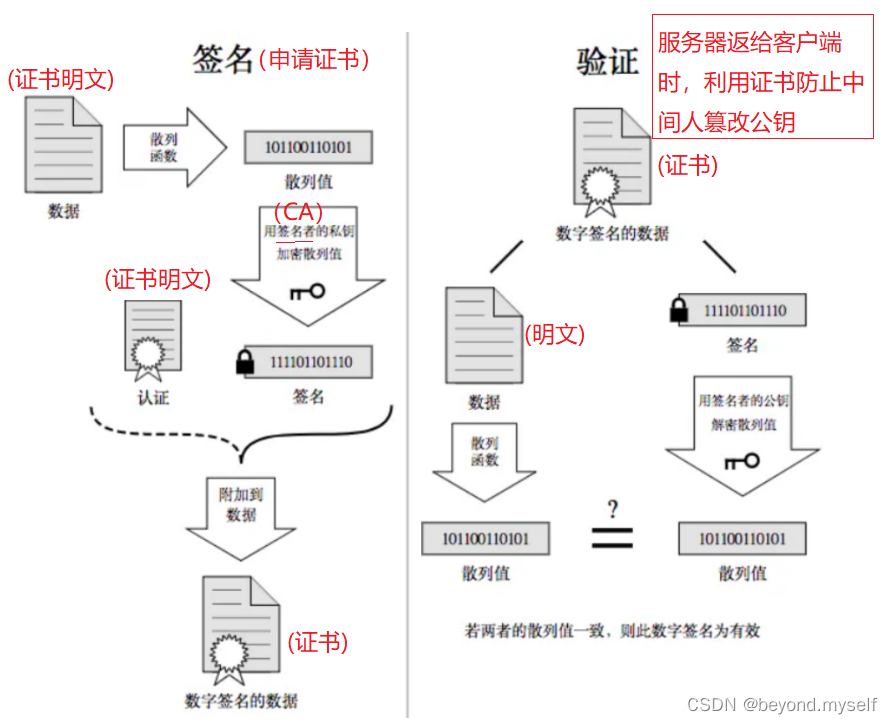
(2)服务器向客户端发公钥时,中间⼈有没有可能篡改该证书?
(3)中间⼈能否将整个掉包证书?
相关文章:

linux篇【14】:网络https协议
目录 一.HTTPS介绍 1.HTTPS 定义 2.HTTP与HTTPS (1)端口不同,是两套服务 (2)HTTP效率更高,HTTPS更安全 3.加密,解密,密钥 概念 4.为什么要加密? 5.常见的加密方式…...

1.9实验9:配置虚链路
1.4.4实验9:配置虚链路 实验目的(1) 实现OSPF 虚链路的配置 (2) 描述虚链路的作用 实验拓扑配置虚链路实验拓扑如图1-19所示。[1] 图1-19 配置虚链路 实验步骤...

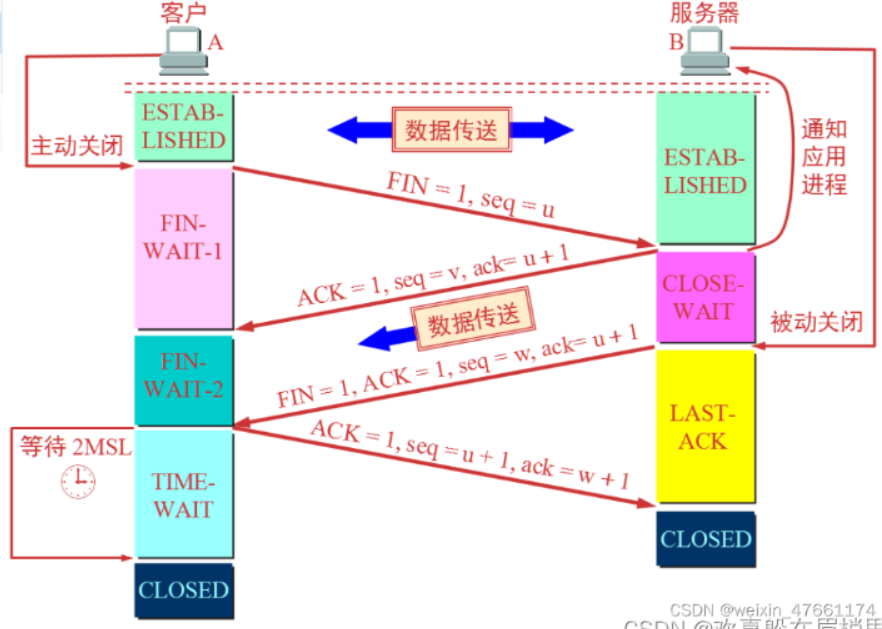
三次握手-升级详解-注意问题
TCP建立连接的过程就是三次握手(Three-way Handshake),在建立连接的过程实际上就是客户端和服务端之间总共发送三个数据包。进行三次握手主要是就是为了确认双方都能接收到数据包和发送数据包,而客户端和服务端都会指定自己的初始…...
软件架构知识3-系统复杂度-高可用性、可扩展性、低成本、安全、规模
高可用性 系统无中断地执行其功能的能力,代表系统的可用性程度,是进行系统设计时的准则之一。 高可用的“冗余”解决方案,单纯从形式上来看,和之前讲的高性能是一样的,都是通过增加更多机 器来达到目的,但…...
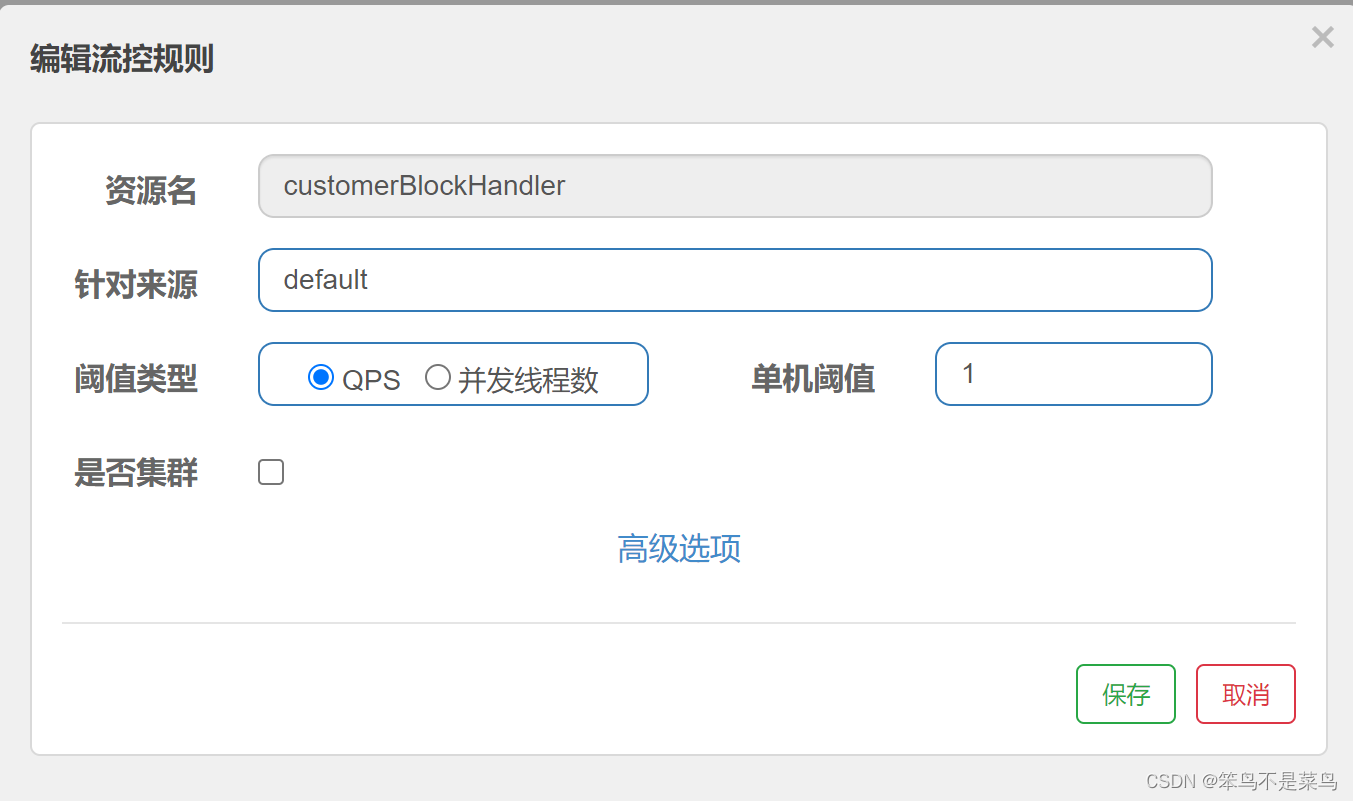
SpringCloud学习笔记 - 自定义及解耦降级处理方法 - Sentinel
1. SentinelRecourse配置回顾 通过之前的学习,我们知道SentinelRecourse配置的资源定位可以通过两种方式实现:一种是URL,另一种是资源名称。这两种限流方式都要求资源ID唯一 RestController public class RateLimitController {GetMapping(…...

Redis之搭建一主多从
搭建redis一主多从的过程 1.在相应位置创建一个文件夹存放redis配置文件 mkdir myredis2.复制redis配置文件到此文件夹中 cp /opt/redis/redis/bin/redis.conf /opt/myredis/redis.conf3.新建三个配置文件 touch redis6379.conf touch redis6380.conf touch redis6381.conf4…...
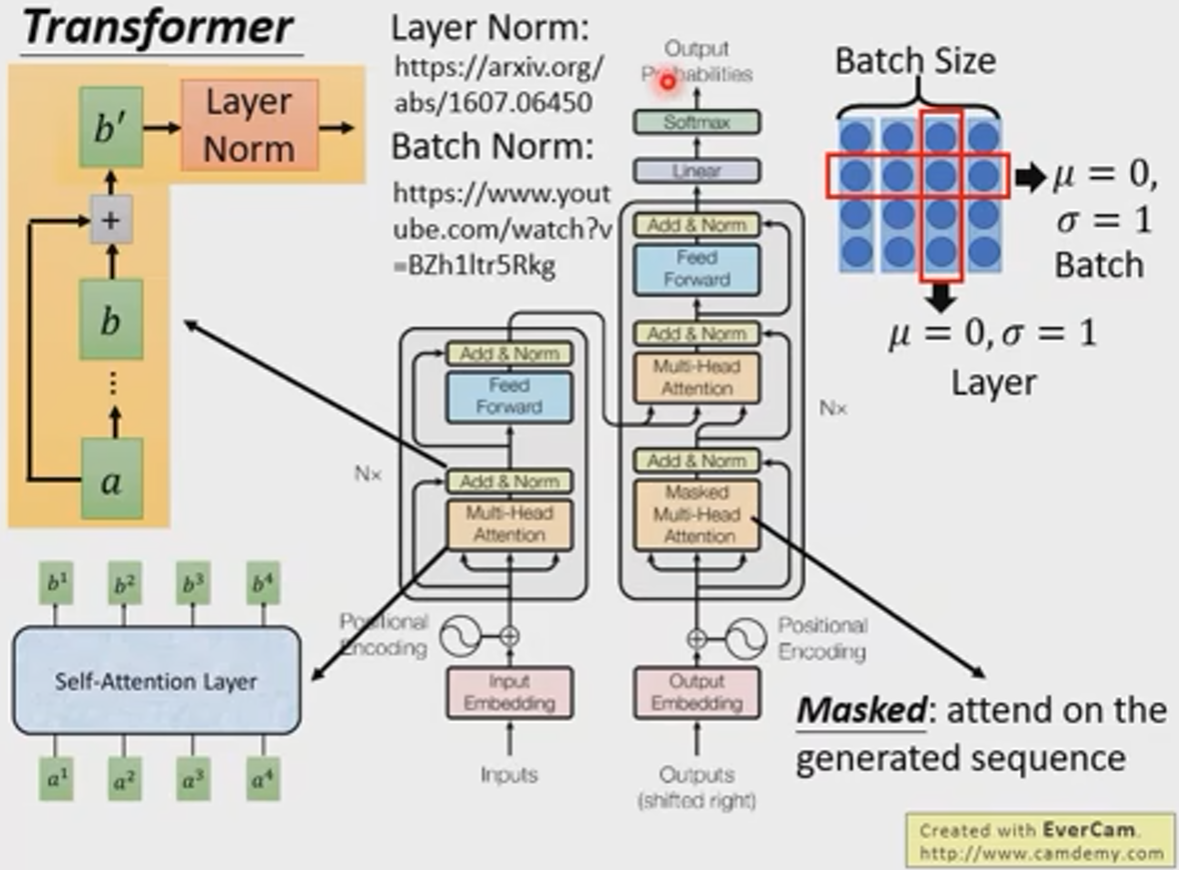
Transformer机制学习笔记
学习自https://www.bilibili.com/video/BV1J441137V6 RNN,CNN网络的缺点 难以平行化处理,比如我们要算b4b^4b4,我们需要一次将a1a^1a1~a4a^4a4依次进行放入网络中进行计算。 于是有人提出用CNN代替RNN 三角形表示输入,b1b^1b1的…...

1、第一个CUDA代码:hello gpu
目录第一个CUDA代码:hello gpu一、__global__ void GPUFunction()二、gpu<<<1,1>>>();三、线程块、线程、网格知识四、核函数中的printf();五、cudaDeviceSynchronize();第一个CUDA代码:hello gpu #include <stdio.h>void cpu(…...
UG二次开发装配篇 添加/拖动/删除组件方法的实现
我们在UG装配的过程中,经常会遇到需要调整组件目录位置,在软件设计过程中可以通过在目录树里面拖动组件来完成。 那么,如果要用程序实现组件的移动/拖动,我们要怎么做呢? 本节就完成了添加/拖动/删除组件方法的实现&…...

【ros bag 包的设计原理、制作、用法汇总】
ros bag 包的设计原理 序列化和反序列化 首先知道Bag包就是为了录制消息,而消息的保存和读取就涉及到一个广义上的问题序列化和反序列化,它基本上无处不在,只是大部分人没有注意到,举个简单的例子,程序运行的时候,是直接操作的内存,也就是一个结构体或者一个对象,但内…...

Linux网络:聚合链路技术
目录 一、聚合链路技术 1、bonding作用 2、Bonding聚合链路工作模式 3、Bonding实现 一、聚合链路技术 1、bonding作用 将多块网卡绑定同一IP地址对外提供服务,可以实现高可用或者负载均衡。直接给两块网卡设置同一IP地址是不可以的。通过 bonding,…...

2023年数据安全的下一步是什么?
IT 预算和收入增长领域是每个年度开始时的首要考虑因素,在当前的世界经济状况下更是如此。 IT 部门和数据团队正在寻找确定优先级、维护和构建安全措施的最佳方法,同时又具有成本效益。 这是一个棘手的平衡点,但却是一个重要的平衡点&#…...
在浏览器输入URL后发生了什么?
在浏览器输入URL并获取响应的过程,其实就是浏览器和该url对应的服务器的网络通信过程。从封装的角度来讲,浏览器和web服务器执行以下动作:(简单流程)1、浏览器先分析超链接中的URL:分析域名是否规范2、浏览器向DNS请求…...
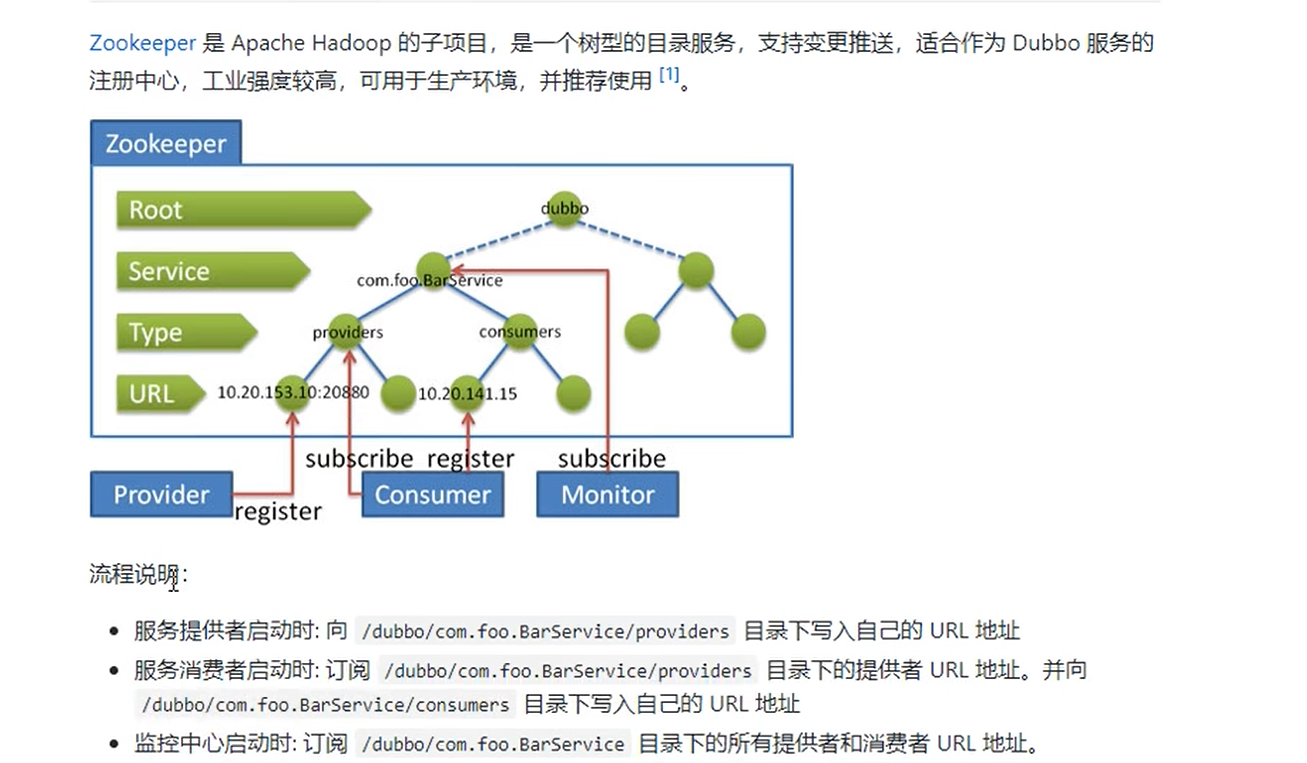
Dubbo学习
0.start 容器container启动(spring),初始化我们的服务提供者(Provider)1.register 把业务层的方法,注册到注册中心(Register)2.subscribe 消费者(Consumer)订…...
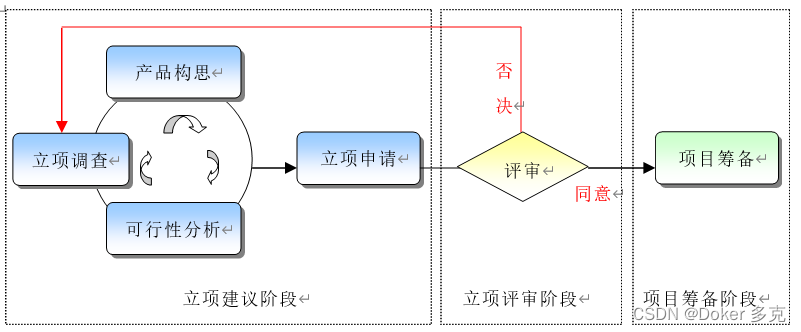
CMMI-立项管理流程
立项管理(Project Initialization Management, PIM)的目的是:(1)采纳符合机构最大利益的立项建议,通过立项管理使该建议成为正式的项目(即合法化)。(2)杜绝不…...

看《狂飙》读人生,致敬2023!
作为2023年的第一篇博文,我不想写代码,我想谈谈最近看的《狂飙》,总结了十条哲理,共勉。希望我们的2023,未来的人生会更加出彩。 01 你以为很好的关系,其实也就那么回事。 陈金默以为高启强对他很好&…...

Web自动化测试——Junit5篇
文章目录一、相关依赖注入二、注解调用三、断言 Assert四、规定用例执行顺序五、高效参数化1)单参数2)多参数3)文件获取参数4)方法获取数据(动态参数)六、测试套件整活Junit 是一个面向 Java 语言的单元测试…...
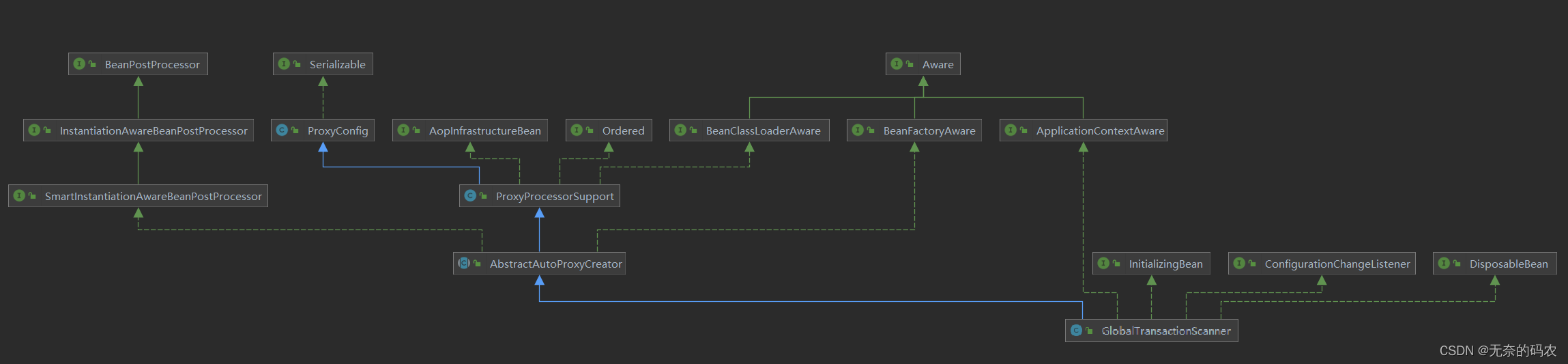
Seata源码学习(二)-源码入口
Seata源码剖析-源码入口 Seata客户端启动 首先一个Seata的客户端启动一般分为几个流程: 自动加载各种Bean及配置信息初始化TM初始化RM(具体服务)初始化分布式事务客户端完成,代理数据源连接TC(Seata服务端ÿ…...

2023如何选购适合游戏设计的电脑硬件
游戏设计涉及许多不同的学科,因此涉及许多不同的软件包。有游戏引擎本身,例如 Unreal Engine 和 Unity,以及 3D 设计软件,例如 3ds Max、Blender 和 ZBrush——等等!大多数软件开发人员都维护着这些不同应用程序的系统…...

springboot maven项目集成阿里p3c-pmd插件使用
阿里巴巴规约使用的是pmd代码静态分析工具,通过maven-pmd-plugin这个maven插件实现。 pom文件引入 <!-- 阿里p3c插件 --> <plugin><groupId>org.apache.maven.plugins</groupId><artifactId>maven-pmd-plugin</artifactId><…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...

Qwen系列之Qwen3解读:最强开源模型的细节拆解
文章目录 1.1分钟快览2.模型架构2.1.Dense模型2.2.MoE模型 3.预训练阶段3.1.数据3.2.训练3.3.评估 4.后训练阶段S1: 长链思维冷启动S2: 推理强化学习S3: 思考模式融合S4: 通用强化学习 5.全家桶中的小模型训练评估评估数据集评估细节评估效果弱智评估和民间Arena 分析展望 如果…...