洛谷P1157详解(两种解法,一看就会)
一、问题引出
组合的输出
题目描述
排列与组合是常用的数学方法,其中组合就是从 n n n 个元素中抽出 r r r 个元素(不分顺序且 r ≤ n r \le n r≤n),我们可以简单地将 n n n 个元素理解为自然数 1 , 2 , … , n 1,2,\dots,n 1,2,…,n,从中任取 r r r 个数。
现要求你输出所有组合。
例如 n = 5 , r = 3 n=5,r=3 n=5,r=3,所有组合为:
123 , 124 , 125 , 134 , 135 , 145 , 234 , 235 , 245 , 345 123,124,125,134,135,145,234,235,245,345 123,124,125,134,135,145,234,235,245,345。
输入格式
一行两个自然数 n , r ( 1 < n < 21 , 0 ≤ r ≤ n ) n,r(1<n<21,0 \le r \le n) n,r(1<n<21,0≤r≤n)。
输出格式
所有的组合,每一个组合占一行且其中的元素按由小到大的顺序排列,每个元素占三个字符的位置,所有的组合也按字典顺序。
注意哦!输出时,每个数字需要 3 3 3 个场宽。以 C++ 为例,你可以使用下列代码:
cout << setw(3) << x;
输出占 3 3 3 个场宽的数 x x x。注意你需要头文件 iomanip。
样例 #1
样例输入 #1
5 3
样例输出 #1
1 2 31 2 41 2 51 3 41 3 51 4 52 3 42 3 52 4 53 4 5
二、解法一:拼接字符串,然后再cout
毫无疑问,这题肯定是深度优先搜索就能解决的问题,但与普通题目存在的一个不同点就是如何去按题中所述的要求去输出,在方法一当中我采用的是拼接字符串的方式,示意图如图所示:图中的cout并不是真正的cout,而是为了起一个示意的作用,由于篇幅有限,因此我只画出了一个深度方向上的。

有一个需要注意的点是,题中要求的是set(w)为3并按右对齐输出,由于我们这里是用字符串拼接的方式进行的,因此需要注意当数字为1位的时候我们要加2个空格,当数字为2位时加1个空格,代码如图所示:
#include <iostream>
#include <iomanip>
using namespace std;
int n,r,a[22];
void dfs(int m,string s,int startx)
{if (m==r){cout<<s<<endl;return;}for (int i = startx; i <= n; i++){string t;if (a[i]>9){t=" "+to_string(a[i]);}else{t=" "+to_string(a[i]);}dfs(m+1,s+t,i+1);}return;
}
int main()
{cin>>n>>r;for (int i = 1; i <= n; i++){a[i]=i;}dfs(0,"",1);
}
解法二:直接cout
直接cout时,虽然仍是采用深度优先的方式,但细节相比于上面就要做出改变了,

在此解法当中,我们的dfs函数当中的变量m充当了解法一当中变量m的作用,只不过我们此时是从1开始的(因为我们需要访问a[k-1],所以为了防止数组越界,k的值必须从1开始),此外我们的数组a的作用也与解法一有很大的不同:解法一的数组a是写死的,起一个访问元素的作用,但在此解法当中是动态变化的 ,并在每一步当中都对其赋予当前值。最终当我们成功访问了r个元素的时候我们就输出。
代码如下:
#include <iostream>
#include <iomanip>
using namespace std;
int n,r;
int a[22];
void dfs(int k)
{if(k>r){for (int i = 1; i <= r; i++){cout<<setw(3)<<a[i];}cout<<endl;return;}for (int i = a[k-1]+1; i <= n; i++){a[k]=i;dfs(k+1);}
}
int main()
{cin>>n>>r;dfs(1);
}
相关文章:

洛谷P1157详解(两种解法,一看就会)
一、问题引出 组合的输出 题目描述 排列与组合是常用的数学方法,其中组合就是从 n n n 个元素中抽出 r r r 个元素(不分顺序且 r ≤ n r \le n r≤n),我们可以简单地将 n n n 个元素理解为自然数 1 , 2 , … , n 1,2,\dot…...

JavaScript异步编程和回调
目录 1、编程语言中的异步 2、JavaScript 3、回调 3.1在回调中处理错误 3.2回调的问题 3.2回调的替代方案 1、编程语言中的异步 默认情况下,JavaScript是同步的,并且是单线程…...

Qt开发笔记(Qt5.9.9下载安装环境搭建win10)
#1 Qt下载网站(国内、国外镜像) #2 Qt5.9.9安装选项 #3 配置系统环境变量 #4 创建测试项目 #1 Qt下载网站(国内、国外镜像) 官方下载地址(慢):http://download.qt.io/ 国内镜像网站 这里给大家…...
使用Plist编辑器——简单入门指南
本指南将介绍如何使用Plist编辑器。您将学习如何打开、编辑和保存plist文件,并了解plist文件的基本结构和用途。跟随这个简单的入门指南,您将掌握如何使用Plist编辑器轻松管理您的plist文件。 plist文件是一种常见的配置文件格式,用于存储应…...

Python常用的开发工具合集
Python是一种功能强大且易于学习的编程语言,被广泛应用于数据科学、机器学习、Web开发等领域。随着Python在各个领域的应用越来越广泛,越来越多的Python开发工具也涌现出来。但是,对于新手来说,选择一款合适的Python开发工具可…...

机器学习之线性回归
往期目录 python在线性规划中的应用 文章目录 一、线性回归算法概述1.1 什么是线性回归?1.2 线性回归算法原理1.3 线性回归的应用场景 二、线性回归算法Python实现2.1 导入必要的库2.2 随机生成数据集2.3 拟合模型2.4 预测结果2.5 结果可视化 三、完整代码 线性回归…...

中国系统正式发声!所有用户永久免费,网友:再见了,CentOS!
点关注公众号,回复“1024”获取2TB学习资源! 如果说:没有操作系统会怎么样? 对于个PC来说,无论是台式机、笔记本、平板等等,一切都变的一无是处,这些硬件对我们来说,和一堆废铁没什么…...

Oracle数据库坏块类故障
正常的数据块有其特有的固定格式,如果某数据块内部出现了混乱而导致Oracle无法读取,则可称其为坏块。数据库坏块的影响范围可大可小,严重时会导致数据库无法打开。当数据库出现坏块时,一般出现ORA-01578错误、ORA-10632错误或者OR…...

andorid之摄像头驱动流程--MTK平台
camera成像原理: 景物通过镜头生产光学图像投射到sensor表面上,然后转为模拟电信号,经过数模变成数字图像信号,在经过DSP加工出来,然后在通过IO接口传输到CPU处理。 由于摄像头满足总线、驱动、设备模型,…...

Android9.0 iptables用INetd实现屏蔽ip黑名单的实现
1.前言 在9.0的系统rom定制化开发中,在system中netd网络这块的产品需要中,会要求设置屏蔽ip地址之内的功能,liunx中iptables命令也是比较重要的,接下来就来在INetd这块实现屏蔽ip黑名单的的相关功能,就是在app中只能屏蔽某个网址,就是除了这个网址,其他的都能上网,最后…...

介绍一下json
目录 介绍一下json Elasticsearch7.6学习指南 介绍一下json JSON(JavaScript Object Notation)是一种轻量级的数据交换格式,它以易于阅读和编写的文本形式表示结构化数据。JSON最初是由Douglas Crockford在2001年提出的,它在we…...

DI依赖注入环境
1.构造器注入 上一章节已经说过了: <?xml version"1.0" encoding"UTF-8"?> <beans xmlns"http://www.springframework.org/schema/beans"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLoca…...

《程序员面试金典(第6版)》面试题 16.18. 模式匹配(暴力破解 + 剪枝)
题目描述 你有两个字符串,即pattern和value。 pattern字符串由字母"a"和"b"组成,用于描述字符串中的模式。 例如,字符串"catcatgocatgo"匹配模式"aabab"(其中"cat"是"a&q…...
一天吃透SpringCloud面试八股文
1、什么是Spring Cloud ? Spring cloud 流应用程序启动器是基于 Spring Boot 的 Spring 集成应用程序,提供与外部系统的集成。Spring cloud Task,一个生命周期短暂的微服务框架,用于快速构建执行有限数据处理的应用程序。 Sprin…...

java生成图片缩略图
目录 前言一、使用Base64编码方式1、基本方法2、压缩本地图片保存到本地3、压缩网络图片到图片服务器 二、使用thumbnailator工具方式1、导入依赖2、压缩本地图片保存到本地 前言 下面介绍了两种获取图片缩略图的方式,全都不是一次性压缩,如果没有达到设…...
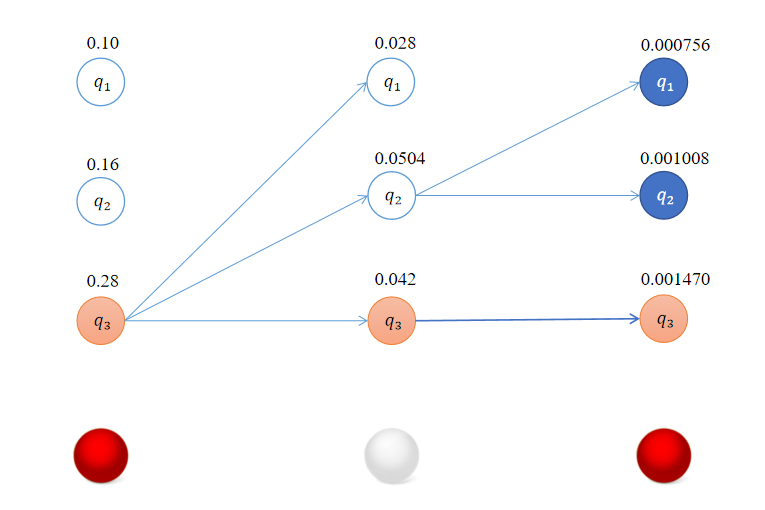
《统计学习方法》——隐马尔可夫模型(下)
学习算法 HMM的学习,在有观测序列的情况下,根据训练数据是否包含状态序列,可以分别由监督学习算法和无监督学习算法实现。 监督学习算法 监督学习算法就比较简单,基于已有的数据利用极大似然估计法来估计隐马尔可夫模型的参数。…...

Liunx top 命令详解
文章目录 top补充说明语法选项top交互命令实例 top 显示或管理执行中的程序 补充说明 top命令 可以实时动态地查看系统的整体运行情况,是一个综合了多方信息监测系统性能和运行信息的实用工具。通过top命令所提供的互动式界面,用热键可以管理。 语法…...

基于 SpringBoot 的医院固定资产系统
本文将介绍基于 SpringBoot 技术的医院固定资产系统的设计和实现。医院固定资产管理是医疗机构管理工作的重要组成部分,它对医院的正常运营和管理具有重要的意义。本系统的设计和实现将有助于医疗机构更好地管理和维护其固定资产。 1. 系统需求分析 医院固定资产管…...

【企业信息化】第2集 免费开源ERP: Odoo 16 销售管理系统
文章目录 前言一、概览二、使用功能1.通过清晰报价提高销售效率2.创建专业报价单3.管理订单及合同4.简化沟通5.维护产品&价格6.直观的报告7.集成 三、总结 前言 世界排名第一的免费开源ERP: Odoo 16 销售管理系统。通过Odoo Sign应用程序和在线支付,发送报价。…...

浅谈数据治理
大家好 ,近年来,数据治理成为挖掘数据价值的重要手段和工具。随着大数据平台和工业互联网兴起,数据治理平台主要采用数据中台技术和微服务架构初步替代传统架构,面向大数据架构下,为数据资源中心与外部数据系统提供数据…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...
