从洛克菲勒思想中洞悉的财富秘密
超友们,早上好~
🙆 今天我为你带来的分享是《从洛克菲勒思想中洞悉的财富秘密》,主要分为两个部分:
-
一、【洛克菲勒的 10 大底层心法】
-
二、【洛克菲勒工作的 6 大原则】
如何从贫穷通往富裕?
「始终把这句话放到第一位:我就是我最大的资本。」
那么,20 世纪的美国首富石油大王洛克菲勒是如何把这句话贯彻到底的呢?
✅一、【洛克菲勒的 9 大底层心法】
1、『建立价值思维』🍒
交易的真谛是交换价值,即用别人想要的东西来换取你想要的东西。
因此,要完成一笔好的交易,最好的方法就是强调其价值。
2、『重视环境的力量』🍒
人是环境的产物,环境的作用远超你的想象,因此要多接近积极成功的人,少同消极的人来往。
3、『培养自信和勇气』🍒
幸运儿之所以幸运,是源自于他们的自信和勇气,而非幸运本身。
「拥有十足的自信心非常重要,只要我们百分之两百地笃信“我能做到”时,就会想出“如何解决”的方法。」
「只有拥有强大的自信,先充分地相信自己是一个很重要的人物,别人才会跟着这么认为。」
「如果你自己都觉得比不上别人,你就会表现出“真”的比不上别人的各种行动,因为你的思想会决定你的行为。」
4、『利用反动力』🍒
「他人的奚落和侮辱并非是坏事,它会给你一股强大的动力,如同排山倒海,催你奋进,催你成就更强大的自己。」
5、『建立强者思维』🍒
「面对那些不看好自己的人,只有不断地强化自身,让自己变得强大,才是对它最好的羞辱与反击。」
唯有成为强者才能赢得尊重,如果你不能成为一名强者,你就很难去审视这个世界,去真实地理解这个世界。
而成为强者,就必须要有野心,因为人活着就得有野心或目标,否则,就会像一艘没有舵的船,永远漂流不定,只会到达失望与丧气的海滩。
怎样才算有野心?
「即具有永不满足的心态,你要变强,甚至更强,唯有如此,你才能得到自己想要的一切。」
6、『保持乐观』🍒
乐观是一种信念,始终相信生活终究是乐多苦少,始终相信即使不如人愿的事屡屡发生,好事终将占得上风。
7、『学会装傻』🍒
「越是聪明的人越有装傻的必要,正如越是成熟的稻子,越垂下稻穗那样,装傻(即摆低姿态,变得谦虚)带给你的好处很多很多,所以聪明人一定要学会装傻。」
8、『情绪管理』🍒
修炼自己管理情绪的能力,在做决策时要完全根据需要来做决定,避免感情用事,要永远知道自己真正想要的是什么。
9、『心态至上』🍒
「如何对待工作本质上就是心态问题。」
「态度决定了我们的行动,行动影响了工作的结果,而结果又关乎我们的前程。」
「所以,从一开始,我们就要端正自己的态度,只有把心态放正,我们的人生道路才能越走越顺。」
✅二、【洛克菲勒工作的 6 大原则】
1、『构建工作的原动力』🍒
如果我们不能将时间投入到自己喜爱的事情上,就无法感到自我满足;
如果得不到自我满足,我们就将失去生活的热情;
如果失去了生活的热情,那就会失去工作的动力。
所以真正的重点是——「找到那些你喜爱又能给别人创造价值的事情,然后慢慢地想办法将其培养起来。」
2、『养成正确的做事态度』🍒
做事的态度很重要,那什么才是好的做事态度?
「做决定之前,冷静地思考与决策,一旦做出决定,就马上义无反顾地执行到底。」
当我们面对同一个问题的时候,正确的态度是:「力求找出更多不同的解决方案,最后从中选出投入产出比最优的方案,而这,也是大部分成功者赚到大钱的秘密。」
3、『一段时间专注于一件事』🍒
人生中最令人感到挫折的,莫过于——「想做的事太多,结果不但没有足够的时间去做,反而想到每件事的步骤都如此的繁多,而被做不到的情绪所震慑,以致最后一事无成。」
而智者的应对策略是:「做减法」。
即从 10 件事情中选出 3 件最重要的事,最后再从这 3 件事情中选出最重要的 1 件事,然后把你大部分的精力都聚焦于这 1 件事情,把它做到极致。
4、『培养解决问题的能力』🍒
在这个时代,解决问题的能力是非常重要的,这毋庸置疑,那么,我们如何才能提升这种具有竞争力的稀缺能力呢?
唯有持续不断地探索,发现更多更好的解决方案去应对问题。
「面对已完成的任务,要进行及时复盘,以求发现更好的解决思路或方案。」
「面对难以完成的任务,要善于切换思路,另辟蹊径寻求应对方法。」
5、『了解最少必要知识之后就马上行动』🍒
「起点可能影响结果,但不会决定结果,我们的命运是由我们的行动所决定的,绝非出身。」
「在开始做一件事情之前,无论你事前做了多少准备、思考了多久,思考地多深多系统多全面,当你真正着手开始做的时候,都难免会犯错误。」
所以,更好的策略是——「在掌握了做这件事的最少必要知识之后,就马上去行动。」
然后,「在行动中思考,行动后复盘总结,接着再用改善后的行动方案去进行新一轮的行动,如此往复,即可不断向卓越靠近。」
6、『追求卓越』🍒
《一生的财富》的作者曾说过:财富与目标是成正比的。
如果你胸怀大志、目标高远,你的财富之山就将垒向云霄。
「如果你只想得过且过,那你就只有做末流鼠辈的分儿了,甚至一事无成,即使财富离你近在咫尺,你也只会获得很少的一点点而已。」
所以,无论何时,「都应该把追求卓越作为人生信条,因为在未来时代里,第二名跟最后一名其实没什么两样。」
公钟号同名,欢迎关注~
参考链接:
-
1、《一生的财富》:https://book.douban.com/subject/27045965/
-
2、《通往财富自由之路》:https://book.douban.com/subject/30371975/
相关文章:

从洛克菲勒思想中洞悉的财富秘密
超友们,早上好~ 🙆 今天我为你带来的分享是《从洛克菲勒思想中洞悉的财富秘密》,主要分为两个部分: 一、【洛克菲勒的 10 大底层心法】 二、【洛克菲勒工作的 6 大原则】 如何从贫穷通往富裕? 「始终把这…...
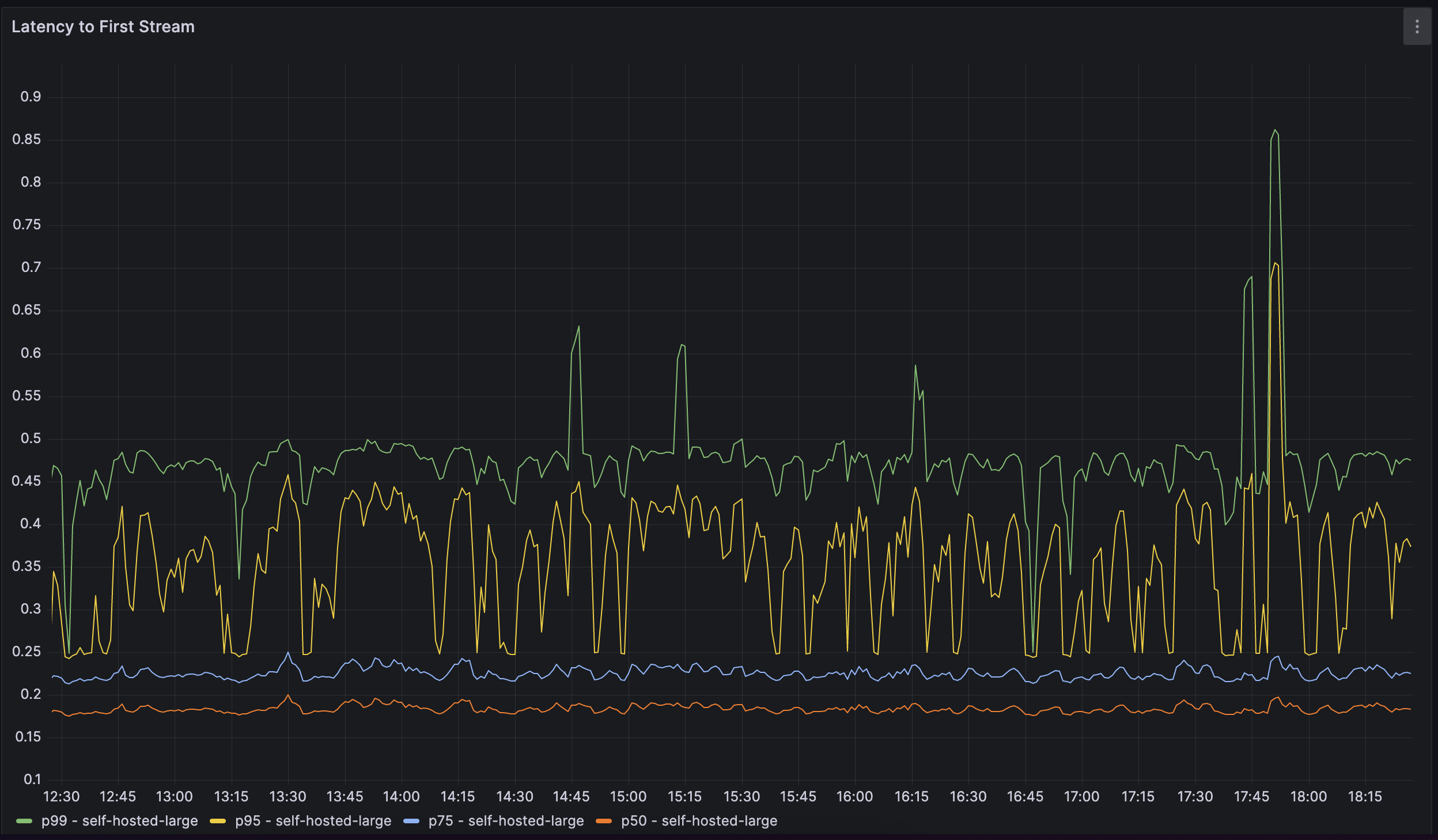
如何训练自己的大型语言模型
如何使用 Databricks、Hugging Face 和 MosaicML 训练大型语言模型 (LLM) 介绍 大型语言模型,如 OpenAI 的 GPT-4 或谷歌的 PaLM,已经席卷了人工智能世界。然而,大多数公司目前没有能力训练这些模型,并且完全依赖少数大型科技公司…...

Java中的SLF4J是什么?如何使用SLF4J进行日志管理
在Java开发中,日志管理是一个非常重要的问题。日志管理可以帮助开发人员更好地了解应用程序的运行情况,以及快速诊断和解决问题。而SLF4J是Java中最常用的日志管理框架之一。在本文中,我们将详细介绍SLF4J的概念和使用方法。 什么是SLF4J&am…...

PHP程序员面对的压力大不大?我来聊聊程序员转行的就业方向
作为一名程序员,不同领域、不同公司和不同项目所面对的压力程度可能会有所不同。但是,一般来说,程序员需要长时间专注于编写代码,需要不断学习和适应新的技术和变化,还需要在项目的压力下保证工作的质量和进度。因此&a…...
)
牛客网专项练习Pytnon分析库(十)
1.Python Pandas处理缺失值,以下哪个选项是对缺失值NaN进行删除操作(C)。 A.isnull B.notnull C.dropna D.fillna 解析: A选项,Isnull()返回表明哪些值是缺失值的布尔值; B选项,notnull()返…...
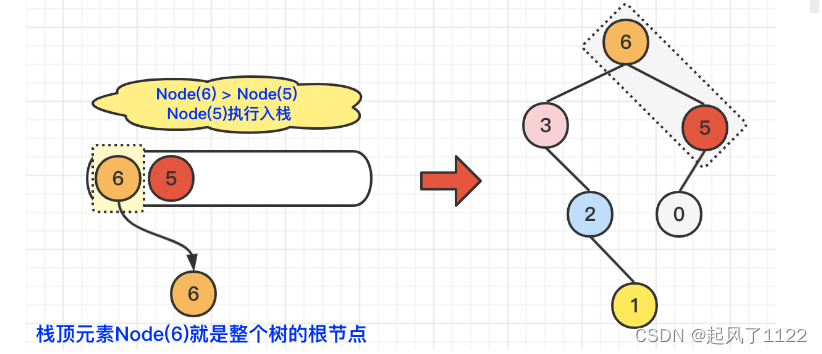
leecode654——最大二叉树
leecode最大二叉树 🌻题目要求: 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建: 创建一个根节点,其值为 nums 中的最大值。 递归地在最大值 左边 的 子数组前缀上 构建左子树。 递归地在最大值 右边 的…...

【笔试强训选择题】Day12.习题(错题)解析
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:笔试强训选择题 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!! 文章目录…...

边缘计算与开放源代码的完美结合
随着人工智能、大数据和物联网等技术的快速发展,边缘计算已经成为一种普遍使用的计算方式,尤其是在物联网领域。与此同时,越来越多的开放源代码项目也在不断涌现,这些项目为边缘计算提供了更多的选择和灵活性。那么,边…...

边缘计算网关在储能系统中的应用——提高储能系统的安全性和稳定性
随着全球能源消耗和环境保护意识的不断提高,储能技术逐渐成为了各国电力系统中的重要一环。而作为储能技术中的关键设备之一,边缘计算网关在储能系统中的应用也越来越受到关注。本文将从边缘计算网关的定义、特点以及其在储能行业中的应用三个方面来介绍…...
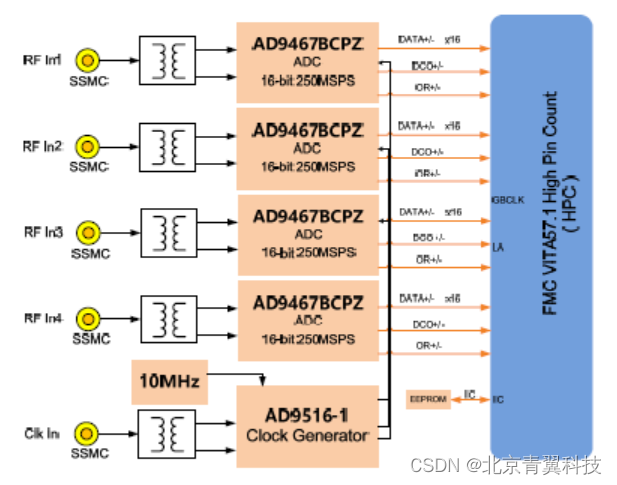
【FMC136】AD9467之4通道 250MSPS 采样率16位AD 采集子卡模块得设计原理图中文资料
板卡概述 FMC136 是一款4 通道250MHz 采样率16 位AD 采集FMC子卡,符合VITA57 规范,可以作为一个理想的IO 模块耦合至FPGA前端,4 通道AD 通过高带宽的FMC 连接器(HPC)连接至FPGA 从 而大大降低了系统信号延迟。该板卡支…...
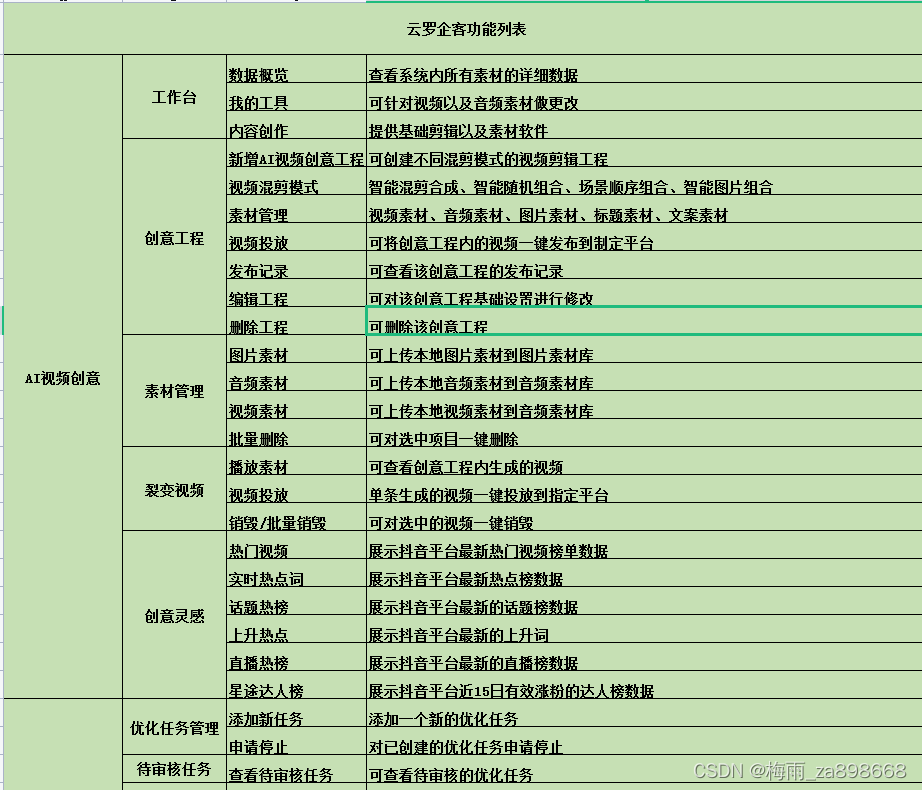
抖音SEO矩阵系统源码开发(一)
抖音seo矩阵营销系统/抖音SEO矩阵号管理系统/抖音霸屏源码开发搭建,抖音官方团队大力推广抖音SEO生态,我们应如何布局开发抖音SEO矩阵系统,来达到账号排名优化的效果,很显然,账号关键词起到了很关键的作用。首先&#…...
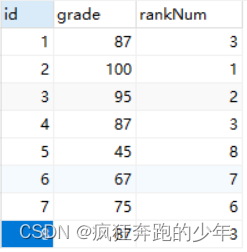
Mysql实现对某一字段排序并将排名写入另一字段
文章目录 前言一、数据库表结构和样例数据二、排名操作1.普通排名2.无间隔排名3.有间隔排名 总结 前言 最近业务上碰到这样一个需求,需要对表按照某一个字段进行排序,并且将得到的排名写入对应的排名字段。这个需求于我而言确实没有遇到过,好…...

vector容器 [上]
目录 一、 对于vector的介绍 二、vector的定义 0x01 无参构造 0x02 构造并初始化n个val 0x03 使用迭代器进行初始化构造 0x04 拷贝构造 0x05 比较 三、 vector的遍历 0x01 push_back() 0x02 operator[] 和at() 0x03 遍历 四、vector 容量空间 0x01 max_size : 返回v…...

React Native技术探究:开发高质量的跨平台移动应用的秘诀
作为一个跨平台移动应用开发框架,React Native在开发过程中能够有效提高开发效率、降低开发成本、缩短上线时间,因此备受开发者的欢迎。然而,如何使用React Native开发出高质量的跨平台移动应用呢?本文将探究这个问题,…...
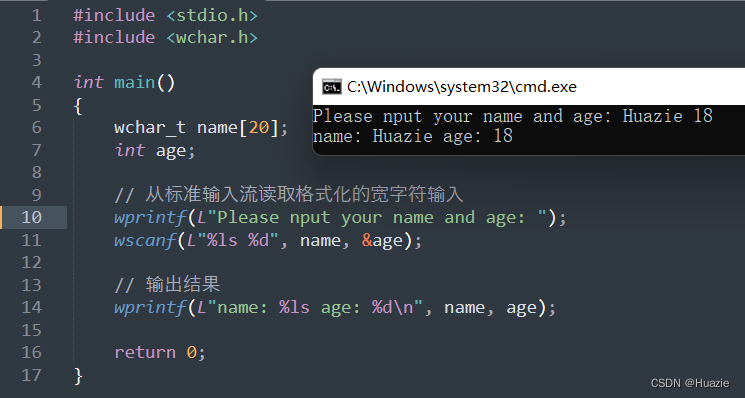
C语言函数大全-- w 开头的函数(2)
C语言函数大全 本篇介绍C语言函数大全-- w 开头的函数 1. wcstok 1.1 函数说明 函数声明函数功能wchar_t *wcstok(wchar_t *wcs, const wchar_t *delim, wchar_t **ptr);用于将一个长字符串拆分成几个短字符串(标记),并返回第一个标记的地…...

kafka启动创建topic报错:zookeeper is not a recognized option
当前使用版本:kafka_2.13-3.4.0 使用老版本的创建topic的命令,是用zookeeper来创建,但是报错如下 D:\Software\Doument\kafka_2.13-3.4.0> .\bin\windows\kafka-topics.bat --create --zookeeper localhost:2181 --replication-factor 1 …...

11个超好用的SVG编辑工具
SVG的优势在于SVG图像可以更加灵活,自由收缩放大而不影响图片的质量,一个合适的SVG编辑工具能够让你的设计事半功倍,下面就一起来看看这些冷门软件好用在哪里。这11个超好用的SVG编辑工具依次为:即时设计、Justinmind、Sketsa SVG…...
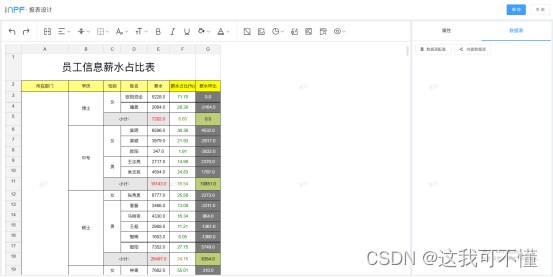
低代码平台:10分钟从入门到原理
导航目录 一、低代码概念 二、优势及局限 三、基础功能及搭建 1、业务流程 2、用户权限 3、统计图表 四、使用感受 五、总结 传统的软件研发方式目前并不能很好地满足企业的需求:人员成本高、研发时间长、运维复杂。这时低代码工具的出现为快速开发软件提供…...

【JavaScript】如何获取客户端IP地址?
使用这个库:request-ip 它按照如下顺序获取请求的IP地址: X-Client-IPX-Forwarded-For (Header may return multiple IP addresses in the format: “client IP, proxy 1 IP, proxy 2 IP”, so we take the first one.)CF-Connecting-IP (Cloudflare)F…...
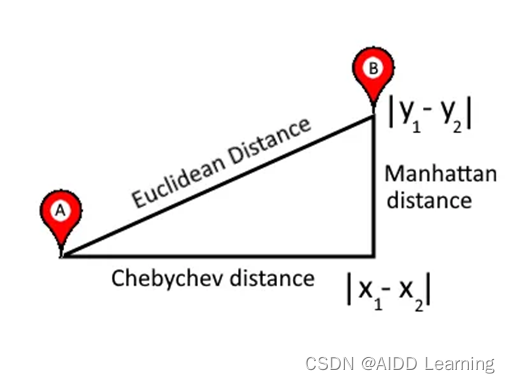
数据科学中使用的17 种相似性和相异性度量之欧氏距离
目录 1简介 2距离函数 2.1 L2范数(欧氏距离) 1简介 在数据科学中,相似性度量是一种衡量数据样本如何相互关联或相互接近的方法。另一方面,相异性度量是告诉数据对象有多少是不同的。此外,当相似的数据样本被分组到一…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
