P9234 [蓝桥杯 2023 省 A] 买瓜 题解
题目传送门
前言
说实话这题根本用不到什么折半……,今天看机房大佬写了半天加了一堆剪枝还以为很难,其实是你们想复杂了
20分钟不到从看题到代码实现
这题其实只需要可行性剪枝加排序 哦还有个后缀和
进入正题
小木棍子都听说过吧 没错就是小波上课打挂那道
跟这题没多大关系,不过如果你切了小木棍,就会觉得这道题很简单
讲讲我一开始的思路
一开始因为机房大佬在各种卡常,玄学剪枝,大叫折半是个好东西,还以为是个和小木棍一样的毒瘤
讲真我不喜欢打折半
第一眼看,排序,然后和埃及分数一样根据后续的瓜全买能不能满足剪枝,然后搜索的时候加个二分寻找当前第一个切开比剩下小的值
后面发现因为数据水所以加不加二分没差多少
最后清晰的讲述一下我的思路
第一步,先将所有的元素从大到小进行排序,然后做一下后缀和(后面可行性剪枝用)
第二步,开始搜索。
搜索的时候注意顺序要从前往后搜,也就是说后面被搜到的元素不能大于前面的(这里感性理解一下,如果大的搜了搜小的,然后搜完小的又去搜大的就重复了,排序就没有意义了)
关于可行性剪枝自然就是用第一步求出的后缀和直接判断一下后面所有的瓜加起来有没有剩下需要的瓜多
然后就结束了
关于一些小技巧
可以在读入的时候就把数据乘 2 ,这样就可以用 l o n g l o n g long long longlong 存下了(机房大佬说double常数很大)
然后就是把题目看清楚,求的是 需要切开的瓜,还有如果不行要输出 − 1 -1 −1 不然你会因此 W A WA WA 一个点
Code
#include <bits/stdc++.h>
#define int long long//记得开 long long
#define ull unsigned long longconst int N = 1e6+10;
const int M = 1e4+10;
const int mod = 1e9+7;
const int INF = 0x3f3f3f3f;using namespace std;
int a[40],n,m,b[40];
bool esmite(int pos,int res){return b[pos+1] >= res;
}
int ans = INF;
int find(int x){// STL熟练的可以使用 upper_bound 或者 lower_bound 本蒟蒻这两玩意用法分不清故手写 int l = 1, r = n;while(l < r){int mid = (l+r) >> 1;if(a[mid] / 2 <= x){r = mid;}else{l = mid+1;}}return l;
}
void dfs(int num,int rest,int pos){//num 当前切开了几个瓜,rest 还剩下需要多少瓜,pos当前搜到哪个位置了,防止往前搜 if(rest == 0){//统计答案 ans = min(ans,num);return;}if(!esmite(pos,rest)) return;//可行性剪枝 for(int i = max(pos+1,find(rest));i <= n; i++){//当然这里也可以直接pos+1(说过了数据水) if(a[i] / 2 > rest) continue;dfs(num+1,rest - a[i] / 2, i);if(a[i] > rest) continue;dfs(num,rest - a[i], i);}
}
signed main(){cin >> n >> m;m *=2;//乘2小技巧 for(int i = 1; i <= n; i++){cin>> a[i];a[i] *= 2;}sort(a+1,a+1+n,greater<int>());//排序 for(int i = n; i > 0; i--){//后缀和 b[i] = b[i+1] + a[i];}dfs(0,m,0);if(ans == INF) cout<< -1;else cout << ans;return 0;
}后记
瓜瓜永远的神! 吃瓜教万岁!
相关文章:

P9234 [蓝桥杯 2023 省 A] 买瓜 题解
题目传送门 前言 说实话这题根本用不到什么折半……,今天看机房大佬写了半天加了一堆剪枝还以为很难,其实是你们想复杂了 20分钟不到从看题到代码实现 这题其实只需要可行性剪枝加排序 哦还有个后缀和 进入正题 小木棍子都听说过吧 没错就是小波上…...
ThingsBoard自定义分发节点duplicate to related
------------------------------------内容仅博主所有,订阅者请勿泄露,感谢--------------------- 1、概述 大家好,我又更新干货了,还是那句话,我绝不像某些博主“拿我格子衫”分享那些照抄官网翻译的东西来骗订阅,我觉得那是浪费时间,要搞就搞干货,今天给大家分享Th…...

vim自动更新ctags与taglist
vim的 ctags 和 taglist 在默认情况下是不进行自动更新的,这对于编写代码是非常不方便的,好在vim的脚本还是很强大的,于是在vimrc中添加如下函数: function! UpdateCtags()let curdirgetcwd()while !filereadable("./tags&qu…...

linux查看日志常用命令,动态日志命令
linux查看日志命令,动态日志命令: tail: -n是显示行号;相当于nl命令;例子如下: tail -100f test.log 实时监控100行日志。 tail -n 10 test.log 查询日志尾部最后10行的日志。 tail -…...
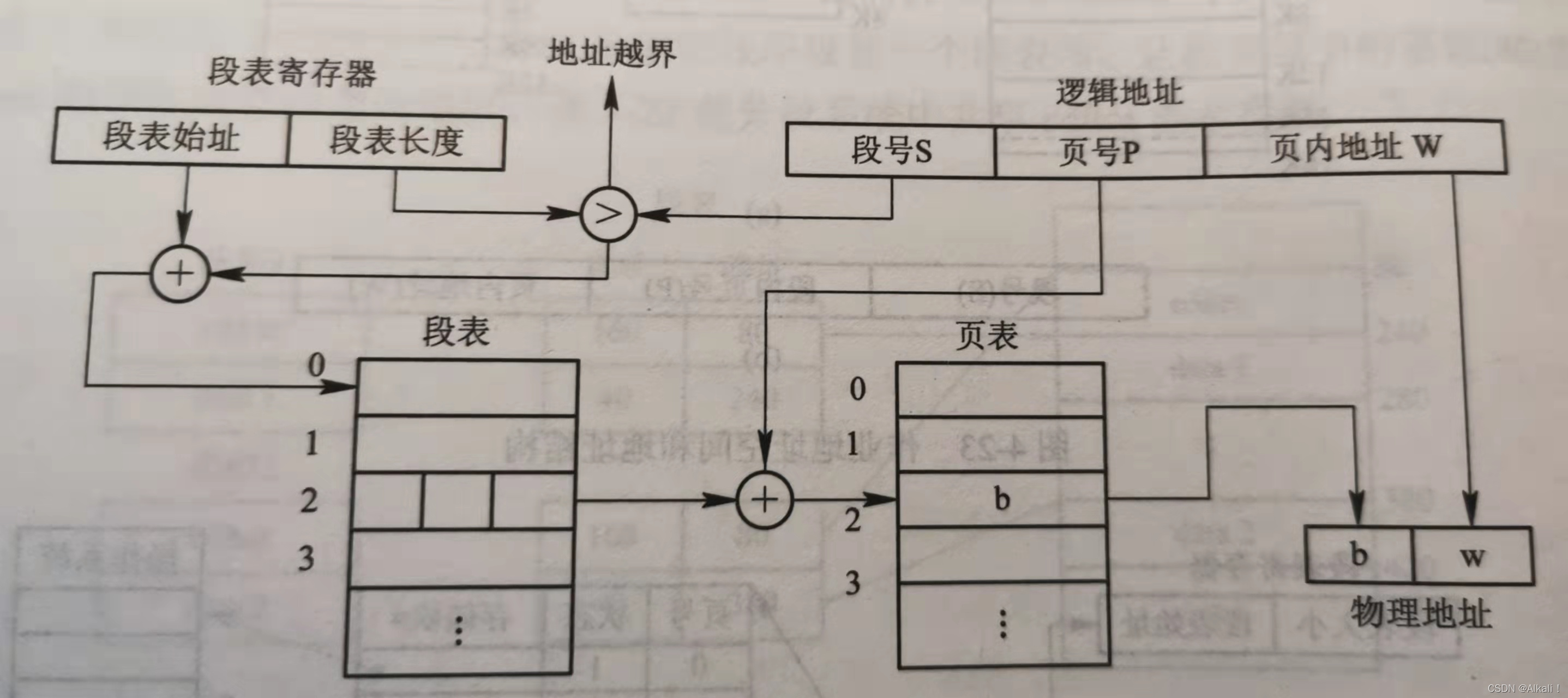
分段存储管理方式
目录 一、分段存储管理方式的引入的需求: 1.方便编程 2.信息共享 3.信息保护 4.动态增长 5.动态链接 二、分段系统的基本原理 1.分段 2.段表 3.地址变换机构 4.分页与分段的主要区别 三、信息共享 四、段页式存储管理方式 1.基本原理 2.地址变换过程 分段与分页…...
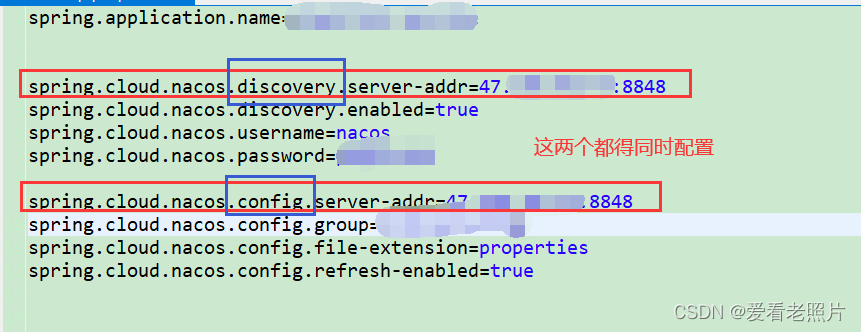
将nacos从本地切换到远程服务器上时报错:客户端端未连接,Client not connected
报错信息: 09:34:38.438 [com.alibaba.nacos.client.Worker] ERROR com.alibaba.nacos.common.remote.client - Send request fail, request ConfigBatchListenRequest{headers{charsetUTF-8, Client-AppNameunknown, Client-RequestToken65c0fbf47282ae0a7b85178…...
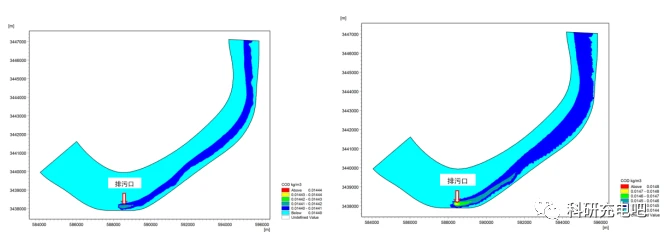
系统掌握入河排污口设置论证技术、方法及报告编制框架
在短时间内较系统的掌握入河排污口设置论证技术、方法及报告编制框架,学习内容以城镇生活污水厂、造纸项目、石化项目、制药项目案例为线索,系统讲解入河排污口设置论证报告书编制过程,并以水质模型为手段,讲解水质影响预测模型的…...

服务端渲染
服务端渲染 和 前后端分离! 渲染 什么是渲染呢 ? 其实很简单, 就是把数据反应在页面上,说白了, 就是利用 js 的语法, 把某些数据组装成 html 结构的样子, 放在页面上展示。 举个例子 : 1. 准备一段 html 结构 <h1>hello world</h1> <di…...

干货丨警惕!14个容易导致拒稿的常见错误
Hello,大家好! 这里是壹脑云科研圈,我是喵君姐姐~ 从做研究、到写论文、再到投稿,每一步都是巨大的挑战。以下列举了一些在这些过程中可能导致拒稿的常见错误,希望能帮助大家避开。 01 格式问题 1.没有遵守投稿须知 期刊提供了…...

Web基础 ( 二 ) CSS
2.CSS 2.1.概念与基础 2.1.1.什么是CSS Cascading Style Sheets 全称层叠样式单 简称样式表。 是告诉浏览器如何来显示HTML的元素的特殊标记 2.1.2.编写方式 2.1.2.1.外部文件 在html文件的<head>中加入<link>结点来引入外部的文件 <link rel"stylesh…...
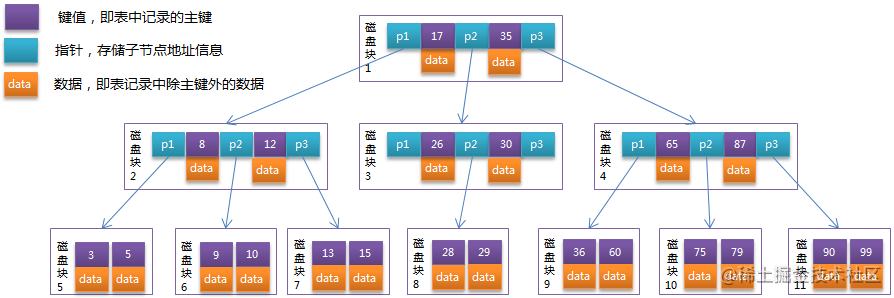
MSQL系列(一) Mysql实战-索引结构 二叉树/平衡二叉树/红黑树/BTree/B+Tree
Mysql实战-索引结构 二叉树/平衡二叉树/红黑树/BTree/BTree 我们在项目中都会使用索引,所以我们要了解索引的存储结构,今天我们就着重讲解下Mysql的索引结构存储模型,并且看下 二叉树,平衡二叉树,红黑树,B…...

理论力学专题:张量分析
张量方法的引入 自然法则与坐标无关,坐标系的引入方便分析,但也掩盖了物理本质指标符号哑标和自由标 Einstein求和约定:凡在某一项内,重复一次且仅重复一次的指标,表示对该指标在它的取值范围内求和,并称这…...

索引失效情况
左或者左右模糊匹配,like %xx,like %xx% select * from student where name like %三; 原因:B是按照索引值有序排列,只能根据前缀比较来确定数据,一旦左边是模糊的,显然无法确定到底是哪个索引值 对索引字…...
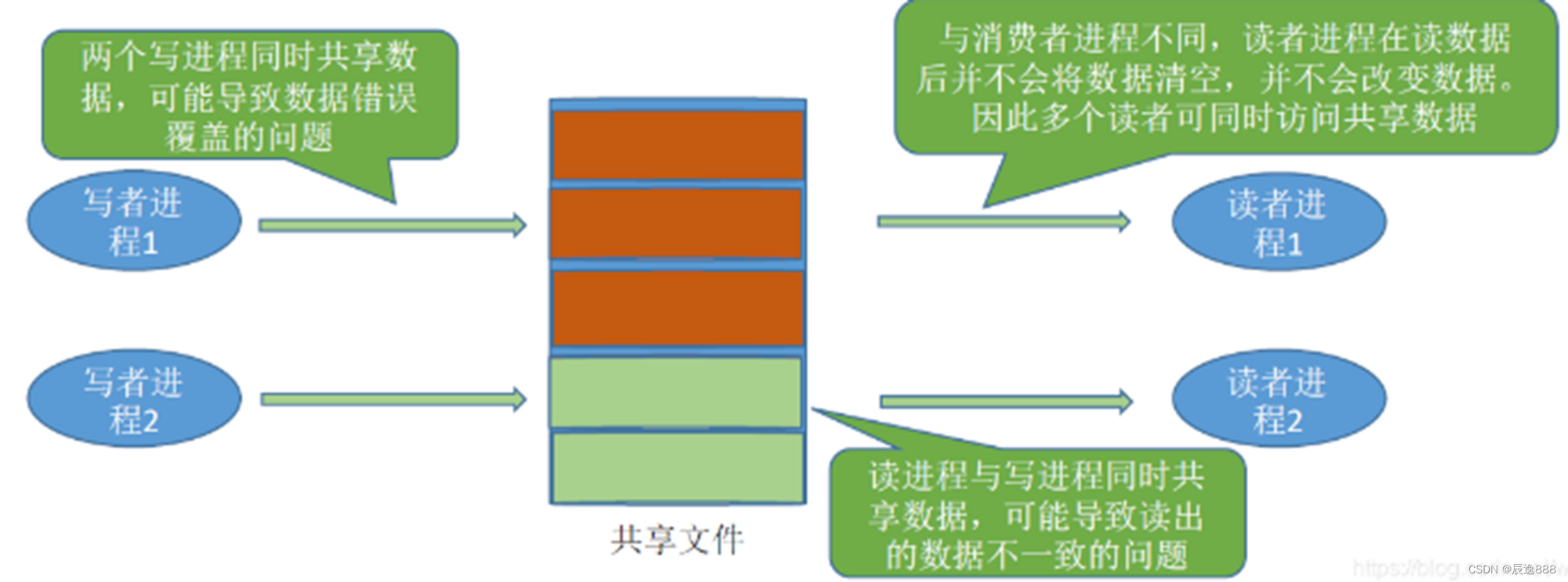
pv操作练习题
信号量解决五个哲学家吃通心面问题 题型一 有五个哲学家围坐在一圆桌旁,桌中央有盘通心面,每人面前有一只空盘于,每两人之间放一把叉子。每个哲学家思考、饥饿、然后吃通心面。为了吃面,每个哲学家必须获得两把叉子,…...

【小菜鸡刷题记】--字符串篇
【小菜鸡刷题记】:字符串 剑指 Offer 05. 替换空格剑指 Offer 58 - II.左旋转字符串剑指 Offer 20.表示数值的字符串剑指 Offer 67. 把字符串转换成整数 特此声明:题目均来自于力扣 剑指 Offer 05. 替换空格 题目链接 请实现一个函数,把字符…...
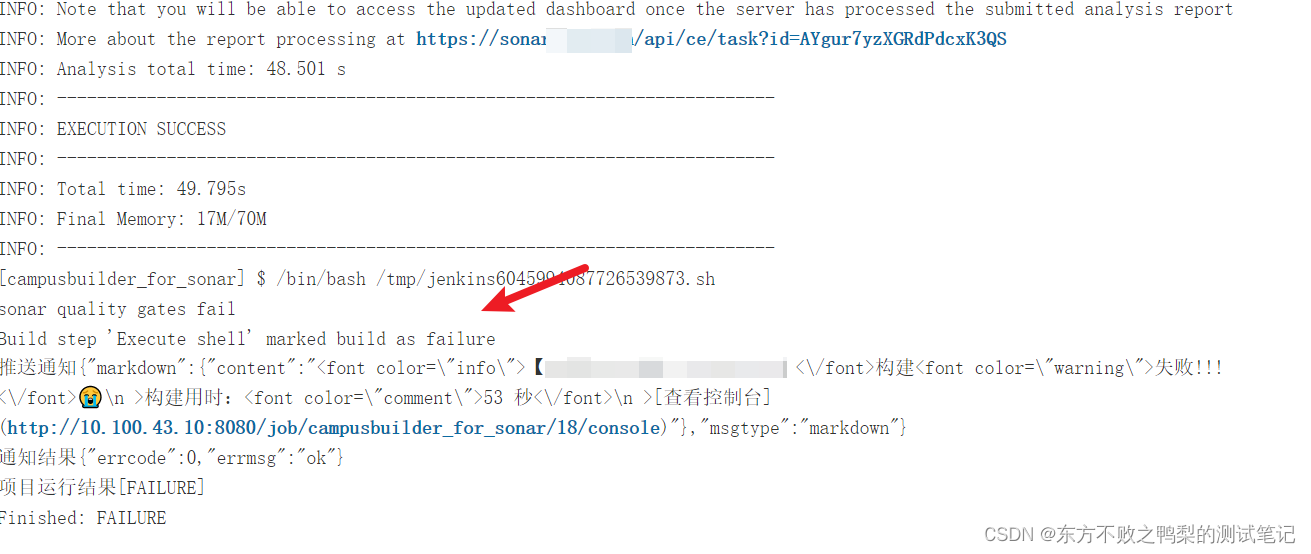
Sonar加入jenkins流水线
前提:已搭建sonarqube 1、配置sonarqube server jenkins 中manage jenkins-configure System配置sonarqube server 2、准备sonar环境 在jenkins项目的构建环境步骤中,勾选prepare SonarQube environment token需要提前在凭据里添加一个token 3、执行s…...

FSW26现金回收RS FSW43 信号和频谱分析仪
Rohde & Schwarz FSW26信号和频谱分析仪,2 Hz - 26.5 GHz 高性能 Rohde & Schwarz (R&S) FSW26 信号和频谱分析仪专为方便、准确和快速而设计。其独特的触摸屏、直观的多视图结果显示和优化的用户指南使 R&S FSW26 分析仪的操作高效方便。凭借其无…...

GraphPad Prism 9.5.1 for Mac 操作简便功能强大且实用的医学绘图分析工具
GraphPad Prism简介 GraphPad Prism是一款非常实用的统计软件,其功能非常强大,能够帮助用户进行各类科研数据的处理和分析,快速绘制出各种专业的图像和数据报告。 GraphPad Prism软件的用户界面非常友好,易于学习和操作…...

六. Activity启动模式
Task任务栈(ActivityTask) Activity属于App进程,但是Task属于操作系统,Task里面的Activity可以是属于不同的App的,所以App之间是可以相互调用的.比如:App里面可以使用打电话、地图等. 当我们查看手机后台运行的程序,他们其实就是一个个任务栈Task,我们平时可能会把他认为是一个…...
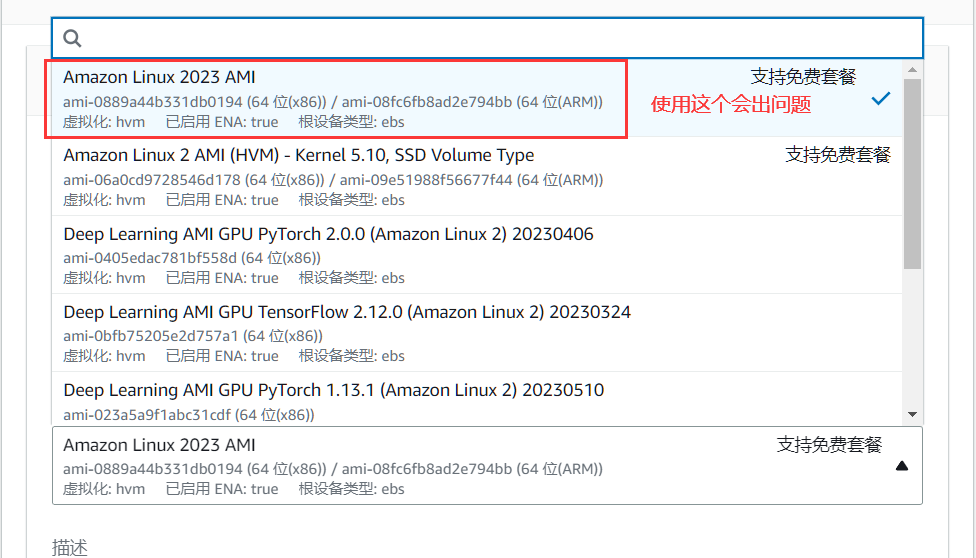
本机连接aws的ec2时报错:所选用户的用户密钥未在远程主机上注册
引言 由于工作的需要,所以需要去学习下AWS相关的知识,所以自己注册了一个AWS的账号去进行学习。 问题发现 按照启动ec2实例的步骤:选择镜像->选择系统配置->配置密钥对->配置安全组->设置存储卷大小->启动实例 在上述操作…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...
