python实现神经网络之---构建神经元模型1(python3.7)
本文主要要以周志华的机器学习书为蓝本编写
第5章神经网络
5.1python 实现神经元模型
神经网络中最基本的成分是神经元 (neuro且)模型,如下图所示:
1943 年, [McCulloch and Pitts, 1943] 将上述情形抽象为国 5.1所示的简单模型,这就是一直沿用至今的 "M-P 神经元模型 "。在这个模型中,神经元接收到来自n个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接(connection)进行传递,神经元接收到的总输入值将与神经元的阀值进行比较,然后通过"激活函数" (activation function) 处理以产生神经元的输出。
理想中的激活函数是图5.2(a)所示的阶跃函数,它将输入值映射为输出值"0"或"1",显然 "1" 对应于神经元兴奋,"0"对应于神经元抑制。然而,阶跃函数具有不连续、不光滑等不太好的性质,因此实际常用Sigmoid函数作为激活函数典型的Sigmoid函数如图5.2(b) 所示,它把可能在较大范围内变化的输入值挤压到 (0,1) 输出值范围内,因此有时也称为 "挤压函数" (squashiing function)。
把许多个这样的神经元按-定的层次结构连接起来,就得到了神经网络.事实上,从计算机科学的角度看,我们可以先不考虑神经网络是否真的模拟了生物神经网络,只需将一个神经网络视为包含了许多参数的数学模型,这个模型是若干个函数,例如的相互(嵌套)代入而得.有效的神经网络学习算法大多以数学证明为支撑。
5.1.1 Python实现Sigmoid函数
数据集如下:
计算神经元输出的方程:,
训练集输入方式:training_set_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])
训练集的输出方式:training_set_outputs = array([[0, 1, 1, 0]]).T
定Sigmoid函数:
import math
#导入math模块,然后使用math静态对象调用幂函数。
def Sigmoid(x):#定义函数y = 1 / (1 + math.exp(-x))print(y)Sigmoid(5)
相关文章:
python实现神经网络之---构建神经元模型1(python3.7)
本文主要要以周志华的机器学习书为蓝本编写 第5章神经网络 5.1python 实现神经元模型 神经网络中最基本的成分是神经元 (neuro且)模型,如下图所示: 1943 年, [McCulloch and Pitts, 1943] 将上述情形抽象为国 5.1所示的简单模型,…...
)
前端面试题 —— JavaScript (三)
一、JavaScript有哪些内置对象 全局的对象( global objects )或称标准内置对象,不要和 "全局对象(global object)" 混淆。这里说的全局的对象是说在全局作用域里的对象。全局作用域中的其他对象可以由用户的…...

【openGauss】一键编译openGauss5.0+dolphin,体验新增的mysql兼容特性
脚本 新建一个/opt/onekey-build-og.sh文件,存入以下内容 #!/bin/bash # 环境 centos 7.9 4C 8G (配置越高编译越快,4G内存编译不了,磁盘大概需要14GB) # 安装一些依赖 (libaio-devel如果不卸载重装,可能会找不到io_c…...
)
【LeetCode - 每日一题】1073. 负二进制数相加 (2023.05.18)
1073. 负二进制数相加 题意 基数为 -2 。实现两个 0/1 数组串的加法。 解法 这是一道模拟题。 设 arr1[i] 和 arr2[i] 是数组 arr1 和 arr2 从低到高的第 i 位数。 首先回顾普通的二进制数的相加,从低位开始计算,在计算的同时维护用一个变量 carry…...

软件上线会面临哪些缺陷?这四种你一定很熟悉
上线对任何软件产品来说都是一件大事,确保一切正常并且向用户发布高质量的软件非常重要。劣质、过早、不稳定、难以使用的产品会产生大量经济损失,也可能使用户对品牌本身失去信任。一直以来,我们都说应该测试,应该将缺陷修复到可…...

html监听界面被隐藏或显示
vue相比于小程序和uni-app 显然少了两个有点用的生命周期 onShow 应用被展示 onHide 应用被隐藏 但其实这个 要做其实也很简单 JavaScript中 有对应的visibilitychange事件可以监听 我们Html参考代码如下 <!DOCTYPE html> <html lang"en"> <head>…...

Springboot启动失败 DB连不上竟然是maven配置的问题
Springboot启动失败:Failed to instantiate [javax.sql.DataSource]。 最开始以为是DB版本后,需要升级驱动版本,但更新驱动版本还是不行,而且另外一个项目同样驱动同样配置可以启动。 后面发现代码读取不到yml文件中的配置信息。…...

P9234 [蓝桥杯 2023 省 A] 买瓜 题解
题目传送门 前言 说实话这题根本用不到什么折半……,今天看机房大佬写了半天加了一堆剪枝还以为很难,其实是你们想复杂了 20分钟不到从看题到代码实现 这题其实只需要可行性剪枝加排序 哦还有个后缀和 进入正题 小木棍子都听说过吧 没错就是小波上…...
ThingsBoard自定义分发节点duplicate to related
------------------------------------内容仅博主所有,订阅者请勿泄露,感谢--------------------- 1、概述 大家好,我又更新干货了,还是那句话,我绝不像某些博主“拿我格子衫”分享那些照抄官网翻译的东西来骗订阅,我觉得那是浪费时间,要搞就搞干货,今天给大家分享Th…...

vim自动更新ctags与taglist
vim的 ctags 和 taglist 在默认情况下是不进行自动更新的,这对于编写代码是非常不方便的,好在vim的脚本还是很强大的,于是在vimrc中添加如下函数: function! UpdateCtags()let curdirgetcwd()while !filereadable("./tags&qu…...

linux查看日志常用命令,动态日志命令
linux查看日志命令,动态日志命令: tail: -n是显示行号;相当于nl命令;例子如下: tail -100f test.log 实时监控100行日志。 tail -n 10 test.log 查询日志尾部最后10行的日志。 tail -…...
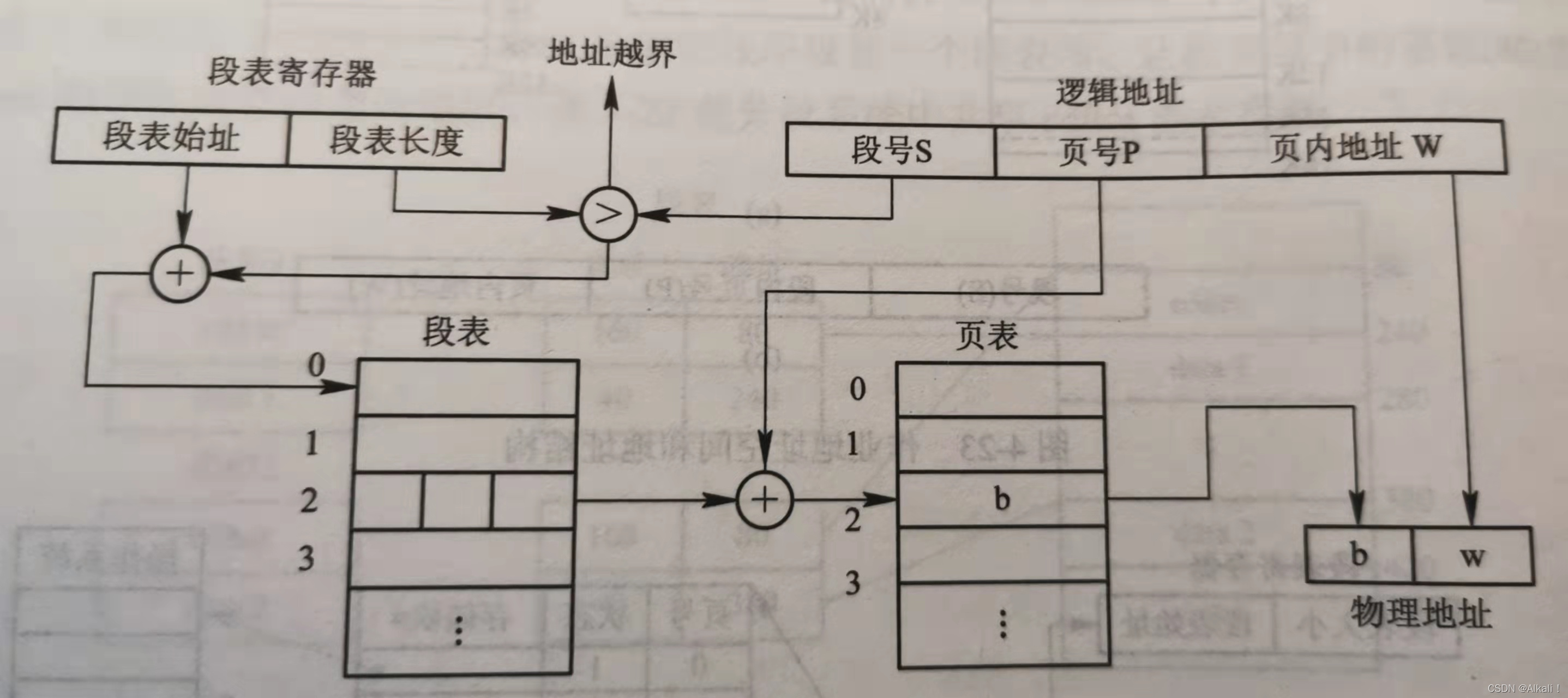
分段存储管理方式
目录 一、分段存储管理方式的引入的需求: 1.方便编程 2.信息共享 3.信息保护 4.动态增长 5.动态链接 二、分段系统的基本原理 1.分段 2.段表 3.地址变换机构 4.分页与分段的主要区别 三、信息共享 四、段页式存储管理方式 1.基本原理 2.地址变换过程 分段与分页…...
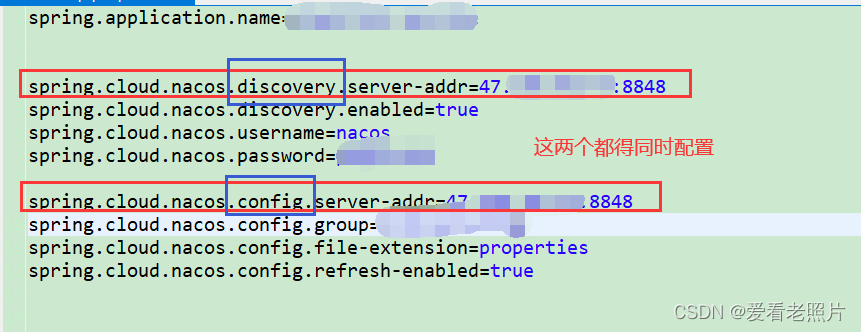
将nacos从本地切换到远程服务器上时报错:客户端端未连接,Client not connected
报错信息: 09:34:38.438 [com.alibaba.nacos.client.Worker] ERROR com.alibaba.nacos.common.remote.client - Send request fail, request ConfigBatchListenRequest{headers{charsetUTF-8, Client-AppNameunknown, Client-RequestToken65c0fbf47282ae0a7b85178…...
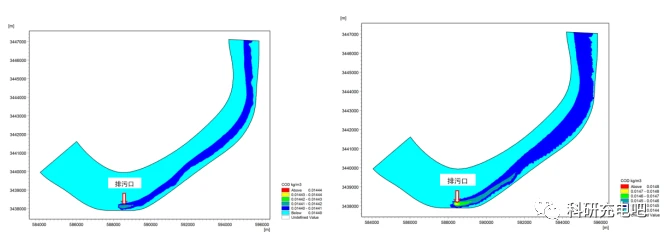
系统掌握入河排污口设置论证技术、方法及报告编制框架
在短时间内较系统的掌握入河排污口设置论证技术、方法及报告编制框架,学习内容以城镇生活污水厂、造纸项目、石化项目、制药项目案例为线索,系统讲解入河排污口设置论证报告书编制过程,并以水质模型为手段,讲解水质影响预测模型的…...

服务端渲染
服务端渲染 和 前后端分离! 渲染 什么是渲染呢 ? 其实很简单, 就是把数据反应在页面上,说白了, 就是利用 js 的语法, 把某些数据组装成 html 结构的样子, 放在页面上展示。 举个例子 : 1. 准备一段 html 结构 <h1>hello world</h1> <di…...

干货丨警惕!14个容易导致拒稿的常见错误
Hello,大家好! 这里是壹脑云科研圈,我是喵君姐姐~ 从做研究、到写论文、再到投稿,每一步都是巨大的挑战。以下列举了一些在这些过程中可能导致拒稿的常见错误,希望能帮助大家避开。 01 格式问题 1.没有遵守投稿须知 期刊提供了…...

Web基础 ( 二 ) CSS
2.CSS 2.1.概念与基础 2.1.1.什么是CSS Cascading Style Sheets 全称层叠样式单 简称样式表。 是告诉浏览器如何来显示HTML的元素的特殊标记 2.1.2.编写方式 2.1.2.1.外部文件 在html文件的<head>中加入<link>结点来引入外部的文件 <link rel"stylesh…...
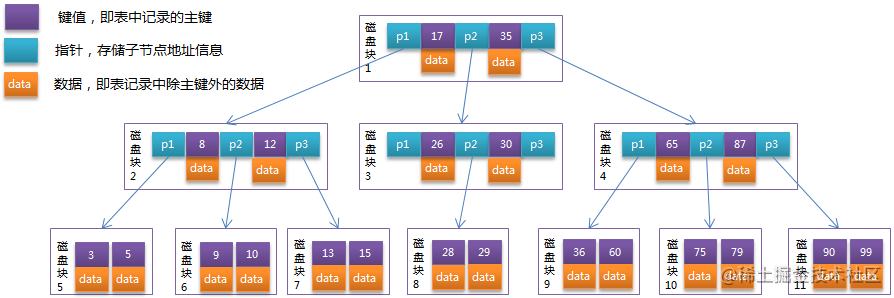
MSQL系列(一) Mysql实战-索引结构 二叉树/平衡二叉树/红黑树/BTree/B+Tree
Mysql实战-索引结构 二叉树/平衡二叉树/红黑树/BTree/BTree 我们在项目中都会使用索引,所以我们要了解索引的存储结构,今天我们就着重讲解下Mysql的索引结构存储模型,并且看下 二叉树,平衡二叉树,红黑树,B…...

理论力学专题:张量分析
张量方法的引入 自然法则与坐标无关,坐标系的引入方便分析,但也掩盖了物理本质指标符号哑标和自由标 Einstein求和约定:凡在某一项内,重复一次且仅重复一次的指标,表示对该指标在它的取值范围内求和,并称这…...

索引失效情况
左或者左右模糊匹配,like %xx,like %xx% select * from student where name like %三; 原因:B是按照索引值有序排列,只能根据前缀比较来确定数据,一旦左边是模糊的,显然无法确定到底是哪个索引值 对索引字…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...



