并行分布式计算 并行计算性能评测
文章目录
- 并行分布式计算 并行计算性能评测
- 基本性能指标
- 参数
- CPU 基本性能指标
- 存储器性能
- 并行与存储开销
- 加速比性能定律
- Amdahl 定律
- Gustafson 定律
- Sun 和 Ni 定律
- 加速比讨论
- 可括放性评测标准
- 等效率度量标准
- 等速度度量标准
- 平均延迟度量标准
- 基准评测程序(Benchmark)
并行分布式计算 并行计算性能评测
基本性能指标
参数
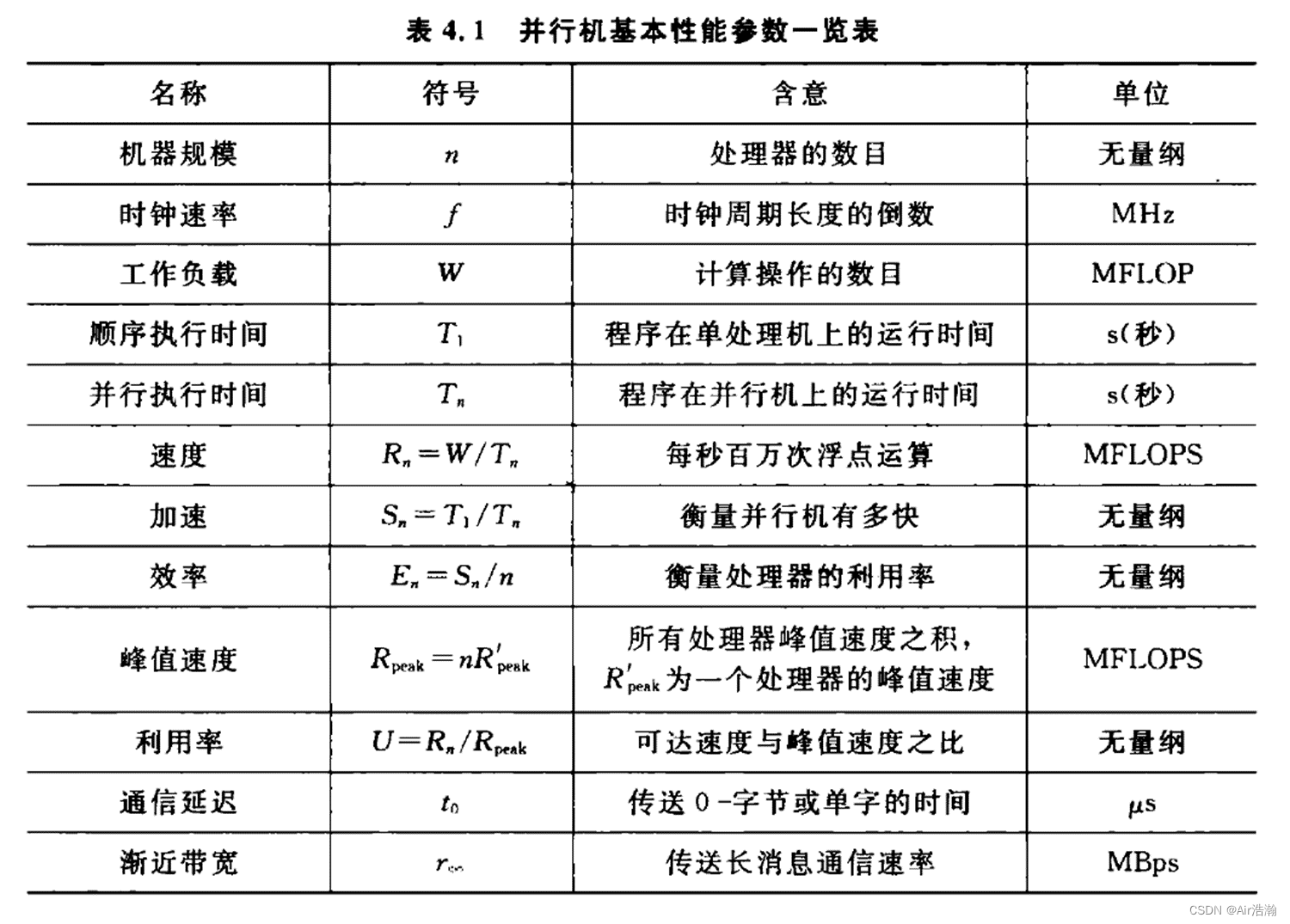
- 工作负载 W:是指某个算法的计算量;
- 加速:就是加速比;
- 峰值速度:是速度的理论上限;
CPU 基本性能指标
① 工作负载:
- 执行时间:不仅包括 CPU 时间,还包括访问存储器、磁盘时间、 I/O 时间和 OS 开销等;执行时间是不稳定的,波动较大;
- 浮点运算数(Flops):其他类型的运算可以通过经验折算成浮点运算速度;只能衡量计算任务,不能用于衡量数据传输、IO密集型的操作(虽然并行计算前期只是用于计算密集型的任务)
- 指令数目(MIPS)通常以 百万条/秒 作为单位(单条指令的执行时间差别很大)
② 无重叠的假定下并行执行时间 T n T_n Tn :
- 计算时间 T c o m p u t T_{comput} Tcomput ;并行开销时间 T p a r o T_{paro} Tparo ;相互通信时间 T c o m m T_{comm} Tcomm :
T n = T c o m p u t + T p a r o + T c o m m T_n=T_{comput}+T_{paro}+T_{comm} Tn=Tcomput+Tparo+Tcomm
- T c o m p u t T_{comput} Tcomput :与串行的时间是一致的(无重叠的假定);
- T p a r o T_{paro} Tparo :与进程管理、组操作、进程查询等相关;
- T c o m m T_{comm} Tcomm :同步(路障、锁、临界区、事件)、通信、聚合操作(规约、前缀运算),一般来说 T c o m m T_{comm} Tcomm 比 T p a r o T_{paro} Tparo 要大得多;
存储器性能
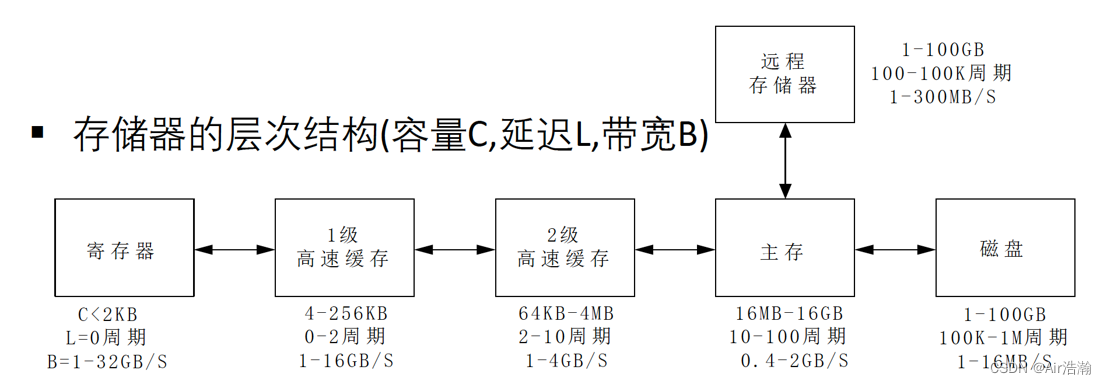
估计存储器的带宽:例如 RISC 的加法可以在单拍内完成(取出两个数相加再送回寄存器);假定字长为 8B,时钟频率 100MHZ,则带宽:
B = 3 × 8 × 100 × 1 0 6 B / s = 2.4 G B / s B=3\times8\times100\times10^6 B/s=2.4GB/s B=3×8×100×106B/s=2.4GB/s
并行与存储开销
并行和通信的开销相对于计算来说很大。
开销的测量:
- 乒乓方法(Ping-Pong Scheme):节点 - 发送 m 个字节给节点 1,节点 1 收到以后立即将消息发回节点 0,总时间除以 2;
- 热土豆法(Hot-Potato)/救火队法(Fire-Brigade):再乒乓方法的基础上,节点 1 收到以后立即发送给节点 2,直到发送给节点 n-1 后,最后发送回 0,总的时间除以 n;
点到点通信开销表达式:
t ( m ) = t 0 + m / r ∞ t(m)=t_0+m/r_{\infty} t(m)=t0+m/r∞
-
m m m :消息长度(字节数);
-
t 0 t_0 t0 :通信启动时间;
-
r ∞ r_{\infty} r∞ :渐进带宽,传送无限长消息时的通信频率;查利芳等网络结构就是为了增大渐进带宽;
-
半峰值长度 m 1 2 m_{\frac{1}{2}} m21 :达到一半渐进带宽所需要的消息长度;
-
特定性能 π 0 \pi_0 π0 :表示短消息带宽;
-
t 0 = m 1 2 / r ∞ = 1 / π 0 t_0=m_{\frac{1}{2}}/r_{\infty}=1/\pi_0 t0=m21/r∞=1/π0 ; t 0 t_0 t0 就好像是发送一个很小的包时所需要花费的时间;
典型整体通信:
- 广播(Broadcasting):处理器 0 发送 m 个字节给所有的 n 个处理器;
- 收集(Gather):处理器 0 接收所有 n 个处理器发送来的消息,最终接收 mn 个字节;尽量不要出现收集的情况,否则带宽会被 n 个处理器瓜分;
- 散射(Scatter):处理器 0 发送了 m 个字节的不同消息给所有 n 个处理器;
- 全交换(Total Exchange):每个处理器均彼此相互发送 m 个字节的不同消息给对方,总通信量为 m n 2 mn^2 mn2 个字节;很多算法需要全交换,所以通行效率或者带宽会随着处理器数量上升而快速下降;
- 循环位移(Circular-shift):处理器 i 发送 m 个字节给处理器 (i + 1) % n,总通信量为 mn 个字节;
机器的成本与价格:
- 机器的性价比(Performance/Cost Ratio):单位代价(通常为百万美元)所获取的性能(通常用 MIPS 或 MFLOPS 表示)
- 利用率:可达到的速度与峰值速度之比;
要想提高利用率,就要提高通讯量级;要想保持通讯硬件不变而提高通讯量级,就要优化算法。
加速比性能定律
Amdahl 定律
前提:
- 固定不变的计算机负载;
- 固定的计算负载分布在多个处理器上;
- 增加处理器加快执行速度,从而达到了加快处理速度的目的;
(总的计算量不变,并且被固定地、平均地分配给 p 个处理器)
参数:
-
P P P:处理器数;
-
W W W:问题规模(计算负载、问题的总计算量)
W = W s + W p W=W_s+W_p W=Ws+Wp- W s W_s Ws :应用程序中的串行分量, f f f 是串行分量比例( f = W s / W f=W_s/W f=Ws/W);
- W p W_p Wp :应用程序中可并行化部分;
-
T s = T 1 T_s=T_1 Ts=T1 :串行执行时间;
-
T p T_p Tp :并行执行时间;
-
S S S :加速比;
-
E E E :效率;
S = W s + W p W s + W p / p → p → ∞ 1 f S=\frac{W_s+W_p}{W_s+W_p/p} \stackrel{p\to\infty}{\to} \frac{1}{f} S=Ws+Wp/pWs+Wp→p→∞f1
特点:
-
适用于实时应用问题。当问题的计算负载或者规模固定时,必须通过增加处理器数目来降低计算时间;
-
加速比受到算法中串行工作量的限制;
-
扩展:若并行实现时还有额外开销,则:
S = W s + W p W s + W p / p + W o → p → ∞ 1 f + W o / W S=\frac{W_s+W_p}{W_s+W_p/p+W_o} \stackrel{p\to\infty}{\to} \frac{1}{f+W_o/W} S=Ws+Wp/p+WoWs+Wp→p→∞f+Wo/W1
Gustafson 定律
前提:对于很多大型计算,精度要求很高,而计算时间时固定不变的。此时为了提高精度,必须加大计算量,相应地必须增多处理器数才能维持时间不变。
(增大精度的同时 W s W_s Ws 几乎是不变的)
S ′ = W s + p W p W s + p W p / p = W s + p W p W s + W p = f + p ( 1 − f ) S'=\frac{W_s+pW_p}{W_s+pW_p/p}=\frac{W_s+pW_p}{W_s+W_p}={f+p(1-f)} S′=Ws+pWp/pWs+pWp=Ws+WpWs+pWp=f+p(1−f)
考虑并行开销 W o W_o Wo :
S ′ = W s + p W p W s + p W p / p + W o = f + p ( 1 − f ) 1 + W o / W S'=\frac{W_s+pW_p}{W_s+pW_p/p+W_o}= \frac{f+p(1-f)}{1+W_o/W} S′=Ws+pWp/p+WoWs+pWp=1+Wo/Wf+p(1−f)
特点:随着处理器数目的增加,串行执行部分 f f f 不再是并行算法的瓶颈。
Sun 和 Ni 定律
前提:充分利用存储空间等计算资源,尽量增大问题规模以产生更好/更精确的解,是 Amdahl 定律和 Gustafson 定律的推广。
推导:设单机存储容量为 M M M ,其工作负载 W = f W + ( 1 − f ) W W=fW+(1-f)W W=fW+(1−f)W ;
当并行系统有 p p p 个节点时,存储容量变为 p M pM pM ,用 G ( p ) G(p) G(p) 表示系统的存储容量增大 p p p 倍时工作负载的增加量,即存储容量扩大后的工作负载为 W = f W + ( 1 − f ) G ( p ) W W=fW+(1-f)G(p)W W=fW+(1−f)G(p)W ,加速比为:
S ′ ′ = f W + ( 1 − f ) G ( p ) W f W + ( 1 − f ) G ( p ) W / p = f + ( 1 − f ) G ( p ) f + ( 1 − f ) G ( p ) / p S''=\frac{fW+(1-f)G(p)W}{fW+(1-f)G(p)W/p}=\frac{f+(1-f)G(p)}{f+(1-f)G(p)/p} S′′=fW+(1−f)G(p)W/pfW+(1−f)G(p)W=f+(1−f)G(p)/pf+(1−f)G(p)
考虑并行计算的开销 W o W_o Wo :
S ′ ′ = f W + ( 1 − f ) G ( p ) W f W + ( 1 − f ) G ( p ) W / p + W o = f + ( 1 − f ) G ( p ) f + ( 1 − f ) G ( p ) / p + W o / W S''=\frac{fW+(1-f)G(p)W}{fW+(1-f)G(p)W/p+W_o}=\frac{f+(1-f)G(p)}{f+(1-f)G(p)/p+W_o/W} S′′=fW+(1−f)G(p)W/p+WofW+(1−f)G(p)W=f+(1−f)G(p)/p+Wo/Wf+(1−f)G(p)
- 当 G ( p ) = 1 G(p)=1 G(p)=1 时,就是 Amdahl 定律,意味着节点的扩展不会带来额外开销;
- 当 G ( p ) = p G(p)=p G(p)=p 时,就是 Gustafson 定律;
- 当 G ( p ) > p G(p)>p G(p)>p 时,加速比比前面两个定律得到的加速比更大;
加速比讨论
加速比经验公式:
p log p ≤ S ≤ p \frac{p}{\log p}\leq S \leq p logpp≤S≤p
-
线性加速比:很少通信开销的矩阵相加、内积运算等;
-
p / log p p/\log p p/logp 的加速比:分治类的应用问题;
-
通信密集类的应用问题: S = 1 C ( p ) S=\frac{1}{C(p)} S=C(p)1 ,这里 C ( p ) C(p) C(p) 时 p p p 个处理器的某一通信函数;
超线性加速:特殊情况下出现,例如在不同分支上进行搜索,某个处理器搜索发现结果后结束整个任务;
绝对加速:最佳串行算法与并行算法所用时间之比;(有些算法是没法直接并行化的,因此绝对加速更合理)
相对加速:同一算法在单机和并行机的运行时间。
可括放性评测标准
可括放性(Scalability):性能随处理器数的增加而按比例提高的能力。
- 影响因素:处理器数和问题规模;串行分量;并行处理的额外开销;处理器数是否超过了算法中的并发程度;
- 增加问题规模的好处:提供较高的并发机会;overhead 增加可能慢于有效计算的增加;串行分量比例随着问题规模增大而缩小;
- 增加处理器数量会增大 overhead 并降低处理器利用率,对于一个特定的并行系统(算法或程序),它们能否有效利用不断增加的处理器的能力应是受限的,而度量这种能力就是可括放性这一指标。
等效率度量标准
参数:令 t e i t^i_e tei 和 t o i t^i_o toi 分别是并行系统上第 i i i 个处理器的有用计算时间和额外开销时间(包括通信、同步和空闲的等待时间等)
T s = T e = ∑ i = 0 p − 1 t e i T 0 = ∑ i = 0 p − 1 t o i T_s=T_e=\sum\limits_{i=0}^{p-1}t_e^i \quad\quad T_0=\sum\limits_{i=0}^{p-1}t_o^i Ts=Te=i=0∑p−1teiT0=i=0∑p−1toi
T p T_p Tp 是 p p p 个处理器系统上并行算法的运行时间,对于任意 i i i 显然有:
T p = t e i + t o i p T p = T e + T o T_p=t^i_e+t_o^i \quad\quad pT_p=T_e+T_o Tp=tei+toipTp=Te+To
问题的规模 W W W 定义为最佳串行算法所完成的计算量,则 W = T e W=T_e W=Te ,因此有:
S = T e T p = T e ( T e + T o ) / p = p 1 + T o / W E = S p = 1 1 + T o / W S=\frac{T_e}{T_p}=\frac{T_e}{(T_e+T_o)/p}=\frac{p}{1+T_o/W}\quad\quad E=\frac{S}{p}=\frac{1}{1+T_o/W} S=TpTe=(Te+To)/pTe=1+To/WpE=pS=1+To/W1
为了维持一定的效率,处理器数 p p p 增大时,开销 T o T_o To 增大,问题规模 W W W 也需要相应增大。由此定义函数 f E ( p ) fE(p) fE(p) 为问题规模 W W W 随处理器数 p p p 变化的函数,为等效率函数。
优点:简单可定量计算的、少量参数计算等效率函数
缺点:如果 T o T_o To 无法计算出的话就不能用这个方法(比如在共享存储并行机中)
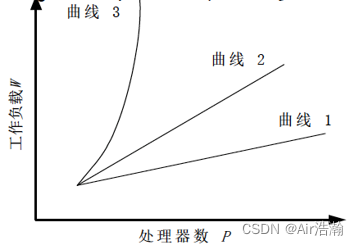
如图,3 到 1 可括放性越来越好,2 以上的表示不可扩放:
等速度度量标准
前提:在共享存储并行机中 T o T_o To 难以计算;换一种方法,如果速度能以处理器数的增加而线性增加,则说明系统具有很好的扩放性。
参数: p p p 和 W W W 前面一样, T T T 为并行执行时间,并行计算的速度 v = W / T v=W/T v=W/T ;
p p p 个处理器的并行系统的平均速度定义为并行速度除以处理器个数:
v ˉ = v p = W p T \bar{v}=\frac{v}{p}=\frac{W}{pT} vˉ=pv=pTW
令 W ′ W' W′ 表示当处理器数从 p p p 增大到 p ′ p' p′ 时,为了保持整个系统的平均速度不变所需执行的工作量,则可得到处理器数从 p p p 到 p ′ p' p′ 时平均速度可扩放度量标准公式:
Ψ ( p , p ′ ) = p ′ W p W ′ \Psi(p,\,p')=\frac{p'W}{pW'} Ψ(p,p′)=pW′p′W
Ψ ( p , p ′ ) \Psi(p,\,p') Ψ(p,p′) 介于 0 到 1 之间,越靠近 1 越好;
优点:直观使用易测量的机器性能速度指标来度量;
缺点:某些非浮点运算可能造成性能的变化没有考虑;
当 p = 1 p=1 p=1 时,有:
Ψ ( p ′ ) = Ψ ( 1 , p ′ ) = p ′ W W ′ = T 1 T p ′ = 解决工作量为 W 的问题所需串行时间 解决工作量为 W ′ 的问题所需并行时间 \Psi(p')=\Psi(1,\,p')=\frac{p'W}{W'}=\frac{T_1}{T_{p'}}=\frac{\text{解决工作量为$W$的问题所需串行时间}}{\text{解决工作量为$W'$的问题所需并行时间}} Ψ(p′)=Ψ(1,p′)=W′p′W=Tp′T1=解决工作量为W′的问题所需并行时间解决工作量为W的问题所需串行时间
区别:
- 加速比的定义是保持问题规模不变,标志对于串行系统的性能增加;
- 扩放性定义时保持平均速度不变,标志对于小系统到大规模系统所引起的性能变化;
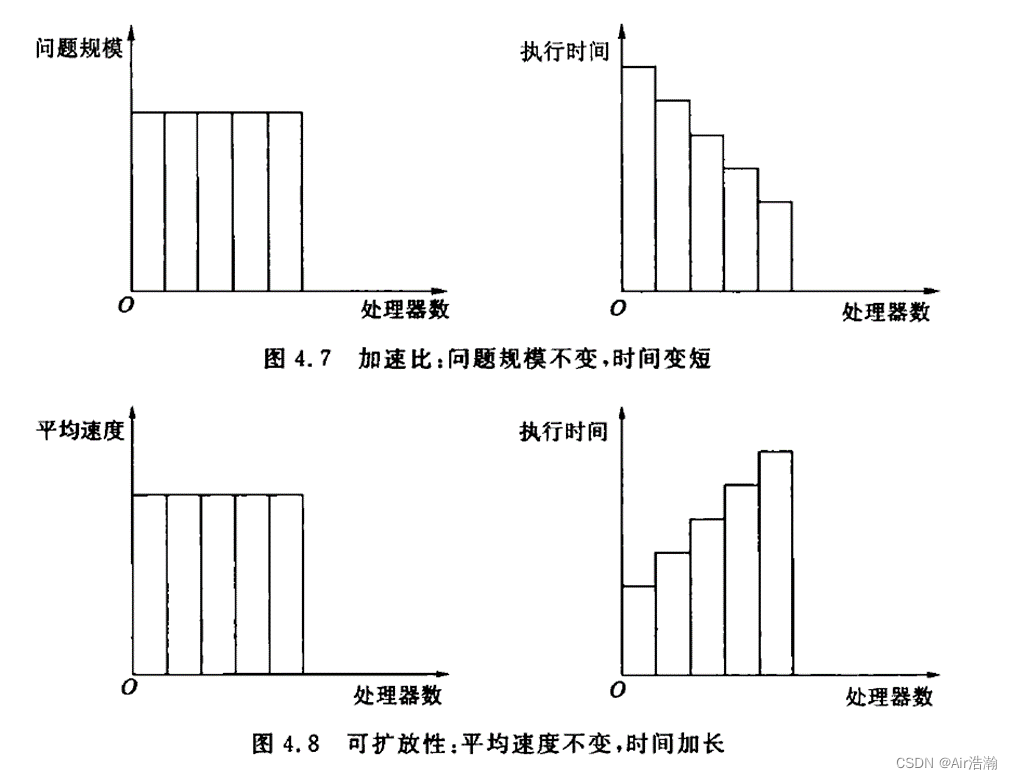
平均延迟度量标准
一个并行系统执行的时间图谱
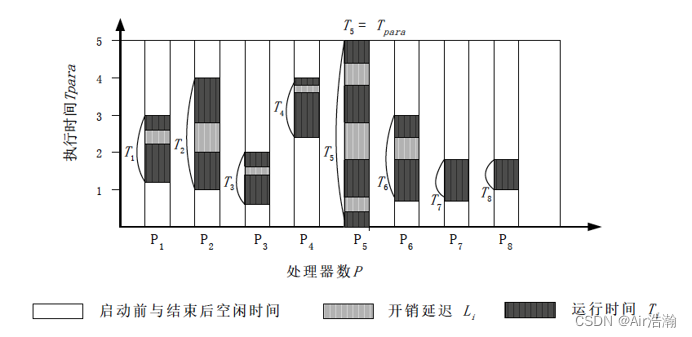
- T p a r a T_{para} Tpara 是最大的,作为总的并行时间

基准评测程序(Benchmark)
不同程序会涉及到硬件、体系结构、编译优化、编程环境、测试条件、解题算法等众多因素;根据侧重点不同,分为:
综合型:Dhrystone、Whetstone
- 缺点:对编译器比较敏感
核心型:Livermore Fortran Kernels、NASA 之 NAS
数学型:Linpack、FFT
- 常见的线性代数运算
应用型:SPEC、Perfect、Splash
并行型:NAS 之 NPB、PARKBENCH
相关文章:

并行分布式计算 并行计算性能评测
文章目录 并行分布式计算 并行计算性能评测基本性能指标参数CPU 基本性能指标存储器性能并行与存储开销 加速比性能定律Amdahl 定律Gustafson 定律Sun 和 Ni 定律加速比讨论 可括放性评测标准等效率度量标准等速度度量标准平均延迟度量标准 基准评测程序(Benchmark&…...

[网络安全]XSS之Cookie外带攻击姿势及例题详析
[网络安全]XSS之Cookie外带攻击姿势及例题详析 概念姿势及Payload启动HTTP协议 method1启动HTTP协议 method2 例题详析Payload1Payload2window.open 总结 本文仅分享XSS攻击知识,不承担任何法律责任。 本文涉及的软件等请读者自行安装,本文不再赘述。 概…...

Angular之创建项目报错:setTimeout is not defined
零基础的宝们,跟着视频学习Angular中,会教授大家如何创建一个新项目。 但是在操作时就会遇到无法创建的问题。 接下来我们一起来看看,本人Angular起步时卡在家门口的问题。 在已经安装了nodejs的情况下,被建议使用cnpm命令全局安装…...
python实现神经网络之---构建神经元模型1(python3.7)
本文主要要以周志华的机器学习书为蓝本编写 第5章神经网络 5.1python 实现神经元模型 神经网络中最基本的成分是神经元 (neuro且)模型,如下图所示: 1943 年, [McCulloch and Pitts, 1943] 将上述情形抽象为国 5.1所示的简单模型,…...
)
前端面试题 —— JavaScript (三)
一、JavaScript有哪些内置对象 全局的对象( global objects )或称标准内置对象,不要和 "全局对象(global object)" 混淆。这里说的全局的对象是说在全局作用域里的对象。全局作用域中的其他对象可以由用户的…...

【openGauss】一键编译openGauss5.0+dolphin,体验新增的mysql兼容特性
脚本 新建一个/opt/onekey-build-og.sh文件,存入以下内容 #!/bin/bash # 环境 centos 7.9 4C 8G (配置越高编译越快,4G内存编译不了,磁盘大概需要14GB) # 安装一些依赖 (libaio-devel如果不卸载重装,可能会找不到io_c…...
)
【LeetCode - 每日一题】1073. 负二进制数相加 (2023.05.18)
1073. 负二进制数相加 题意 基数为 -2 。实现两个 0/1 数组串的加法。 解法 这是一道模拟题。 设 arr1[i] 和 arr2[i] 是数组 arr1 和 arr2 从低到高的第 i 位数。 首先回顾普通的二进制数的相加,从低位开始计算,在计算的同时维护用一个变量 carry…...

软件上线会面临哪些缺陷?这四种你一定很熟悉
上线对任何软件产品来说都是一件大事,确保一切正常并且向用户发布高质量的软件非常重要。劣质、过早、不稳定、难以使用的产品会产生大量经济损失,也可能使用户对品牌本身失去信任。一直以来,我们都说应该测试,应该将缺陷修复到可…...

html监听界面被隐藏或显示
vue相比于小程序和uni-app 显然少了两个有点用的生命周期 onShow 应用被展示 onHide 应用被隐藏 但其实这个 要做其实也很简单 JavaScript中 有对应的visibilitychange事件可以监听 我们Html参考代码如下 <!DOCTYPE html> <html lang"en"> <head>…...

Springboot启动失败 DB连不上竟然是maven配置的问题
Springboot启动失败:Failed to instantiate [javax.sql.DataSource]。 最开始以为是DB版本后,需要升级驱动版本,但更新驱动版本还是不行,而且另外一个项目同样驱动同样配置可以启动。 后面发现代码读取不到yml文件中的配置信息。…...

P9234 [蓝桥杯 2023 省 A] 买瓜 题解
题目传送门 前言 说实话这题根本用不到什么折半……,今天看机房大佬写了半天加了一堆剪枝还以为很难,其实是你们想复杂了 20分钟不到从看题到代码实现 这题其实只需要可行性剪枝加排序 哦还有个后缀和 进入正题 小木棍子都听说过吧 没错就是小波上…...
ThingsBoard自定义分发节点duplicate to related
------------------------------------内容仅博主所有,订阅者请勿泄露,感谢--------------------- 1、概述 大家好,我又更新干货了,还是那句话,我绝不像某些博主“拿我格子衫”分享那些照抄官网翻译的东西来骗订阅,我觉得那是浪费时间,要搞就搞干货,今天给大家分享Th…...

vim自动更新ctags与taglist
vim的 ctags 和 taglist 在默认情况下是不进行自动更新的,这对于编写代码是非常不方便的,好在vim的脚本还是很强大的,于是在vimrc中添加如下函数: function! UpdateCtags()let curdirgetcwd()while !filereadable("./tags&qu…...

linux查看日志常用命令,动态日志命令
linux查看日志命令,动态日志命令: tail: -n是显示行号;相当于nl命令;例子如下: tail -100f test.log 实时监控100行日志。 tail -n 10 test.log 查询日志尾部最后10行的日志。 tail -…...
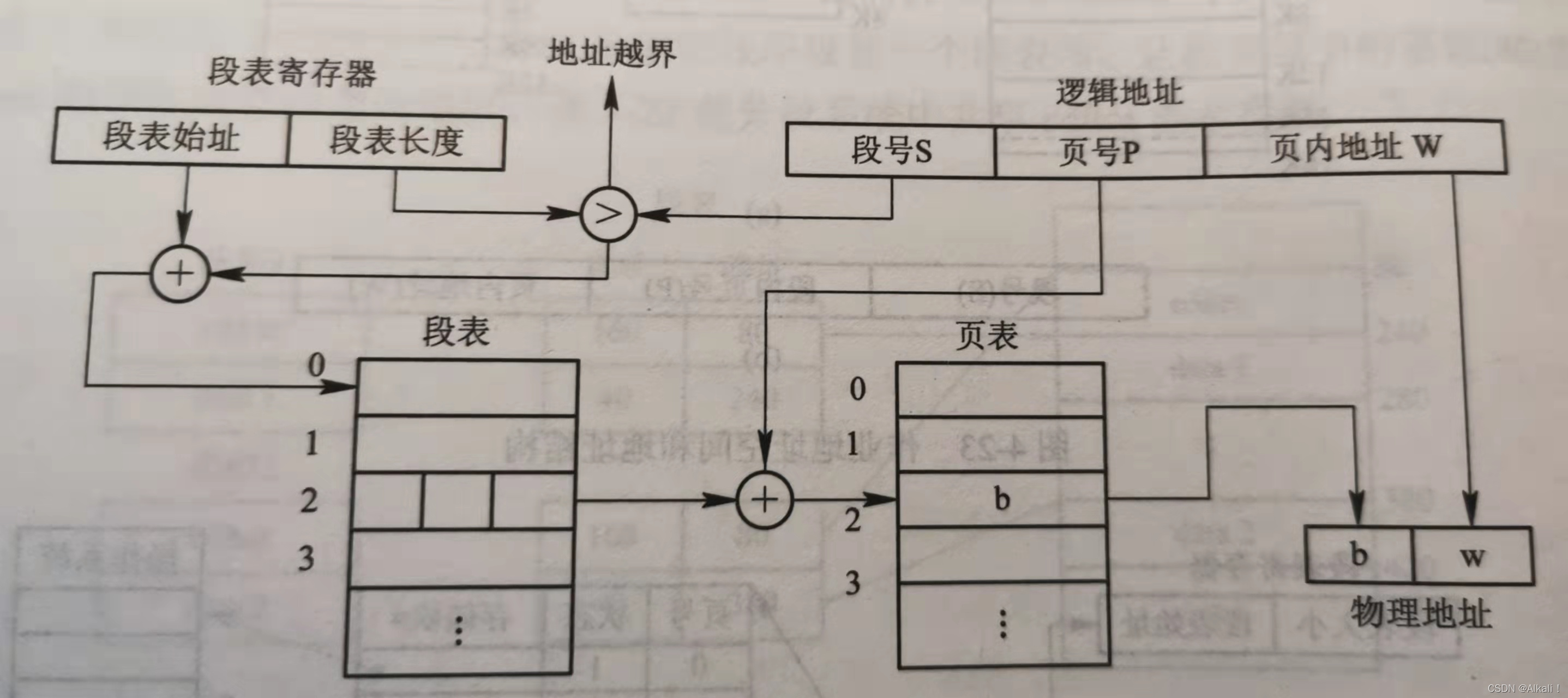
分段存储管理方式
目录 一、分段存储管理方式的引入的需求: 1.方便编程 2.信息共享 3.信息保护 4.动态增长 5.动态链接 二、分段系统的基本原理 1.分段 2.段表 3.地址变换机构 4.分页与分段的主要区别 三、信息共享 四、段页式存储管理方式 1.基本原理 2.地址变换过程 分段与分页…...
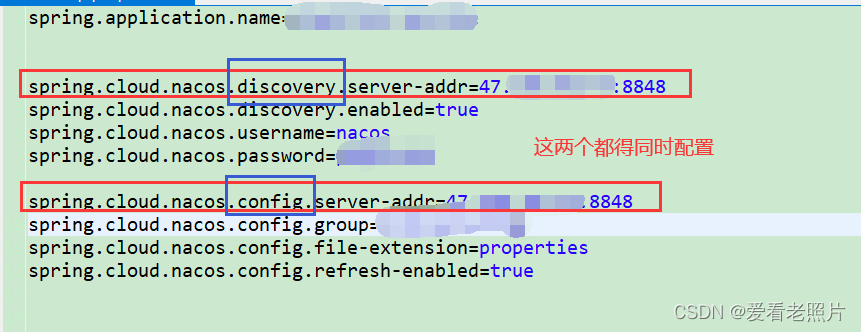
将nacos从本地切换到远程服务器上时报错:客户端端未连接,Client not connected
报错信息: 09:34:38.438 [com.alibaba.nacos.client.Worker] ERROR com.alibaba.nacos.common.remote.client - Send request fail, request ConfigBatchListenRequest{headers{charsetUTF-8, Client-AppNameunknown, Client-RequestToken65c0fbf47282ae0a7b85178…...
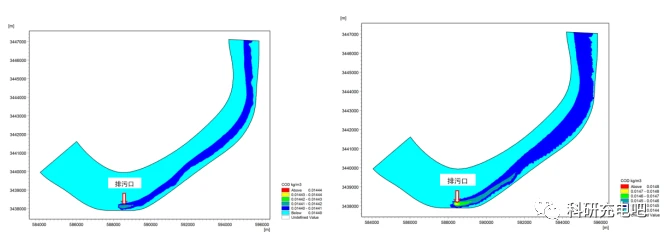
系统掌握入河排污口设置论证技术、方法及报告编制框架
在短时间内较系统的掌握入河排污口设置论证技术、方法及报告编制框架,学习内容以城镇生活污水厂、造纸项目、石化项目、制药项目案例为线索,系统讲解入河排污口设置论证报告书编制过程,并以水质模型为手段,讲解水质影响预测模型的…...

服务端渲染
服务端渲染 和 前后端分离! 渲染 什么是渲染呢 ? 其实很简单, 就是把数据反应在页面上,说白了, 就是利用 js 的语法, 把某些数据组装成 html 结构的样子, 放在页面上展示。 举个例子 : 1. 准备一段 html 结构 <h1>hello world</h1> <di…...

干货丨警惕!14个容易导致拒稿的常见错误
Hello,大家好! 这里是壹脑云科研圈,我是喵君姐姐~ 从做研究、到写论文、再到投稿,每一步都是巨大的挑战。以下列举了一些在这些过程中可能导致拒稿的常见错误,希望能帮助大家避开。 01 格式问题 1.没有遵守投稿须知 期刊提供了…...

Web基础 ( 二 ) CSS
2.CSS 2.1.概念与基础 2.1.1.什么是CSS Cascading Style Sheets 全称层叠样式单 简称样式表。 是告诉浏览器如何来显示HTML的元素的特殊标记 2.1.2.编写方式 2.1.2.1.外部文件 在html文件的<head>中加入<link>结点来引入外部的文件 <link rel"stylesh…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...
