小红的好数组陡峭值之和
题目如下

这个题我一开始是先生成满足0,1,2的全排列,但是n很大时很快就超出内存限制了,后来想到用动态规划的方法做,这里先分析一下。
n=2时,有01,02,10,12,20,21共6项,
n=3时,有010,012,020,021…共12项
容易推导出,n=m时,有3 * Math.pow(2, m-1)项
这里我们先定义一个数组f (n, i)表示第n组中以i结尾的所有数组的权值之和,比如
f(2,0)有10, 20两项,权值之和是1+2=3
f(2,1)有01,21两项,权值之和是1+1=2
同理f(2,2)=3
这几个就是我们的初始条件了
那f(n,0)怎么推到呢,0只能加在1和2的后面,如果加在1后面,如*** 10,增加的权值是1, 如果是增加在2后面,如*** 20,增加的权值是2,假设n-1组中以0结尾的数组有count个,那么增加的权值就是1 * count, 假设n-1组中以2结尾的数组有count个,那么增加的权值就是2 * count, 这里就可以写出推导式f(n,0) = f(n-1) + count * 1 + f(n-2) + 2 * count, 其他也这样推导出来。代码如下
public int fun (int m) {final int MAX = (int) Math.pow(10, 7);// 容易归纳出// n= 2时,有6个数组// n= 3时,有12个数组// n= m时,有3*math.pow(2,n-1)个数组int[][] array= new int[m+1][3]; // array[n][i]表示第n组以i结尾的数组的权值array[2][0] = 3; // 10,20array[2][1] = 2; // 01,21array[2][2] = 3; // 02,12for (int n = 3; n < m+1; n++) {int count = (int) Math.pow(2, n-2); // n-1组中分别以以0,1,2结尾的各有多少项// 第n组中以0结尾的分别是由上一组中以1和2结尾的组成// 将0添加在1后面权值+1, 共有count项,总权制增加count*1// 将0添加在2后面权值+2, 共有count项,总权制增加count*2, 其他的类推array[n][0] = (count*1 + array[n-1][1]) + (count*2 + array[n-1][2]) % MAX;array[n][1] = (count*1 + array[n-1][0]) + (count*1 + array[n-1][2]) % MAX;array[n][2] = (count*2 + array[n-1][0]) + (count*1 + array[n-1][1]) % MAX;}return (array[m][0] + array[m][1] + array[m][2]) % MAX;}相关文章:

小红的好数组陡峭值之和
题目如下 这个题我一开始是先生成满足0,1,2的全排列,但是n很大时很快就超出内存限制了,后来想到用动态规划的方法做,这里先分析一下。 n2时,有01,02,10,12,2…...

MySQL中存储具有不定列的数据-EAV模型
当需要在MySQL中存储具有不定列的数据时,一种常见的解决方案是使用EAV(Entity-Attribute-Value)模型。EAV模型允许灵活地存储不同实体的不同属性,适用于属性数量不确定的情况。本文将介绍如何使用Java和MySQL来实现EAV模型的存储和…...

COM接口规则的存在是有原因的
可能有些人认为接口上的 COM 接口规则没有必要设计的那么严格,但我想说的是,这些规则的存在是有原因的。 假设你在你的产品代码中新增加了版本号为 N 的接口,由于这个接口是内部使用的,没有任何公开文档。所以你可以随意修改它&a…...

并行分布式计算 并行计算性能评测
文章目录 并行分布式计算 并行计算性能评测基本性能指标参数CPU 基本性能指标存储器性能并行与存储开销 加速比性能定律Amdahl 定律Gustafson 定律Sun 和 Ni 定律加速比讨论 可括放性评测标准等效率度量标准等速度度量标准平均延迟度量标准 基准评测程序(Benchmark&…...

[网络安全]XSS之Cookie外带攻击姿势及例题详析
[网络安全]XSS之Cookie外带攻击姿势及例题详析 概念姿势及Payload启动HTTP协议 method1启动HTTP协议 method2 例题详析Payload1Payload2window.open 总结 本文仅分享XSS攻击知识,不承担任何法律责任。 本文涉及的软件等请读者自行安装,本文不再赘述。 概…...

Angular之创建项目报错:setTimeout is not defined
零基础的宝们,跟着视频学习Angular中,会教授大家如何创建一个新项目。 但是在操作时就会遇到无法创建的问题。 接下来我们一起来看看,本人Angular起步时卡在家门口的问题。 在已经安装了nodejs的情况下,被建议使用cnpm命令全局安装…...
python实现神经网络之---构建神经元模型1(python3.7)
本文主要要以周志华的机器学习书为蓝本编写 第5章神经网络 5.1python 实现神经元模型 神经网络中最基本的成分是神经元 (neuro且)模型,如下图所示: 1943 年, [McCulloch and Pitts, 1943] 将上述情形抽象为国 5.1所示的简单模型,…...
)
前端面试题 —— JavaScript (三)
一、JavaScript有哪些内置对象 全局的对象( global objects )或称标准内置对象,不要和 "全局对象(global object)" 混淆。这里说的全局的对象是说在全局作用域里的对象。全局作用域中的其他对象可以由用户的…...

【openGauss】一键编译openGauss5.0+dolphin,体验新增的mysql兼容特性
脚本 新建一个/opt/onekey-build-og.sh文件,存入以下内容 #!/bin/bash # 环境 centos 7.9 4C 8G (配置越高编译越快,4G内存编译不了,磁盘大概需要14GB) # 安装一些依赖 (libaio-devel如果不卸载重装,可能会找不到io_c…...
)
【LeetCode - 每日一题】1073. 负二进制数相加 (2023.05.18)
1073. 负二进制数相加 题意 基数为 -2 。实现两个 0/1 数组串的加法。 解法 这是一道模拟题。 设 arr1[i] 和 arr2[i] 是数组 arr1 和 arr2 从低到高的第 i 位数。 首先回顾普通的二进制数的相加,从低位开始计算,在计算的同时维护用一个变量 carry…...

软件上线会面临哪些缺陷?这四种你一定很熟悉
上线对任何软件产品来说都是一件大事,确保一切正常并且向用户发布高质量的软件非常重要。劣质、过早、不稳定、难以使用的产品会产生大量经济损失,也可能使用户对品牌本身失去信任。一直以来,我们都说应该测试,应该将缺陷修复到可…...

html监听界面被隐藏或显示
vue相比于小程序和uni-app 显然少了两个有点用的生命周期 onShow 应用被展示 onHide 应用被隐藏 但其实这个 要做其实也很简单 JavaScript中 有对应的visibilitychange事件可以监听 我们Html参考代码如下 <!DOCTYPE html> <html lang"en"> <head>…...

Springboot启动失败 DB连不上竟然是maven配置的问题
Springboot启动失败:Failed to instantiate [javax.sql.DataSource]。 最开始以为是DB版本后,需要升级驱动版本,但更新驱动版本还是不行,而且另外一个项目同样驱动同样配置可以启动。 后面发现代码读取不到yml文件中的配置信息。…...

P9234 [蓝桥杯 2023 省 A] 买瓜 题解
题目传送门 前言 说实话这题根本用不到什么折半……,今天看机房大佬写了半天加了一堆剪枝还以为很难,其实是你们想复杂了 20分钟不到从看题到代码实现 这题其实只需要可行性剪枝加排序 哦还有个后缀和 进入正题 小木棍子都听说过吧 没错就是小波上…...
ThingsBoard自定义分发节点duplicate to related
------------------------------------内容仅博主所有,订阅者请勿泄露,感谢--------------------- 1、概述 大家好,我又更新干货了,还是那句话,我绝不像某些博主“拿我格子衫”分享那些照抄官网翻译的东西来骗订阅,我觉得那是浪费时间,要搞就搞干货,今天给大家分享Th…...

vim自动更新ctags与taglist
vim的 ctags 和 taglist 在默认情况下是不进行自动更新的,这对于编写代码是非常不方便的,好在vim的脚本还是很强大的,于是在vimrc中添加如下函数: function! UpdateCtags()let curdirgetcwd()while !filereadable("./tags&qu…...

linux查看日志常用命令,动态日志命令
linux查看日志命令,动态日志命令: tail: -n是显示行号;相当于nl命令;例子如下: tail -100f test.log 实时监控100行日志。 tail -n 10 test.log 查询日志尾部最后10行的日志。 tail -…...
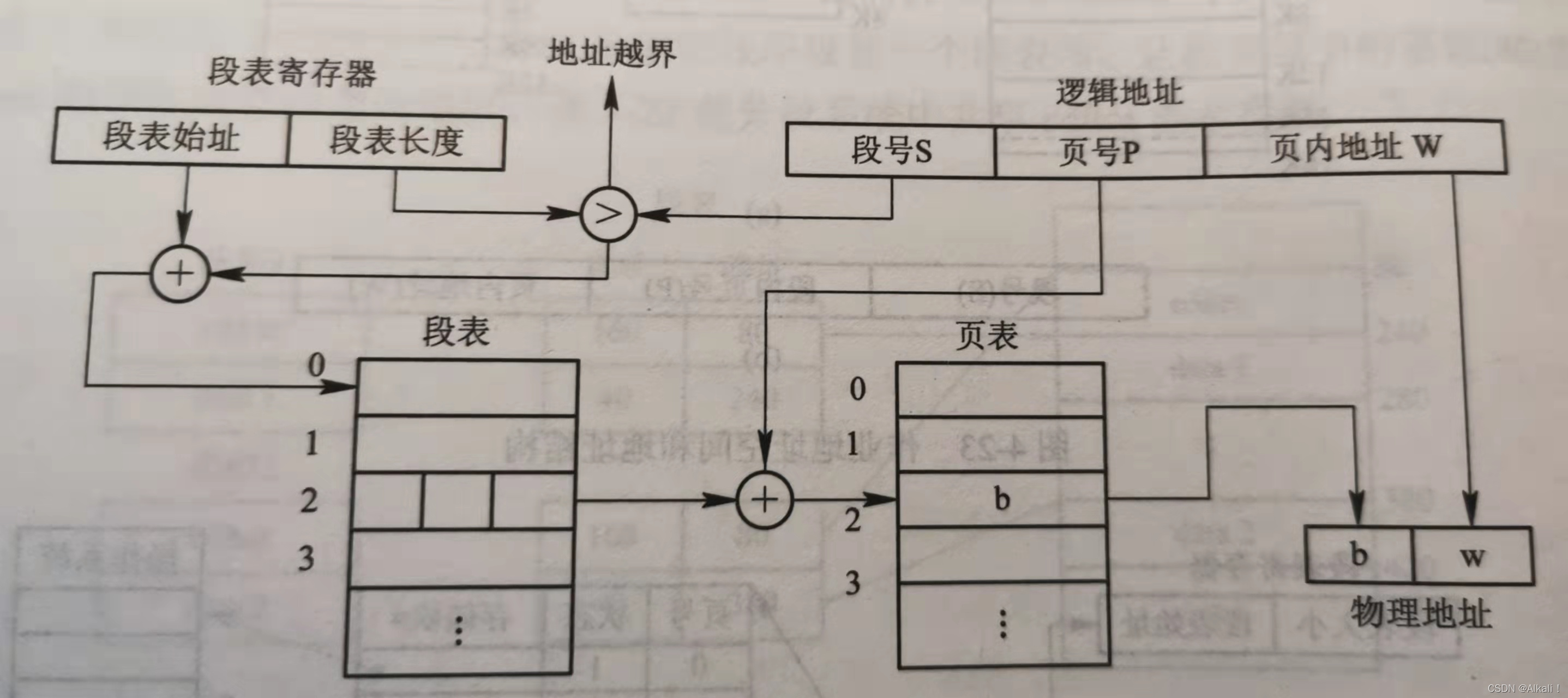
分段存储管理方式
目录 一、分段存储管理方式的引入的需求: 1.方便编程 2.信息共享 3.信息保护 4.动态增长 5.动态链接 二、分段系统的基本原理 1.分段 2.段表 3.地址变换机构 4.分页与分段的主要区别 三、信息共享 四、段页式存储管理方式 1.基本原理 2.地址变换过程 分段与分页…...
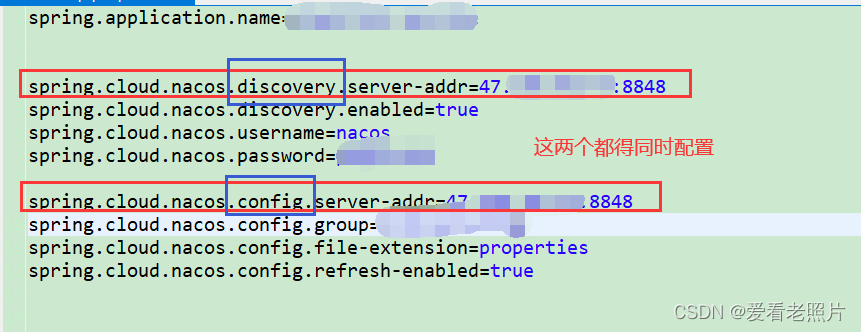
将nacos从本地切换到远程服务器上时报错:客户端端未连接,Client not connected
报错信息: 09:34:38.438 [com.alibaba.nacos.client.Worker] ERROR com.alibaba.nacos.common.remote.client - Send request fail, request ConfigBatchListenRequest{headers{charsetUTF-8, Client-AppNameunknown, Client-RequestToken65c0fbf47282ae0a7b85178…...
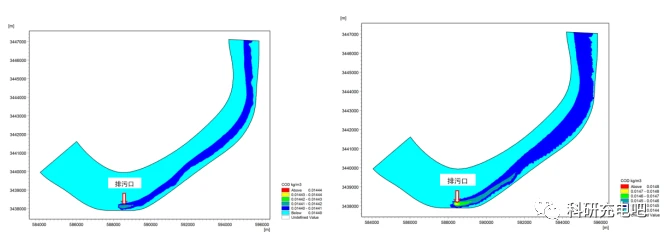
系统掌握入河排污口设置论证技术、方法及报告编制框架
在短时间内较系统的掌握入河排污口设置论证技术、方法及报告编制框架,学习内容以城镇生活污水厂、造纸项目、石化项目、制药项目案例为线索,系统讲解入河排污口设置论证报告书编制过程,并以水质模型为手段,讲解水质影响预测模型的…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
