自动控制原理笔记-根轨迹法
目录
一,根轨迹的基本概念
1.根轨迹的基本概念
2.根轨迹方程
3.根轨迹方程的应用
二,根轨迹的绘制规则
【规则一】根轨迹有n条分支:
【规则二】根轨迹对称于实轴:
【规则三】根轨迹的起点和终点:
【规则四】实轴上的根轨迹:
【规则五】根轨迹的渐近线:
【规则六】根轨迹的分离、会合点:
【规则七】出射角(起始角)和入射角(终止角):
【规则八】根轨迹与虚轴的交点:
【规则九】根之和与根之积:
小 结 :
三,系统零极点分布与响应的关系
闭环极点对系统阶跃响应的影响:
闭环零点对系统阶跃响应的影响:
闭环偶极子:
四,利用根轨迹解决工程问题
一、求控制参数(增益)的稳定边界
二、使系统具有单调过渡过程的增益范围:
三、满足调整时间要求的控制参数(增益):
四、满足超调量要求的系统增益:
五,广义根轨迹
一、参数(量)根轨迹的绘制:
二、零度根轨迹:
六,根轨迹校正
一、根轨迹的改造:
二、根轨迹校正反馈系统
一,根轨迹的基本概念
1.根轨迹的基本概念
稳定性(闭环极点位于s左半平面)快速性(动态性能:取决于闭环极点和零点)准确性(静态误差:取决于型别、开环增益和输入)
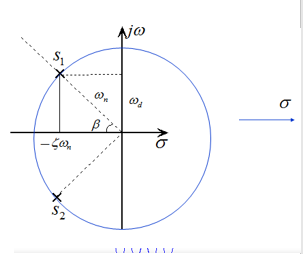
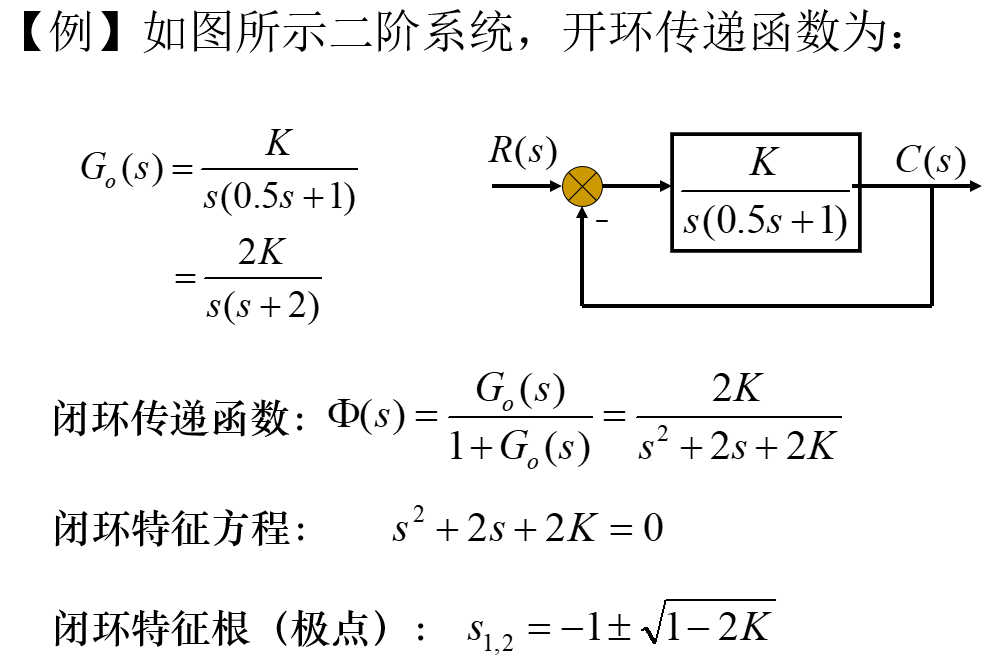

 根轨迹法的特点 : 1 )图解法,形象、直观; 2)近似方法。3)适合研究某一参数变化时系统的性能。
根轨迹法的特点 : 1 )图解法,形象、直观; 2)近似方法。3)适合研究某一参数变化时系统的性能。 2.根轨迹方程
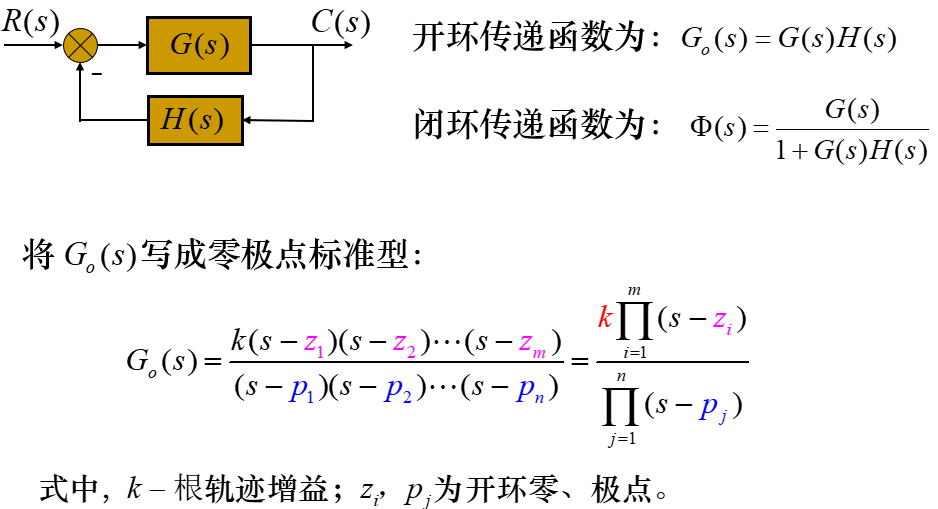

3.根轨迹方程的应用
1. 根据角条件绘制根轨迹(充要条件)

2. 根据模条件确定根轨迹增益
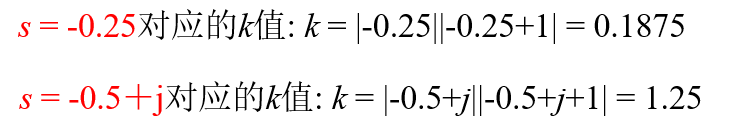
二,根轨迹的绘制规则
在根轨迹图中,“ ”表示开环极点,“ ”表示开环零点。粗实线表示根轨迹,箭头表示参数增加的方向。
【规则一】根轨迹有n条分支:
n阶实系数代数方程在复数域有n个根,因此n阶系统的根轨迹有n条分支。
【规则二】根轨迹对称于实轴:
实系数的闭环特征(代数)方程的根必对称于实轴。
【规则三】根轨迹的起点和终点:
根轨迹方程为:
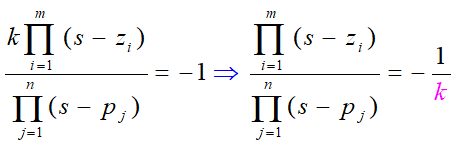

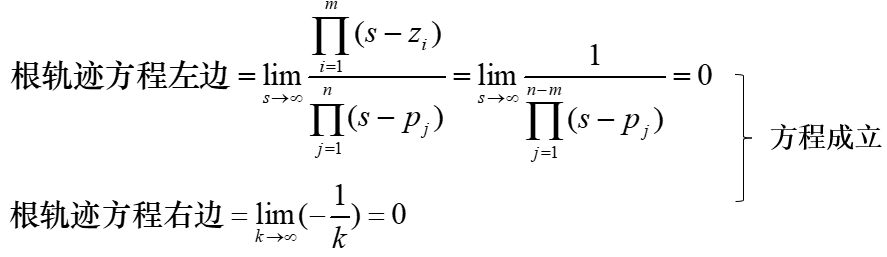
亦称系统有n-m个无限远零点。有限值零点加无穷远零点的个数等于极点数(=根轨迹条数=系统阶次n)。
【规则四】实轴上的根轨迹:
若实轴上某一线段的右边,开环零点和开环极点的数目之和为奇数(odd),则该线段为根轨迹的一部分。

若实轴上某一线段的右边,开环零点和开环极点的数目之和为奇数,则该线段为根轨迹的一部分。
【规则五】根轨迹的渐近线:
k→∞时趋向无穷远处的根轨迹共有n-m条。这n-m条根轨迹趋向无穷远的方向由渐近线决定。


【规则六】根轨迹的分离、会合点:
不同的根轨迹分支在s平面上相交的点,称为根轨迹的分离、会合点。
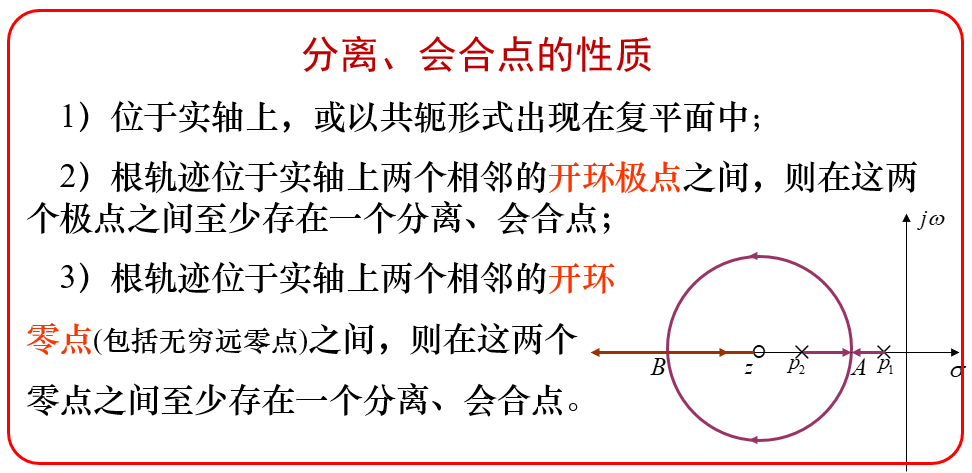
分离、会合点的求法:
①求导法:根轨迹在实轴上的分离、会合点表示这些点是闭环特征方程的重根点。
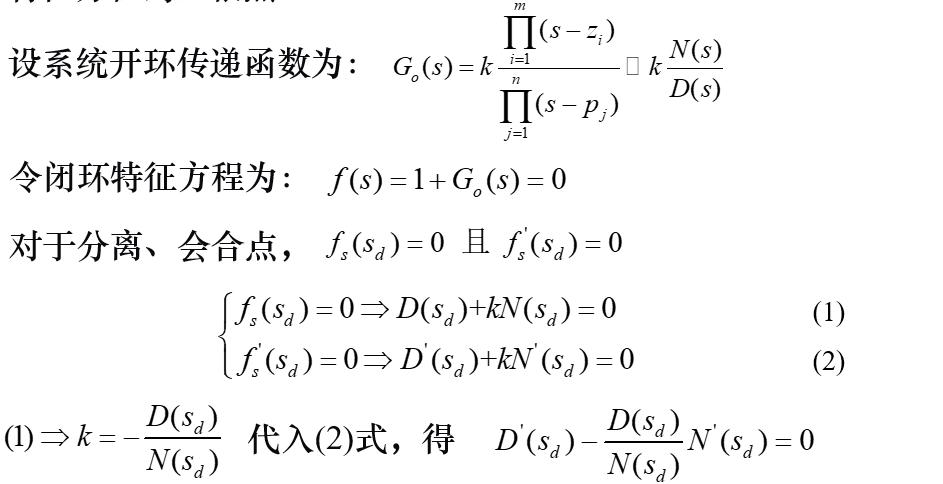
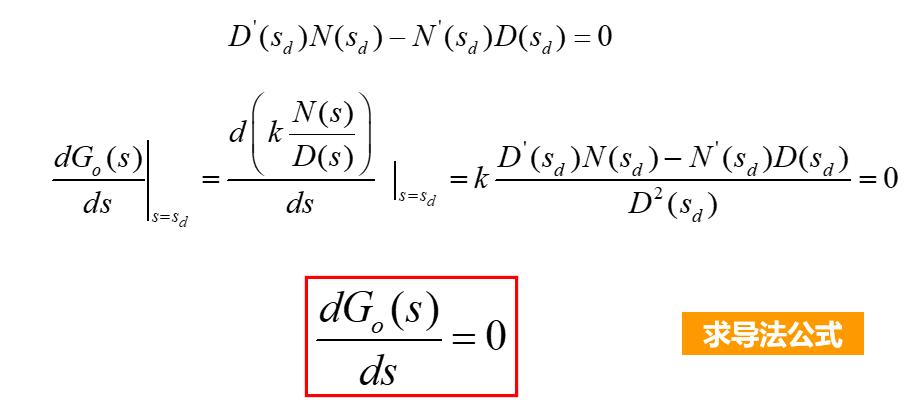
注意:由上式可求得的点是分离、会合点必要条件,还需求出这些点对应的增益,若增益为大于零的实数,则所求出的点为分离、会合点。

②工程法:



定理:当系统有2个开环极点、 1个或2个开环零点,并且在复平面上有根轨迹时,则复平面上的根轨迹一定是以零点为圆心的圆弧
【规则七】出射角(起始角)和入射角(终止角):



【规则八】根轨迹与虚轴的交点:
根轨迹和虚轴相交时,闭环特征方程有一对共轭纯虚根,系统处于临界稳定状态。这时的增益 称为临界根轨迹增益。



【规则九】根之和与根之积:



小 结 :

三,系统零极点分布与响应的关系
控制系统的闭环极点、零点与系统的稳定性及动态性能有密切关系。闭环零点与开环零点相同,闭环极点由根轨迹方程表示出来。
闭环极点对系统阶跃响应的影响:

单位阶跃响应为:
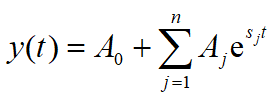
(1)稳定性:sj应位于s左半平面;
(2)快速性:极点尽可能远离虚轴;
(3)平稳性:振荡要小,接近最佳阻尼比;
(4)利用闭环主导极点进行高阶系统的近似处理;
(5)闭环零点可以削弱其附近闭环极点对系统的影响(对应的留数小)。
闭环零点对系统阶跃响应的影响:

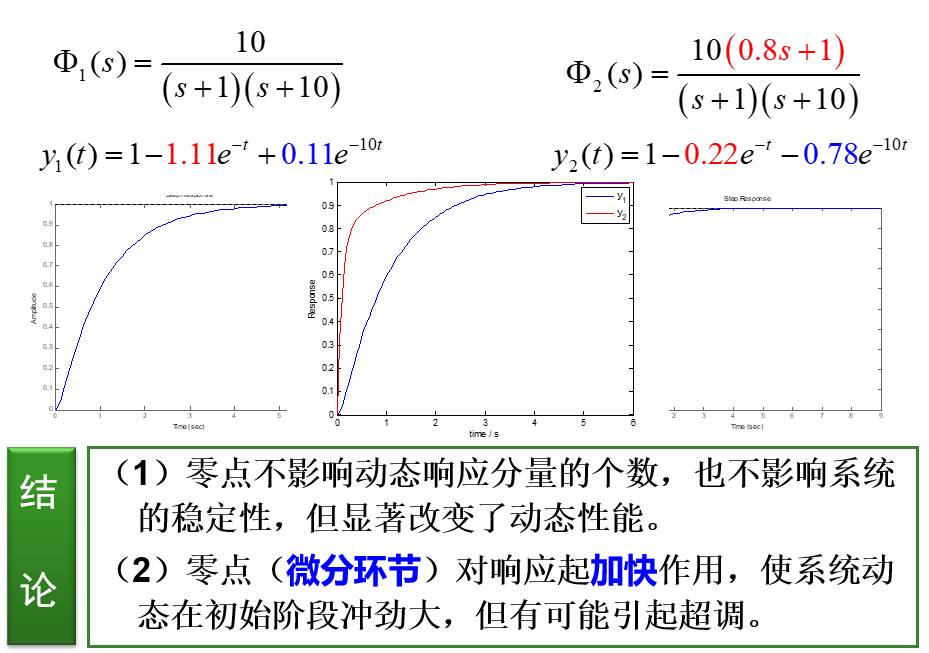
闭环偶极子:
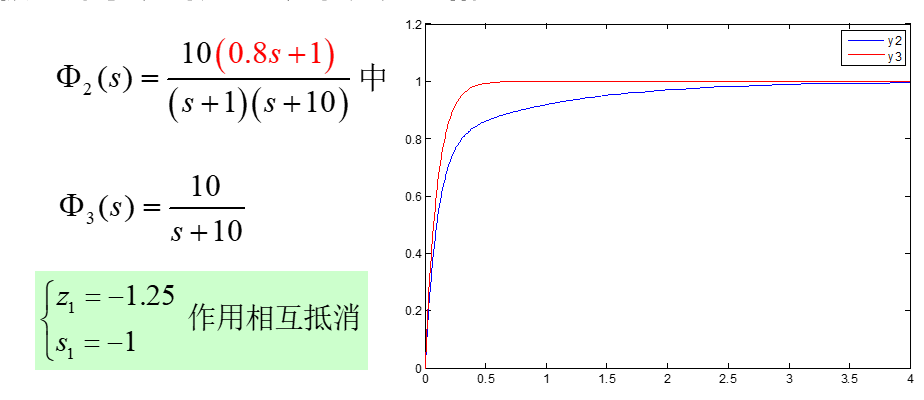
闭环偶极子:复平面上很接近的一对闭环零极点
相对于其他零极点,相互距离在1/10以下的一对闭环偶极子对系统响应的影响可以忽略。
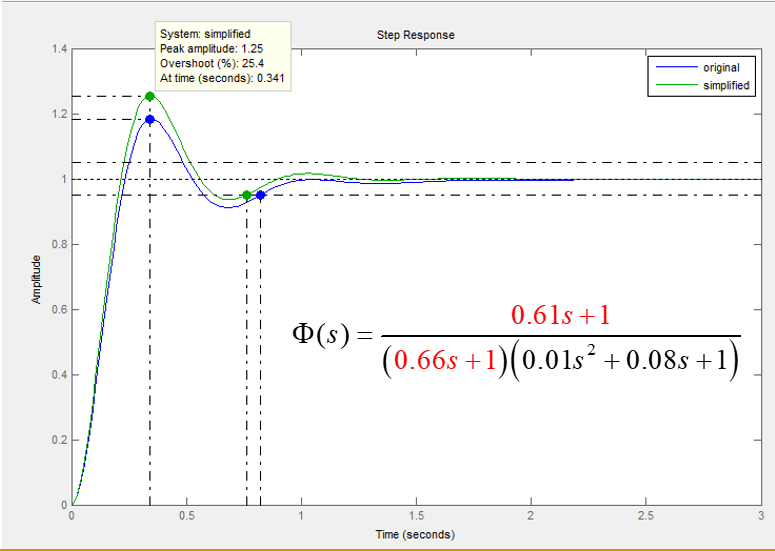
四,利用根轨迹解决工程问题
一、求控制参数(增益)的稳定边界
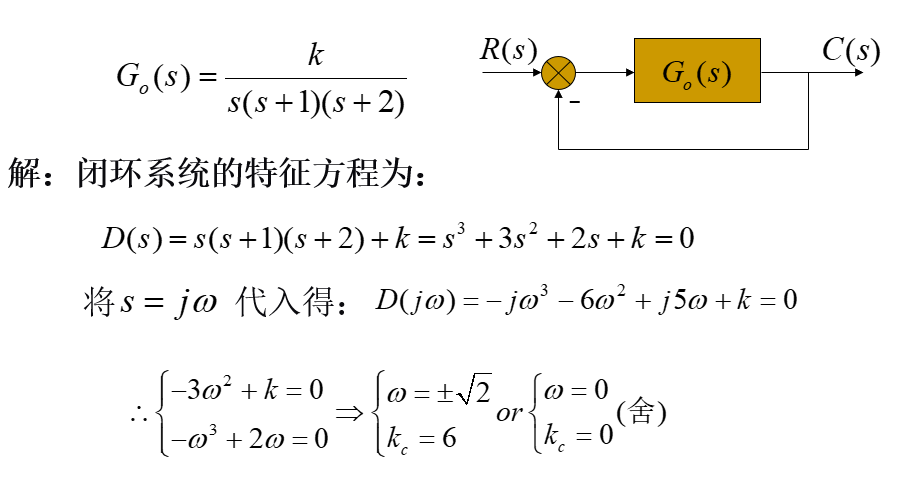
二、使系统具有单调过渡过程的增益范围:

三、满足调整时间要求的控制参数(增益):

四、满足超调量要求的系统增益:
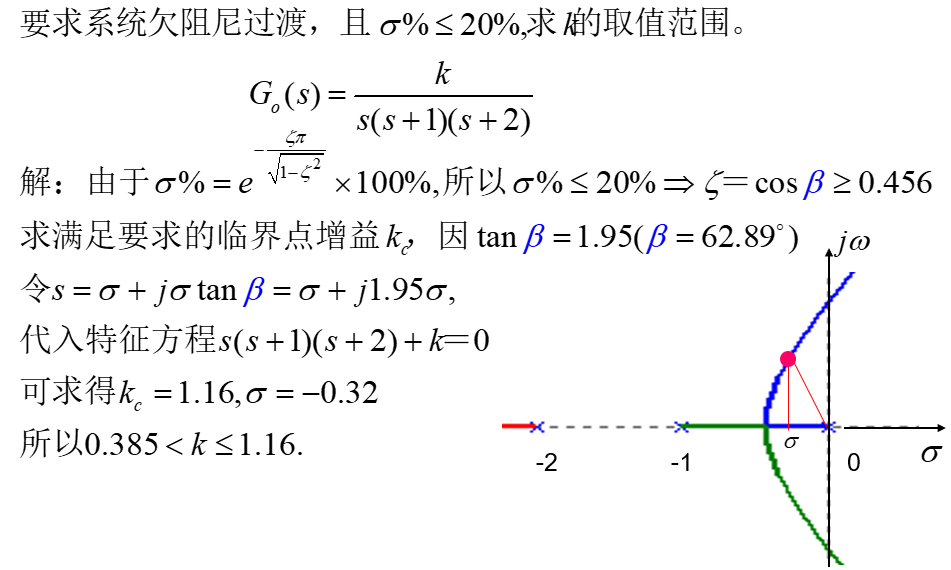
利用根轨迹解决工程问题,实际上是根据系统性能指标的要求,求出主导极点在s平面的分布区域
五,广义根轨迹
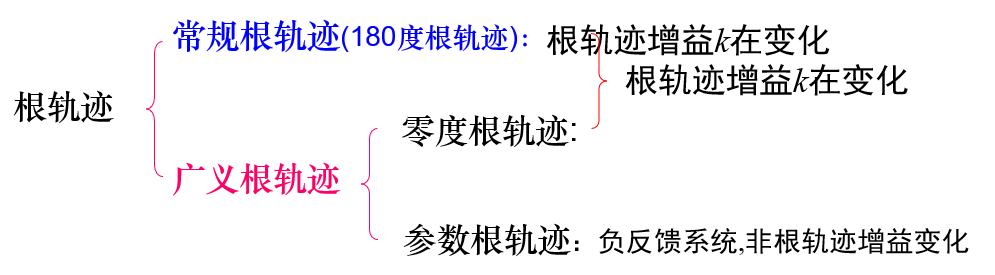
一、参数(量)根轨迹的绘制:

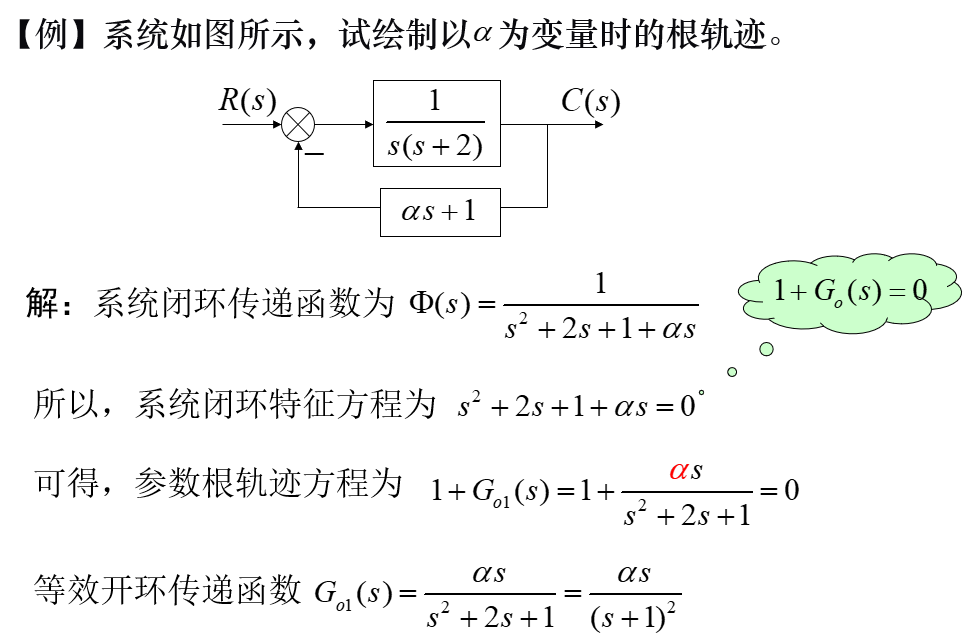
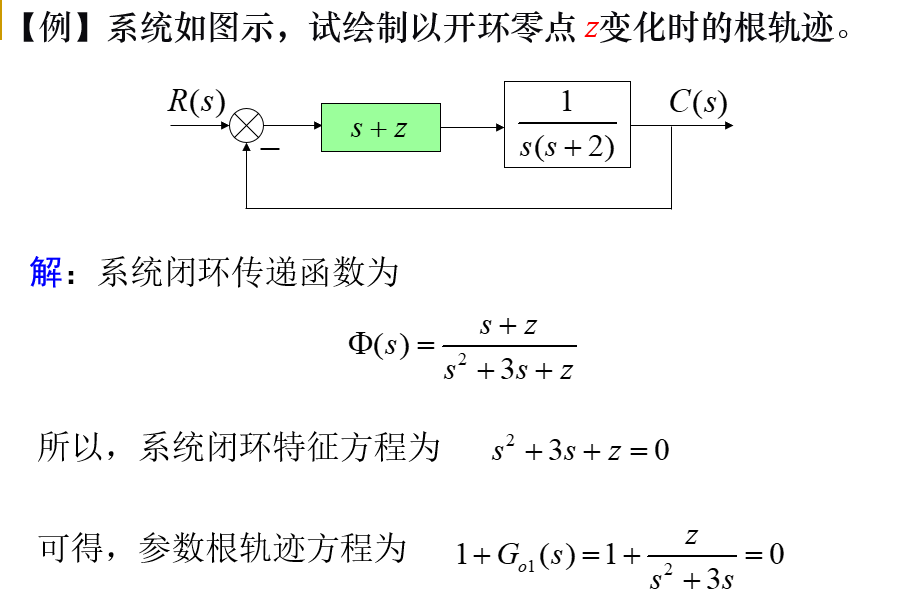
绘制参数根轨迹,需由系统的闭环特征方程导出一个新的等效开环传递函数Go1(s)。 在Go1(s)中,可变参数的位置与常规根轨迹中的根增益 k 位置相同。
二、零度根轨迹:
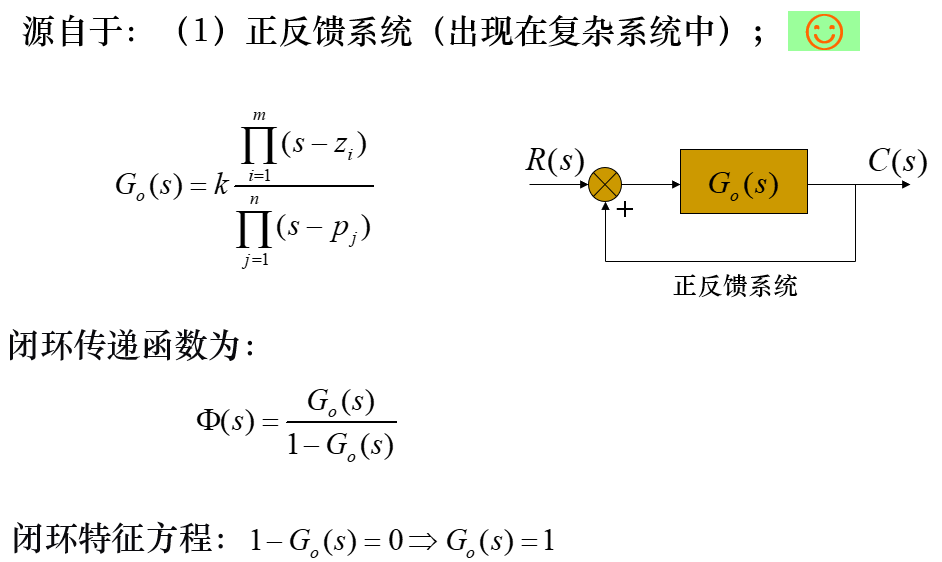

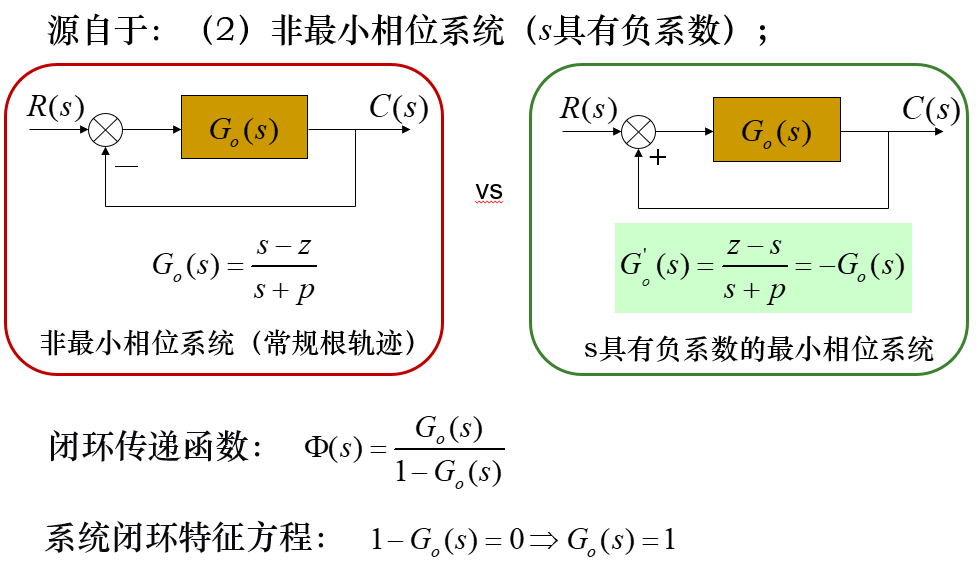

零度根轨迹的绘制规则:




六,根轨迹校正
一、根轨迹的改造:
1、增加开环零点对根轨迹的影响:
1)改变了根轨迹在实轴上的分布;
2)改变了渐近线的条数、与实轴的交点、夹角;
3)可以抵消对系统不利的闭环极点(构成偶极子);
4)根轨迹左移(零点要适当),对稳定性有利;
2、增加开环极点对根轨迹的影响
1)改变了根轨迹的条数;
2)改变了根轨迹在实轴上的分布;
3)改变了渐近线的条数、与实轴的交点、夹角;
4)根轨迹右移(极点要适当),对稳定性不利;
3、 增加开环偶极子对根轨迹的影响

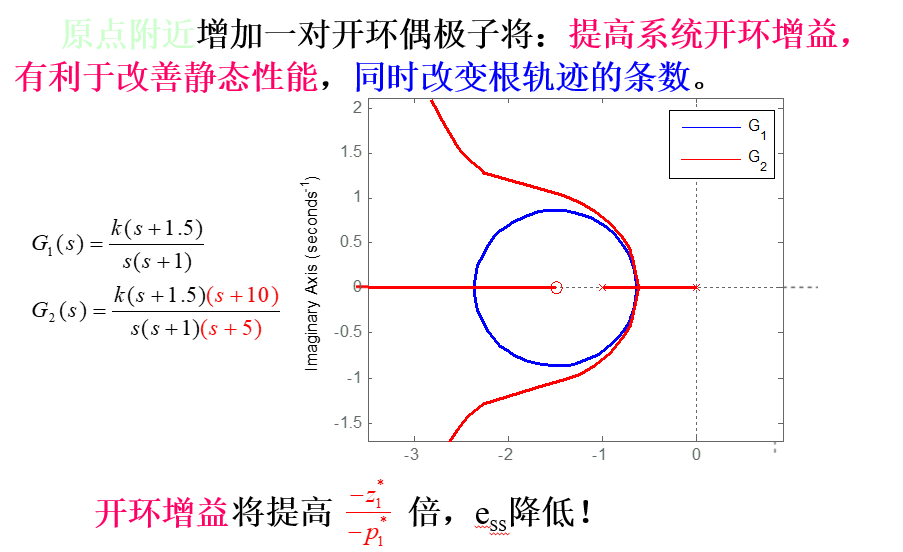
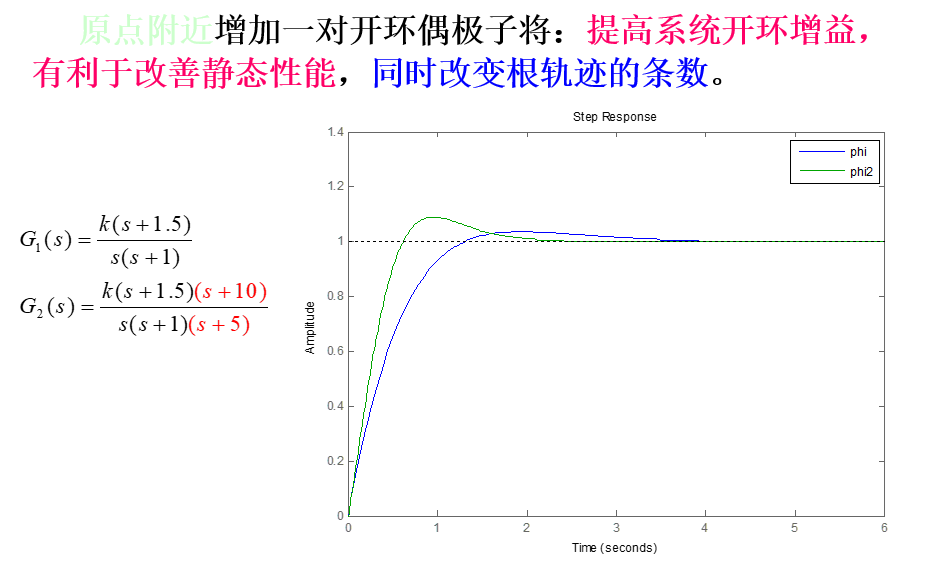

二、根轨迹校正反馈系统
step: 1)暂态性能指标→期望的闭环主导极点;
2)绘制原系统的根轨迹,确定是否增加校正装置;
3)校正后系统根轨迹通过期望闭环主导极点,检验开环比例系数是否满足静态指 标(否则,增加开环偶极子以改善之);
4)检验暂、静态指标。
相关文章:

自动控制原理笔记-根轨迹法
目录 一,根轨迹的基本概念 1.根轨迹的基本概念 2.根轨迹方程 3.根轨迹方程的应用 二,根轨迹的绘制规则 【规则一】根轨迹有n条分支: 【规则二】根轨迹对称于实轴: 【规则三】根轨迹的起点和终点: 【规则四】…...

准备半个月,面试5分钟不到就凉了,问的实在太····
从外包出来,没想到竟然死在了另一家厂子 自从加入这家公司,每天都在加班,钱倒是给的不少,所以我也就忍了。没想到12月一纸通知,所有人都不许加班,薪资直降30%,顿时有吃不起饭的赶脚。 好在有个…...
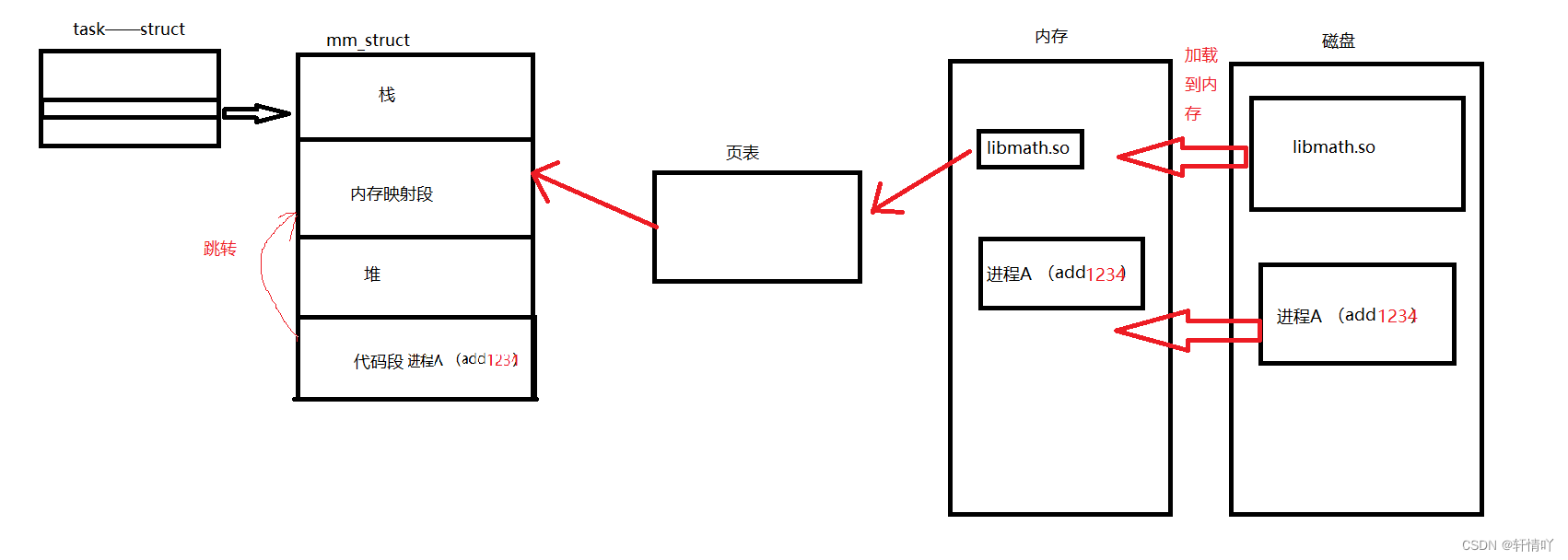
基础IO(三)
软硬链接和动静态库 1.软硬链接2.动态库和静态库2.1理解现象2.2静态库的设计2.3动态库2.4动态库的配置2.5动态库的理解 🌟🌟hello,各位读者大大们你们好呀🌟🌟 🚀🚀系列专栏:【Linux…...
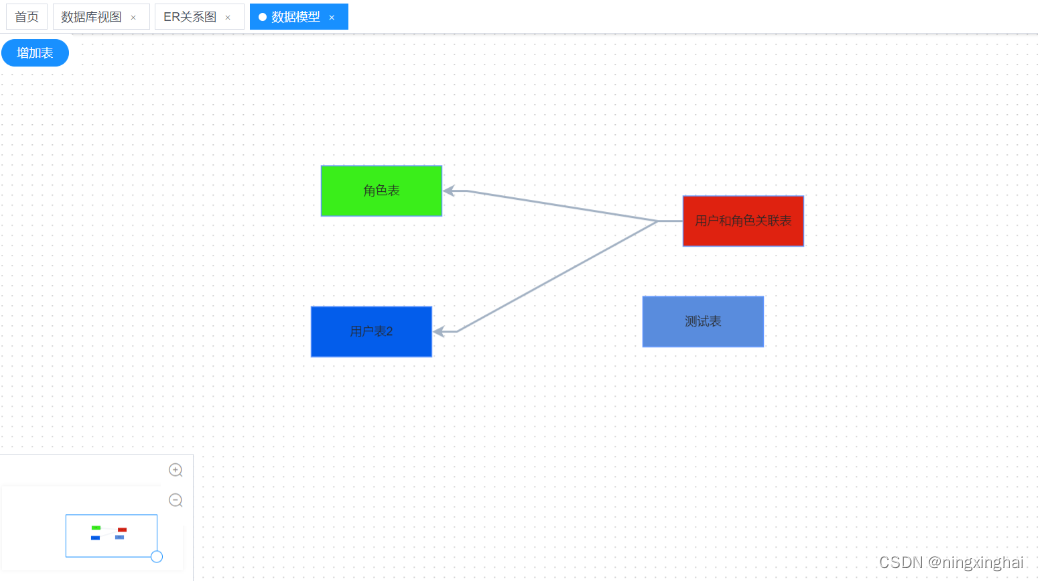
如何用国产DBDesginer软件进行数据库建模设计?
我们在开发软件系统之前都需要进行数据结构的建模设计,传统的都是通过PowerDesiger等国外的软件或直接Excel来进行数据库表结构设计,今天来了解一下如何使用国产软件来进行数据库建模设计 1、首先是注册DBDesigner用户( http://dbdesigner.n…...

精选 100 种最佳 AI 工具大盘点
为了应对对精简流程和数据分析日益增长的需求,整合人工智能工具在多个领域变得至关重要。 本文精选了2023年可用的100种最佳人工智能工具,旨在提高您的生产力、创造力和效率。 以下是 2023 年排名前 100 的人工智能工具: Aidoc:A…...

Recognizing Micro-Expression in Video Clip with Adaptive Key-Frame Mining阅读笔记
本文主要贡献 据我们所知,这是第一项旨在将视频剪辑中的信息时间子集的端到端学习与单个网络中的微表情识别相结合的工作。 此外,所提出网络中所有模块的设计都与输入视频剪辑的长度无关。 换句话说,网络容忍各种长度的微表情剪辑。 本文的贡…...
【SpringBoot整合RabbitMQ(上)】
一、简单的生产者-消费者 1.1、创建连接工具类获取信道 public class RabbitMqUtils {public static Channel getChannel() throws IOException, TimeoutException {//创建一个链接工厂ConnectionFactory factory new ConnectionFactory();//工厂IP 链接RabbitMQ的队列facto…...
Linux 设备驱动程序(二)
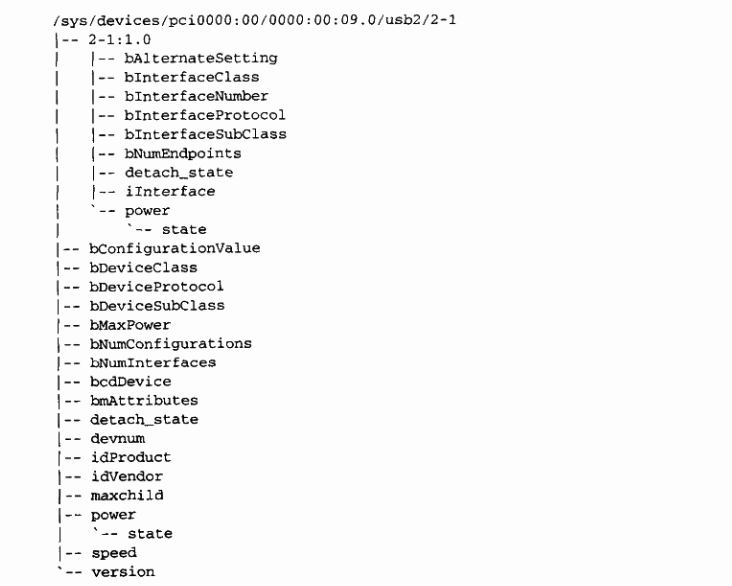
系列文章目录 Linux 内核设计与实现 深入理解 Linux 内核(一) 深入理解 Linux 内核(二) Linux 设备驱动程序(一) Linux 设备驱动程序(二) Linux设备驱动开发详解 文章目录 系列文章目…...

性价比提升15%,阿里云发布第八代企业级计算实例g8a和性能增强型实例g8ae
5 月 17 日,2023 阿里云峰会常州站上,阿里云正式发布第八代企业级计算实例 g8a 以及性能增强性实例 g8ae。两款实例搭载第四代 AMD EPYC 处理器,标配阿里云 eRDMA 大规模加速能力,网络延时低至 8 微秒。其中,g8a 综合性…...

Unity VR开发教程 OpenXR+XR Interaction Toolkit 番外(一)用 Grip 键, Trigger 键和摇杆控制手部动画
文章目录 📕制作手部动画📕设置 Animation Controller📕添加触摸摇杆的 Input Action📕代码部分 在大部分 VR 游戏中,手部的动画通常是由手柄的三个按键来控制的。比如 Grip 键控制中指、无名指、小拇指的弯曲…...
H.265/HEVC编码原理及其处理流程的分析
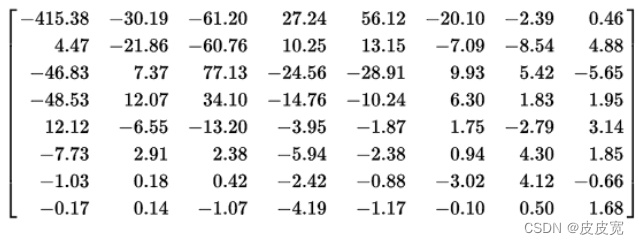
H.265/HEVC编码原理及其处理流程的分析 H.265/HEVC编码的框架图,查了很多资料都没搞明白,各个模块的处理的分析网上有很多,很少有把这个流程串起来的。本文的主要目的是讲清楚H.265/HEVC视频编码的处理流程,不涉及复杂的计算过程。…...

数据结构初阶--链表OJⅡ
目录 前言相交链表思路分析代码实现 环形链表思路分析代码实现 环形链表Ⅱ思路分析代码实现 复制带随机指针的链表思路分析代码实现 前言 本篇文章承接上篇博客,继续对部分经典链表OJ题进行讲解 相交链表 先来看题目描述 思路分析 这道题我们还是首先来判断一…...

离职or苟住?
面对不太好的大环境,我们什么时候该离职,什么时候不应该离职呢?分享几个观点,希望对你有所启发。 以前就有大佬讲过,离职无非是两个原因,一是因为薪资不到位,二是因为受委屈了,总之&…...
微服务之以nacos注册中心,以gateway路由转发服务调用实例(第一篇)
实现以nacos为注册中心,网关路由转发调用 项目版本汇总项目初始化新建仓库拉取仓库项目父工程pom初始化依赖版本选择pom文件如下 网关服务构建pom文件启动类配置文件YMLnacos启动新建命名空间配置网关yml(nacos)网关服务启动 用户服务构建pom文件启动类配置文件YML新增url接口配…...

主成分分析(PCA)直观理解与数学推导
近期在完成信息论的作业,发现网上的资料大多是直观解释,对其中的数学原理介绍甚少,并且只介绍了向量降维,而没有介绍向量重构的问题(重构指的是:根据降维后的低维向量来恢复原始向量)࿰…...

什么是合伙企业?普通合伙和有限合伙区别?
1.什么是合伙企业? 合伙企业是指由各合伙人订立合伙协议,共同出资,共同经营,共享收益,共担风险,并对企业债务承担无限连带责任的营利性组织。合伙企业一般无法人资格,不缴纳企业所得税,缴纳个…...

系统结构考点之不明白的点
系统结构考点系列 计算机系统结构的定义计算机组成的定义计算机实现的定义计算系统的定量设计?1. 哈夫曼压缩原理2. Amdahl定律3. cpu性能公式4. 程序访问局部性定理 这样的题已经不多了,主要是要了解下概念。打下一个好的基础。 2023年4月份成绩已经…...

Android中AIDL的简单使用(Hello world)
AIDL:Android Interface Definition Language(Android接口定义语言) 作用:跨进程通讯。如A应用调用B应用提供的接口 代码实现过程简述: A应用创建aidl接口,并且创建一个Service来实现这个接口(…...

ZED使用指南(五)Camera Controls
七、其他 1、相机控制 (1)选择视频模式 左右视频帧同步,以并排格式作为单个未压缩视频帧流式传输。 在ZED Explorer或者使用API可以改变视频的分辨率和帧率。 (2)选择输出视图 ZED能以不同的格式输出图像…...

wrk泛洪攻击监控脚本
wrk泛洪攻击介绍 WRK泛洪攻击(WRK Flood Attack)是一种基于WRK工具进行的DDoS攻击(分布式拒绝服务攻击)。WRK是一个高度并行的HTTP负载生成器,可以模拟大量用户访问一个网站,从而导致该网站服务器瘫痪或失效…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...
