主成分分析(PCA)直观理解与数学推导
近期在完成信息论的作业,发现网上的资料大多是直观解释,对其中的数学原理介绍甚少,并且只介绍了向量降维,而没有介绍向量重构的问题(重构指的是:根据降维后的低维向量来恢复原始向量),因此在这里做一个总结,配合另一篇博客看效果可能会更好参考博客。
简介
PCA降维就是要把 m m m维空间的n个样本点 x i , i = 1 ⋯ n x_i,i=1\cdots n xi,i=1⋯n映射成 l l l维的低维空间中的向量 y i , i = 1 ⋯ n y_i,i=1\cdots n yi,i=1⋯n,其中 l ≪ m l\ll m l≪m。这个映射不是随意的,而是要确保利用低维的向量 y i y_i yi重构出的 x i ′ x_i^{'} xi′与原向量 x i x_i xi的误差最小化。这个过程可以描述成
y l × 1 = W l × m x m × 1 y_{l\times1}=W_{l\times m}x_{m\times1} yl×1=Wl×mxm×1
于是PCA的任务就是找到这样一个W矩阵。
算法数学推导
我们考虑一个二维空间中的数据压缩成一维的问题:
给定五个样本点 x i , i = 1 ⋯ 5 x_i,i=1\cdots5 xi,i=1⋯5,每个样本点都是一个二维的列向量,把它们拼成一个矩阵 X = ( x 1 , x 2 , x 3 , x 4 , x 5 ) = [ 1 1 2 4 2 1 3 3 4 4 ] X=(x_1,x_2,x_3,x_4,x_5)=\begin{bmatrix}1&1&2&4&2\\1&3&3&4&4\end{bmatrix} X=(x1,x2,x3,x4,x5)=[1113234424]。
这个例子和文章开头提到的那篇博客中的例子是一致的,可以参考那篇博客的图片。
我们知道每个向量是通过一组基和在这组基下的坐标来描述的,例如 x 1 = [ 1 , 1 ] T x_1=[1,1]^T x1=[1,1]T是该向量在单位正交基 ξ 1 = [ 0 , 1 ] T , ξ 2 = [ 1 , 0 ] T \xi_1=[0,1]^T,\xi_2=[1,0]^T ξ1=[0,1]T,ξ2=[1,0]T下的坐标表示,坐标实际上就是向量向各个基上的投影值。同样的,如果我们要将一个二维向量压缩成一维向量,那么只需要找到一条直线,直线的单位方向向量 w w w作为基,然后用向量向这条直线的投影值就可以描述压缩后的一维向量。
一条直线可以用它经过的点 μ \mu μ和单位方向向量 w w w来描述,即 x = μ + α w x=\mu+\alpha w x=μ+αw,(这里我们用的 μ \mu μ是上述五个样本点的均值 [ 2 , 3 ] T [2,3]^T [2,3]T)这里的 α \alpha α就可以理解为坐标, w w w是基。那么我们要寻找的二维向量 x i x_i xi经过压缩后的一维向量其实就是 α i \alpha_i αi,现在需要确定 w w w,这样才能求出二维向量向直线的投影值。正如前一节所述,这个 w w w不是任意的,而是应该确保重构后的误差最小化,它可以描述成如下的优化问题:
min w f ( w ) = 1 2 ∑ i = 1 n ∥ ( μ + α i w ) − x i ∥ 2 2 \min _{w} f(w)=\frac{1}{2} \sum_{i=1}^n\left\|\left(\mu+\alpha_i w\right)-x_i\right\|_2^2 wminf(w)=21i=1∑n∥(μ+αiw)−xi∥22
先求出 α i \alpha_i αi的取值,
∂ f ∂ α i = w T ( μ + α i w − x i ) = 0 \frac{\partial f}{\partial \alpha_i}=w^T(\mu+\alpha_iw-x_i)=0 ∂αi∂f=wT(μ+αiw−xi)=0
由于 w w w是单位向量,即 w T w = 1 w^Tw=1 wTw=1,由上式可得:
α i = w T ( x i − μ ) \alpha_i=w^T(x_i-\mu) αi=wT(xi−μ)
这个公式就给出了 α i \alpha_i αi的求解方法。下面继续推导确定 w w w的过程,定义散布矩阵如下:
S = ∑ i = 1 n ( x i − μ ) ( x i − μ ) T S=\sum_{i=1}^n(x_i-\mu)(x_i-\mu)^T S=i=1∑n(xi−μ)(xi−μ)T
对于上面的例子,我们把 X X X中的每个样本 x i x_i xi都减去均值 μ \mu μ得到一个新的矩阵记为 X ~ = [ − 1 − 1 0 2 0 − 2 0 0 1 1 ] \tilde{X}=\begin{bmatrix}-1&-1&0&2&0\\-2&0&0&1&1\end{bmatrix} X~=[−1−2−10002101],那么上面的散步矩阵其实可以简单地记为
S = X ~ X ~ T S=\tilde{X}\tilde{X}^T S=X~X~T
说明它是一个对称矩阵。
将上面求出的 α i \alpha_i αi的表达式代入到 f ( w ) f(w) f(w)中,得到:
f ( w ) = 1 2 ∑ i = 1 n ∥ α i w − ( x i − μ ) ∥ 2 2 = 1 2 ( ∑ i = 1 n α i 2 ∥ w ∥ 2 2 − 2 ∑ i = 1 n α i w T ( x i − μ ) + ∑ i = 1 n ∥ x i − μ ∥ 2 2 ) = − 1 2 ∑ i = 1 n α i 2 + 1 2 ∑ i = 1 n ∥ x i − μ ∥ 2 2 = − 1 2 ∑ i = 1 n [ w T ( x i − μ ) ] 2 + 1 2 ∑ i = 1 n ∥ x i − μ ∥ 2 2 = − 1 2 ∑ i = 1 n w T ( x i − μ ) ( x i − μ ) T w + 1 2 ∑ i = 1 n ∥ x i − μ ∥ 2 2 = − 1 2 w T ( ∑ i = 1 n ( x i − μ ) ( x i − μ ) T ) w + 1 2 ∑ i = 1 n ∥ x i − μ ∥ 2 2 = − 1 2 w T S w + 1 2 ∑ i = 1 n ∥ x i − μ ∥ 2 2 \begin{aligned} f(\boldsymbol{w}) & =\frac{1}{2} \sum_{i=1}^n\left\|\alpha_i \boldsymbol{w}-\left(\boldsymbol{x}_i-\boldsymbol{\mu}\right)\right\|_2^2 \\ & =\frac{1}{2}\left(\sum_{i=1}^n \alpha_i^2\|\boldsymbol{w}\|_2^2-2 \sum_{i=1}^n \alpha_i \boldsymbol{w}^{\mathrm{T}}\left(\boldsymbol{x}_i-\boldsymbol{\mu}\right)+\sum_{i=1}^n\left\|\boldsymbol{x}_i-\boldsymbol{\mu}\right\|_2^2\right) \\ & =-\frac{1}{2} \sum_{i=1}^n \alpha_i^2+\frac{1}{2} \sum_{i=1}^n\left\|\boldsymbol{x}_i-\boldsymbol{\mu}\right\|_2^2 \\ & =-\frac{1}{2} \sum_{i=1}^n\left[\boldsymbol{w}^{\mathrm{T}}\left(\boldsymbol{x}_i-\boldsymbol{\mu}\right)\right]^2+\frac{1}{2} \sum_{i=1}^n\left\|\boldsymbol{x}_i-\boldsymbol{\mu}\right\|_2^2 \\ & =-\frac{1}{2} \sum_{i=1}^n \boldsymbol{w}^{\mathrm{T}}\left(\boldsymbol{x}_i-\boldsymbol{\mu}\right)\left(\boldsymbol{x}_i-\boldsymbol{\mu}\right)^{\mathrm{T}} \boldsymbol{w}+\frac{1}{2} \sum_{i=1}^n\left\|\boldsymbol{x}_i-\boldsymbol{\mu}\right\|_2^2 \\ & =-\frac{1}{2} \boldsymbol{w}^{\mathrm{T}}\left(\sum_{i=1}^n\left(\boldsymbol{x}_i-\boldsymbol{\mu}\right)\left(\boldsymbol{x}_i-\boldsymbol{\mu}\right)^{\mathrm{T}}\right) \boldsymbol{w}+\frac{1}{2} \sum_{i=1}^n\left\|\boldsymbol{x}_i-\boldsymbol{\mu}\right\|_2^2 \\ & =-\frac{1}{2} \boldsymbol{w}^{\mathrm{T}} S \boldsymbol{w}+\frac{1}{2} \sum_{i=1}^n\left\|\boldsymbol{x}_i-\boldsymbol{\mu}\right\|_2^2 \end{aligned} f(w)=21i=1∑n∥αiw−(xi−μ)∥22=21(i=1∑nαi2∥w∥22−2i=1∑nαiwT(xi−μ)+i=1∑n∥xi−μ∥22)=−21i=1∑nαi2+21i=1∑n∥xi−μ∥22=−21i=1∑n[wT(xi−μ)]2+21i=1∑n∥xi−μ∥22=−21i=1∑nwT(xi−μ)(xi−μ)Tw+21i=1∑n∥xi−μ∥22=−21wT(i=1∑n(xi−μ)(xi−μ)T)w+21i=1∑n∥xi−μ∥22=−21wTSw+21i=1∑n∥xi−μ∥22
上式的第二项与 w w w无关,因此要极小化 f ( w ) f(w) f(w),只要使第一项极小化,于是优化问题转化为
min − 1 2 w T S w s . t . w T w = 1 \begin{aligned}\min &-\frac{1}{2}w^TSw\\ {\rm s.t.\ } &w^Tw=1\end{aligned} mins.t. −21wTSwwTw=1
这个优化问题可以用拉格朗日乘子法求解,令拉格朗日函数为
L ( w , λ ) = − 1 2 w T S w + λ 2 ( w T w − 1 ) L(w,\lambda)=-\frac{1}{2}w^TSw+\frac{\lambda}{2}(w^Tw-1) L(w,λ)=−21wTSw+2λ(wTw−1)
令
∂ L ∂ w = − S w + λ w = 0 \frac{\partial L}{\partial w}=-Sw+\lambda w=0 ∂w∂L=−Sw+λw=0
从而 S w = λ w Sw=\lambda w Sw=λw
到这里,结果已经逐渐清晰了,我们要求的 w w w正是矩阵 S S S的特征向量。稍作变形:
w T S w = λ w T w = λ w^TSw=\lambda w^Tw=\lambda wTSw=λwTw=λ
我们要最小化 − 1 2 w T S w -\frac{1}{2}w^TSw −21wTSw,就是要最大化 w T S w w^TSw wTSw,则 w w w应该是 S S S的最大特征值 λ max \lambda_{\max} λmax对应的特征向量。
算法总结
至此,我们可以总结一下二维向量压缩成一维的PCA的方法:
(1)求矩阵 S = ∑ i = 1 n ( x i − μ ) ( x i − μ ) T = X ~ X ~ T S=\sum_{i=1}^n(x_i-\mu)(x_i-\mu)^T=\tilde{X}\tilde{X}^T S=i=1∑n(xi−μ)(xi−μ)T=X~X~T
(2)求 S S S最大的特征值对应的特征向量,即 w w w
(3)求 α i = w T ( x i − μ ) \alpha_i=w^T(x_i-\mu) αi=wT(xi−μ)
于是 X = ( x 1 , x 2 , x 3 , x 4 , x 5 ) X=(x_1,x_2,x_3,x_4,x_5) X=(x1,x2,x3,x4,x5)经过压缩之后得到的结果就是 Y = ( α 1 , α 2 , α 3 , α 4 , α 5 ) Y=(\alpha_1,\alpha_2,\alpha_3,\alpha_4,\alpha_5) Y=(α1,α2,α3,α4,α5)。
投影到方向向量 w w w所对应的直线之后, w w w成了唯一的一个基,于是一维空间中的样本 x i ′ x_i^{'} xi′可以由基向量 w w w表示:
x i ′ = μ + α i w x_i^{'}=\mu+\alpha_iw xi′=μ+αiw
在原来的2维空间中,我们用基的系数来表示样本 x i x_i xi,而在1维空间中,同样以基 w w w的系数 α i \alpha_i αi来表示一维向量,它被称为主成分。
将二维向量压缩成一维向量 α i \alpha_i αi有时候只是为了减少传输时的数据量,一维向量是无法直接使用的,需要根据一维向量重构出原来的二维向量。如何重构呢?其实上面关于的 x i ′ x_i^{'} xi′的公式已经给出了答案。
二维样本PCA降维的例子
还是上面的例子,我们按照这个流程走一遍:
μ = [ 2 , 3 ] T \mu=[2,3]^T μ=[2,3]T
X ~ = X − μ = [ − 1 − 1 0 2 0 − 2 0 0 1 1 ] \tilde{X}=X-\mu=\begin{bmatrix}-1&-1&0&2&0\\-2&0&0&1&1\end{bmatrix} X~=X−μ=[−1−2−10002101]
S = X ~ X ~ T = [ − 1 − 1 0 2 0 − 2 0 0 1 1 ] [ − 1 − 2 − 1 0 0 0 2 1 0 1 ] = [ 6 4 4 6 ] S=\tilde{X}\tilde{X}^T=\begin{bmatrix}-1&-1&0&2&0\\-2&0&0&1&1\end{bmatrix}\begin{bmatrix}-1&-2\\-1&0\\0&0\\2&1\\0&1\end{bmatrix}=\begin{bmatrix}6&4\\4&6\end{bmatrix} S=X~X~T=[−1−2−10002101] −1−1020−20011 =[6446]
S的最大特征值为10,对应特征向量 w = [ 1 2 , 1 2 ] T w=[\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]^T w=[21,21]T
于是降维后的表示为:
Y = ( α 1 , α 2 , α 3 , α 4 , α 5 ) = w T X ~ = [ 1 2 , 1 2 ] [ − 1 − 1 0 2 0 − 2 0 0 1 1 ] = [ − 3 / 2 , − 1 / 2 , 0 , 3 / 2 , − 1 / 2 ] Y=(\alpha_1,\alpha_2,\alpha_3,\alpha_4,\alpha_5)=w^T\tilde{X}=[\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]\begin{bmatrix}-1&-1&0&2&0\\-2&0&0&1&1\end{bmatrix}=[-3/\sqrt{2},-1/\sqrt{2},0,3/\sqrt{2},-1/\sqrt{2}] Y=(α1,α2,α3,α4,α5)=wTX~=[21,21][−1−2−10002101]=[−3/2,−1/2,0,3/2,−1/2]
要重构第一个样本 x 1 ′ x_1{'} x1′,方法是:
x 1 ′ = μ + α 1 w = [ 2 , 3 ] T + − 3 2 [ 1 2 , 1 2 ] T = [ 1 2 , 3 2 ] T x_1^{'}=\mu+\alpha_1w=[2,3]^T+\frac{-3}{\sqrt{2}}[\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]^T=[\frac{1}{2},\frac{3}{2}]^T x1′=μ+α1w=[2,3]T+2−3[21,21]T=[21,23]T
当然,与原本的 x 1 = [ 1 , 1 ] T x_1=[1,1]^T x1=[1,1]T还是有一些误差的。
更高维的情况
前面介绍的是二维降为一维的情况,更一般地,对于 m m m维向量 x i x_i xi如果要降维为 l l l维的 y i y_i yi,算法也是类似的,不加证明地给出以下步骤:
(1)求矩阵 S = ∑ i = 1 n ( x i − μ ) ( x i − μ ) T = X ~ X ~ T S=\sum_{i=1}^n(x_i-\mu)(x_i-\mu)^T=\tilde{X}\tilde{X}^T S=i=1∑n(xi−μ)(xi−μ)T=X~X~T
(2)求 S S S的所有特征值,从大到小排列,选取前 l l l个特征值所对应的特征向量,即 W = ( w 1 , w 2 , ⋯ , w l ) W=(w_1,w_2,\cdots,w_l) W=(w1,w2,⋯,wl)。
(3)求各个样本点 x i x_i xi对应于基 w 1 , w 2 , ⋯ , w l w_1,w_2,\cdots,w_l w1,w2,⋯,wl的系数,即主成分, α i , k = w k T ( x i − μ ) , k = 1 ⋯ l \alpha_{i,k}=w_k^T(x_i-\mu),k=1\cdots l αi,k=wkT(xi−μ),k=1⋯l,得到低维的表示 y i = ( α i , 1 , α i , 2 , ⋯ α i , l ) T y_i=(\alpha_{i,1},\alpha_{i,2},\cdots \alpha_{i,l})^T yi=(αi,1,αi,2,⋯αi,l)T
这个过程可以写成矩阵的形式:
Y = W T X ~ Y=W^T\tilde{X} Y=WTX~
Y = ( y 1 , y 2 , ⋯ , y n ) Y=(y_1,y_2,\cdots,y_n) Y=(y1,y2,⋯,yn)是压缩后的样本点组成的矩阵。
(4) 原向量的重构:
x i ′ = μ + ∑ k = 1 L α i , k w k x_i^{'}=\mu+\sum_{k=1}^L\alpha_{i,k}w_k xi′=μ+k=1∑Lαi,kwk
写成矩阵的形式为:
X ′ = μ + W Y X^{'}=\mu+WY X′=μ+WY
PCA用于图像处理
原图:

PCA处理后:(选40个特征向量)

相关文章:

主成分分析(PCA)直观理解与数学推导
近期在完成信息论的作业,发现网上的资料大多是直观解释,对其中的数学原理介绍甚少,并且只介绍了向量降维,而没有介绍向量重构的问题(重构指的是:根据降维后的低维向量来恢复原始向量)࿰…...

什么是合伙企业?普通合伙和有限合伙区别?
1.什么是合伙企业? 合伙企业是指由各合伙人订立合伙协议,共同出资,共同经营,共享收益,共担风险,并对企业债务承担无限连带责任的营利性组织。合伙企业一般无法人资格,不缴纳企业所得税,缴纳个…...

系统结构考点之不明白的点
系统结构考点系列 计算机系统结构的定义计算机组成的定义计算机实现的定义计算系统的定量设计?1. 哈夫曼压缩原理2. Amdahl定律3. cpu性能公式4. 程序访问局部性定理 这样的题已经不多了,主要是要了解下概念。打下一个好的基础。 2023年4月份成绩已经…...

Android中AIDL的简单使用(Hello world)
AIDL:Android Interface Definition Language(Android接口定义语言) 作用:跨进程通讯。如A应用调用B应用提供的接口 代码实现过程简述: A应用创建aidl接口,并且创建一个Service来实现这个接口(…...

ZED使用指南(五)Camera Controls
七、其他 1、相机控制 (1)选择视频模式 左右视频帧同步,以并排格式作为单个未压缩视频帧流式传输。 在ZED Explorer或者使用API可以改变视频的分辨率和帧率。 (2)选择输出视图 ZED能以不同的格式输出图像…...

wrk泛洪攻击监控脚本
wrk泛洪攻击介绍 WRK泛洪攻击(WRK Flood Attack)是一种基于WRK工具进行的DDoS攻击(分布式拒绝服务攻击)。WRK是一个高度并行的HTTP负载生成器,可以模拟大量用户访问一个网站,从而导致该网站服务器瘫痪或失效…...
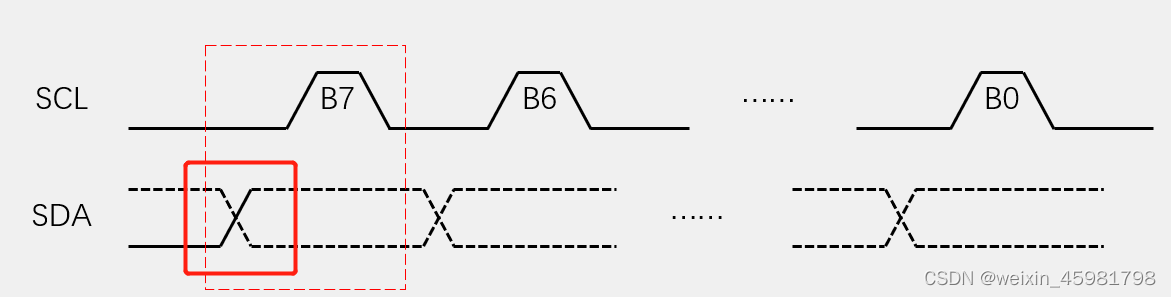
软件I2C读写MPU6050代码
1、硬件电路 SCL引到了STM32的PB10号引脚,SDA引到了PB11号引脚软件I2C协议: 用普通GPIO口,手动反转电平实现协议,不需要STM32内部的外设资源支持,故端口是可以任意指定MPU605在SCL和SDA自带了两个上拉电阻,…...

销售/回收DSOS254A是德keysight MSOS254A混合信号示波器
Agilent DSOS254A、Keysight MSOS254A、 混合信号示波器,2.5 GHz,20 GSa/s,4 通道,16 数字通道。 Infiniium S 系列示波器 信号保真度方面树立新标杆 500 MHz 至 8 GHz 出色的信号完整性使您可以看到真实显示的信号࿱…...

RIDGID里奇金属管线检测仪故障定位仪维修SR-20KIT
里奇RIDGID管线定位仪/检测仪/探测仪维修SR-20 SR-24 SR-60 美国里奇SeekTech SR-20管线定位仪对于初次使用定位仪的用户或经验丰富的用户,都同样可以轻易上手使用SR-20。SR-20提供许多设置和参数,使得大多数复杂的定位工作变得很容易。此外,…...
NodeJs之调试
关于调试 当我们只专注于前端的时候,我们习惯性F12,这会给我们带来安全与舒心的感觉。 但是当我们使用NodeJs来开发后台的时候,我想噩梦来了。 但是也别泰国担心,NodeJs的调试是很不方便!这是肯定的。 但是还好&…...
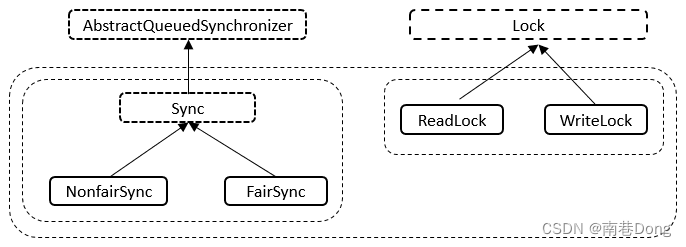
Java面试知识点(全)- Java并发-多线程JUC二-原子类/锁
Java面试知识点(全) 导航: https://nanxiang.blog.csdn.net/article/details/130640392 注:随时更新 JUC原子类 什么是CAS CAS的全称为Compare-And-Swap,直译就是对比交换。是一条CPU的原子指令,其作用是让CPU先进行比较两个值…...

CSS--移动web基础
01-移动 Web 基础 谷歌模拟器 模拟移动设备,方便查看页面效果 屏幕分辨率 分类: 物理分辨率:硬件分辨率(出厂设置)逻辑分辨率:软件 / 驱动设置 结论:制作网页参考 逻辑分辨率 视口 作用&a…...
Appuploader 常见错误及解决方法
转载:Appuploader 常见错误及解决方法 问题解决秘籍 遇到问题,第一个请登录苹果开发者官网 检查一遍账号是否有权限,是否被停用,是否过期,是否有协议需要同意,并且在右上角切换账号后检查所有关联的账号是否…...
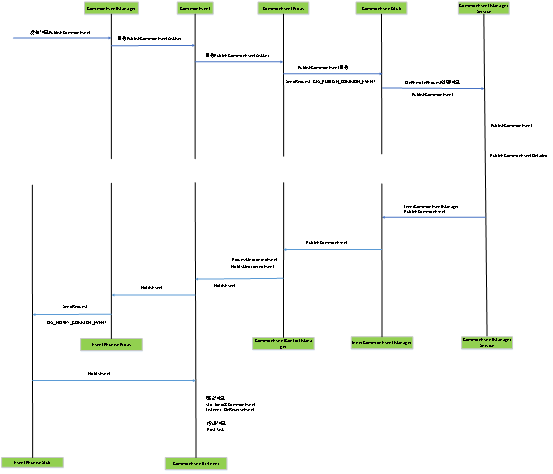
消息通知之系统层事件发布相关流程
前言 Openharmony 3.1Release中存在消息通知的处理,消息通知包括系统层事件发布、消息订阅、消息投递与处理,为了开发者能够熟悉消息的处理流程,本篇文章主要介绍系统层事件发布的相关流程。 整体流程 代码流程 发布消息 { eventAction)w…...
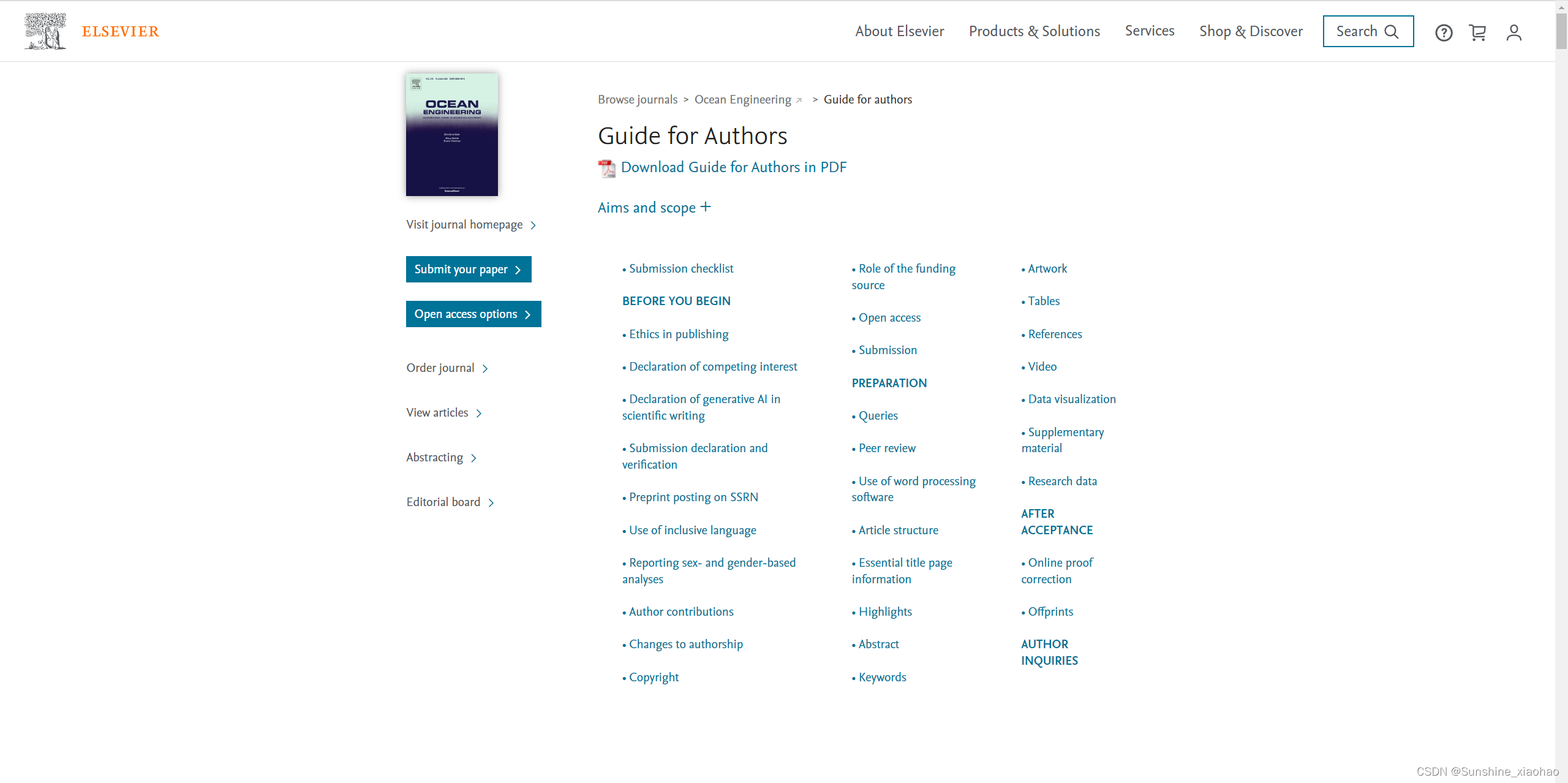
Elsevier Ocean Engineering Guide for Authors 解读
文章目录 ★Types of contributions★Submission checklistEthics in publishing★Declaration of competing interestDeclaration of generative AI in scientific writingSubmission declaration and verificationPreprint posting on SSRNUse of inclusive languageReportin…...
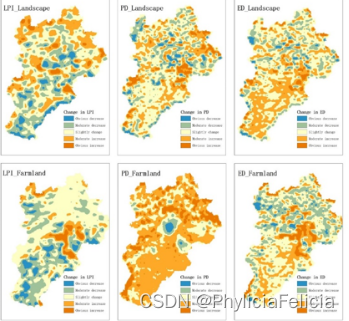
基于Fragstats的土地利用景观格局分析
土地利用以及景观格局是当前全球环境变化研究的重要组成部分及核心内容,其对区域的可持续发展以及区域土地管理有非常重要的意义。通过对土地利用时空变化规律进行分析可以更好的了解土地利用变化的过程和机制,并且通过调整人类社会经济活动,…...

ffmpeg-转码脚本02
ffmpeg-转码脚本详解 高级脚本 以下为主要部分 更高级优化要见git上 mkv转码电影脚本 ECHO OFF REM 以下参数不可乱填 SET FFMPEG%~DP0\ffmpeg.exe ::------------------------------------------------------------------------------ CALL:PRO_LOOPDIR ::CALL:PRO_LOOPDIR_SU…...

SharedPreferences
Android轻量级数据存储 import android.content.Context; import android.content.SharedPreferences;public class SharedPreferencesUtil {private SharedPreferences sharedPreferences;private SharedPreferences.Editor editor;public SharedPreferencesUtil(Context con…...
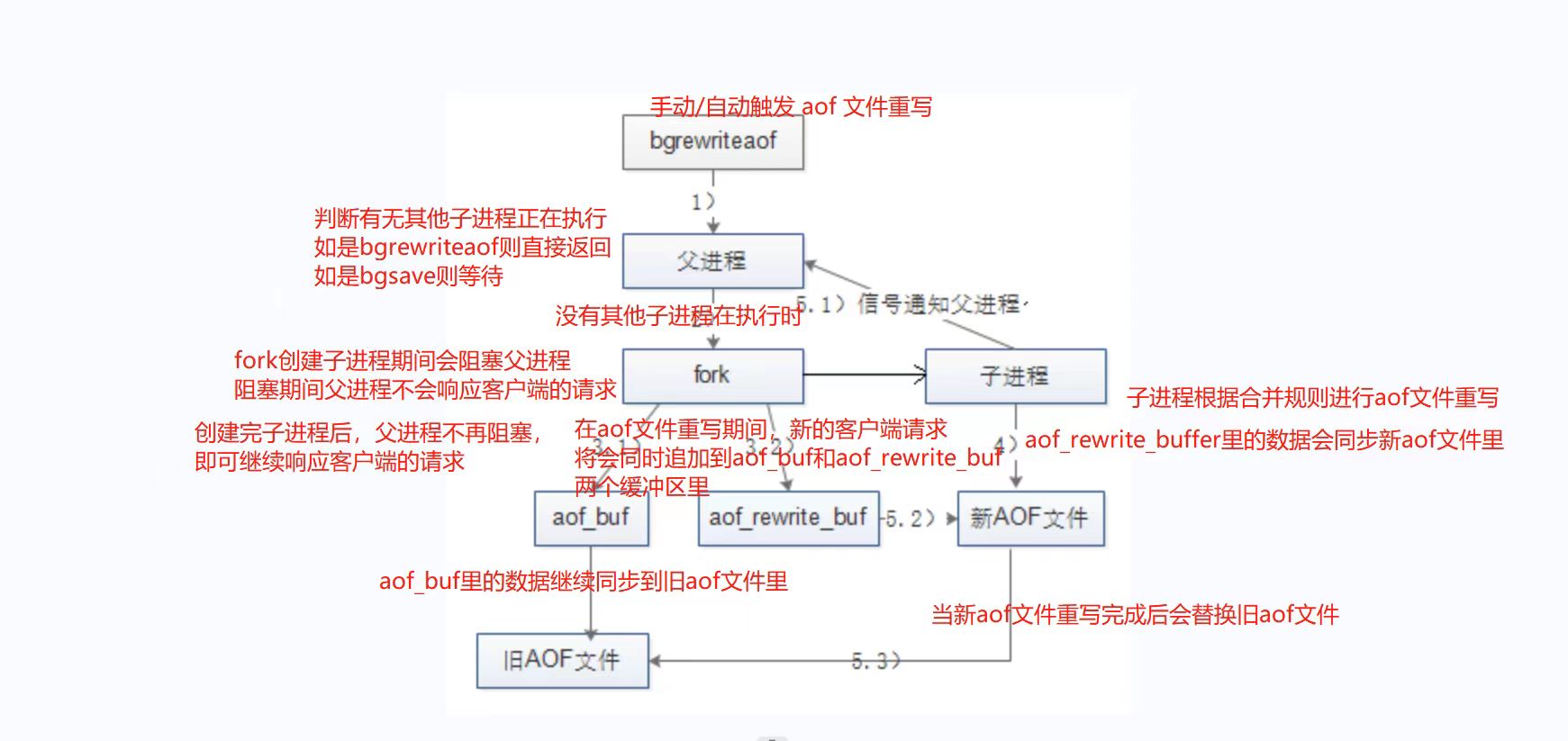
服务(第二十五篇)redis的优化和持久化
持久化的功能:Redis是内存数据库,数据都是存储在内存中,为了避免服务器断电等原因导致Redis进程异常退出后数据的永久丢失,需要定期将Redis中的数据以某种形式(数据或命令)从内存保存到硬盘;当下…...

David Silver Lecture 7: Policy Gradient
1 Introduction 1.1 Policy-Based Reinforcement Learning 1.2 Value-based and policy based RL 基于值的强化学习 在基于值的 RL 中,目标是找到一个最优的值函数,通常是 Q 函数或 V 函数。这些函数为给定的状态或状态-动作对分配一个值,表…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
