python实现斐波那契数列详解(黄金分割)
今天给各位分享一个常见的题目:求斐波那契数列前n项分别是什么(也称为黄金分割数列),整个数列需满足一个条件即第三项的值等于前两项相加的和,如第一项是1、第二项是1、第三项是2、第四项是 3、第五项是5...
满足公式:f(n+2)=f(n+1)+f(n)
拿到这个题目很多人不知道思路,接下来我会带领各位一步一步地梳理分析。
首先,我们需要定义一个函数,函数里面至少要有一个变量n来作为传值的对象,即我要求前n项的内容,所以必须要有一个n在函数中作为形式参数。
def fibo(n):pass函数构件好了之后则需要考虑初始值的问题,我们定义一个初始值的默认值为0作为记录循环轮数的变量,且会不断增长,所以还需要一个空的列表(list)来容纳接下来程序生成的数字序列。
def fibo(n):i = 0fibo_list = []由于是循环递增的,所以必不可少的就是while循环了,从而实现循环增长,我们定义一个while循环,根据题目要求(第一项和第二项为1),需要设置2个判断:
判断1:当i=0 或 i=1的时候,列表中的前两位都是1
判断2:当i大于等于2的时候,第三项的值等于第一项与第二项的和,并添加到列表
def fibo(n):i = 0fibo_list = []while i < n:if i == 0 or i == 1:fibo_list.append(1)if i >= 2:third_num = fibo_list[-1] + fibo_list[-2]fibo_list.append(third_num)写到这里,大致框架已经构建好了,只需让循环动起来并输出,调用函数时给n赋值即可,使用i += 1即可实现(i+=1等价于i = i+1)
def fibo(n):i = 0fibo_list = []while i < n:if i == 0 or i == 1:fibo_list.append(1)if i >= 2:third_num = fibo_list[-1] + fibo_list[-2]fibo_list.append(third_num)i += 1print(fibo_list)fibo(10)以上代码运行后就可以实现从第一项输出到第十项
结果如下:
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]欢迎关注,带你探秘全栈的程序世界
相关文章:
)
python实现斐波那契数列详解(黄金分割)
今天给各位分享一个常见的题目:求斐波那契数列前n项分别是什么(也称为黄金分割数列),整个数列需满足一个条件即第三项的值等于前两项相加的和,如第一项是1、第二项是1、第三项是2、第四项是 3、第五项是5... 满足公式…...

整合营销和内容营销哪个好,有什么区别
如果想做自媒体运营,不管是品牌还是个体从业者,其实都要学会如何去营销。这个也分为很多种方式,比如整合营销和内容营销。今天,来和大家谈谈整合营销和内容营销哪个好,如何才能将他们应用好? 要想回答这个问题&#x…...
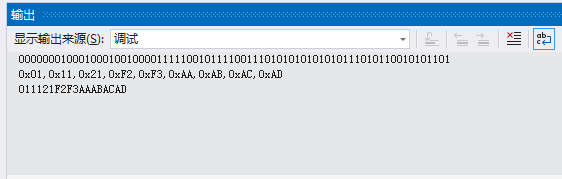
C# | [二进制字符串] 与 [字节数组] 互相转换,一行代码就搞定! - CodePlus系列
C#二进制字符串与字节数组互相转换 文章目录 C#二进制字符串与字节数组互相转换前言示例代码实现思路扩展方法说明引用CodePlus库结束语 前言 开发中有时需要将二进制数据转换为字符串或相反。虽然.NET提供了一些用于二进制数据操作的类库,但是它们的使用有时候会比…...
-Comparator#compare() 升降序确定)
Java 细节汇总(5)-Comparator#compare() 升降序确定
文章目录 1. Comparator#compare() 升降序确定升序分析 1. Comparator#compare() 升降序确定 Java 语言中 Comparator#compare(T o1, T o2) 方法的实现可以决定排序元素的升序降序,但是许多人对升降序如何确定完全没有概念。要理解升降序是如何确定的,首…...

湖北棒球发展报告·棒球5号位
湖北棒球的发展报告与办法应该考虑以下几个因素: 1. 借助政策支持。湖北棒球要想发展,政策支持是必不可少的。政府需要提供足够的资金和政策支持,以帮助俱乐部提高运营能力和加强比赛的组织。获得政府的政策支持,可以促进湖北棒球…...
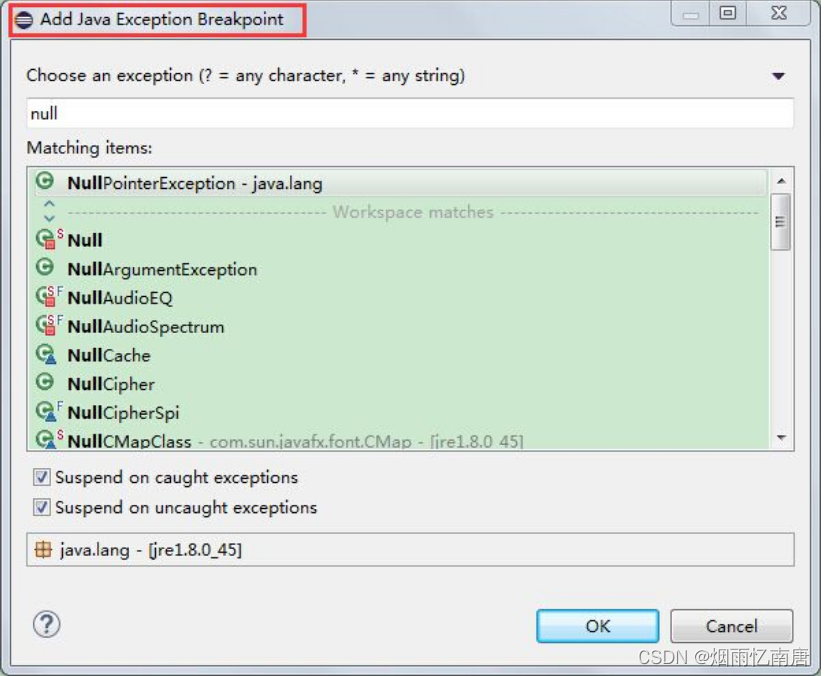
使用Eclipse 进行远程 Debug 调试
Eclipse远程调试 Java自身支持调试功能,并提供了一个简单的调试工具--JDB,类似于功能强大的GDB,JDB也是一个字符界面的调试环境,并支持设置断点,支持线程线级的调试。 由于部署环境的差异性&am…...

记第一次出差得出的经验
文章目录 1:背景2:过程3:心得 1:背景 由于上家公司的某种原因,离职来到了新公司,内中原因不足道也。新公司业务方向暂且不说,入职后,个人看着以前的产品视频学习了不到两周…...
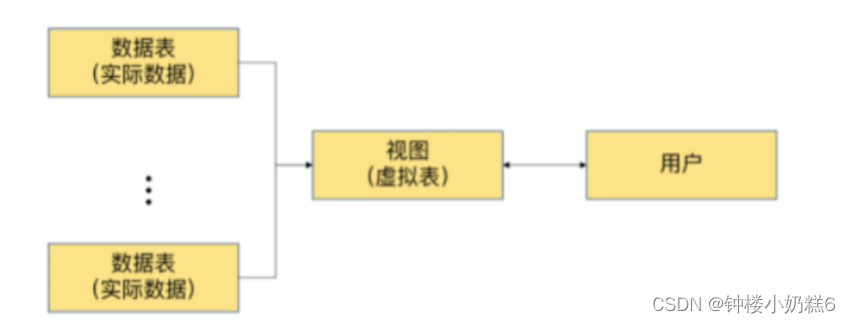
第12章:视图
一、视图 1.常见的数据库对象 ①表table:表是存储数据的逻辑单元,行和列形式存在。列是字段,行是记录。 ②数据字典:系统表,存放数据库相关信息的表。系统表的数据通常是数据库系统维护。 ③约束constraint&#x…...

Word控件Aspose.Words教程:操作 XPS 和 EPS 文档
Aspose.Words 是一种高级Word文档处理API,用于执行各种文档管理和操作任务。API支持生成,修改,转换,呈现和打印文档,而无需在跨平台应用程序中直接使用Microsoft Word。 Aspose API 支持流行文件格式处理,…...

java并发-Exchanger
## 简介 Exchanger是Java并发包中提供的一个用于线程间数据交换的工具类。它允许在两个并发任务之间进行交换对象,当第一个任务调用exchange()方法时,它会阻塞等待另一个任务也调用这个方法,然后双方交换对象,并返回结果…...
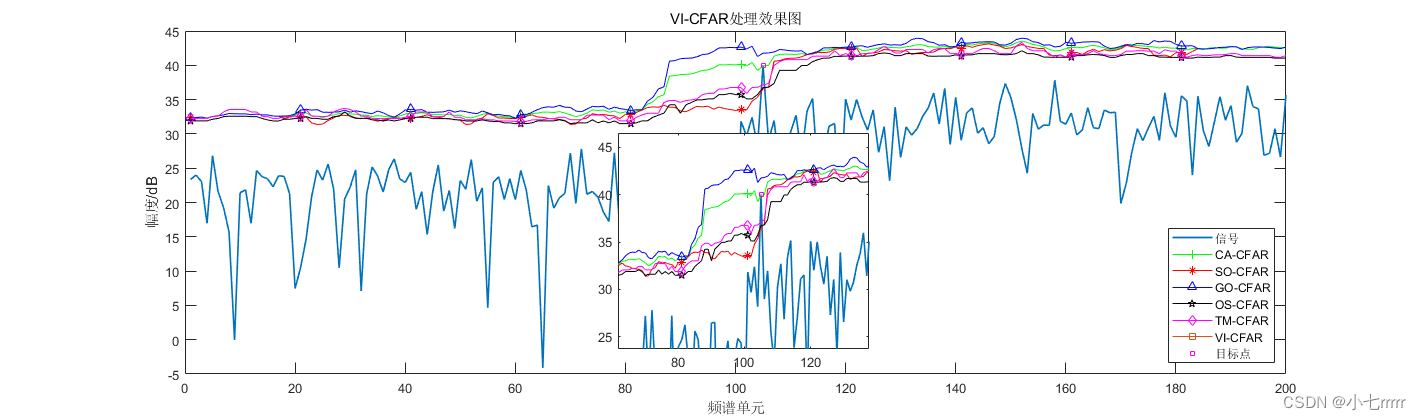
毫米波雷达系列 | 传统CFAR检测(自适应类)
毫米波雷达系列 | 传统CFAR检测(自适应类) VI-CFAR [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dV34CKJt-1684215839850)(毫米波雷达系列 传统CFAR检测(自适应类).assets/image-20230516131206695…...

【2023/05/19】NFA
Hello!大家好,我是霜淮子,2023倒计时第14天。 非确定有限状态自动机(NFA)是一种模拟复杂系统行为的数学模型 目录 一、基本概念和理论 二、优点和缺点 三、应用场景 四、问题和挑战 五、重要性、作用和使用价值 …...

汽车功能安全
前言 近些年来,功能安全在汽车传统底盘域和动力域的应用已较为成熟,各大汽车企业功能安全意识也逐渐增强。在辅助驾驶和自动驾驶爆发式增长的大趋势下,现代汽车的功能安全在目前尤为复杂的电子电气系统中就显得更为重要,功能安全…...
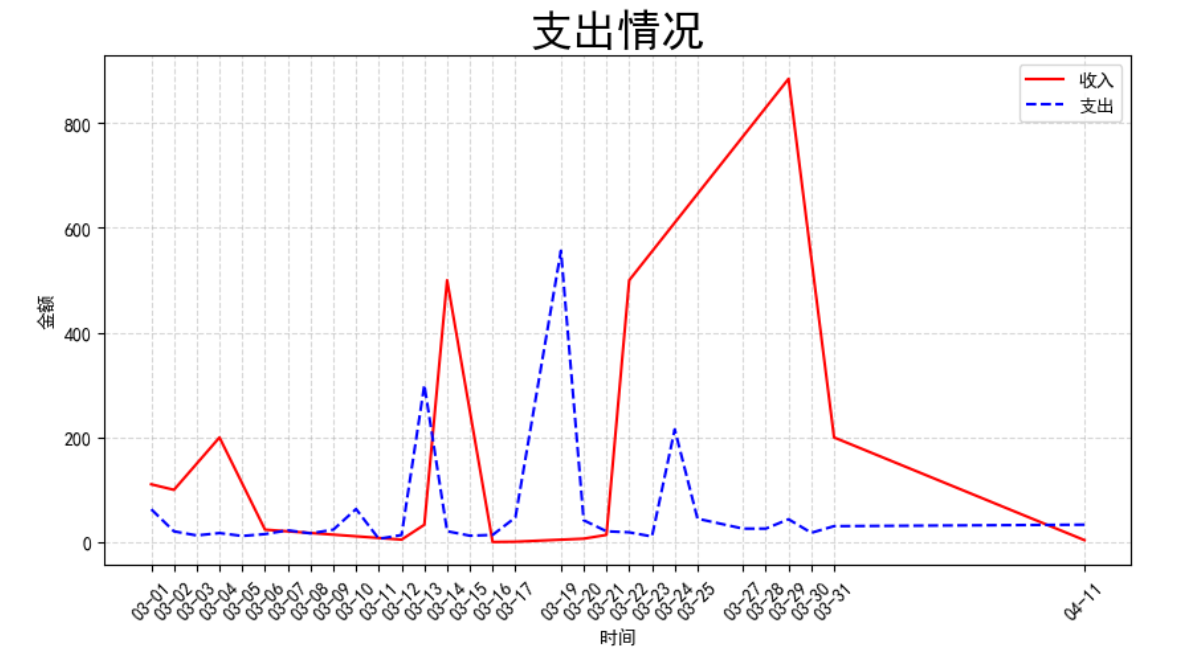
【Python】数据分析与可视化实践:收支日统计数据可视化的实现
Python数据分析与可视化实践:收支日统计数据可视化的实现 Author:萌狼蓝天 Date:2023-5-7 数据读入与基本处理 上图是原始数据的一部分,存放于excel中,首先使用pd读入数据。读入数据后,删除不是收入&#x…...

Halcon 中_xld算子的概念与应用? select_shape_std 和 select_shape_xld区别?
文章目录 1 halcon中XLD的概念与应用1.1 halcon中什么是XLD?1. 2 XLD相关算子1.2 XLD的应用1.2.1 生成XLD的操作1.2.2 选取特定xld1.2.3 3.3 XLD的合并操作2 select_shape_std 和 select_shape_xld区别2.1 select_shape_std 算子介绍2.2 select_shape_xld算子介绍2.3 select_s…...

[pgrx开发postgresql数据库扩展]7.返回序列的函数编写(3)多行表序列
前文再续,书接上一回。 上一回我们解析了如何通过pgrx编写srf,返回一个TableIterator,但是在具体应用的时候,我们还是针对一条记录返回了一行数据(多个字段的一行,也还是一行),并没…...

刚入职,就想跑路了...
刚入职一家公司,想离职又怕找不到新工作。 说实话,这个问题还是蛮常见的,很多时候,入职的公司并不是自己最满意的,即使是最满意的,入职后总会遇到各种各样的不顺心,公司制度不规范啊࿰…...

如何让技术架构师具有预知未来业务发展的能力
大家好,今天我们来分享业务架构,但是我们并不是以产品经理角度讲述一个业务架构是什么以及如何做?而是以一个技术架构师的角度,讲述如何承接业务架构或在没有业务架构的时候,如何判断业务变化趋势而对系统架构提前做出…...

卷麻了,新来的00后实在是太卷了...
在程序员职场上,什么样的人最让人反感呢? 是技术不好的人吗?并不是。技术不好的同事,我们可以帮他。 是技术太强的人吗?也不是。技术很强的同事,可遇不可求,向他学习还来不及呢。 真正让人反感的,是技术平平&…...
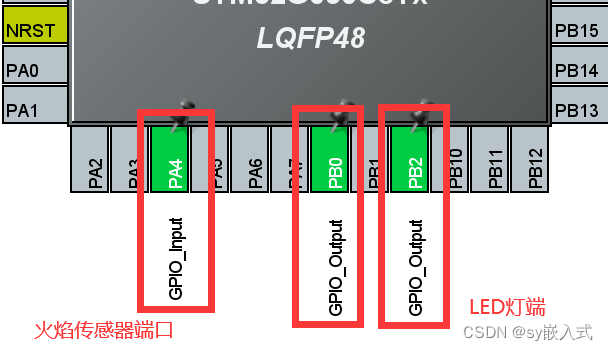
单片机--实战练习
目录 【1】GPIO 1.定义 2.应用 I - Input - 输入采集 O - Output - 输出控制 编辑编辑 3.GPIO结构框图 4.功能描述 输入功能 输出功能 5.相关寄存器 【2】点亮一盏LED灯 1.实验步骤 2.编程实现 3.编译下载 4.复位上电 练习:实现LED灯闪烁…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...
