数据结构总结1:了解数据结构、时间复杂度、空间复杂度
后续可能会有补充和更改
目录
一、数据结构
1.算法介绍
二、时间复杂度、空间复杂度
三、练习
1.时间复杂度
2.空间复杂度
一、数据结构
数据结构是计算机存储、组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的集合。
数据结构和数据库的区别
数据结构是在内存中存储管理数据的,数据库是在磁盘中存储管理数据的。
二者的本质都是存储管理数据。
内存和磁盘的区别
内存:带电存储(如果电脑突然关机,没有保存,则数据丢失。要快速访问,用内存,用数据结构)
磁盘:不带电存储(存储到数据库中、或以文件形式存储,项目当中存储的数据方便查找数据,方便遍历数据,最好用数据库存储。想持久化,长期保存下来,用数据库)
算法就是对数据按要求进行某些处理,将输入数据转换成想要的输出结果。例如:查找、排序......
二、时间复杂度、空间复杂度
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。(注意,空间复杂度不是计算程序占用了多少字节的空间,而是计算的是变量的个数。即时间复杂度算次数,空间复杂度算额外变量个数)
衡量一个算法的好坏,主要看其时间复杂度和空间复杂度,它们也是衡量性能、效率的两个主要指标。复杂度是用来计算算法中基本操作的执行次数的。实际中一般取的是算法的最差运行情况。
算复杂度不要数循环,因为它不一定准确,而是要看算法思想。
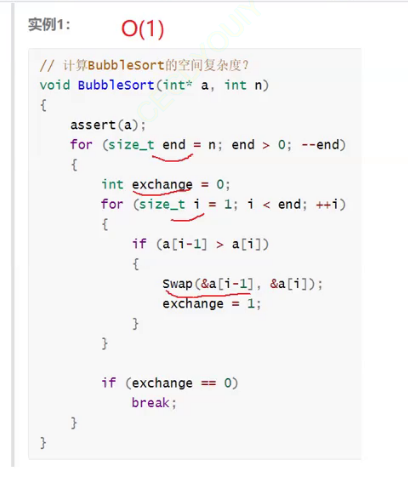
冒泡排序的时间复杂度:
二分查找的时间复杂度:O(logN)以二为底。最好情况为O(1)
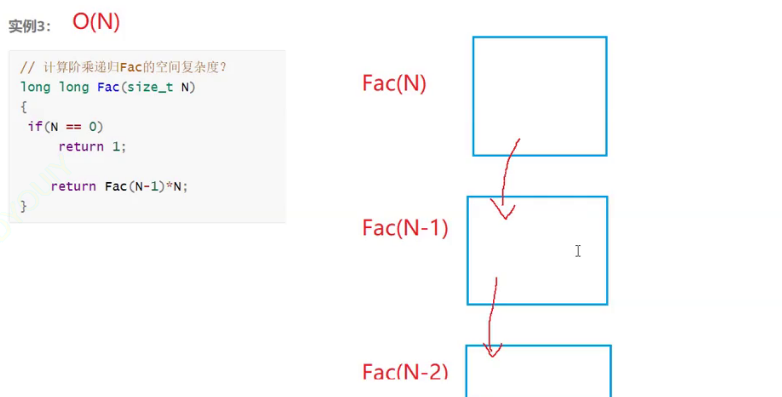
空间复杂度
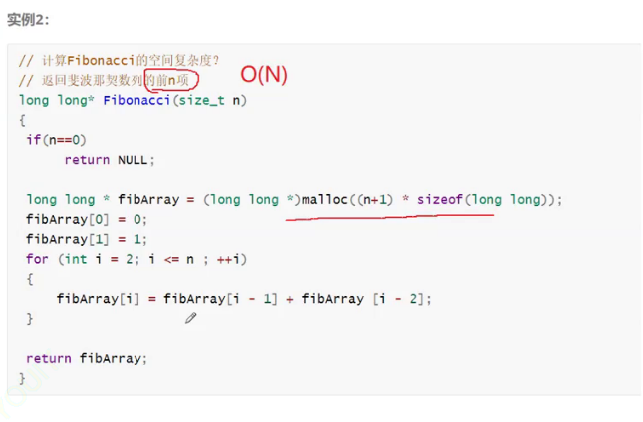
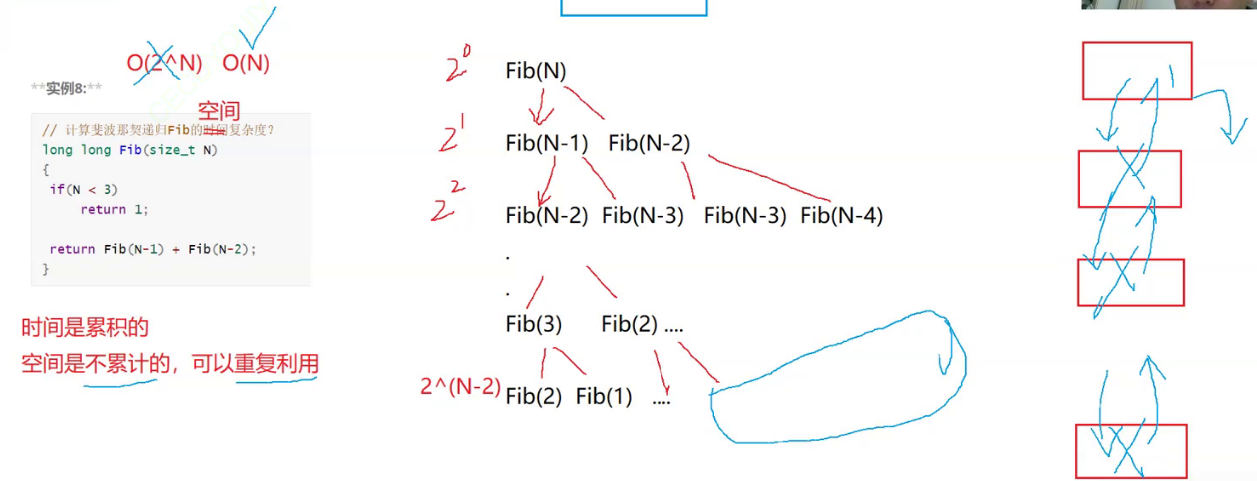
斐波那契数列的空间复杂度:O(N)
注意:时间是累积的,空间是不累积的,可以重复利用
第二节1:03:00
复杂度一般用大O的渐进表示法来表示
推导大O的方法:
1.用常数1取代运行时间中的所有加法常数(无论是多大的常数,因为现在计算机计算速度特别快,平时用到的常数次并不算多)
2.在修改后的运行次数函数中,保留最高阶项
算法中的基本操作的执行次数,为算法的时间复杂度。
3.如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
如果遇到O(N+M),N和M都是常数,这时,如果N远大于M,则是O(N),M远大于N,则是O(M),M和N一样大,就是O(N)或O(M)
O(1)表示的是常数次
函数(递归......)的时间复杂度:函数的深度及各层深度计算次数相加
很多算法大部分情况下,空间复杂的都是O(1),不是O(1)就是O(n)。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时显式申请的额外空间来决定
一般logn都是以2为底
栈的大小一般只有8MB
递归的深度太深时,空间不够 ,栈会溢出,栈溢出就是空间不够
三、练习
1.时间复杂度
1.下列有关大O表示法的说法错误的是()
A.大O表示法只是对程序执行的一个估算
B.大O表示法只保留最高阶项
C.大O表示法会保留一个系数来更准确的表示复杂度
D.大O表示法一般表示的是算法最差的运行时间
选C
大O是一个渐进表示法,不会去表示精确的次数,cpu的运算速度很快,估计精确的没有意义。
B:随着问题规模的增加,次高阶项和更低阶项对总时间的影响逐渐减小,最终可以忽略不计
C:大O表示法通常不会保留一个系数来更准确地表示复杂度,因为在算法分析中,常数项通常不是很重要,会随着具体实现方式和硬件环境的不同而变化。
2.分析以下函数的时间复杂度
void fun(int n) {int i=l;while(i<=n)i=i*2; }O(logN)
该循环并没有被执行n次,i每次都是变为自己的2倍,所以循环只会被执行log以2为底的n次
3. 分析以下程序的时间复杂度
for(int i=0;i<n;i++)for(int j=0;j<n;j++)a[i][j]=i*j;O(N^2)
程序有两次循环,每个循环都有n次操作,所以时间复杂度为n^2
4.下面算法的时间复杂度是
int f ( unsigned int n ) {if (n == 0 || n==1) return 1;else return n * f(n-1);}O(N)
此函数会被递归调用n - 1次,每次操作都是一次,所以时间复杂度为n
5.给定一个整数sum,从有N个有序元素的数组中寻找元素a,b,使得a+b的结果最接近sum,最快的平均时间复杂度是
O(N)
可以使用双指针法来解决这个问题,最快的平均时间复杂度是 O(N)
具体实现步骤如下:
1.将指针 left 指向数组的第一个元素,将指针 right 指向数组的最后一个元素。
2.计算 left 和 right 指向的元素之和。
3.如果和大于sum,则将 right 指针向左移动一位,以减小和。
如果小于sum,则将 left 指针向右移动一位,以增大和。
如果等于sum,则直接返回a和b。
在移动指针的过程中,还需记录最接近目标值的a和b,以及对应的 arr[left]和arr[right] 值。当left和right指针相遇时,结束。
因为该算法只需要遍历一次数组,每次操作都只涉及到两个指针的移动和数值的比较,因此时间复杂度是 O(N)。
6.设某算法的递推公式是T(n)=T(n-1)+n,T(0)=1,则求该算法中第n项的时间复杂度为
O(N)
T(n)
=T(n-1)+n
=T(n-2)+(n-1)+n
=T(n-3)+(n-2)+(n-1)+n
...
=T(0)+1+2+...+(n-2)+(n-1)+n
=1+1+2+...+(n-2)+(n-1)+n
该题即将T(n)推演到T(0),共递归了n次,相加次数为1+1到n,为n+1次,所以时间复杂度为O(N)
2.空间复杂度
1.如果一个函数的内部中只定义了一个二维数组a[3][6],请问这个函数的空间复杂度为
O(1)
函数内部数组的大小是固定的,空间复杂度计算的是额外空间的大小,所以不论函数运行多少次,所需空间都是固定大小的,因此空间复杂度为O(1)
2.分析以下函数的空间复杂度
int** fun(int n) {int ** s = (int **)malloc(n * sizeof(int *));while(n--)s[n] = (int *)malloc(n * sizeof(int));return s;}O(N^2)
先是为二级指针开辟空间,大小为n个一级指针。
然后分别为二级指针的每个指针开辟空间。
实际开辟后的是一个二维数组,数组有n行,每行分别有1,2,3,...n列,所以是n(n + 1)/2个元素空间。空间复杂度为O(N^2)
相关文章:
数据结构总结1:了解数据结构、时间复杂度、空间复杂度
后续可能会有补充和更改 目录 一、数据结构 1.算法介绍 二、时间复杂度、空间复杂度 三、练习 1.时间复杂度 2.空间复杂度 一、数据结构 数据结构是计算机存储、组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的集合。 数据结构和数据库的区…...

abstract class和interface有什么区别?
含有abstract修饰符的class即为抽象类,abstract 类不能创建的实例对象。含有abstract方法的类必须定义为abstract class,abstract class类中的方法不必是抽象的。abstract class类中定义抽象方法必须在具体(Concrete)子类中实现,所以…...
Kafka在Java项目中的应用
Kafka在Java项目中的应用 Docker 安装Kafka 一.首先需要安装docker,可看这篇文章安装docker 二.拉取zookeeper和KafKa镜像 docker pull wurstmeister/zookeeperdocker pull wurstmeister/kafkaKafka组件需要向zookeeper进行注册,所以也需要安装zookeeper 三.启动zookeeper…...

理解分布式id生成算法SnowFlake
理解分布式id生成算法SnowFlake 分布式id生成算法的有很多种,Twitter的SnowFlake就是其中经典的一种。 概述 SnowFlake算法生成id的结果是一个64bit大小的整数,它的结构如下图: } public function __construct(){ $this->rnew…...
光纤收发器可以连接光模块吗?
随着科技的进步发展,城市信息化速度的加快,光通信产品在数据中心和安防监控等场景中的运用越来越广泛,而这之间的连接则需要光模块和光纤收发器来实现。很多用户对光模块和光纤收发器的使用有些疑虑,两者该如何连接?又…...
一文快速了解浏览器Sui Explorer
Sui作为一条基于第一原理重新设计和构建而成的L1公链,所有区块和交易信息皆公开透明,每个人都能自行查看。通过Sui链上浏览器,用户可以迅速了解链上的交易情况,比如当前的TPS和Gas价格,也可以使用Digest来查看特定交易…...

python中lambda、yield、map、filter、reduce的使用
1、 匿名函数lambda python中允许使用lambda关键字定义一个匿名函数。所谓的匿名函数就是说使用一次或者几次之后就不再需要的函数,属于“一次性”函数。 #例1:求两数之和 f lambda x, y: x y print(f(5, 1))#例2:求平方和 print((lambda…...

第十八章 使用LNMP架构部署动态网站环境
文章目录 第十八章 使用LNMP架构部署动态网站环境一、源码包程序1、源码包的优势2、基本步骤(1)、下载及解压源码包文件(2)、编译源码包代码(3)、生成二进制安装程序(4)、运行二进制…...
无人值守的IDC机房动环综合运维方案
企业数字化转型以及5G、物联网、云计算、人工智能等新业态带动了数据中心的发展,在国家一体化大数据中心及“东数西算”节点布局的推动下,数据中心机房已成为各大企事业单位维持业务正常运营的重要组成部分,网络设备、系统、业务应用数量与日…...
桌面远程工具推荐
目前市面上的远程工具多如牛毛,很多人不知道怎么选择,下面小编介绍两种桌面远程工具,它们都是跨平台的,均支持Windows,Mac OS,IOS和安卓,分别是RayLink,VNC,好用…...
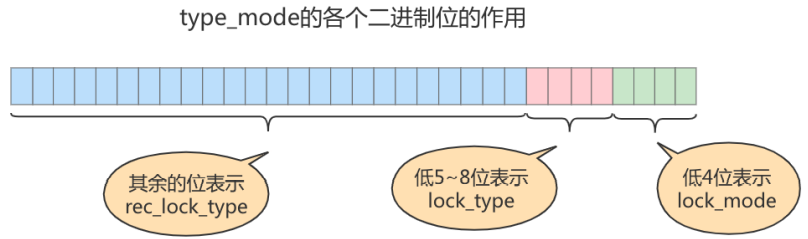
MySQL高级——第15章_锁
第15章_锁 1. 概述 锁是计算机协调多个进程或线程并发访问某一资源的机制。在程序开发中会存在多线程同步的问题,当多个线程并发访问某个数据的时候,尤其是针对一-些敏感的数据(比如订单、金额等),我们就需要保证这个数据在任何 时刻最多只…...
【ROS】Ubuntu22.04安装ROS2(Humble Hawksbill)
0、版本说明 Ubuntu22.04对应的ROS2的版本为Humble Hawksbill(ros-humble) 如果不是在Ubuntu22.04中安装ROS,请参考下面Ubuntu和ROS的版本对应关系 1、更新apt包列表 $ sudo apt update2、设置编码 将ubuntu环境语言编码设置为en_US en_…...
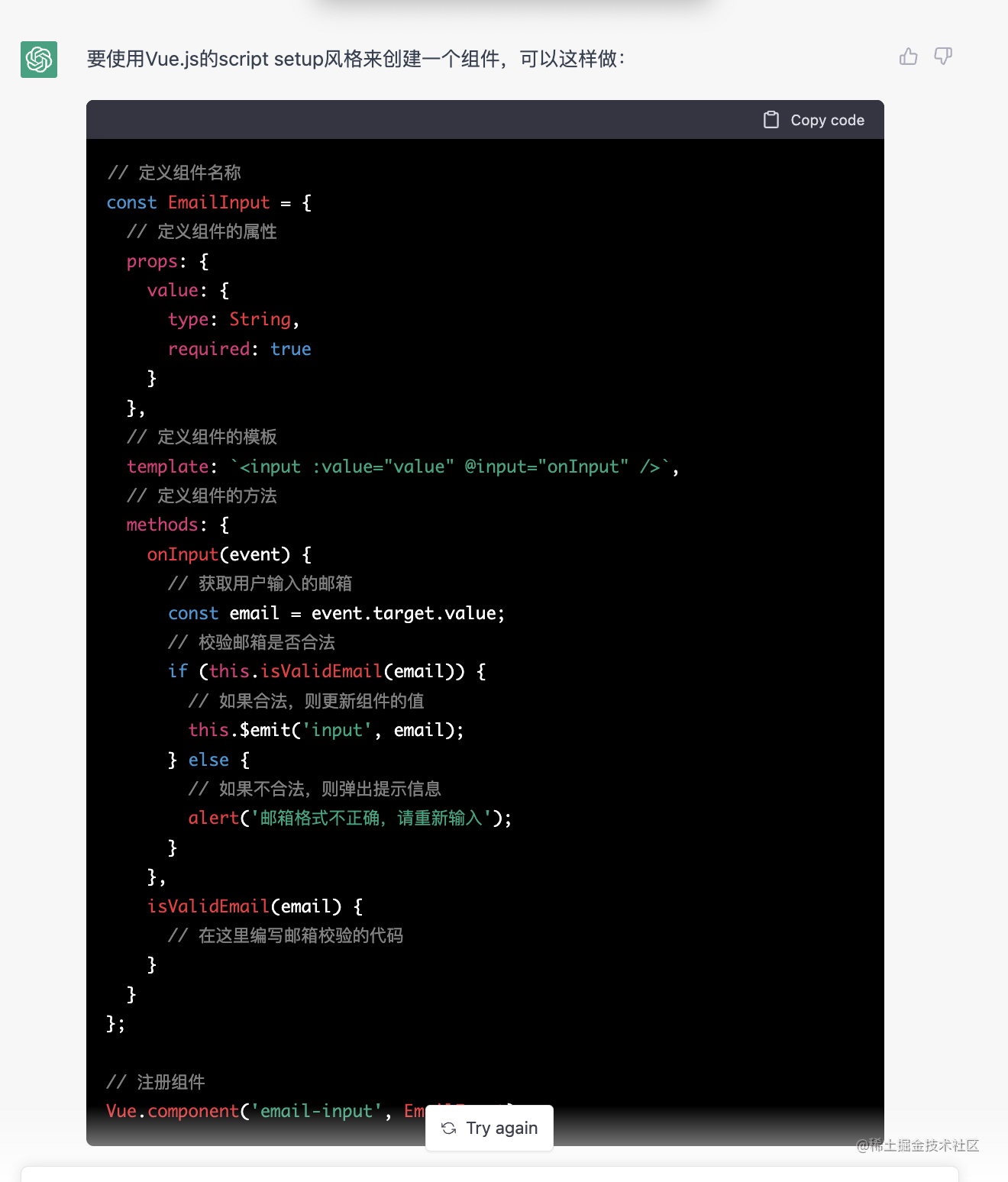
【ChatGPT】体验一下ChatGPT
体验一下ChatGPT 可以帮你写代码、写邮件、编故事的神器 最近OpenAI 发布了备受期待的原型通用 ChatGPT,这是一种基于对话的 AI 聊天界面,算是GPT-3(Generative Pre-trained Transformer 3)的继承者,今天记录一下体验的过程,以前…...

Android 串口通信
可以使用开源usb-serial-for-android 库进行串口通信 添加 usb-serial-for-android 依赖项到项目中。在项目的 build.gradle 文件中添加以下内容: dependencies {// 其他依赖项...implementation com.github.mik3y:usb-serial-for-android:3.5.1// 其他依赖项... …...

Python3 日期和时间
Python 3 提供了强大的日期和时间处理模块,名为 datetime。它可以用于执行日期和时间的各种操作,包括创建、格式化、比较和计算等。 下面是一些常用的日期和时间操作的示例: ### 获取当前日期和时间 要获取当前日期和时间,可以使…...

Go 爬虫三种框架的基本使用介绍
目录 Go 爬虫三种框架的基本使用介绍1. Colly2. Golang.org/x/net/html3. GoQuery Go 爬虫示例使用Go中的http包进行爬虫Step 1:导入包Step 2:发送请求Step 3:读取响应Step 4:解析HTMLStep 5:总结 使用Colley爬虫 结语…...
)
python实现斐波那契数列详解(黄金分割)
今天给各位分享一个常见的题目:求斐波那契数列前n项分别是什么(也称为黄金分割数列),整个数列需满足一个条件即第三项的值等于前两项相加的和,如第一项是1、第二项是1、第三项是2、第四项是 3、第五项是5... 满足公式…...

整合营销和内容营销哪个好,有什么区别
如果想做自媒体运营,不管是品牌还是个体从业者,其实都要学会如何去营销。这个也分为很多种方式,比如整合营销和内容营销。今天,来和大家谈谈整合营销和内容营销哪个好,如何才能将他们应用好? 要想回答这个问题&#x…...
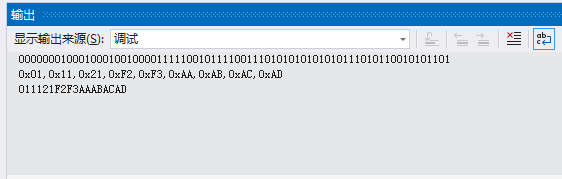
C# | [二进制字符串] 与 [字节数组] 互相转换,一行代码就搞定! - CodePlus系列
C#二进制字符串与字节数组互相转换 文章目录 C#二进制字符串与字节数组互相转换前言示例代码实现思路扩展方法说明引用CodePlus库结束语 前言 开发中有时需要将二进制数据转换为字符串或相反。虽然.NET提供了一些用于二进制数据操作的类库,但是它们的使用有时候会比…...
-Comparator#compare() 升降序确定)
Java 细节汇总(5)-Comparator#compare() 升降序确定
文章目录 1. Comparator#compare() 升降序确定升序分析 1. Comparator#compare() 升降序确定 Java 语言中 Comparator#compare(T o1, T o2) 方法的实现可以决定排序元素的升序降序,但是许多人对升降序如何确定完全没有概念。要理解升降序是如何确定的,首…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...