JavaScript刷LeetCode拿offer-贪心算法
前言
学习算法的时候,总会有一些让人生畏的名词,比方动态规划,贪心算法 等,听着就很难;而这一 part 就是为了攻破之前一直没有系统学习的 贪心算法;
有一说一,做了这些贪心题,其实并没觉得发现了什么套路新大陆等,因为贪心有的时候很巧妙,而且想到就是想到了,没想到可能就不用贪心去做了,所以这属于做完只是刷了存在感的 part;
唯一的收获就是减轻了对贪心的恐惧,明白它也就是一种 局部贪心导致全局贪心得到最优解 的一种思路方法,所以以后遇到了,也就能心平气和的去学习使用它了;
下一 part 去做一下比较难的并查集
正文
455. 分发饼干
分析 – 贪心
- 用最大的饼干满足胃口最大的小孩,这样就能局部最优求出全局最优,可以满足最多的小孩
- 由于 g,s 都需要取最大,所以需要排序
- 最后用两个端套的遍历找出最优解
- 时间复杂度 O(n+m)
var findContentChildren = function (g, s) {g.sort((a,b) => a-b)s.sort((a,b) => a-b)let ret = 0let sl = s.length-1; let gl = g.length-1while(gl>=0){// 人没了,饼干可以还存在if(s[sl]>=g[gl] && sl>=0){// 最大的饼干能否满足最大胃口的孩子ret++sl--}gl--}return ret
}
376. 摆动序列
分析 – 贪心
- 连续数字之间差值是正负交替的,叫做摆动序列;
- 边缘情况,如果只有1个值,或者两个不相等的值,也是摆动序列
- 如果出现 0, 则直接不是摆动序列了
- 如果局部符合要求,按照条件局部删除不符合要求的值,就是贪心的做法
- 时间复杂度 O(n)
var wiggleMaxLength = function(nums) {if(nums.length<2) return nums.lengthlet ret = 1 // 从 1 开始是因为要求的是整个摆动序列的长度,所以先初始化1,然后遇到极值递增即可let preDiff = 0 // 初始化第一个差值;设置为0,则无论真正第一个差值是多少,得到的都是 0let curDiff = 0for(let i = 1;i<nums.length;i++){curDiff = nums[i]- nums[i-1]// 差值必须是正负数,如果是 0 则跳过if(curDiff === 0) continueif(preDiff * curDiff <= 0){ret++preDiff = curDiff}}return ret
};
53. 最大子序和
分析 – 贪心
- 求的是最大和的
连续子数组 - 用 sum 缓存前面和大于 0 的子数组之和,一旦小于 0 ,就不再累加,重新置 0, 保持每一次迭代前 sum 的值都是 >=0
- 这样对于每一个局部子数组,它的累加值都是大于等于 0 的,这样每次累加一个新值,就进行最大值比较,保证整体是一个最大子数组之和
- 时间复杂度 O(n)
var maxSubArray = function (nums) {let max = -Infinity;let sum = 0for(let i = 0 ;i<nums.length;i++){sum+=nums[i]max = Math.max(sum,max)if(sum<=0){sum=0}}return max
};
55. 跳跃游戏
分析 – 回溯 – 超时了
- 直接将所有可能性写出来,将对应不合适的移除
- 时间复杂度 n∗m 其中 n 是nums 的长度,m 是每一个值的大小
var canJump = function (nums) {let ret = false;const dfs = (start) => {// 只要有一个成功,就直接不做其他处理了if (start >= nums.length || ret) return;if (start+nums[start] >= nums.length-1) {ret = true;return;}for (let i = 1; i <= nums[start]; i++) {dfs(start + i); // 在当前这一个节点,可以跳的步数}};dfs(0)return ret;};
分析
- 这里只要不遇到值为 0 就可以继续往后走,也就是局部贪心就是要跳过值为 0 的步骤
- 当然如果 0 是在数组最后一位也是 ok 的
- 我们可以判断一下是否存在一个值 nums[valIndex] > 0Index - valIndex, 这样只要到达 valIndex 就可以越过 0 这个点了
- 所以我们需要遍历所有节点,找到值为 0 的节点,然后再进行跳跃判断;
- 由于我们是要走到最后一个下标,所以最后一个下标是不用判断的,所以 i 最多走到 nums.length-1 的位置
- 时间复杂度最小是 n,
参考视频:传送门
var canJump = function (nums) {for(let i=0;i<nums.length-1;i++){if(nums[i] === 0){// 开始寻找可以跳过当前 i 值的节点let valIndex = i-1while(nums[valIndex]<= i -valIndex && valIndex>=0){valIndex--}if(valIndex<0) return false}}return true}
45. 跳跃游戏 II
/** * @分析 -- 已知能到达位置,求最少跳跃次数 * 1. 看到最少,想到用 dp 做;其中 dp[i] 就是到达 i 这个位置最少需要跳跃的次数, 但是控制当前状态的变量在上一个值,感觉 dp 不太合适 * 2. 感觉用贪心+回溯会更好一点,每一次尽量远的跳,如果不行再跳回来 * 3. 然后正常超时了 */
var jump = function(nums) {if(nums.length < 2) return 0let ret = Infinityconst dfs = (index,sum) => {if(index>=nums.length-1) {// 贪心走出来的,肯定是ret = Math.min(sum,ret)return }if(sum>=ret || nums[index] === 0) return // 只要出了第一个,后面的全部不玩了for(let i = nums[index];i>0;i--){dfs(index+i,sum+1)}}dfs(0,0)return ret
};/** * @分析 * 1. 考虑到跳跃范围必须覆盖一定范围,求最小的目的,还是从后倒推前面会更舒服一点,所以考虑 dp; * 2. dp[i] 表示跳跃到 i 这个位置最小的次数 * 3. 状态转移方程: dp[i] = Math.min(dp[i-valid]+1) 这里的 valid 是值符合 nums[j]+j >= i 的 dp[j], 这样在 j 这个位置才能一次跳到 i * 4. base case: dp[0] = 0 原地蹦跶 * 5. 时间复杂度 ${O(n^2)}$ */
var jump = function(nums) {const dp = new Array(nums.length)dp[0] = 0 // 原地蹦跶for(let i=1;i<nums.length;i++){dp[i] = Infinityfor(let j = i-1;j>=0;j--){if(nums[j]+j>=i){// 这样才能从 j 跳到 idp[i] = Math.min(dp[i],dp[j]+1)}}}return dp[nums.length-1]
}/** * @分析 -- 贪心 * 1. 每一次跳动都可以缓存最大跳跃范围,这是一个范围而不是一个值,所以下一跳的时候,需要从这个范围内找到最最大跳跃的范围 * 2. 所以只要迭代每一个值,就可以找到跑到这个值的时候,最大跳跃的覆盖范围 nextIndex 的位置, 同样的,我们将上一轮的最大距离设置为 curIndex * 3. 每当迭代到 curIndex, 表明上一次跳跃的覆盖范围都已经遍历完,并且记录好了这个范围内的最大值 nextIndex 了,这个时候更改 curIndex = nextIndex * 4. 其实整个过程就是在 [curIndex,nextIndex] 中找最大范围,然后不断迭代; * 5. 只需要遍历一次就能找到结果了,所以时间复杂度 ${O(n)}$ */var jump = function(nums) {let curIndex = nextIndex = 0let ret = 0for(let i =0;i<nums.length;i++){if(curIndex >=nums.length-1) return ret // 如果最大覆盖范围已经找到了地方,那么就直接跳出遍历了nextIndex = Math.max(nextIndex,nums[i]+i) // 最远覆盖范围if(curIndex === i) {// 如果 i 到达上一次最远覆盖位置,那么 nextIndex 就是上一轮 [cur,next] 的最大距离,现在需要更新一下curIndex = nextIndex// 所谓覆盖,就是 jump 一次ret++}}
}
1306. 跳跃游戏 III
注意,这里并没有用到贪心,但是这是一个主题的题目,所以也放在一起来学习了;比较分块学习也是按组类学习,而我们真正遇到问题的时候,是不会给你打 tag 说是用啥方法做的,所以相类似的题放一起做,即便由于题目改变了,没有用到相应的技术,也值得放在一起学习一哈;
分析 – BFS
- 起点改变,跳跃也从单边转左右两边,目的地也从尽头到跳跃到 0 的位置 – 注意,以前是可以跳任意位置,现在只能左右跳两个位置,而不是范围跳跃
- 基于 BFS 将数组转成类似二叉树的 bfs 搜索, 每一个节点都可以走左右两个节点 l,r, 如果符合条件,就加入到队列中继续走
- 使用的 useSet 缓存走过的节点,进行剪枝
var canReach = function (arr, start) {const queue = [];queue.push(start);const useSet = new Set();while (queue.length) {let len = queue.length;while (len--) {const node = queue.shift();const l = node - arr[node];const r = node + arr[node];if (l >= 0 && !useSet.has(l)) {if (arr[l] === 0) return true;queue.push(l);useSet.add(l);}if (r < arr.length && !useSet.has(r)) {if (arr[r] === 0) return true;queue.push(r);useSet.add(r);}}}return false;
};
分析 – dfs
- 由于没一个点最多只能左右跳一次,所以和二叉树非常相似,可以用 bfs ,当然也可以用到 dfs
- 但是判断条件不能简单的用 node 是否在 [0,arr.length-1], 因为在左右跳的过程中会有重复的点,如果不讲重复点剪掉,不但重复计算,而且会导致死循环
- 所以用 set 缓存已经走的 node,一旦再进入就移除,这样就能完整遍历可以跳到的位置,并最终跳出 dfs 遍历,得到最终结果
- 时间复杂度 O(n), 空间复杂度 O(n)
var canReach = function (arr, start) {let ret = false;const useSet = new Set(); // 剪枝用的const dfs = (node) => {if (useSet.has(node) || ret === true) return;if (arr[node] === 0) {ret = true;return;}useSet.add(node);if (node - arr[node] >= 0) {dfs(node - arr[node]);}if (node - arr[node] < arr.length) {dfs(node + arr[node]);}};dfs(start);return ret;
};
1005. K 次取反后最大化的数组和
分析
- 我们要转换,肯定是要将负数转成正数,这样能达到最大,那么情况有两种, k 充足将所有负数转换成正数,k 不足
- 第一次贪心,如果 k 不充足的时候,要先将最大的非负数,这种情况就需要排序了,所以一开始先排个序吧 – 优先给最大的负数进行转换
- 第二次贪心,如果将所有非负数转成正数后,k 还有,那么这个时候只需要处理最小的那个值就好了;
- 我们在第一次贪心的时候是排好序去处理非负数的,所以当处理完非负数之后,index 所在的位置要不就是数组之外,要不就是原始数组第一个非负数,这个时候 index-1 就是转换后的最小非负数,他们之间的对比可以找出当前数组的最小值
- 需要注意两种特殊情况,如果入参 nums 全是非负数,则 index 不会移动,那么 nums[index-1] 就取不到,同理,如果 nums 全是负数,则 index 在数组外了,所以要把两种情况考虑进去
- 最后只需要对 min 进行反复转换,如果 k 是偶数,那么就直接不转了,如果是奇数,那么就减去 min*2
- 时间复杂度 O(nlogn)
var largestSumAfterKNegations = function(nums, k) {nums.sort((a,b)=>a-b)let index = 0while(k && nums[index] < 0){// 如果 k 还存在且当前值还是负数的时候,就转换nums[index] = - nums[index]k--index++}// 转换后 index 所在的位置就是最开始最小值非负数了,但是它有可能比转换后的最小正数小,所以要对比一下// 但是如果 index 是第一个值,也就是一开始全都是非负数的时候,这个时候就没有 index-1 了;// 同理,如果全是负数,那么 index 就不存在了let min = index=== 0 ? nums[index] : index=== nums.length?nums[index-1] :Math.min( nums[index], nums[index-1])// 先将所有负数都转成正数 -- 如果 k 还存在,那么就处理 nums[index] 就好了let sum = nums.reduce((pre,cur)=>pre+cur,0)if(k % 2) sum -= min*2return sum
};
122. 买卖股票的最佳时机 II
分析 – 贪心
- 多次交易,只有计算出每日的收益,然后将每日收益为正的收集起来就是最大收益
- 由于本题是多次交易,不需要手续费和间隔时间,
- 所以如果有连续正收益的时候,相当于连续持有,如果间隔收益,那就是在负收益第一天先卖出后,在负收益的后一天买进,一样可以得到断开的正收益,所以只要将所有正收益手机起来就好
- 这样局部收益就可以扩展成全局收益,然后就可以得到最终最大的收益了
var maxProfit = function(prices) {let ret = 0for(let i = 1;i<prices.length;i++){const temp = prices[i]-prices[i-1]if(temp>0){ret+=temp}}return ret
}
134. 加油站
分析
- 我们考虑到每次加完油,就要跑路,有一些油站油充分,那么跑完一段之后会有的剩,而有些油站油少,还得补贴一点,至于具体情况如何,我们需要计算一下,所以用 leaves 来表示跑 [i,i-1] 的净油量
- 使用贪心的思维,起始车是没油的,所以必须是 leaves[i]>=0 的时候,才有可能是起始位置,然后开始往后面走,每次判断一下是否足够下一段路的行走,如果不行,果断放弃上一次的起始点,找下一个起始点
- 如果在第一次遍历过程中,没找到一个点 ret 可以走完 [ret,len-1] 的路程,那么代表所有起点都失效了,直接返回 -1
- 如果存在,那么对于循环的车道,还得再走一遍 [0,ret-1], 如果也成功了,就返回 ret
- 在整个过程中,如果累计油量保持为非负,那么就不要更改起始位置 ret, 因为你改变了位置,情况不会更好,只会更坏,这也是贪心的本质,每一次都做最好的选择,那么在中间的时候要不放弃,要不就不要改了
- 时间复杂度 O(n), 空间复杂度 O(n)
var canCompleteCircuit = function (gas, cost) {const leaves = gas.map((g, i) => g - cost[i]); // 每一个站台加油后跑路之后,剩余值的数组,正数就是有剩余,负数就是不足,需要在某些地方补充;let ret = -1;let sum = 0; // 缓存当前油量for (let i = 0; i < leaves.length; i++) {if (leaves[i] >= 0) {if (ret === -1) {ret = i;}sum += leaves[i];continue;}if (sum + leaves[i] < 0) {// 之前那个起点已经失败了ret = -1; //恢复到 -1sum = 0;} else {sum += leaves[i]; // 继续走着}}if (ret === -1) return -1; // 如果走完这一段,sum 还存在,证明在 [ret,leaves.length-1] 是合格的,那么继续走一下 [0,ret]for (let i = 0; i < ret; i++) {if (leaves[i] >= 0) {sum += leaves[i];continue;}if (sum + leaves[i] < 0) {// 在这个循环中一旦出现不合适的,就不再走下去了,因为已经走过一次了return -1;} else {sum += leaves[i]; // 继续走着}}return ret
};
分析
- 基于上面那种贪心,其实有更好的判定方式,就是只要 gasSum >= costSum , 那么必然存在一个起点,能够让车跑完一圈,因为那些差值很大的区间,都是最后积攒大量的剩余油才会去跑的;
- 上面的第二次 [0,ret] 可以不用跑,只要判断出有一个值可以走完 [ret,len-1], 同时 gasSum >= costSum,那么这个 ret 的点就是起点了
var canCompleteCircuit = function (gas, cost) {const leaves = gas.map((g, i) => g - cost[i]); // 每一个站台加油后跑路之后,剩余值的数组,正数就是有剩余,负数就是不足,需要在某些地方补充;let ret = -1;let sum = 0; // 缓存当前油量let gasSum = 0let costSum = 0for (let i = 0; i < leaves.length; i++) {costSum+=cost[i]gasSum+=gas[i]if (leaves[i] >= 0) {if (ret === -1) {ret = i;}sum += leaves[i];continue;}if (sum + leaves[i] < 0) {// 之前那个起点已经失败了ret = -1; //恢复到 -1sum = 0;} else {sum += leaves[i]; // 继续走着}}if (gasSum<costSum) return -1; return ret
};
135. 分发糖果
分析 – 题目描述有问题
- 第二个条件应该是,只要你比临近位置的评分大,那么你就必然比临近的人分得的糖果多
- 先初始所有candies 的值为 1
- 然后分两部分处理,先和左侧分数值比较,只要比左侧大,那么 candies[i] ++
- 然后再从右往左遍历,只要比左侧的分数高,那么就进行比较,取最大值 Math.max(candies[i],cadies[i+1]+1)
- 最后得到的数组 candies 就能保证,分数更高小孩,肯定比临近分数更低的小孩的 candies 更多
- 时间复杂度 O(n)
- 这里最少的发糖就用到了贪心的思想,尽可能少的给糖,先左边局部最少给糖,然后右边局部最少给糖,然后就可以影响最终给糖的数量
var candy = function (ratings) {const len = ratings.length;const candies = new Array(len).fill(1); // 发糖果的数组for (let i = 1; i < len; i++) {if (ratings[i] > ratings[i - 1]) {candies[i] = candies[i - 1] + 1;}}for (let i = len - 2; i >= 0; i--) {if (ratings[i] > ratings[i + 1]) {candies[i] = Math.max(candies[i + 1] + 1,candies[i]); // 从右边数的时候,就要判断哪边更大了}}return candies.reduce((pre, cur) => pre + cur, 0);
};
860. 柠檬水找零
分析
- 如果能思考到局部贪心,基本就是一道遍历题
- 由于 5 元属于更小粒度的单位,在数量足够的时候可以组合成 10 元, 所以我们在给 20 元找零的时候,局部贪心的保存 5 元,这样能保证出力后续的时候更可能完成任务
- 所以剩下的就是将情况排列出来了
- 时间复杂度 O(n)
var lemonadeChange = function(bills) {let fives = 0let tens = 0for(let i =0;i<bills.length;i++){const b = bills[i] if(b === 5){fives++}if(b === 10 ) {if(fives>0){fives--tens++}else {return false}}if(b === 20){// 现在用贪心,先尽可能的用 10 块去找零,因为 5 块是粒度更小的零钱,它通用性更强,所以尽可能贪心的保存 5 块if(tens>0 && fives>0){tens--fives--}else if (tens === 0 && fives>=3){fives -=3}else{return false}}}return true};
406. 根据身高重建队列
分析
- 先分类,将身高一样的先缓存在一起
- 然后根据 key 从高到低开始贪心的排列,因为每一次我们都取
最高且前面人数最少的 item, 这个时候队列的两个条件已经一起限制好,只需要按照 item[i] 插入到 ret 上就足够了 – 后续的插入是不会影响到当前插入的,因为后续的值肯定会贴合现有排好的 ret; - 我们可以先取出身高更高的值,因为这个时候,排在它前面的,就只有它自己和已经排好的数组 – 这就是局部贪心
- 这个时候在相同身高的数组里,还要根据前面的人数进行一次排序,保证少的在前面 – 这样当前 item 插入到最终 ret 的时候,它就可以根据 item[1] 直接插入到 ret 对应的位置了
- 时间复杂度 O(n),空间复杂度 O(n)
var reconstructQueue = function(people) {const map = new Map(); // 先将身高一眼给的缓存起来for(let i = 0;i<people.length;i++){const key = people[i][0]map.set(key,map.get(key)?[...map.get(key),people[i]]:[people[i]])}const arr = [...map.keys()].sort((a,b)=>b-a) // 从大到小const ret = []for(let i = 0;i<arr.length;i++){const tempArr = map.get(arr[i]) // 取出数组tempArr.sort((a,b)=>a[1]-b[1]) // 身高相同的数组,要根据在他们前面的人的数量进行排序,这样才能保证前面人少的在前面// 这个时候需要只需要按找数组的第二个值,插入到最终数组即可for(let temp of tempArr){ret.splice(temp[1],0,temp) // 在 temp[1] 的位置插入 temp}}return ret
};const ret = reconstructQueue([[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]);
console.log(ret)
452. 用最少数量的箭引爆气球
分析 – 失败
- 首先要审题并理解题目,虽然说的是二维空间的气球,但是实际排列的时候在一个坐标 x 上可能会存在气球的重叠;所以当箭从 x 射进去,就可以一次打破 n>1 个气球
- 所以题目就转换成 – 每次找到
重叠最多的位置进行射击,当气球射完需要多少箭;-- 也就是找到交集的数量 - 这里可以和并查集进行对比,并查集遇到交集后,会扩展集合为并集,而这里是收缩到交集,所以刚好是相反的概念
- 这里用到的贪心思想就是,一旦有交集,我们就把两个气球收缩为一个更小的气球,局部贪心的将有交集的气球压缩到一个更小的气球中,这样最后剩下的气球就是相互隔离的,达到全局的贪心 – 尽可能少的射击
- 时间复杂度 O(n),空间复杂度 O(n)
- 这种写法失败的原因在于,随机找出来一个区间值,这个区间值的收缩是随机的,所以就会出现一个很小的区间 A 将本来可以容纳更多气球的某一个区间 B 收缩的很小区间 C,使得最后的结果不够贪心,而最优的情况是将区间 A 放在另外的一个区间 A1 上,然后让 B 区间容纳更多的气球 B1,B2;
- 所以需要将无序的气球按排好序,这样按顺序在局部范围内最贪心的重叠气球,就可以保证在局部范围内,尽可能小的缩小取值区间,容纳更多的气球 – 具体看
分析2
var findMinArrowShots = function(points) {const len = points.length let ret = [] // 缓存没有交集的数组for(let i =0;i<len;i++){const pp = points[i]let isMerge = falsefor(let i = 0;i<ret.length;i++){const rr = ret[i]// 如果起始位置都超过了终止位置,那么就没有交集了if(pp[0]>rr[1] || pp[1]< rr [0]) continue// 否则就是有交集了,那么只要保存交集就好,因为射中交集的时候,一次性就完成所有的气球爆炸ret[i] = pp[0]<=rr[0]?[rr[0],Math.min(pp[1],rr[1])]:[pp[0],Math.min(pp[1],rr[1])]isMerge = true // 如果合并了break}if(!isMerge){ret.push(pp)}}return ret.length
};
分析2
- 基于上面那种两边同时限制,会出现分组限制更多的情况,我们限制其中一边进行排序,尽可能使用其中一边作为限制条件,在这里我们根据 left 作为排序依据进行排序
- 排序之后,我们只需要判断新的气球的最左边是否离开了当前气球的最右边,就可以判断是否是同一组;
- 如果属于同一组,那么需要现在这一组最 right 的位置,这个位置也是射击的最右位置,保证往这个点射进去,这一组的气球全爆,所以需要找的是交集最小值
- 时间复杂度 O(nlogn), 空间复杂度 O(1)
- 这里用到的贪心思想就是尽可能局部最多重叠的气球,而上题也是因为没法保证会让最多重叠气球放在一起
var findMinArrowShots = function(points) {const len = points.length points.sort((a,b)=>a[0]-b[0])let cur = -Infinity;let ret = 0for(let i = 0 ;i<len;i++){const pp = points[i]if(pp[0]>cur) {// 超出范围了ret++cur = pp[1] // 修改}else{cur = Math.min(cur,pp[1])}}return ret
}findMinArrowShots([[10,16],[2,8],[1,6],[7,12]])
findMinArrowShots([[1,2]])
findMinArrowShots([[3,9],[7,12],[3,8],[6,8],[9,10],[2,9],[0,9],[3,9],[0,6],[2,8]])
分析3 – 右侧节点排序
- 使用左侧节点排序,在重合区域要保证 right 节点最小,这个才能保证下一个值可以落到集合的交汇处
- 但是使用右侧排序的时候,本身 right 节点就比 left 节点要大,所以右侧排序后,其他的节点对于当前节点 [l1,r1] 而言,只要 l2 < r1, 那么必然是存在于区间内的,而且只要存在于区间内,那么 right 值都不需要变,因为第一个取值就是最小了,所以有下面的写法
- 这种排序更直观一点,画图会更好看清楚
var findMinArrowShots = function(points) {const len = points.length points.sort((a,b)=>a[1]-b[1]) // 右侧排序let right = -Infinity;let ret = 0for(let i = 0 ;i<len;i++){const pp = points[i]if(pp[0]>right) {// 超出范围了ret++right = pp[1] // 修改}}return ret
}
435. 无重叠区间
分析
- 和 452. 用最少数量的箭引爆气球 类似,只是那边尽可能集合在一起,这里是要分开
- 所以这里以区间的右侧值做排序,这样 的好处就是,一旦某个值的 left 大于当前的 right 值,那么就出现完全隔离的区间了;
- 最后的答案就是长度减去可以完全隔离的区间
var eraseOverlapIntervals = function(intervals) {const length = intervals.lengthintervals.sort((a,b) => a[1]-b[1]) // 按右侧大小排列好let right = -Infinitylet ret = 0 // 集合数量for(let i = 0;i<length;i++){const ii = intervals[i]if(ii[0]>=right) {ret++ right = ii[1]}}return length-ret
}
763. 划分字母区间
分析
- 题目限制条件1:相同的字符只能存在于同一个字符串片段;限制条件2:尽可能多的切分字符串片段
- 所以我们先用 map 缓存每个字符最后出现的下标值,那么当我的字符串中存在这个字符,那么最少要走到它的尽头下标
- 相当于开启了一个不定长窗口,然后在这个窗口遍历过程,判断窗口的最长值是否需要扩展,当窗口遍历完成后,记录窗口的长度,然后执行下一个窗口
- 时间复杂度 O(n),空间复杂度 O(n)
- 这里没看出局部贪心导向全局贪心,可能是保证所有相同字符都要在一起算是局部贪心吧
var partitionLabels = function(s) {const map = new Map() // 记录字符和最后一个字符对应的下标for(let i = 0;i<s.length;i++){const ss = s[i]map.set(ss,i)}console.log(map)let ret = []let start = 0// 现在尽可能短的获取片段while(start<s.length){let temp = start // 起始值let end = map.get(s[start]) //第一个字母的最后一个下标while(start<=end){if(map.get(s[start])>end){end = map.get(s[start]) // 将 end 变长}start++}// 抛出一轮了ret.push(start-temp)}return ret
};console.log(partitionLabels('ababcbacadefegdehijhklij'))
56. 合并区间
分析
- 这里是合并所有重叠的区间,不是两两重叠的区间,所以还是得排个序,这样只需哟啊判断一遍即可,不然直接写个 ret,原来不连接的区间,可能加了一个新的 item 就连接起来了,更麻烦
- left 节点排序是比较合适的,因为这里需要在某个节点隔断之后,往后的节点不会再影响到 ret 数组里的区间
- 如果用 right 节点排序,就会出现 [k,r],[k-1,r+1] 的情况,那么已经放入到单独区域的区间还要拿出来用
- 最后遍历一遍结束,时间复杂度 O(n)
var merge = function (intervals) {intervals.sort((a, b) => a[0] - b[0]);let ret = [];let cur = intervals[0];for (let i = 1; i < intervals.length; i++) {const temp = intervals[i];if (temp[0] > cur[1]) {// 当取出的空间的起始值已经比当前值要大的时候,那么剩下的其他值,也会完全和当前的 cur 隔离开,所以将当前 cur 推入 ret 中ret.push(cur);cur = temp; // 替换 cur}if (cur[1] < temp[1]) {cur[1] = temp[1];}}return [...ret, cur];
};console.log(merge([[1,4],[2,3]])
);
738. 单调递增的数字
分析
- 审题,这里是要找一个最大的数 num,num 的位需要单增,也就是 1234,这样的,同时 num <= n
- 这题数字转字符串转数组,将每个值转成单个数值来计算了,这样更方便点
- 这里最后要求的是递增的数组,所以我们可以根据 i-1 和 i 之间的值进行替换,当 arr[i-1]>arr[i] 的时候, arr[i-1] 减一,设置锚点 flag
- 从后往前遍历完之后,找到左侧第一个需要设置为9的点,然后把后面的值全设置为9,达到最大值
var monotoneIncreasingDigits = function (n) {if(n<10) return n //如果是个位数,直接返回 nconst str = String(n)const len = str.lengthconst arr = str.split('')let flag = Infinity // 标记最后一个设置为 9 的下标,从这个下标之后的值,都得换成 9for(let i =len-1;i>=0;i--){if(arr[i-1]>arr[i]){// 如果前一位大于后一位,那么为了当增,需要将当前位减一,后一位换成 9flag = iarr[i-1] = arr[i-1] -1 }}for (let i = flag; i < len; i++) {arr[i] = 9}return Number(arr.join(''))
};
968. 监控二叉树
分析
- 这里要求尽可能少的安装摄像头,但是改装的还是得装上,需要全覆盖,那么最好的办法肯定是自底向上的装,因为层数越深,节点越多,所以自顶向上能减少摄像头的安装
- 那么现在要尽可能让摄像头覆盖到每一个节点,这里节点 val 作为状态值,0就是没有覆盖,1就是安装摄像头覆盖,2是没有安装但是在覆盖范围内
- 我们知道要尽可能的在有状态为 0 的叶子节点的
父节点上去安装,这样就可以一次性覆盖到叶子节点,同时由于是自底向上的遍历,那么不需要考虑更底层的覆盖,只需要考虑当前节点和它的叶子节点即可 - 所以我们用后续遍历的方式进行后续遍历,当我们到达叶子节点时返回;
- 当我们遇到叶子节点都为不为 0,也就是都在覆盖范围内的时候,如果存在叶子节点状态为 1,即当前节点也属于覆盖范围,需要更改状态为 2, 然后 return 回去 – 这里用到了贪心,也就是必须要有状态为 0 的叶子节点,才会去安装摄像头,保证摄像头的覆盖范围,进而保证数量最小
- 如果存在叶子节点的状态为 0,那么就必须在当前节点设置摄像头,也就将状态 root.val 设置为 1
- 当我们自低向上遍历到了根节点,然后中断遍历的时候,还需要考虑最后 root 节点
- 因为我们之前的逻辑是根据叶子节点状态来判断当前节点的更改的,所以 root 节点很可能会因为叶子节点是覆盖值而没有进行任何的设置,这个时候 root 就可能是 0,所以如果 root 是 0 的话,还得再安一个摄像头
- 我们最终的结果就是要保证整棵树的节点状态都不为 0即可
- 时间复杂度 O(n)
var minCameraCover = function (root) {if (!root) return 0;let ret = 0; // 装了多少摄像头const dfs = (root) => {if (!root.left && !root.right) return; // 到达叶子节点,直接返回,不加摄像头if (root.left) dfs(root.left);if (root.right) dfs(root.right);// 后序遍历,遇到父子节点存在摄像头,那就不需要加了if ((root.left && root.left.val !== 0 || !root.left) && (root.right && root.right.val !== 0 || !root.right)){if((root.left && root.left.val === 1) || (root.right && root.right.val === 1)){// 存在摄像头才能波及root.val = 2 // 波及到的}return }// 必须要保证存在的子节点都已经是 1 的时候,才可以放心继续往上走root.val = 1; //如果大家伙都没有装,那就我来装吧ret++;};dfs(root);return root.val === 0 ? ret+1 : ret
};
相关文章:

JavaScript刷LeetCode拿offer-贪心算法
前言 学习算法的时候,总会有一些让人生畏的名词,比方动态规划,贪心算法 等,听着就很难;而这一 part 就是为了攻破之前一直没有系统学习的 贪心算法; 有一说一,做了这些贪心题,其实…...

selenium
下载并安装selenium 安装:cmd中执行 pip install -i https://pypi.douban.com/simple selenium执行完成后 pip show selenium 可查看安装是否成功安装浏览器驱动,查看当前浏览器的版本选择合适的驱动并下载 chrome的链接:https://chromedrive…...

SpringMVC的视图
转发视图ThymeleafView若使用的视图技术为Thymeleaf,在SpringMVC的配置文件中配置了Thymeleaf的视图解析器,由此视图解析器解析之后所得到的是ThymeleafView。解析:当控制器方法中所设置的视图名称没有任何前缀时,此时的视图名称会…...
idea使用本地代码远程调试线上运行代码---windows环境
场景: 今天在书上看了一个代码远程调试的方法,自己本地验证了一下感觉十分不错!! windows环境: 启动测试jar包:platform-multiappcenter-base-app-1.0.0-SNAPSHOT.jar 测试工具:postman,idea 应…...
简单记录简单记录
目录1.注册Gmail2.注册ChatGPT3.验证“真人”使用4.开始使用1.注册Gmail 第一步先注册一个谷歌邮箱,你也可以使用微软账号,大部分人选择使用gmail。 申请谷歌邮箱 选择个人用途创建账号即可。 📌温馨提示: 你直接使用guo内的网…...
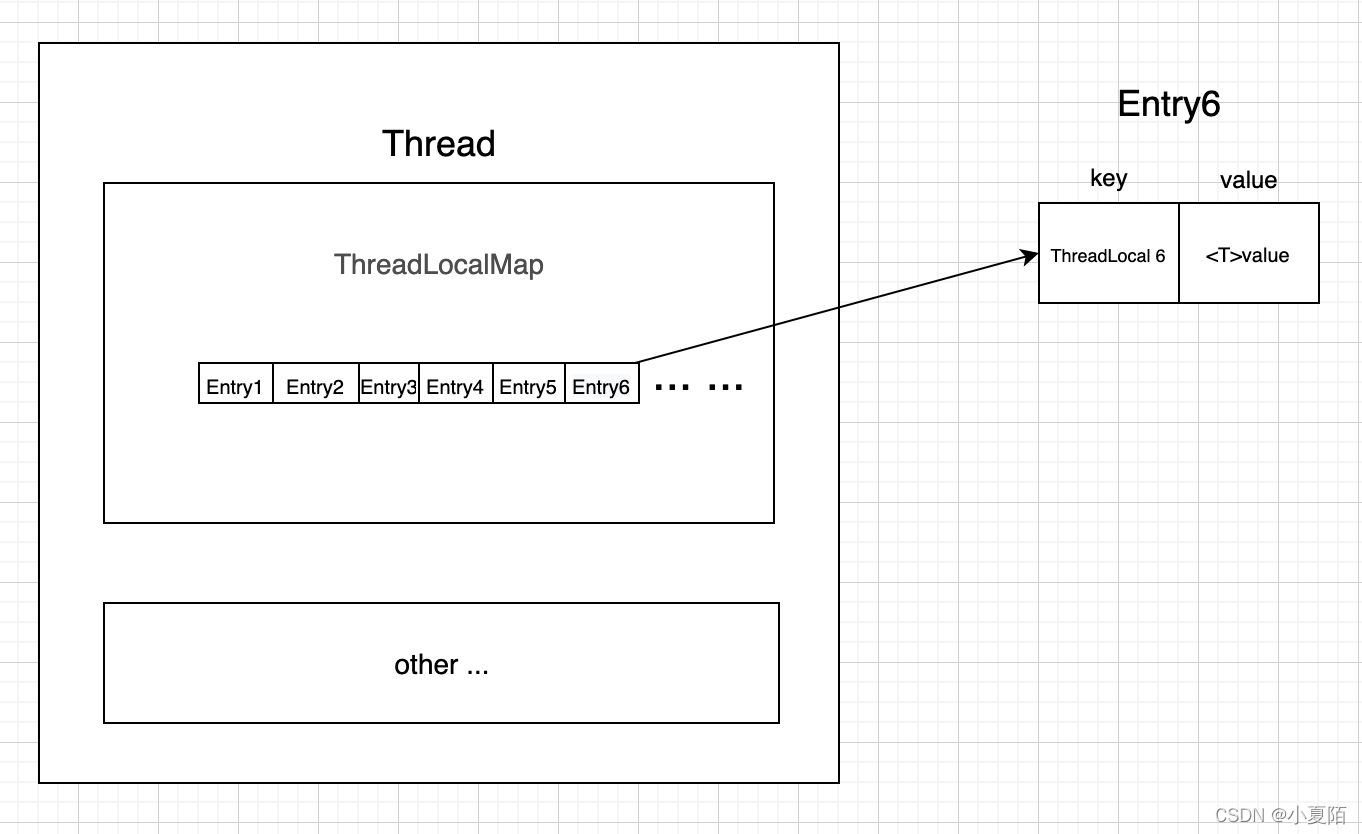
源码系列 之 ThreadLocal
简介 ThreadLocal的作用是做数据隔离,存储的变量只属于当前线程,相当于当前线程的局部变量,多线程环境下,不会被别的线程访问与修改。常用于存储线程私有成员变量、上下文,和用于同一线程,不同层级方法间传…...
——特点及关键字)
C语言入门(1)——特点及关键字
1、C特点及与Java区别 1.1、C特点 面向过程 一般用于嵌入式开发、编写最底层的程序、操作系统 可以直接操作内存 可以封装动态库 不容易跨平台 有指针 可以直接操作串口 线程更加灵活 和硬件打交道速度是最快的 1.2、和Java区别 C是C的增强版,增加了一些新的特性&…...

react中useEffect和useLayoutEffect的区别
布局上 useEffect在浏览器渲染完成后执行useLayoutEffect在DOM更新后执行 特点 useLayoutEffect 总是比 useEffect 先执行;useLayoutEffect与componentDidMount、componentDidUpdate调用时机相同,都是在DOM更新后,页面渲染前调用࿱…...

NoSQL(非关系型数据库)与SQL(关系型数据库)的差别
目录 NoSQL(非关系型数据库)与SQL(关系型数据库)的差别 1.数据结构:结构化与非结构化 2.数据关联:关联性与非关联性 3.查询方式:SQL查询与非SQL查询 4.事务特性:ACID与BASE 分析ACID与BASE的含义: 5.存储方式&am…...

new bing的申请与使用教程
文章目录新必应申请新必应免代使用教程总结新必应申请 下载安装 Edge dev 版本,这个版本可以直接使用 对于没有更新的用户而言,不容易找到入口,所以我们直接使用 集成new bing的dev版本 Edge dev 下载链接:https://www.microso…...

yaml配置文件
最近在写代码,发现随着网络的增加,代码变得越来越冗余,所以就想着写一个网络的配置文件,把网络的配置放到一个文件中,而不再主函数中,这样代码开起来就好看了,调试的时候也方便了。之前写过一篇…...

284. 顶端迭代器
请你在设计一个迭代器,在集成现有迭代器拥有的 hasNext 和 next 操作的基础上,还额外支持 peek 操作。 实现 PeekingIterator 类: PeekingIterator(Iterator nums) 使用指定整数迭代器 nums 初始化迭代器。 int next() 返回数组中的下一个元…...

自学前端最容易犯的10个的错误,入门学前端快来看看
在前端学习过程中,有很多常见的误区,包括过度关注框架和库、缺乏实践、忽视算法和数据结构、忽视浏览器兼容性、缺乏团队合作经验、忽视可访问性、重构次数过多、没有关注性能、缺乏设计知识以及没有持续学习等。要避免这些误区,应该注重基础…...
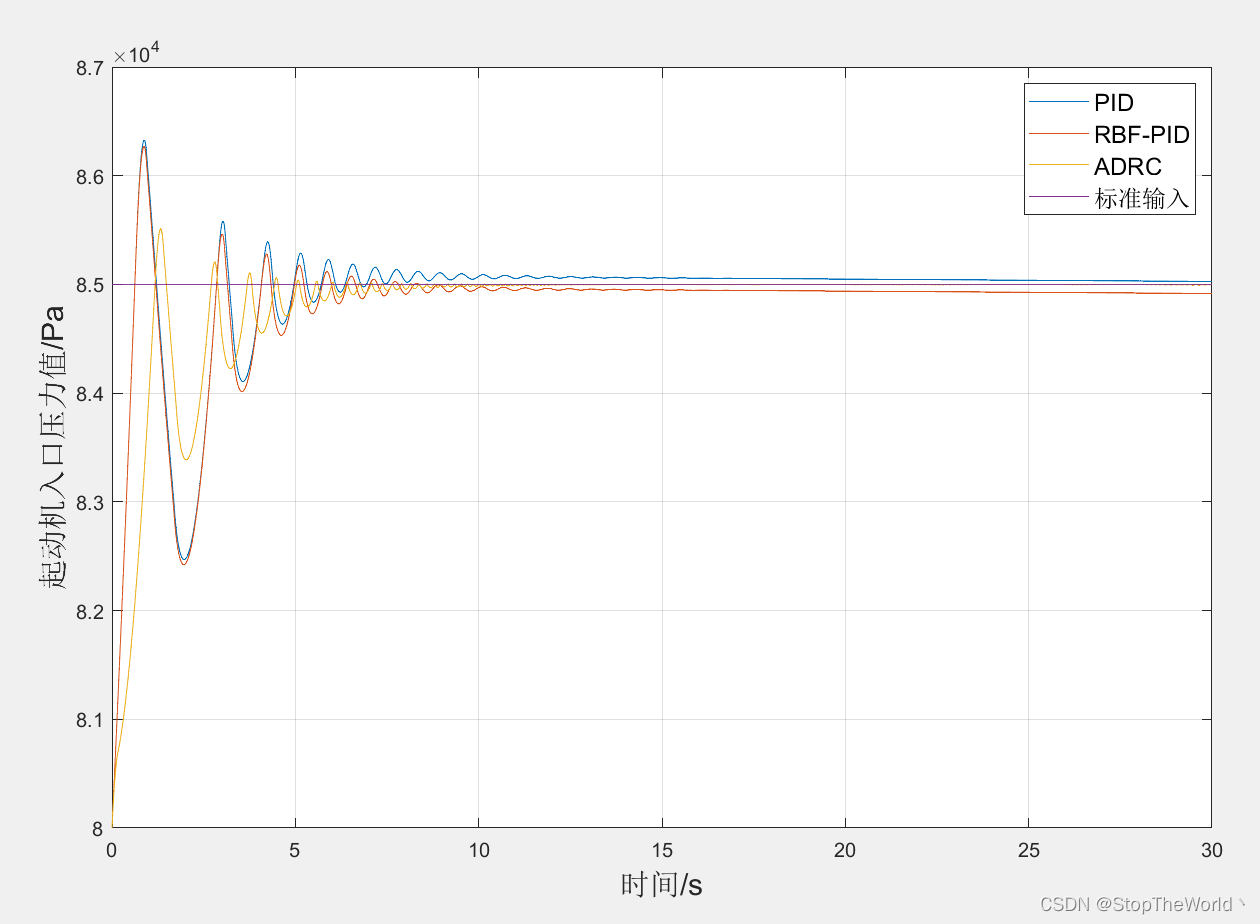
【ADRC控制】使用自抗扰控制器调节起动机入口压力值
以前只知道工业控制中用的是PID控制,然而最近了解到实际生产中还在使用ADRC控制,而且使用效果还优于PID控制,遂找了几篇文献学习学习。 0 引言 自抗扰控制(Active Disturbances Rejection Controller,ADRC)…...
)
剑指 Offer Day2——链表(简单)
目录剑指 Offer 06. 从尾到头打印链表剑指 Offer 24. 反转链表剑指 Offer 35. 复杂链表的复制剑指 Offer 06. 从尾到头打印链表 原题链接:06. 从尾到头打印链表 最容易想到的思路就是先从头到尾打印下来,然后 reverse 一下,但这里我们使用递归…...

Final Cut Pro 10.6.5
软件介绍Final Cut Pro 10.6.5 已通过小编安装运行测试 100%可以使用。Final Cut Pro 10.6.5 破解版启用了全新的矩形图标,与最新的macOS Ventura设计风格统一,支持最新的macOS 13 文图拉系统,支持Apple M1/M2芯片。经过完整而彻底的重新设计…...
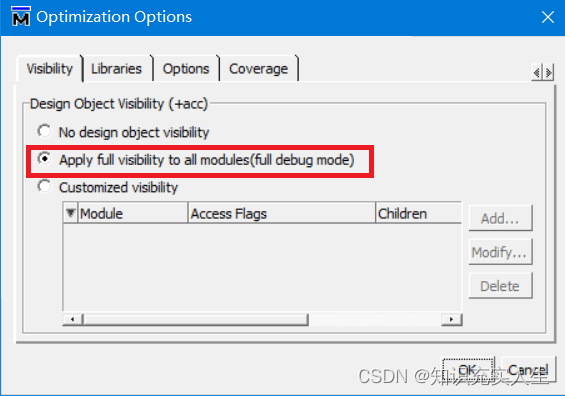
Modelsim仿真操作指导
目录 一、前言 二、仿真分类 三、RTL级仿真 3.1创建库 3.2 仿真配置设置 3.3 运行仿真 四、常见问题 4.1 运行仿真时报错“cant read "Startup(-L)": no such element in array” 4.2 运行仿真时无任何报错,但object窗口为空,可正常运…...

你知道这20个数组方法是怎么实现的吗?
前言你们一定对JavaScript中的数组很熟悉,我们每天都会用到它的各种方法,比如push、pop、forEach、map……等等。但是仅仅使用它就足够了吗?如此出色,您一定不想停在这里。我想和你一起挑战实现20数组方法的功能。1、forEachforEa…...

《系统架构设计》-01-架构和架构师概述
文章目录1. 架构的基本定义1.1 架构组成理论1.1.1 系统元素1)概念2)静态结构和动态结构1.1.2 基本系统属性1.1.3 设计和发展原则1.2 架构的决策理论1.2.1 统一软件过程(Rational Unified Process,统一软件过程)1.2.2 决…...
第七届蓝桥杯省赛——5分小组
题目:9名运动员参加比赛,需要分3组进行预赛。有哪些分组的方案呢?我们标记运动员为 A,B,C,... I下面的程序列出了所有的分组方法。该程序的正常输出为:ABC DEF GHIABC DEG FHIABC DEH FGIABC DEI FGHABC DFG EHIABC DFH EGIABC DF…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...
