【每日一题Day118】LC1124表现良好的最长时间段 | 前缀和+单调栈/哈希表
表现良好的最长时间段【LC1124】
给你一份工作时间表
hours,上面记录着某一位员工每天的工作小时数。我们认为当员工一天中的工作小时数大于
8小时的时候,那么这一天就是「劳累的一天」。所谓「表现良好的时间段」,意味在这段时间内,「劳累的天数」是严格 大于「不劳累的天数」。
请你返回「表现良好时间段」的最大长度。
下文为自己的题解总结,参考其他题解写成,取其精华,做以笔记,如有描述不清楚或者错误麻烦指正,不胜感激,不喜勿喷!
2023/2/14
看了提示还是只能双层循环 哎…
-
思路:
- 首先构造新的数组及其前缀和数组,新数组中将工作时长大于8的记为1,工作时长小于等于8的记为-1,并求出它的前缀和数组,那么题意可以转化为⌈\lceil⌈和严格大于0的连续子数组的最大长度⌋\rfloor⌋
- 那么可以通过三种方法求出⌈\lceil⌈和严格大于0的连续子数组的最大长度⌋\rfloor⌋
- 暴力
- 哈希表
- 单调栈
-
实现:暴力
class Solution {public int longestWPI(int[] hours) {int n = hours.length;int[] preSum = new int[n + 1];int res = 0;for (int i = 0; i < n; i++){ preSum[i + 1] = hours[i] > 8 ? preSum[i] + 1 : preSum[i] - 1; }for (int i = 0; i < n; i++){for (int j = i + 1; j <= n; j++){if (preSum[j] - preSum[i] > 0){res = Math.max(res, j - i);}}}return res;} }-
复杂度
- 时间复杂度:O(n2)O(n^2)O(n2)
- 空间复杂度:O(n)O(n)O(n)
-
-
实现:哈希表
- 由于新数组中的值只存在1和-1,因此相邻前缀和的差恰好为1
- 利用前缀和数组的性质可得
- 当preSum[i]>0preSum[i]>0preSum[i]>0时,最远的左端点即为j=0j= 0j=0
- 当preSum[i]<=0preSum[i]<=0preSum[i]<=0时,最远的左端点即为jjj为preSum[i]−1preSum[i]-1preSum[i]−1首次出现的位置
- 实现时,使用变量代替前缀和数组
class Solution {public int longestWPI(int[] hours) {int n = hours.length;int preSum = 0;Map<Integer, Integer> map = new HashMap<>();int res = 0;for (int i = 0; i < n; i++){ preSum += hours[i] > 8 ? 1 : -1; if (preSum > 0){res = Math.max(res, i + 1);}else if (map.containsKey(preSum - 1)){res = Math.max(i - map.get(preSum - 1), res);}if (!map.containsKey(preSum)){map.put(preSum, i);}}return res;} }class Solution {public int longestWPI(int[] hours) {int n = hours.length, ans = 0, s = 0;var pos = new int[n + 2]; // 记录前缀和首次出现的位置for (int i = 1; i <= n; ++i) {s -= hours[i - 1] > 8 ? 1 : -1; // 取反,改为减法if (s < 0) ans = i;else {if (pos[s + 1] > 0) ans = Math.max(ans, i - pos[s + 1]);if (pos[s] == 0) pos[s] = i;}}return ans;} }作者:灵茶山艾府 链接:https://leetcode.cn/problems/longest-well-performing-interval/solutions/2110211/liang-chong-zuo-fa-liang-zhang-tu-miao-d-hysl/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。- 复杂度
- 时间复杂度:O(n)O(n)O(n)
- 空间复杂度:O(n)O(n)O(n)
-
实现:单调栈
- 当s[j]<s[i]s[j] < s[i]s[j]<s[i]时,jjj可以作为左端点,而我们要求最大长度,因此应该尽可能让jjj位于左端点,因此可以使用单调递减栈存放
preSum中递减元素的下标 - 而如果存在s[r1]<s[r2],r1<r2s[r_1]<s[r_2],r_1<r_2s[r1]<s[r2],r1<r2的情况时,r1r_1r1一定不是最远的右端点,因为存在一个左端点满足s[l]<s[r1]<s[r2],l<r1<r2s[l]<s[r_1]<s[r_2],l<r_1<r_2s[l]<s[r1]<s[r2],l<r1<r2,那么此时最长子数组区间为[l,r2][l,r_2][l,r2],因此为了避免再次将元素放入栈中,我们可以选择倒序遍历右端点
class Solution {public int longestWPI(int[] hours) {int n = hours.length, ans = 0;var s = new int[n + 1]; // 前缀和var st = new ArrayDeque<Integer>();st.push(0); // s[0]for (int j = 1; j <= n; ++j) {s[j] = s[j - 1] + (hours[j - 1] > 8 ? 1 : -1);if (s[j] < s[st.peek()]) st.push(j); // 感兴趣的 j}for (int i = n; i > 0; --i)while (!st.isEmpty() && s[i] > s[st.peek()])ans = Math.max(ans, i - st.pop()); // [栈顶,i) 可能是最长子数组return ans;} }作者:灵茶山艾府 链接:https://leetcode.cn/problems/longest-well-performing-interval/solutions/2110211/liang-chong-zuo-fa-liang-zhang-tu-miao-d-hysl/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。- 复杂度
- 时间复杂度:O(n)O(n)O(n)
- 空间复杂度:O(n)O(n)O(n)
- 当s[j]<s[i]s[j] < s[i]s[j]<s[i]时,jjj可以作为左端点,而我们要求最大长度,因此应该尽可能让jjj位于左端点,因此可以使用单调递减栈存放
相关文章:

【每日一题Day118】LC1124表现良好的最长时间段 | 前缀和+单调栈/哈希表
表现良好的最长时间段【LC1124】 给你一份工作时间表 hours,上面记录着某一位员工每天的工作小时数。 我们认为当员工一天中的工作小时数大于 8 小时的时候,那么这一天就是「劳累的一天」。 所谓「表现良好的时间段」,意味在这段时间内&#…...
)
vue使用nprogress(进度条)
目录 1.安装 2.引入 3.配置 4.使用 5.使用场景 6.改变颜色 1.安装 npm install --save nprogress2.引入 import NProgress from nprogress import nprogress/nprogress.css3.配置 NProgress.configure({easing: ease, // 动画方式,和css动画属性一样&#…...

@NotNull 、@NotBlank、@NotEmpty区别和使用
引言 今天在使用validation校验的时候,发现了使用校验不起作用,一时间有点摸不到头绪,就看了一下同事提交的代码,发现了问题在用NotNull用法,用的有些错误,所以在这里讲一下NotNull、NotBlank、NotEmpty区…...
Nacos——Nacos简介以及Nacos Server安装
资料来源:02-Nacos配置管理-什么是配置中心_哔哩哔哩_bilibili nacos记得下载2.x版本的,负责以后新建配置的时候会出现“发布错误,请检查参数是否正确”错误!!!! 目录 一、Nacos简介 1.1 四…...

Presto 文档和笔记
1. Presto Presto 官网 Presto 文档 2. 配置 3.1 node 配置 cat etc/node.properties # Generated by Apache Ambari. Fri Feb 10 14:52:10 2023node.data-dir/mnt/bmr/presto/data node.environmentproduction node.idbmr-master-4b7cbaa3.2 jvm 配置 cat etc/jvm.confi…...
大尺度衰落与小尺度衰落
一. 大尺度衰落 无线电磁波信号在收发天线长距离(远大于传输波长)或长时间范围发生的功率变化,称为大尺度衰落,一般可以用路径损耗模型来描述,路径损耗是由发射功率在空间中的辐射扩散造成的,根据功率传输…...
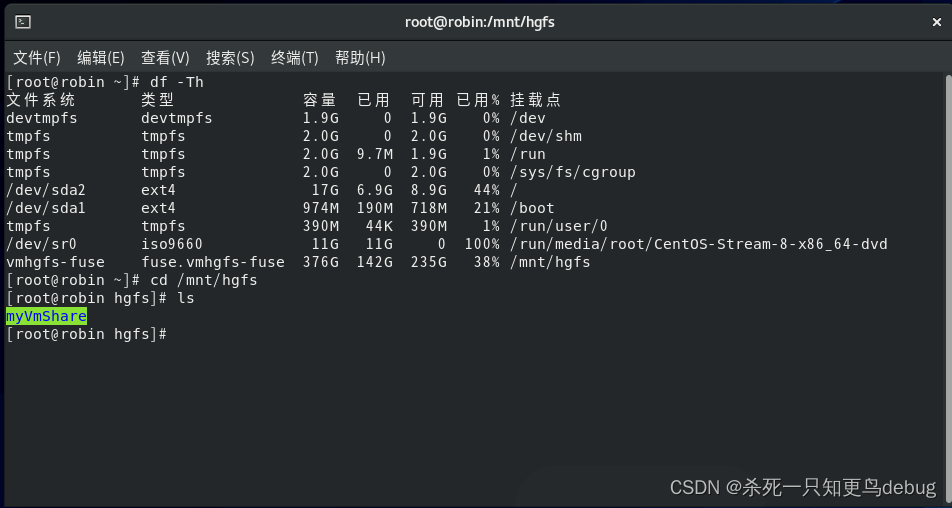
完美解决:重新安装VMware Tools灰色。以及共享文件夹的创建(centos8)
解决:重新安装VMware Tools灰色问题:重新安装VMware Tools灰色解决方案-挂载VMware中的linux.iso1. vmtools的linux.iso挂载及安装2. 共享文件夹的创建及配置问题:重新安装VMware Tools灰色 发现一个小问题,我的vm虚拟机安装后发…...

达梦数据库作业管理
一、基本功能 作业系统大致包含作业,警报,操作员三部分。 作业可运行DMPL/SQL脚本,定期备份数据库,检查等。可定时执行,也可通过警报触发执行,可产生警报通知用户状态。一个作业由多个步骤组成,…...

数据结构-考研难点代码突破(C++实现树型查找-二叉搜索树(二叉排序树))
文章目录1.二叉搜索树基本操作二叉搜索树的效率分析2. C实现1.二叉搜索树基本操作 二叉排序树是具有下列特性的二叉树: 若左子树非空,则左子树上所有结点的值均小于根结点的值。若右子树非空,则右子树上所有结点的值均大于根结点的值。左、…...

emqx异常处理
启动异常 通过解压tar压缩包安装后通过 ./bin/emqx start 启动报错 WARNING: Default (insecure) Erlang cookie is in use. WARNING: Configure node.cookie in /opt/emqx/etc/emqx.conf or override from environment variable EMQX_NODE__COOKIE NOTE: Use the same config…...

Web前端:开始学习ReactJS需要知道什么?
毫无疑问,ReactJS是前端开发者中最著名的库之一,它的受欢迎程度与日俱增。用ReactJS构建的网站看起来非常棒,大多数开发新手都被它吸引住了。然而,许多新人和有经验的开发人员在没有首先了解先决条件的情况下,就直接用…...

卡诺图化简
1.相关概念 最小项:函数的某个乘积项包含了函数的全部变量(原变量或反变量的形式),且每个变量仅出现一次,则这个乘积项为该函数的一个标准积项。 最小项中的原变量记为1,反变量记为0,当变量顺序…...
带你了解软件测试是做什么的
软件测试是互联网技术中一门重要的学科,它是软件生命周期中不可或缺的一个环节,担负着把控、监督软件的质量的重任。 人才稀缺,对于求职者来说就意味着机会。但是很多想学习软件测试的人对这个学科并不了解,也不知道该如何学习&a…...
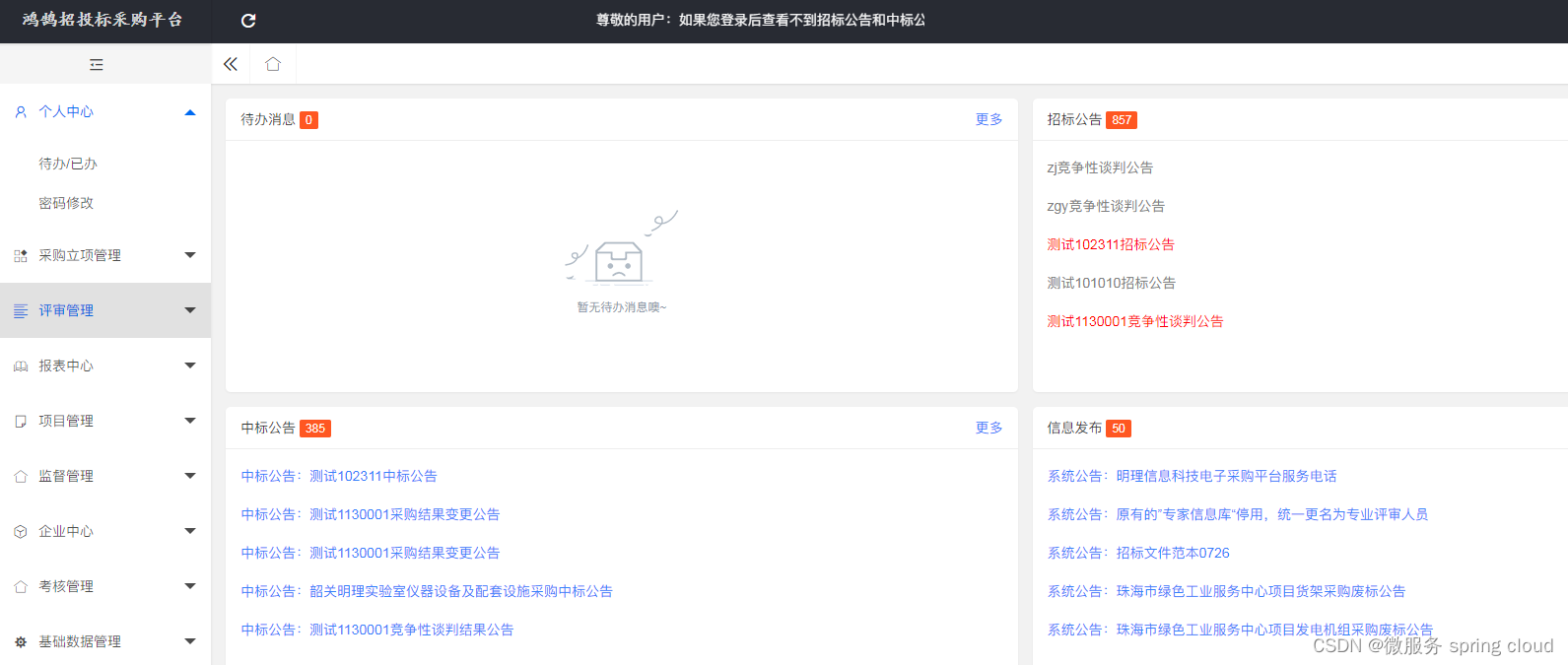
企业电子招投标采购系统源码之功能模块功能描述
功能模块: 待办消息,招标公告,中标公告,信息发布 描述: 全过程数字化采购管理,打造从供应商管理到采购招投标、采购合同、采购执行的全过程数字化管理。通供应商门户具备内外协同的能力,为外…...

职场中的高手,是如何高质量解决问题?
职场总会遇见很多新问题,高手会从容应对,因为他们学习了一套通 用理论,可以处理工作当中的大部分内容,剩下的一部分能够用快速 提问的方式找到思路。 记得几年前有个同事 A,下午四点多项目突然丢过来一个活,…...
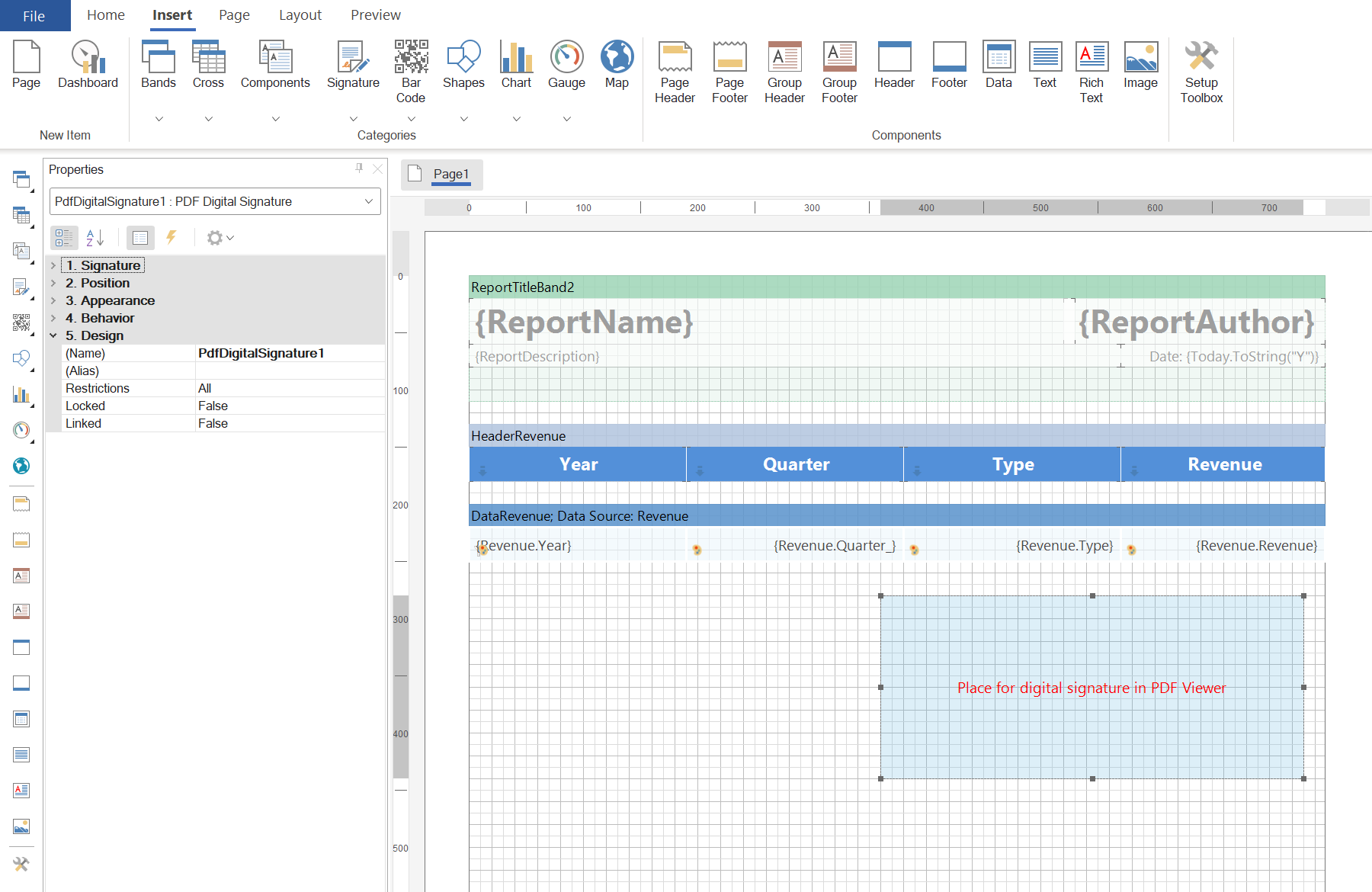
报表生成工具Stimulsoft中的电子签名和 PDF 数字签名
Stimulsoft Reports 是一款报告编写器,主要用于在桌面和Web上从头开始创建任何复杂的报告。可以在大多数平台上轻松实现部署,如ASP.NET, WinForms, .NET Core, JavaScript, WPF, Angular, Blazor, PHP, Java等,在你的应用程序中嵌入报告设计器…...
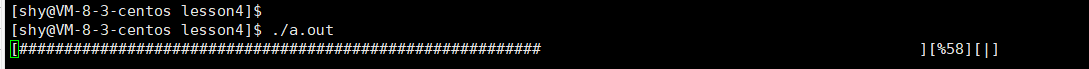
【Hello Linux】Linux环境下写的第一个程序 -- 进度条
作者:小萌新 专栏:Linux 作者简介:大二学生 希望能和大家一起进步! 本篇博客简介:写出Linux中的第一个小程序 进度条 进度条小程序行缓冲区概念\r 和 \n进度条代码和演示行缓冲区概念 我们首先用两段代码来感受下行缓…...

【基础】性能测试,从0到实战(手把手教,非常实用)
一、性能基础 什么是性能测试--->本质? 基于协议来模拟用户发送的请求(业务模拟),对服务器形成一定负载。关注点:时间性能、空间性能与界面无关 性能测试分类 性能测试(狭义) 性能测试方法是通过模…...
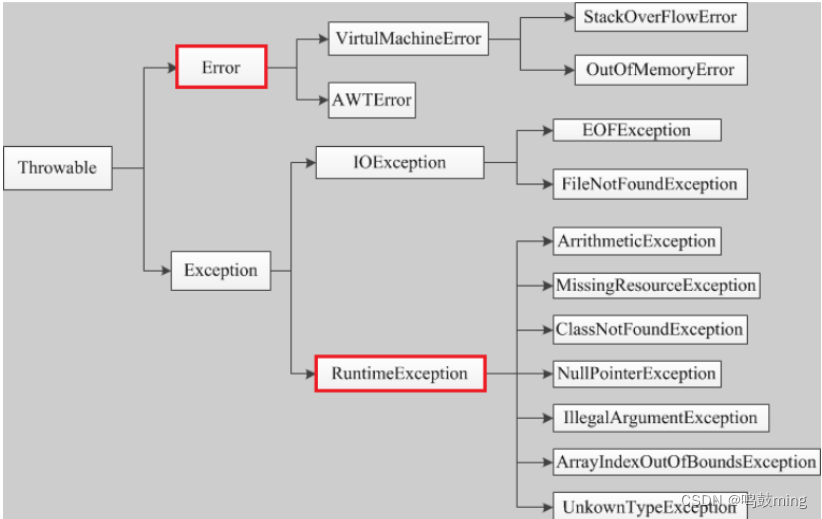
07-Java异常分类以及处理机制
1.异常概念 Java标准库内建了一些通用的异常,这些类以Throwable为顶层父类。Throwable又派生出Error类和Exception类。 1.错误:是程序无法处理的错误,表示运行应用程序中较严重问题。大多数错误与代码编写者执行的操作无关,而表示…...

用到的C++的相关知识-----未完待续
文章目录前言一、vector函数的使用1.1 构造向量二、常用函数2.1 矩阵输出函数2.2 向量输出函数2.3 矩阵的使用2.4三、new的用法3.1 内存的四种分区3.2 new的作用3.33.4四、4.14.24.34.4总结前言 只是为方便学习,不做其他用途 一、vector函数的使用 有关的文章 C v…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...
