数据结构-考研难点代码突破(C++实现树型查找-二叉搜索树(二叉排序树))
文章目录
- 1.二叉搜索树基本操作
- 二叉搜索树的效率分析
- 2. C++实现
1.二叉搜索树基本操作
二叉排序树是具有下列特性的二叉树:
- 若左子树非空,则左子树上所有结点的值均小于根结点的值。
- 若右子树非空,则右子树上所有结点的值均大于根结点的值。
- 左、右子树也分别是一棵二叉排序树
根据二叉排序树的定义,左子树结点值< 根结点值< 右子树结点值。
所以对二叉排序树进行中序遍历,可以得到一个递增的有序序列。
二叉排序树的搜索:
- 从根结点开始,沿某个分支逐层向下比较的过程。
- 若二叉排序树非空,先将给定值与根结点的关键字比较,若相等,则查找成功
- 若不等,如果小于根结点的关键字,则在根结点的左子树上查找,否则在根结点的右子树上查找。
这个过程可以通过递归或者非递归实现实现
二叉排序树的插入:
- 若原二叉排序树为空,则直接插入结点
- 若关键字k小于根结点值,则插入到左子树,若关键字k大于根结点值,则插入到右子树。
插入的结点一定是一个新添加的叶结点,且是查找失败时的查找路径上访问的最后一个结点的左孩子或右孩子.
二叉排序树的删除
在二叉排序树中删除一个结点时,不能把以该结点为根的子树上的结点都删除,必须先把被删除结点从存储二叉排序树的链表上摘下,将因删除结点而断开的二叉链表重新链接起来,同时确保二叉排序树的性质不会丢失。删除操作的实现过程按3种情况来处理
-
若被删除结点z是叶结点,则直接删除,不会破坏二叉排序树的性质
-
若结点z只有一棵左子树或右子树,则让z的子树成为z父结点的子树,替代z的位置
-
若结点z有左、右两棵子树,则令z的直接后继(或直接前驱)替代z,然后从二叉排序树中删去这个直接后继(或直接前驱),这样就转换成了第一或第二种情况。可以使用递归解决这个问题。
直接后继:节点右子树中最左节点(右子树最小节点)
删除流程图:具体看代码流程
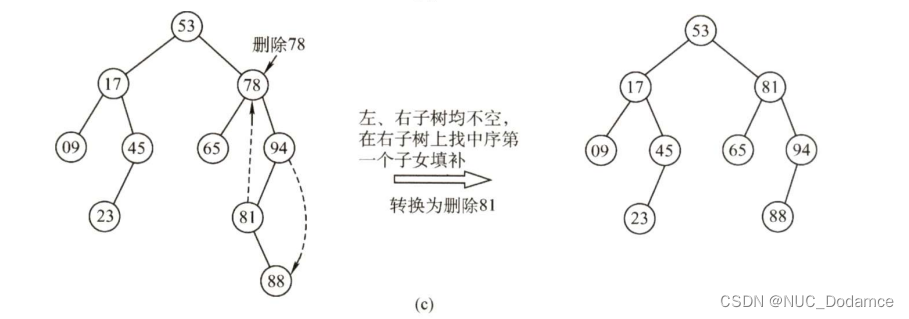
二叉搜索树的效率分析
二叉排序树的查找效率,主要取决于树的高度。
-
若二叉排序树的左、右子树的高度之差的绝对值不超过1(这样的二叉排序树称为平衡二叉树)它的平均查找长度为O(logN)
-
若二叉排序树是一个只有右(左)孩子的单支树(类似于有序的单链表),则其平均查找长度为O(N)
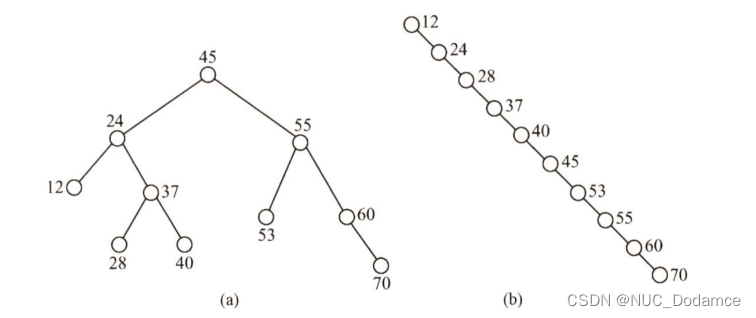
a图的平均搜索成功长度ASL:类似折半查找(1x1 + 2x2+……h×2h-1) )(每层的节点不一定放满,需要针对题目灵活处理)
(1×1+2×2+3×4+4×3)÷10=2.9
b图的平均搜索成功长度ASL:(1+10)/2=5.5
因为此时搜索二叉树由树型退化为线型,平均搜索长度为(n+1)/2
二叉排序树与二分查找相似。就平均时间性能而言,二叉排序树上的查找和二分查找差不多。
但二分查找的判定树唯一,而二叉排序树的查找不唯一,相同的关键字其插入顺序不同可能生成不同的二叉排序树。
二叉排序树与二分搜索:
- 二叉排序树无须移动结点,只需修改指针即可完成插入和删除操作, 平均执行时间为O(logN)
- 二分查找的对象是有序顺序表,若有插入和删除结点的操作,所花的代价是O(n)。
- 当有序表是静态查找表时,宜用顺序表作为其存储结构,采用二分查找实现其查找操作;若有序表是动态查找表,则应选择二叉排序树作为其逻辑结构.
2. C++实现
// 二叉搜索树头文件实现
#include <iostream>
#include <vector>
#include <algorithm>struct TreeNode
{int _val;TreeNode *_left;TreeNode *_right;TreeNode(int val) : _val(val), _left(nullptr), _right(nullptr) {}
};class SearchTree
{
private:TreeNode *root = nullptr;/*** @brief 在二叉搜索树中查找节点值为val的节点** @param val 查找节点的值* @param node 如果找到了这个节点,node就是这个节点的地址,否则为null* @param part part这个节点的父亲,如果这个节点为null,这个参数输出null*/void _find(int val, TreeNode *&node, TreeNode *&part){TreeNode *ptr = root;TreeNode *prev = nullptr;while (ptr != nullptr){if (ptr->_val == val){node = ptr;break;}else if (ptr->_val > val){prev = ptr;ptr = ptr->_left;}else{prev = ptr;ptr = ptr->_right;}}node = ptr;part = prev;}bool _erase(int val, TreeNode *&node){if (node == nullptr){return false;}else{if (node->_val > val){_erase(val, node->_left);}else if (node->_val < val){_erase(val, node->_right);}else{if (node->_left == nullptr){TreeNode *del = node;node = node->_right;delete del;}else if (node->_right == nullptr){TreeNode *del = node;node = node->_left;delete del;}else{// 找要删除节点的后继TreeNode *right_min_node = node->_right;while (right_min_node->_left != nullptr){right_min_node = right_min_node->_left;}// 记录right_min_node这个节点的值,吧这个节点的值和node节点交换,在删除right_min_node这个节点即可// right_min_node这个节点的左子树一定为空,在上面顶点流程会处理int tmp = right_min_node->_val;_erase(tmp, node->_right);node->_val = tmp;}}return true;}}// 判断一棵树是否是二叉搜索树,检查每个节点是否满足节点值的取值范围bool _isSearchTree(TreeNode *node, int min, int max){if (node == nullptr)return true;if (node->_val < min || node->_val > max){return false;}return _isSearchTree(node->_left, min, node->_val - 1) && _isSearchTree(node->_right, node->_val + 1, max);}void _display_inorder(TreeNode *node){if (node == nullptr)return;_display_inorder(node->_left);std::cout << node->_val << " ";_display_inorder(node->_right);}int _max(){TreeNode *node = root;while (node->_right != nullptr){node = node->_right;}return node->_val;}int _min(){TreeNode *node = root;while (node->_left != nullptr){node = node->_left;}return node->_val;}public:SearchTree() = default;SearchTree(const std::vector<int> &buff){for (int i = 0; i < buff.size(); i++){insert(buff[i]);}}// 不允许重复插入相同的值bool insert(int val){if (root == nullptr){root = new TreeNode(val);return true;}else{TreeNode *pos = nullptr;TreeNode *prev = nullptr;_find(val, pos, prev);if (pos != nullptr){// 之前插入过,值重复return false;}else{// pos==nullptr;if (prev->_val > val){prev->_left = new TreeNode(val);}else{prev->_right = new TreeNode(val);}return true;}}}// 查找节点值为val的节点bool find(int val){TreeNode *node;TreeNode *part;_find(val, node, part);return node != nullptr;}// 删除搜索二叉树节点bool erase(int val){return _erase(val, root);}// 判断这颗树是否为二叉搜索树bool isSearchTree(){return _isSearchTree(root, _min(), _max());}// 中序遍历二叉搜索树void inorder(){_display_inorder(root);std::cout << "\n";}
};
测试代码:
#include "SearchTree.h"
#include <time.h>using namespace std;#define TIMES 10int main(int argc, char const *argv[])
{srand((unsigned int)time(0));// vector<int> ret = {1, 2, 3};vector<int> ret;for (int i = 0; i < TIMES; i++){ret.push_back(rand() % 100);}SearchTree tree(ret);tree.inorder();tree.insert(40);tree.inorder();cout << tree.isSearchTree() << endl;tree.insert(1);tree.erase(40);tree.inorder();cout << tree.isSearchTree() << endl;return 0;
}

相关文章:

数据结构-考研难点代码突破(C++实现树型查找-二叉搜索树(二叉排序树))
文章目录1.二叉搜索树基本操作二叉搜索树的效率分析2. C实现1.二叉搜索树基本操作 二叉排序树是具有下列特性的二叉树: 若左子树非空,则左子树上所有结点的值均小于根结点的值。若右子树非空,则右子树上所有结点的值均大于根结点的值。左、…...

emqx异常处理
启动异常 通过解压tar压缩包安装后通过 ./bin/emqx start 启动报错 WARNING: Default (insecure) Erlang cookie is in use. WARNING: Configure node.cookie in /opt/emqx/etc/emqx.conf or override from environment variable EMQX_NODE__COOKIE NOTE: Use the same config…...

Web前端:开始学习ReactJS需要知道什么?
毫无疑问,ReactJS是前端开发者中最著名的库之一,它的受欢迎程度与日俱增。用ReactJS构建的网站看起来非常棒,大多数开发新手都被它吸引住了。然而,许多新人和有经验的开发人员在没有首先了解先决条件的情况下,就直接用…...

卡诺图化简
1.相关概念 最小项:函数的某个乘积项包含了函数的全部变量(原变量或反变量的形式),且每个变量仅出现一次,则这个乘积项为该函数的一个标准积项。 最小项中的原变量记为1,反变量记为0,当变量顺序…...
带你了解软件测试是做什么的
软件测试是互联网技术中一门重要的学科,它是软件生命周期中不可或缺的一个环节,担负着把控、监督软件的质量的重任。 人才稀缺,对于求职者来说就意味着机会。但是很多想学习软件测试的人对这个学科并不了解,也不知道该如何学习&a…...
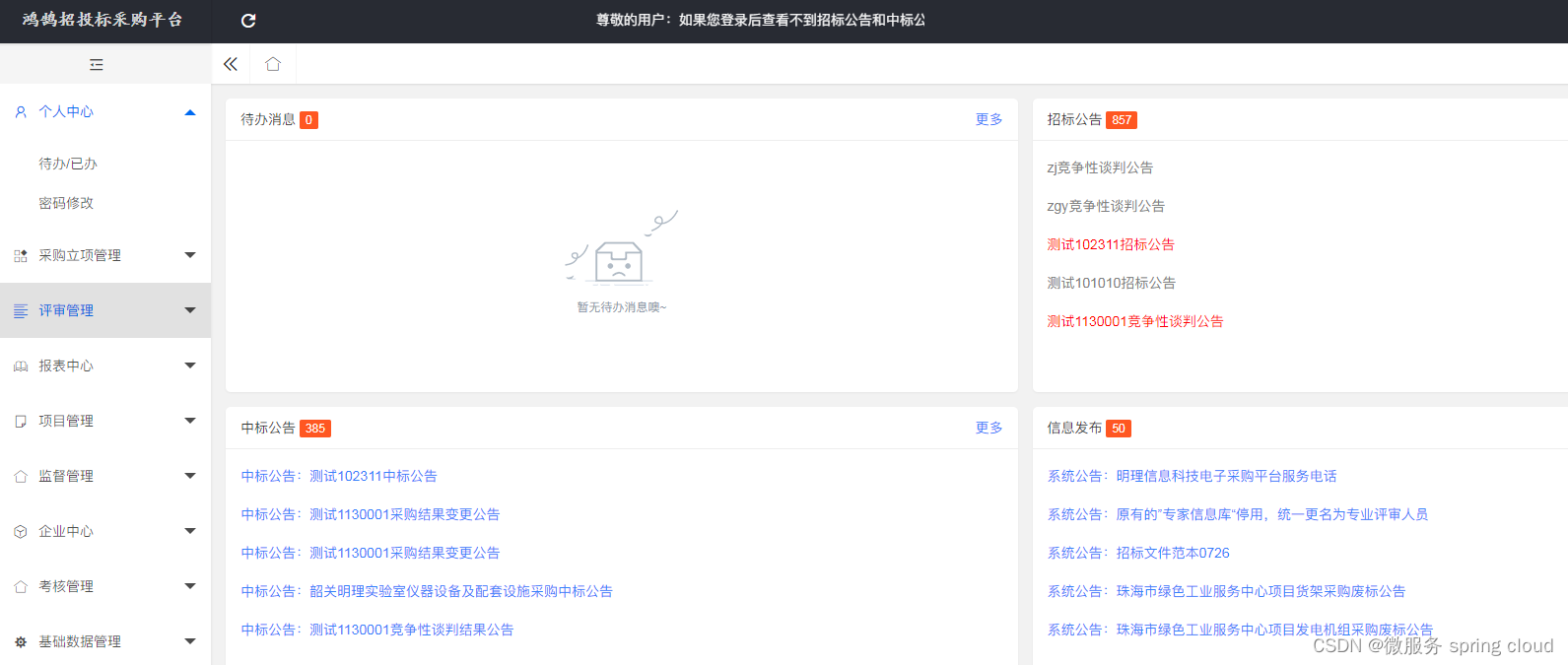
企业电子招投标采购系统源码之功能模块功能描述
功能模块: 待办消息,招标公告,中标公告,信息发布 描述: 全过程数字化采购管理,打造从供应商管理到采购招投标、采购合同、采购执行的全过程数字化管理。通供应商门户具备内外协同的能力,为外…...

职场中的高手,是如何高质量解决问题?
职场总会遇见很多新问题,高手会从容应对,因为他们学习了一套通 用理论,可以处理工作当中的大部分内容,剩下的一部分能够用快速 提问的方式找到思路。 记得几年前有个同事 A,下午四点多项目突然丢过来一个活,…...
报表生成工具Stimulsoft中的电子签名和 PDF 数字签名
Stimulsoft Reports 是一款报告编写器,主要用于在桌面和Web上从头开始创建任何复杂的报告。可以在大多数平台上轻松实现部署,如ASP.NET, WinForms, .NET Core, JavaScript, WPF, Angular, Blazor, PHP, Java等,在你的应用程序中嵌入报告设计器…...
【Hello Linux】Linux环境下写的第一个程序 -- 进度条
作者:小萌新 专栏:Linux 作者简介:大二学生 希望能和大家一起进步! 本篇博客简介:写出Linux中的第一个小程序 进度条 进度条小程序行缓冲区概念\r 和 \n进度条代码和演示行缓冲区概念 我们首先用两段代码来感受下行缓…...

【基础】性能测试,从0到实战(手把手教,非常实用)
一、性能基础 什么是性能测试--->本质? 基于协议来模拟用户发送的请求(业务模拟),对服务器形成一定负载。关注点:时间性能、空间性能与界面无关 性能测试分类 性能测试(狭义) 性能测试方法是通过模…...
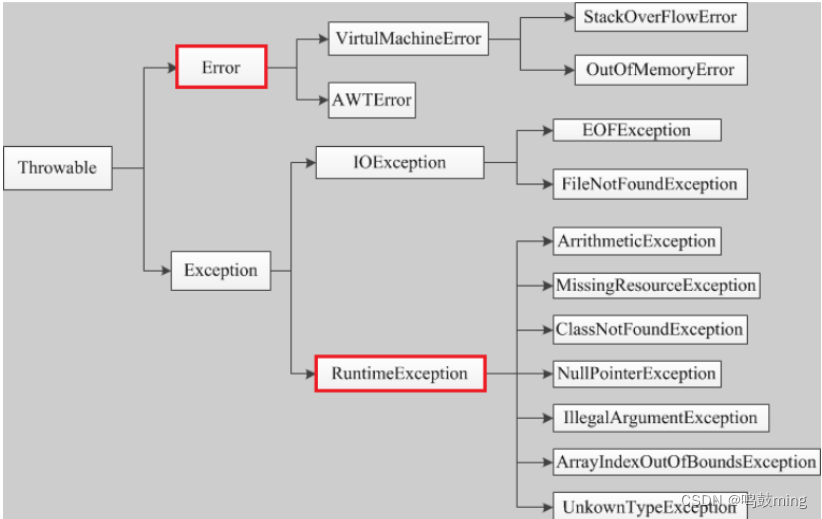
07-Java异常分类以及处理机制
1.异常概念 Java标准库内建了一些通用的异常,这些类以Throwable为顶层父类。Throwable又派生出Error类和Exception类。 1.错误:是程序无法处理的错误,表示运行应用程序中较严重问题。大多数错误与代码编写者执行的操作无关,而表示…...

用到的C++的相关知识-----未完待续
文章目录前言一、vector函数的使用1.1 构造向量二、常用函数2.1 矩阵输出函数2.2 向量输出函数2.3 矩阵的使用2.4三、new的用法3.1 内存的四种分区3.2 new的作用3.33.4四、4.14.24.34.4总结前言 只是为方便学习,不做其他用途 一、vector函数的使用 有关的文章 C v…...

JavaScript刷LeetCode拿offer-贪心算法
前言 学习算法的时候,总会有一些让人生畏的名词,比方动态规划,贪心算法 等,听着就很难;而这一 part 就是为了攻破之前一直没有系统学习的 贪心算法; 有一说一,做了这些贪心题,其实…...

selenium
下载并安装selenium 安装:cmd中执行 pip install -i https://pypi.douban.com/simple selenium执行完成后 pip show selenium 可查看安装是否成功安装浏览器驱动,查看当前浏览器的版本选择合适的驱动并下载 chrome的链接:https://chromedrive…...

SpringMVC的视图
转发视图ThymeleafView若使用的视图技术为Thymeleaf,在SpringMVC的配置文件中配置了Thymeleaf的视图解析器,由此视图解析器解析之后所得到的是ThymeleafView。解析:当控制器方法中所设置的视图名称没有任何前缀时,此时的视图名称会…...
idea使用本地代码远程调试线上运行代码---windows环境
场景: 今天在书上看了一个代码远程调试的方法,自己本地验证了一下感觉十分不错!! windows环境: 启动测试jar包:platform-multiappcenter-base-app-1.0.0-SNAPSHOT.jar 测试工具:postman,idea 应…...
简单记录简单记录
目录1.注册Gmail2.注册ChatGPT3.验证“真人”使用4.开始使用1.注册Gmail 第一步先注册一个谷歌邮箱,你也可以使用微软账号,大部分人选择使用gmail。 申请谷歌邮箱 选择个人用途创建账号即可。 📌温馨提示: 你直接使用guo内的网…...
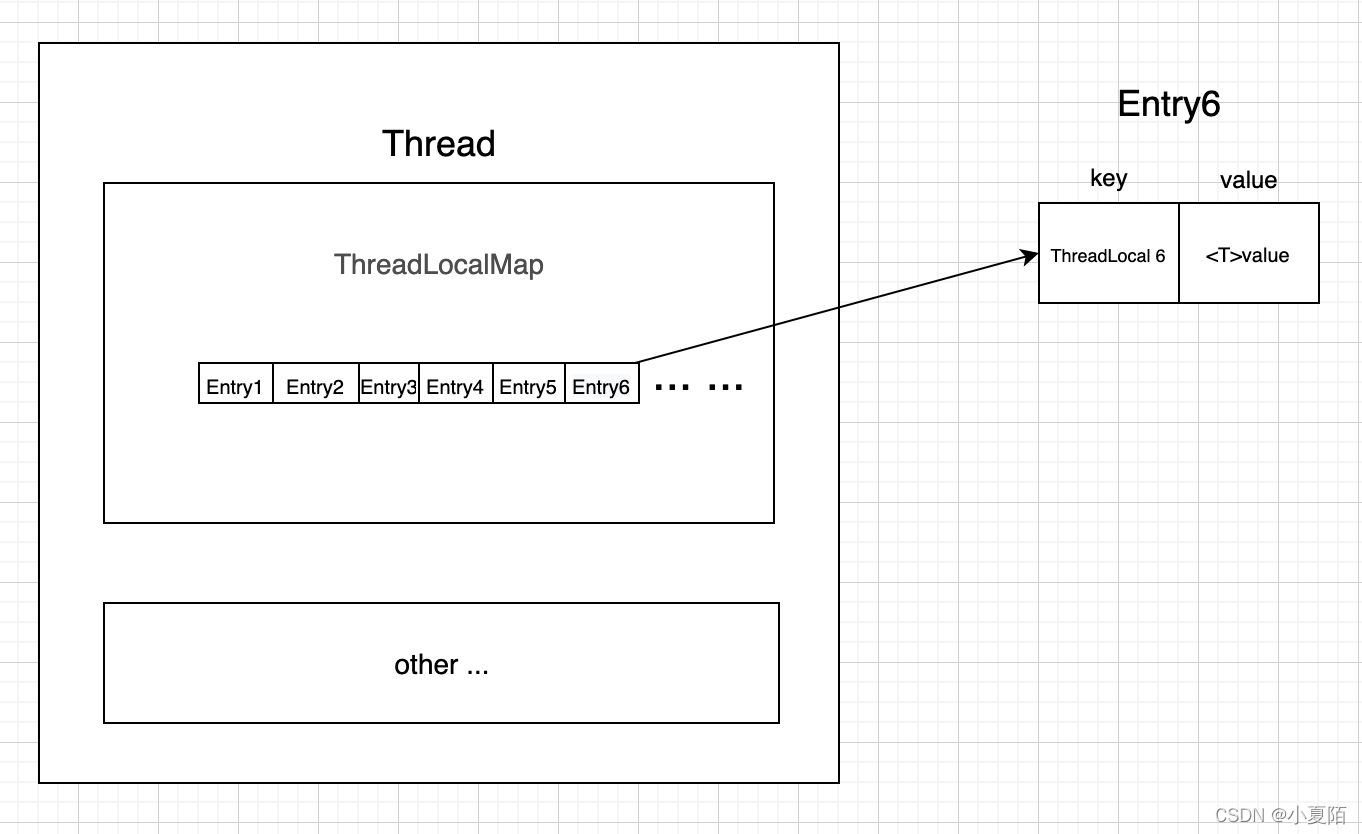
源码系列 之 ThreadLocal
简介 ThreadLocal的作用是做数据隔离,存储的变量只属于当前线程,相当于当前线程的局部变量,多线程环境下,不会被别的线程访问与修改。常用于存储线程私有成员变量、上下文,和用于同一线程,不同层级方法间传…...
——特点及关键字)
C语言入门(1)——特点及关键字
1、C特点及与Java区别 1.1、C特点 面向过程 一般用于嵌入式开发、编写最底层的程序、操作系统 可以直接操作内存 可以封装动态库 不容易跨平台 有指针 可以直接操作串口 线程更加灵活 和硬件打交道速度是最快的 1.2、和Java区别 C是C的增强版,增加了一些新的特性&…...

react中useEffect和useLayoutEffect的区别
布局上 useEffect在浏览器渲染完成后执行useLayoutEffect在DOM更新后执行 特点 useLayoutEffect 总是比 useEffect 先执行;useLayoutEffect与componentDidMount、componentDidUpdate调用时机相同,都是在DOM更新后,页面渲染前调用࿱…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...
