【智能计算数学】微积分
高数
- 问题解决流程
- 引例:回归
- 回归
- 引例:分类
- 分类
- 线性可分
- FLD
- 线性不可分
- 智能计算讨论范围
- 下降法
- 为什么要用下降法?- 解析解很难写出公式或很复杂难计算
- 有哪些常用的下降法?- 梯度下降&高斯-牛顿法
- 梯度下降(Gradient Descent)- 本质:一阶泰勒展开式近似
- 如何找到一阶泰勒展开式的最优解(最小值)?- 柯西一施瓦兹不等式
- 结论:下降最快的方向为梯度的反方向,即梯度下降。
- 牛顿法 - 本质:二阶泰勒展开式近似
- 如何找到二阶泰勒展开式的最优解(最小值)?- 梯度=0
- 分类&回归
- 线性分析
- 常用不等式
- 绝对值不等式
- 柯西不等式
- 算术-几何平均不等式
- 数列极限
- 序列极限
- 上极限
- 下极限
- 级数
- 点集拓扑
- 开集
- 开集性质
- 闭集
- 闭集性质
- 紧集
- Heine-Borel定理
- 例题:判断Rn\mathbb{R^n}Rn和∅\emptyset∅是否开闭紧?
- 函数连续性
- 函数连续定义
- Lipshitz函数是连续函数
- Lipshitz函数与机器学习
- 连续函数逼近
- 拉格朗日插值定理
- 连续函数性质
- 最值定理
- 介值定理
- 不连续函数
- 导数
- 一元函数导数
- 定义
- 意义
- 性质
- 极值定理
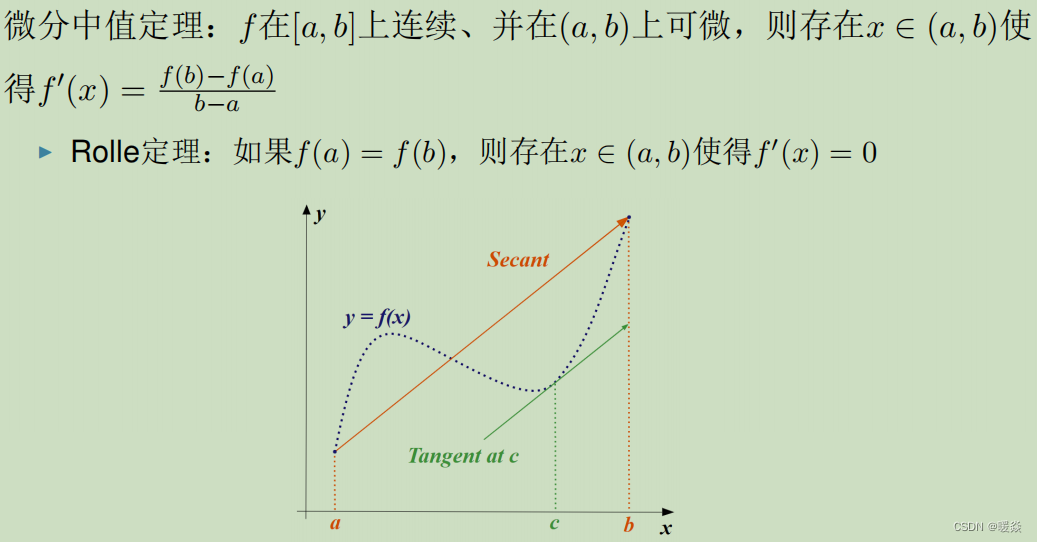
- 微分中值定理
- 洛必达法则
- 常用公式
- C∞C^\inftyC∞
- 多元多值函数
- 可微
- 梯度存在
问题解决流程
idea - math - optimization - algorithm
引例:回归

question:123456x,预测x值为多少?
idea:f(xi)=atxi+b,f(xi)≈yif(x_i)=a^tx_i+b, f(x_i)\approx y_if(xi)=atxi+b,f(xi)≈yi,使用f(x)f(x)f(x)预测新样本xxx。
optimization:使用L1、L2范数度量f(xi)f(x_i)f(xi)和yiy_iyi的差距,即loss function。如何求出参数使得loss function最小?- 偏导数为0。
algorithm:GD、Newton’s method
回归
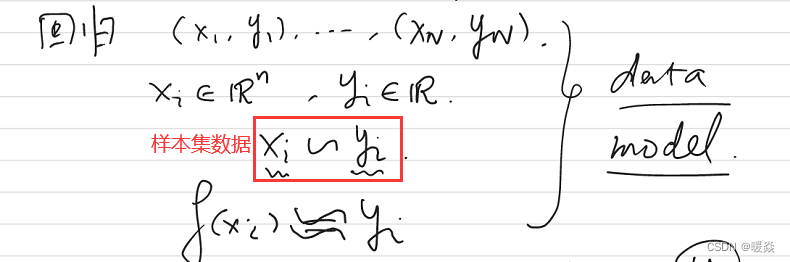



引例:分类
分类
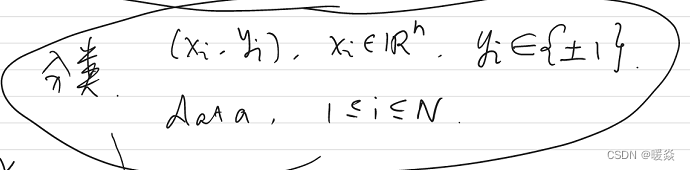
线性可分

FLD

FLD思想:同类点近,不同点远。
根据这个思想,实际的做法是找一条直线,其方向为ω\omegaω,对线性可分的点进行投影,在该直线上,同类点的投影点更近,异类点的投影点更远。进而做一条垂直于该直线的分类线。
先找到投影λ与xi的关系,然后利用w与v垂直内积为0,求出投影λ的表达式,

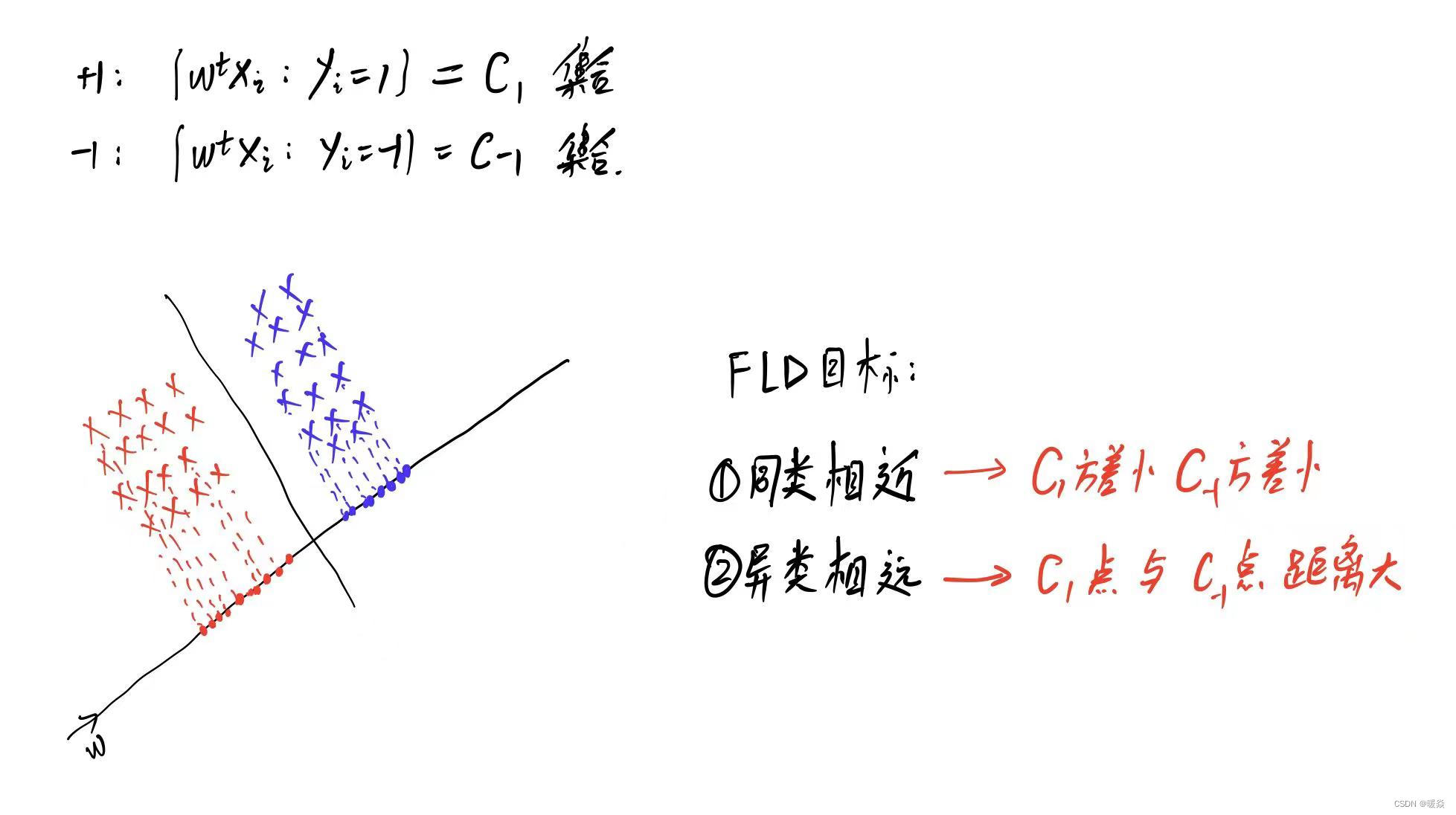

同类相近:要使得C1方差小和C-1的方差小,则将两个优化问题合并为一个优化问题。
异类相远:没有办法计算所有点,所以选择代表性的均值的距离作为两个集合的距离。
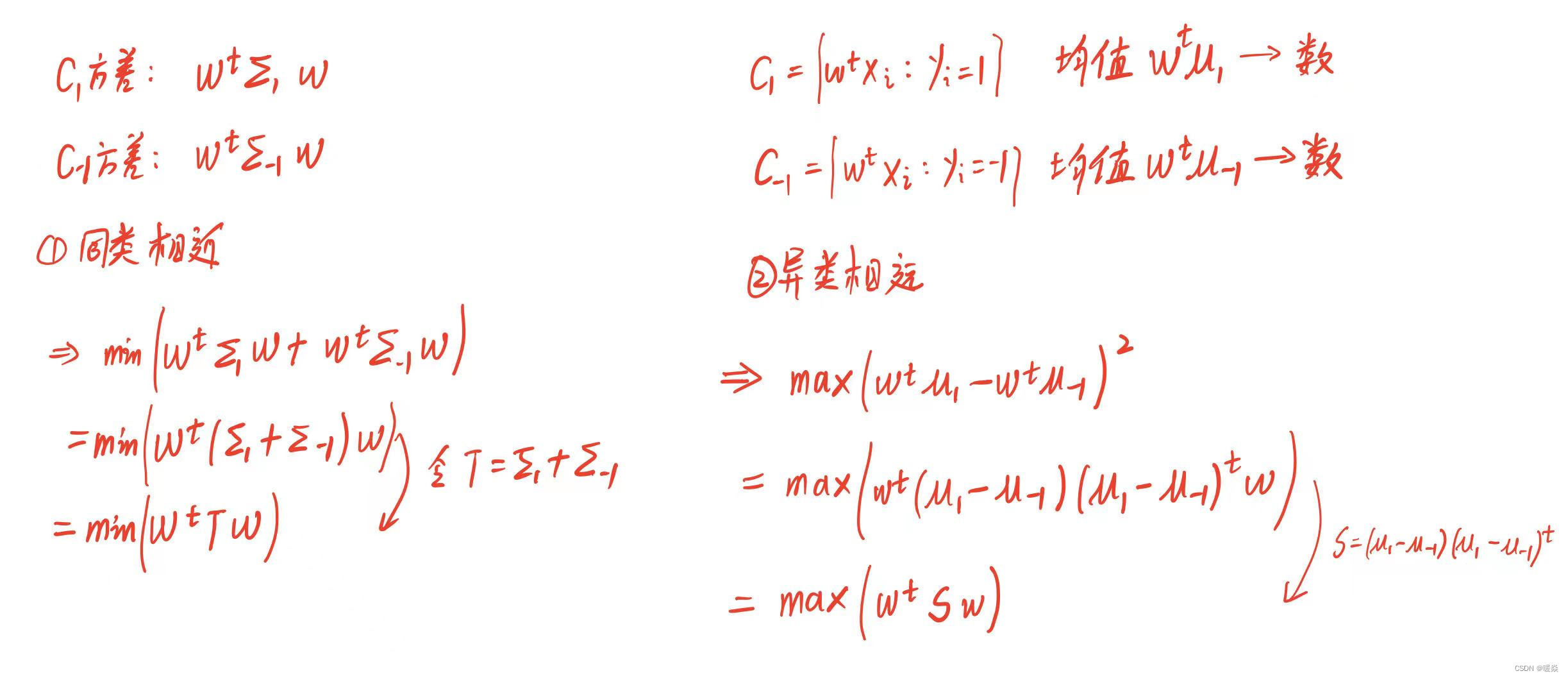
再次将两个优化目标合并为一个单优化目标进行优化。
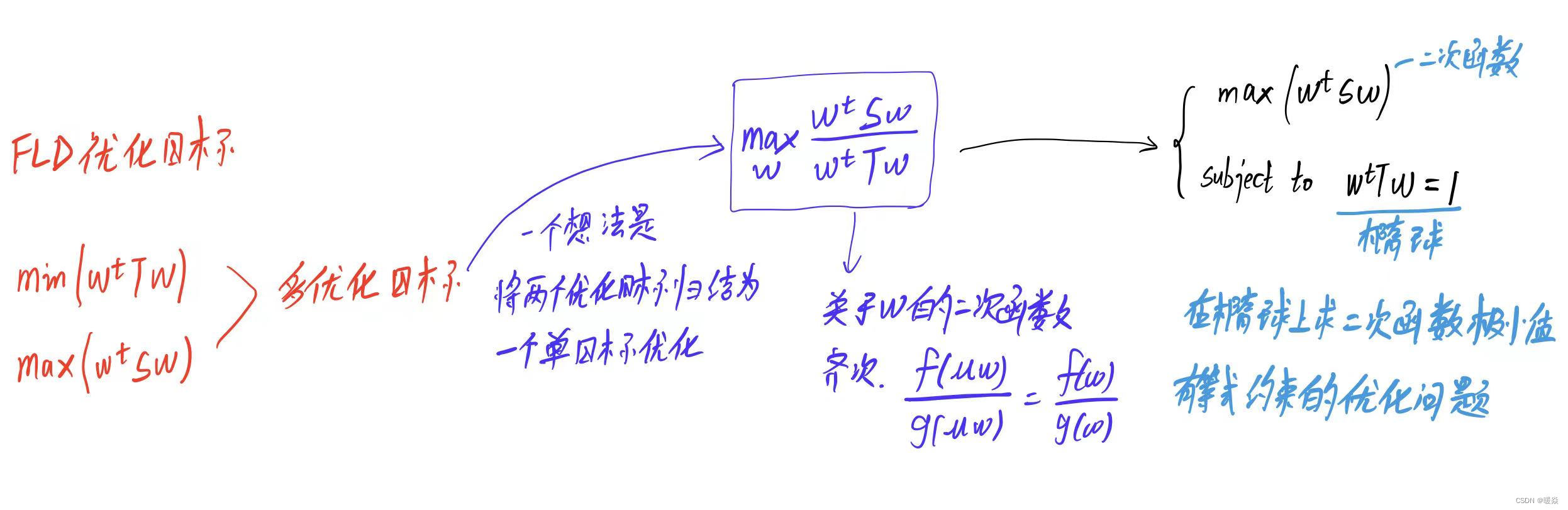
线性不可分
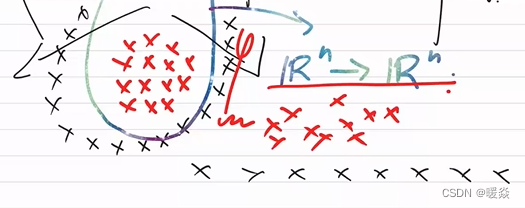
智能计算讨论范围
智能计算讨论的是问题解决流程中的math和optimization。

下降法
为什么要用下降法?- 解析解很难写出公式或很复杂难计算
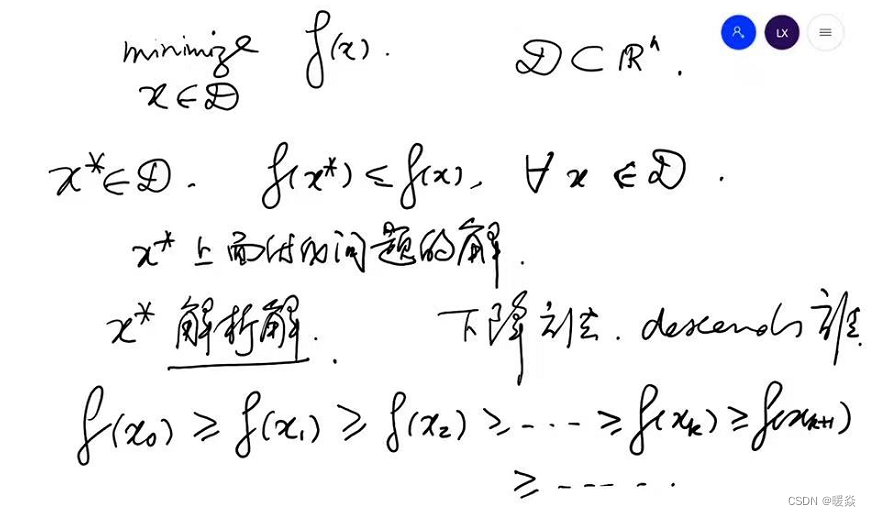
考虑求极值问题场景,需要找到一个x∗x^*x∗使得f(x∗)f(x^*)f(x∗)小于等于邻域内的任意f(x)f(x)f(x),x∗x^*x∗是极小值问题的解,因为x∗x^*x∗的解析解很难写出公式或者可以写出但是公式很复杂难计算,所以考虑使用下降法。
解析解:指通过严格的公式所求得的解。即包含分式、三角函数、指数、对数甚至无限级数等基本函数的解的形式。给出解的具体函数形式,从解的表达式中就可以算出任何对应值。解析解为一封闭形式的函数,因此对任一独立变量,皆可将其代入解析函数求得正确的相依变量。因此,解析解也称为闭式解。
解析法:用来求得解析解的方法称为解析法,解析法是常见的微积分技巧,如分离变量法等。
下降法亦称极小化方法,是一类重要的迭代法。这类方法将方程组求解问题转化为求泛函极小问题。
使用下降法,找出一系列函数值递减的f(x)f(x)f(x)序列,这个下降过程不是一直持续下去的过程,根据一些停止条件得到一个xkx_kxk时,这个xkx_kxk即优化问题的解x∗x^*x∗。
有哪些常用的下降法?- 梯度下降&高斯-牛顿法
梯度下降(Gradient Descent)- 本质:一阶泰勒展开式近似
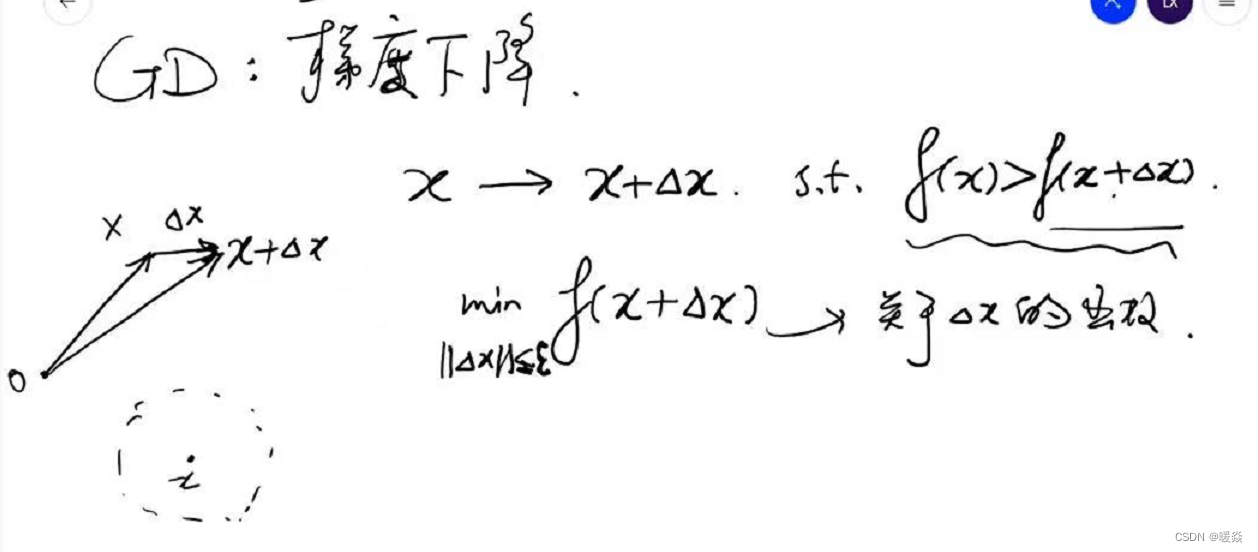
优化问题:在xxx的邻域内,找到一个x+Δxx+ \Delta xx+Δx,使得f(x)>f(x+Δx)f(x)\gt f(x+\Delta x)f(x)>f(x+Δx),且f(x+Δx)f(x+\Delta x)f(x+Δx)在该邻域最小。
数学问题:如何找到该邻域最小f(x+Δx)f(x+\Delta x)f(x+Δx)?
问题难点:因为f(x)f(x)f(x)优化问题的解析解不容易求解,因此f(x+Δx)f(x+\Delta x)f(x+Δx)优化问题的解析解也不容易求解。
解决方法:考虑f(x+Δx)f(x+\Delta x)f(x+Δx)的线性近似——一阶泰勒展开式。将min∣∣Δx∣∣≤εf(x+Δx)\underset {||\Delta x||\le \varepsilon}{min} f(x+\Delta x)∣∣Δx∣∣≤εminf(x+Δx)问题转换为min∣∣Δx∣∣≤ε(f(x)+atΔx)\underset {||\Delta x||\le \varepsilon}{min} (f(x)+a^t \Delta x)∣∣Δx∣∣≤εmin(f(x)+atΔx),因为min∣∣Δx∣∣≤ε(f(x)+atΔx)\underset {||\Delta x||\le \varepsilon}{min} (f(x)+a^t \Delta x)∣∣Δx∣∣≤εmin(f(x)+atΔx)中f(x)f(x)f(x)是固定的,Δx\Delta xΔx是变量,所以问题可再次简化为min∣∣Δx∣∣≤εatΔx\underset {||\Delta x||\le \varepsilon}{min} a^t \Delta x∣∣Δx∣∣≤εminatΔx。
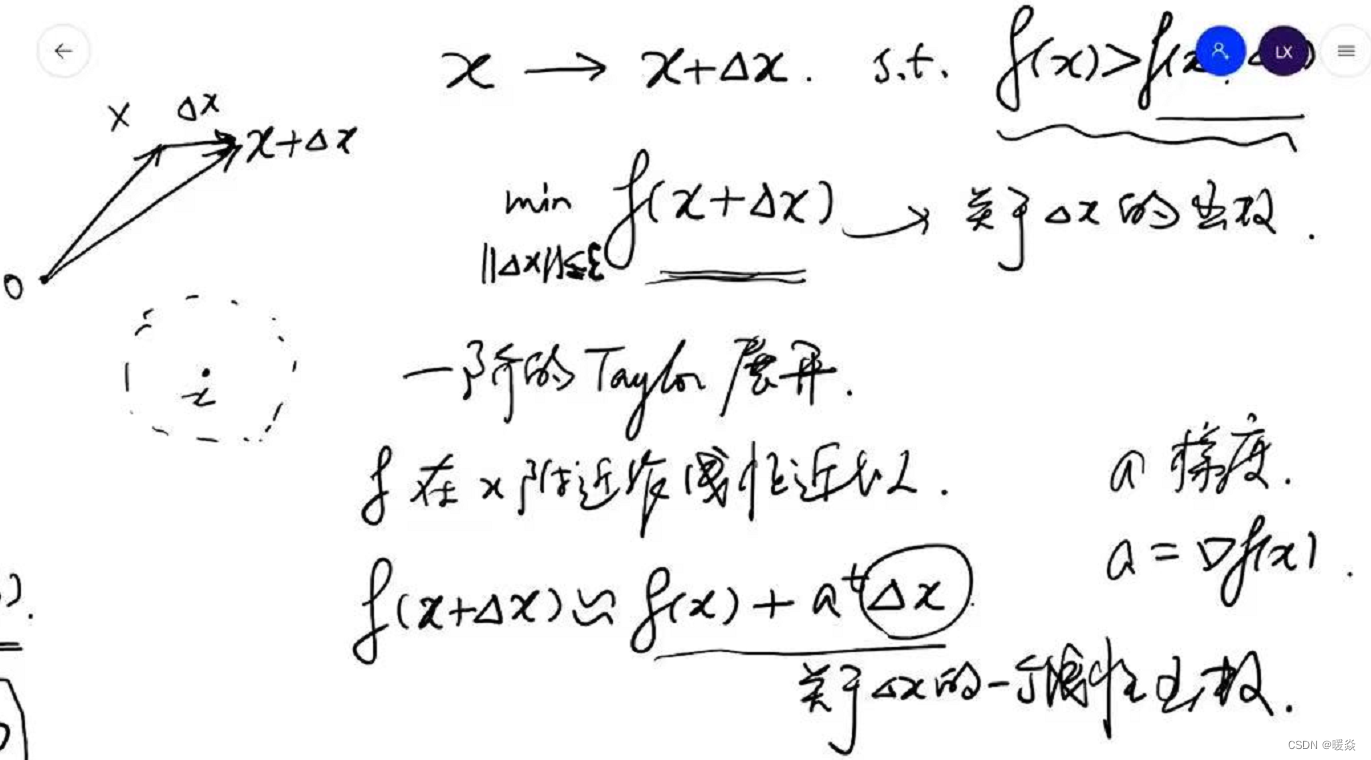
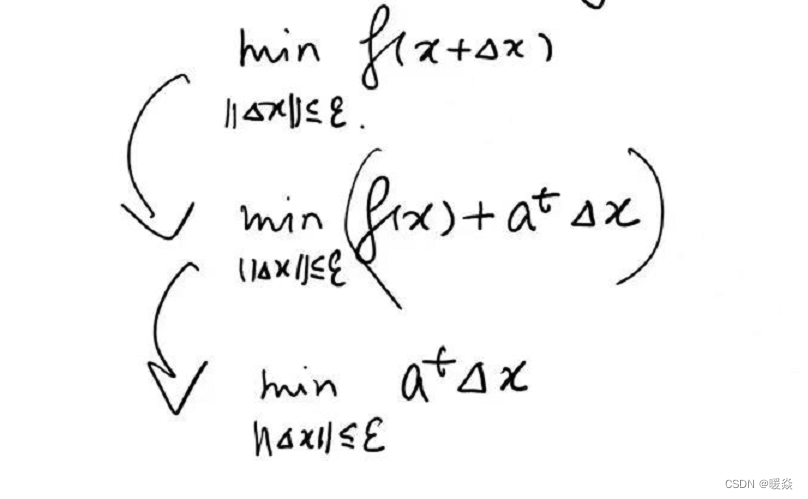
如何找到一阶泰勒展开式的最优解(最小值)?- 柯西一施瓦兹不等式
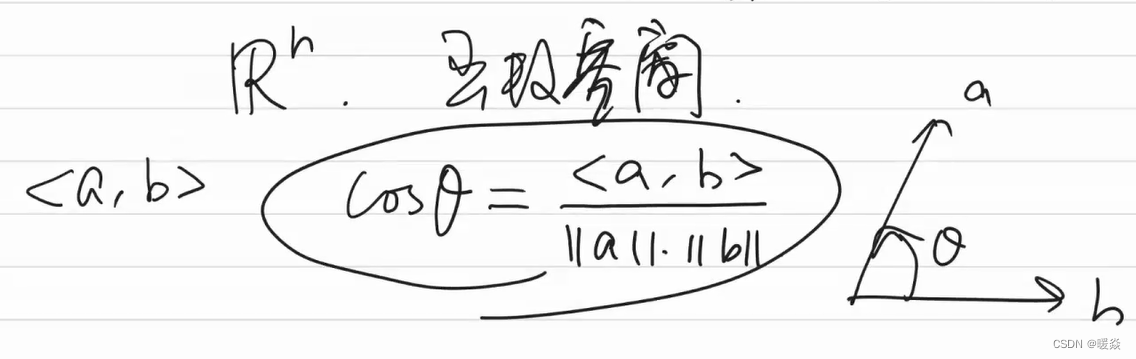
根据柯西一施瓦兹不等式(Cauchy-Schwarz inequality),atΔxa^t \Delta xatΔx 的最小值是显而易见的。
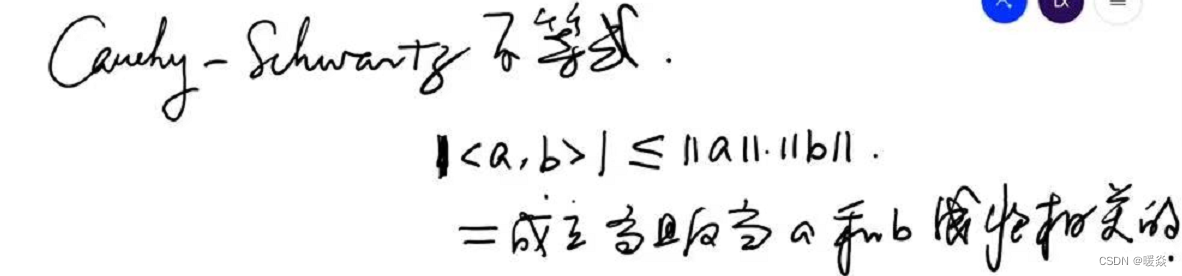
由以上不等式可得:−∣∣a∣∣⋅∣∣b∣∣≤<a,b>≤∣∣a∣∣⋅∣∣b∣∣-||a||·||b|| \le <a,b> \le ||a||·||b||−∣∣a∣∣⋅∣∣b∣∣≤<a,b>≤∣∣a∣∣⋅∣∣b∣∣。
当且仅当a和b共线同向时,a和b线性正相关,<a,b>≤∣∣a∣∣⋅∣∣b∣∣<a,b> \le ||a||·||b||<a,b>≤∣∣a∣∣⋅∣∣b∣∣成立。
当且仅当a和b共线反向时,a和b线性负相关,−∣∣a∣∣⋅∣∣b∣∣≤<a,b>-||a||·||b|| \le <a,b>−∣∣a∣∣⋅∣∣b∣∣≤<a,b>成立。
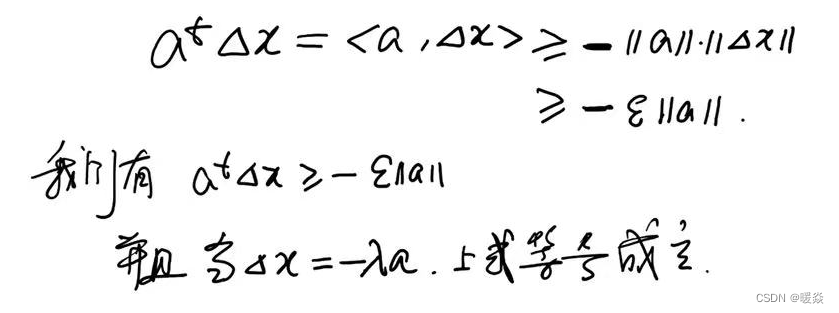
当Δx=−λa\Delta x=-\lambda aΔx=−λa时,表示Δx\Delta xΔx与aaa线性负相关,共线反向,atΔx=−ε∣∣a∣∣a^t \Delta x=-\varepsilon ||a||atΔx=−ε∣∣a∣∣成立。
一阶泰勒展开式中,a表示梯度,所以下降最快的方向为梯度的反方向。
结论:下降最快的方向为梯度的反方向,即梯度下降。
λ\lambdaλ即为学习率。
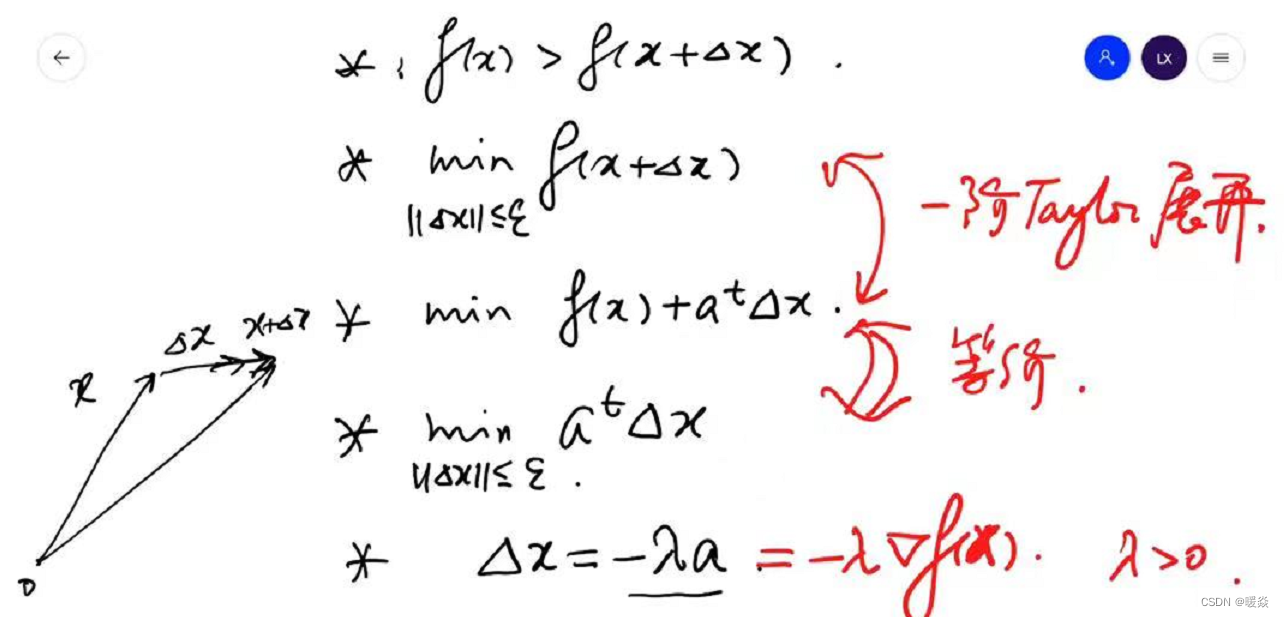
牛顿法 - 本质:二阶泰勒展开式近似
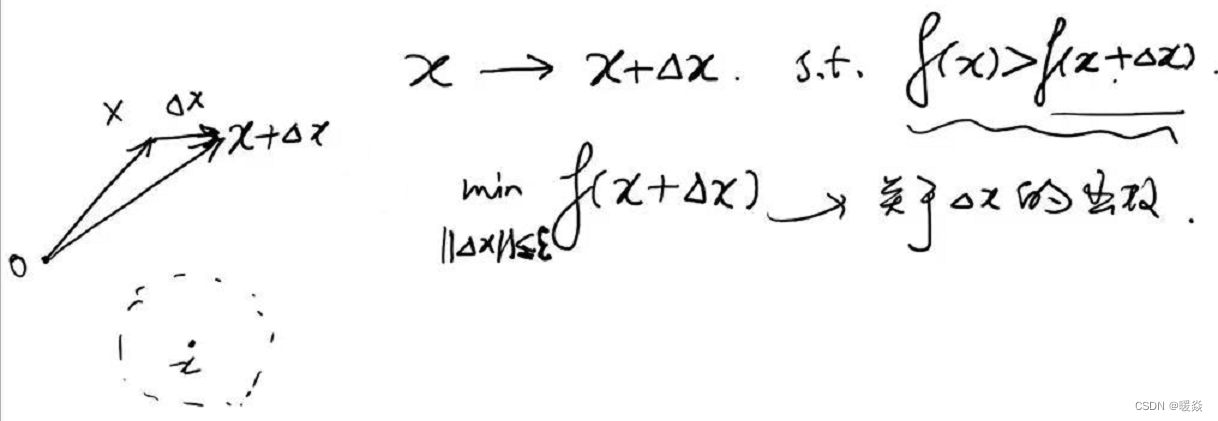
优化问题:在xxx的邻域内,找到一个x+Δxx+ \Delta xx+Δx,使得f(x)>f(x+Δx)f(x)\gt f(x+\Delta x)f(x)>f(x+Δx),且f(x+Δx)f(x+\Delta x)f(x+Δx)在该邻域最小。
数学问题:如何找到该邻域最小f(x+Δx)f(x+\Delta x)f(x+Δx)?
问题难点:因为f(x)f(x)f(x)优化问题的解析解不容易求解,因此f(x+Δx)f(x+\Delta x)f(x+Δx)优化问题的解析解也不容易求解。
解决方法:考虑f(x+Δx)f(x+\Delta x)f(x+Δx)的线性近似——二阶泰勒展开式。将min∣∣Δx∣∣≤εf(x+Δx)\underset {||\Delta x||\le \varepsilon}{min} f(x+\Delta x)∣∣Δx∣∣≤εminf(x+Δx)问题转换为minΔx(f(x)+atΔx+12(Δx)tPΔx)\underset {\Delta x}{min} (f(x)+a^t \Delta x+\frac 1 2 (\Delta x)^t P \Delta x)Δxmin(f(x)+atΔx+21(Δx)tPΔx),其中f(x)f(x)f(x)是固定的,Δx\Delta xΔx是变量,atΔxa^t \Delta xatΔx是关于Δx\Delta xΔx一次函数,12(Δx)tPΔx)\frac 1 2 (\Delta x)^t P \Delta x)21(Δx)tPΔx)是Δx\Delta xΔx二次函数。
因为使用二阶泰勒展开式近似,f(x+Δx)f(x+\Delta x)f(x+Δx)可看做一个二次函数,可以找到全局最优值,而不需要在邻域中讨论,所以可以删除∣∣Δx∣∣≤ε||\Delta x||\le \varepsilon∣∣Δx∣∣≤ε条件。
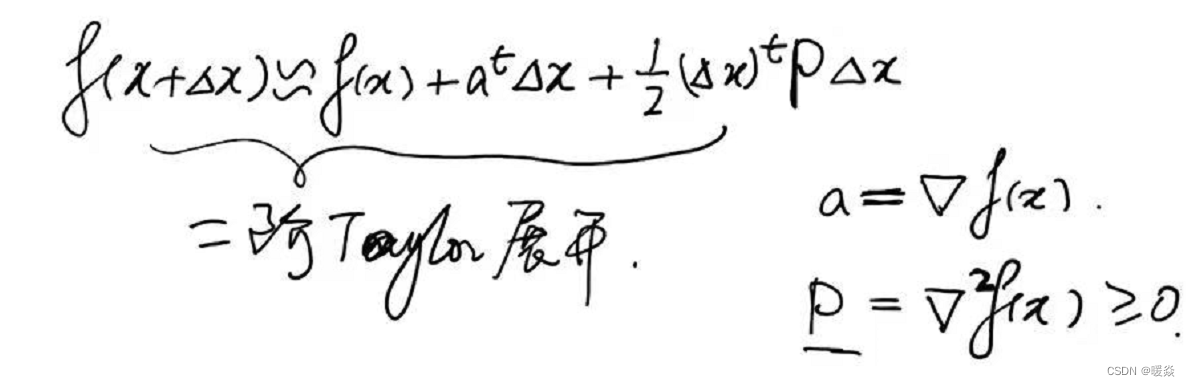
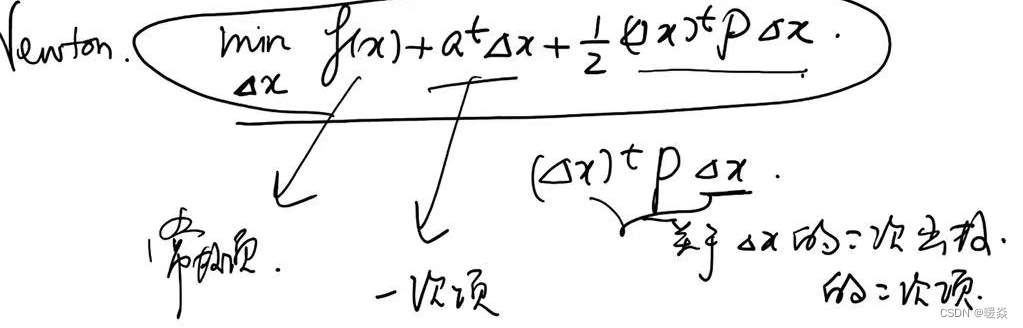
如何找到二阶泰勒展开式的最优解(最小值)?- 梯度=0
令g(Δx)=minΔx(f(x)+atΔx+12(Δx)tPΔx)g(\Delta x)=\underset {\Delta x}{min} (f(x)+a^t \Delta x+\frac 1 2 (\Delta x)^t P \Delta x)g(Δx)=Δxmin(f(x)+atΔx+21(Δx)tPΔx),对g(Δx)g(\Delta x)g(Δx)求关于Δx\Delta xΔx的微分,即梯度∇g\nabla g∇g,令∇g=0\nabla g = 0∇g=0,求出Δx=−P−1a=−(∇2f(x))−1(∇f(x))\Delta x = -P^{-1}a=-(\nabla^2f(x))^{-1}(\nabla f(x))Δx=−P−1a=−(∇2f(x))−1(∇f(x))即为最优解。实际使用时,为了防止(∇2f(x))−1(∇f(x))(\nabla^2f(x))^{-1}(\nabla f(x))(∇2f(x))−1(∇f(x))过大,偏移过远,拟合不准确的问题,需要添加学习率λ\lambdaλ,即Δx=−λ(∇2f(x))−1(∇f(x))\Delta x =-\lambda(\nabla^2f(x))^{-1}(\nabla f(x))Δx=−λ(∇2f(x))−1(∇f(x))。
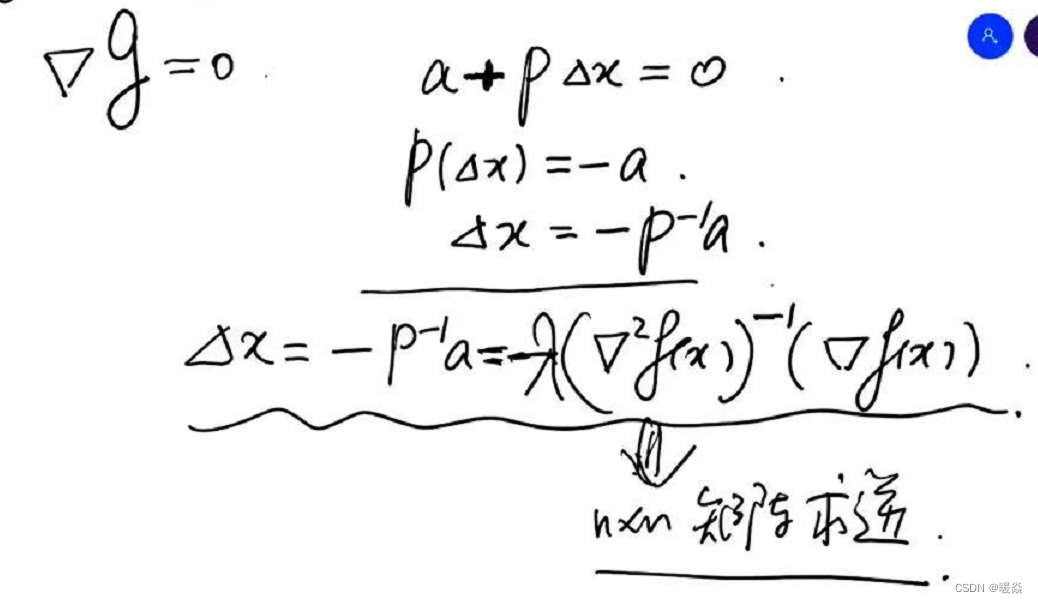
缺点:求解Hessian矩阵的复杂度很高。所以如果Hessian矩阵没有快速计算的方法就会导致迭代过慢,所以牛顿法没有梯度下降法使用频率高。
分类&回归
线性分析
常用不等式
绝对值不等式
∣a1+⋅⋅⋅+an∣≤∣a1∣+⋅⋅⋅+∣an∣|a_1 + · · · + a_n| \le |a_1| + · · · + |a_n|∣a1+⋅⋅⋅+an∣≤∣a1∣+⋅⋅⋅+∣an∣

柯西不等式
<a,b>≤∣∣a∣∣⋅∣∣b∣∣<a,b>\le||a|| \cdot ||b||<a,b>≤∣∣a∣∣⋅∣∣b∣∣
(∑i=1naibi)2≤(∑i=1nai2)(∑i=1nbi2)(\sum_{i=1}^n a_i b_i)^2 \le (\sum_{i=1}^n a_i^2)(\sum_{i=1}^n b_i^2)(∑i=1naibi)2≤(∑i=1nai2)(∑i=1nbi2)
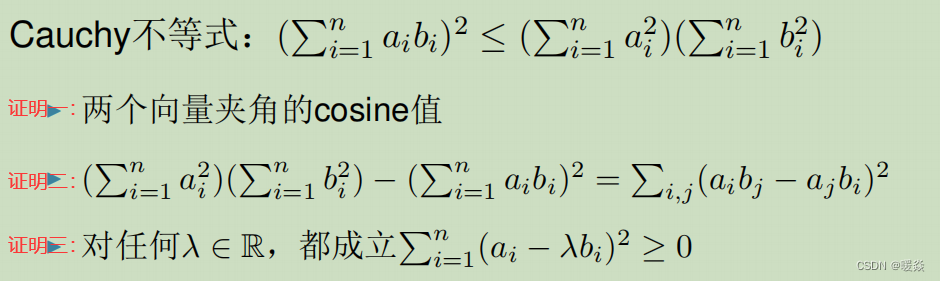

数学研究问题,从群(加)到线性空间(加乘),到赋范线性空间(距离)再到hilbert空间(几何(角度))。
内积的概念很重要,因为有了内积就有了几何结构。
算术-几何平均不等式


数列极限
序列极限
上极限
下极限

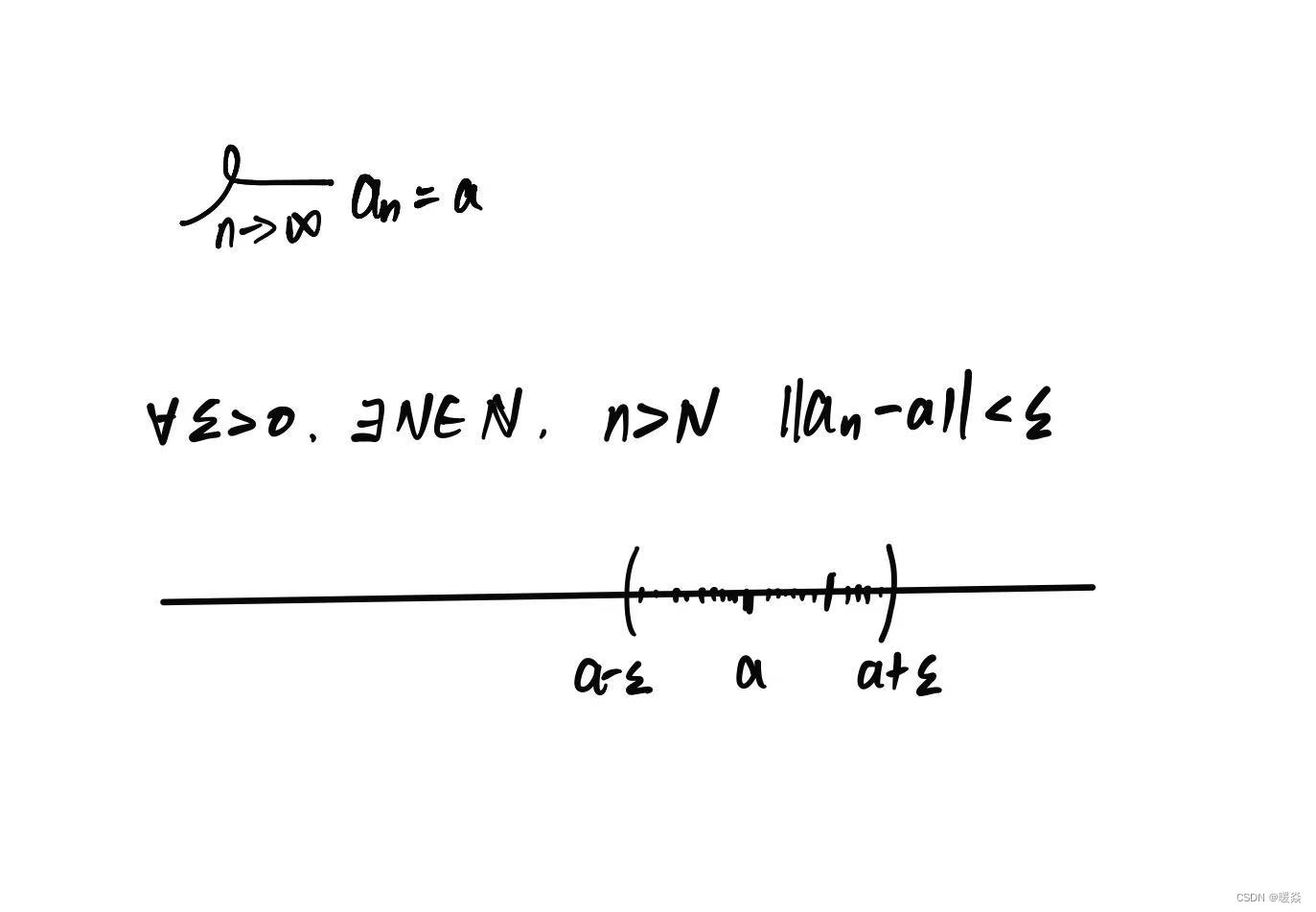
级数
无穷数列和。
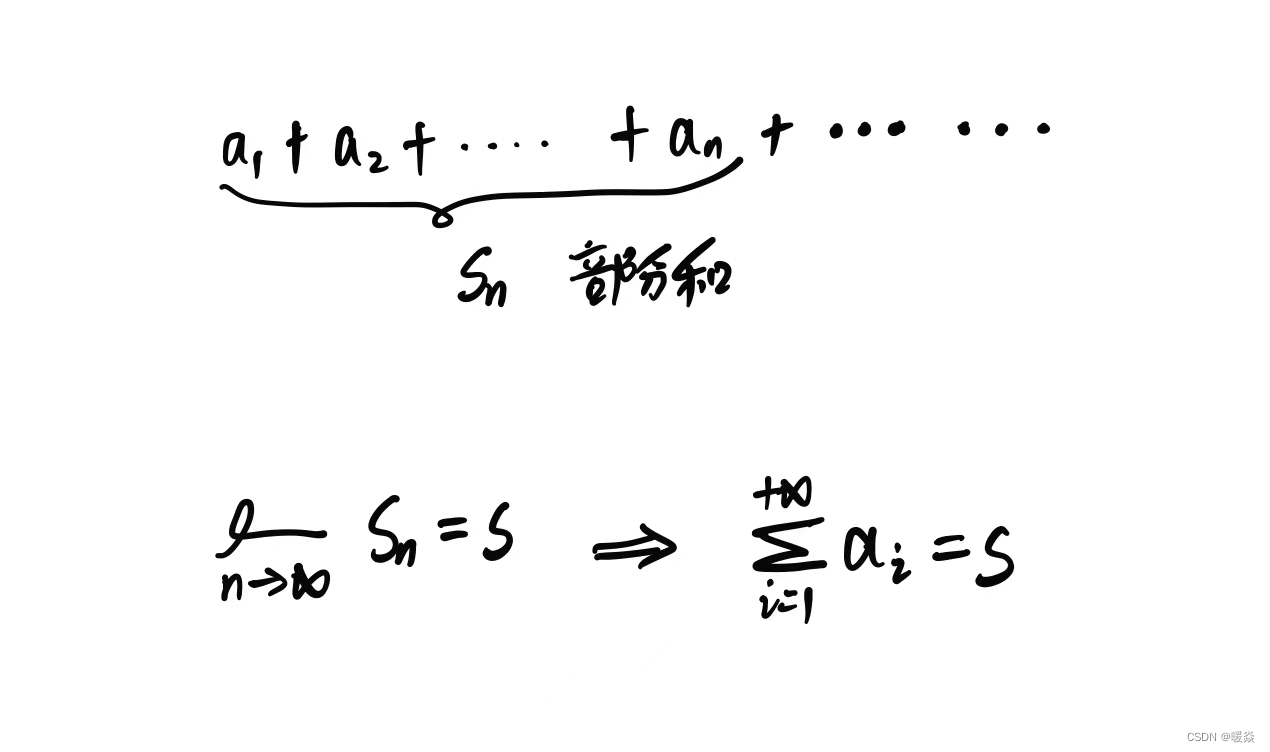

点集拓扑

开集
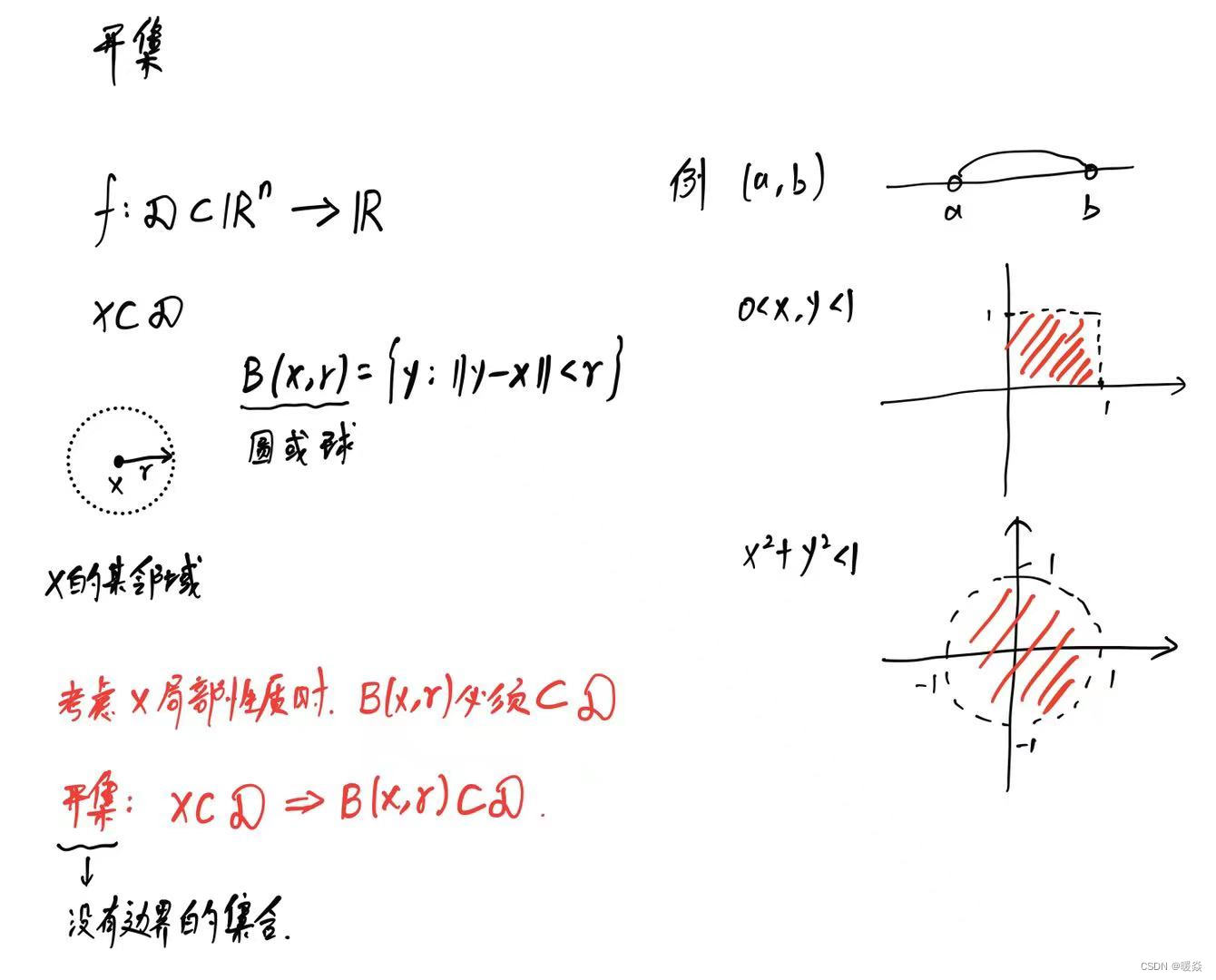
开集性质
任意个开集之并是开集,有限个开集之交是开集。
闭集
“闭”:包含极限点。

闭集性质
任意个闭集之交是闭集,有限个闭集之并是闭集。
紧集
有界闭集。
Heine-Borel定理
Rn\mathbb{R^n}Rn 上紧集的任何开覆盖都存在有限子覆盖。
例题:判断Rn\mathbb{R^n}Rn和∅\emptyset∅是否开闭紧?

Rn\mathbb{R^n}Rn 不是紧集,因为没有边界。
函数连续性
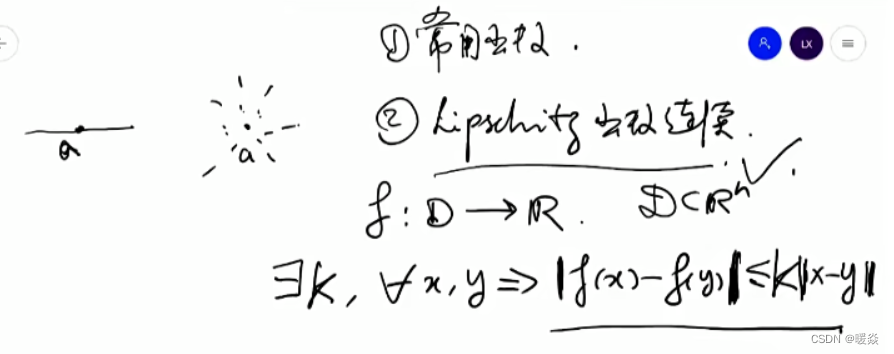
函数连续定义

Lipshitz函数是连续函数

Lipshitz函数与机器学习
参考:Lipschitz函数与机器学习 - gwave的文章 - 知乎
深度学习对输入很敏感,微小的扰动就可能对结果产生很大的影响,将少量精心选择的长臂猿梯度噪声混人熊猫的照片,算法就把熊猫误认为是长臂猿了,Lipschitz常数是种衡量网络稳定性的测度,bound住了输出变化对输入微扰的上限。



连续函数逼近

拉格朗日插值定理


连续函数性质
最值定理

波尔查诺-维尔斯特拉斯定理,又称为致密性定理。指有界数列必有收敛子列。从极限点的角度来叙述致密性定理,就是:有界数列必有极限点。
介值定理
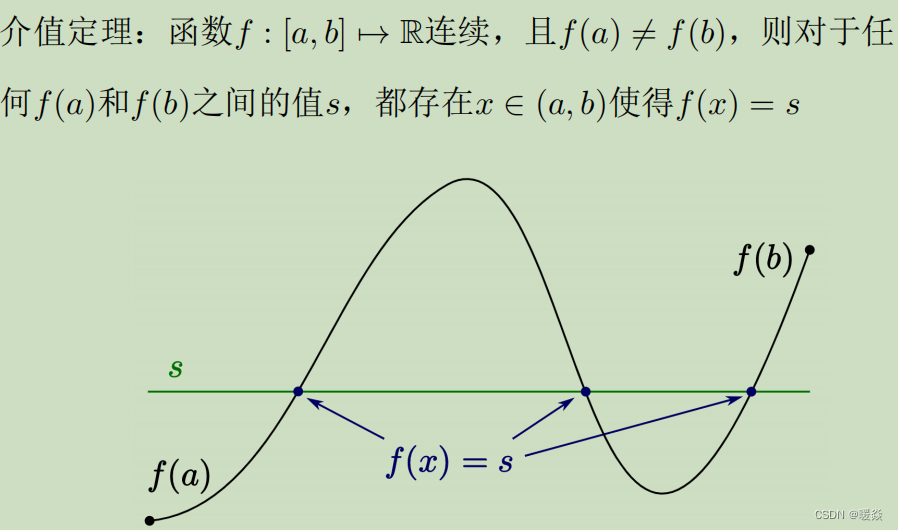
不连续函数

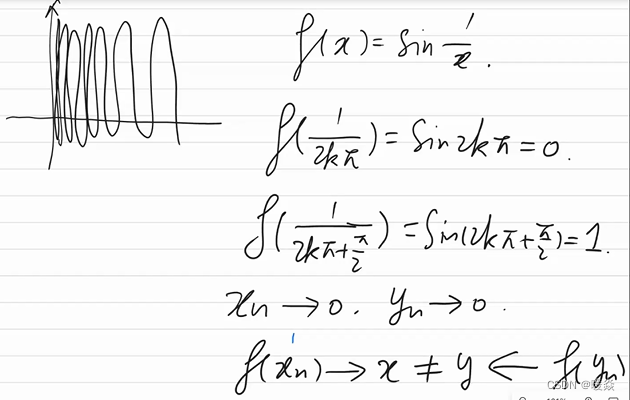
导数
一元函数导数
定义
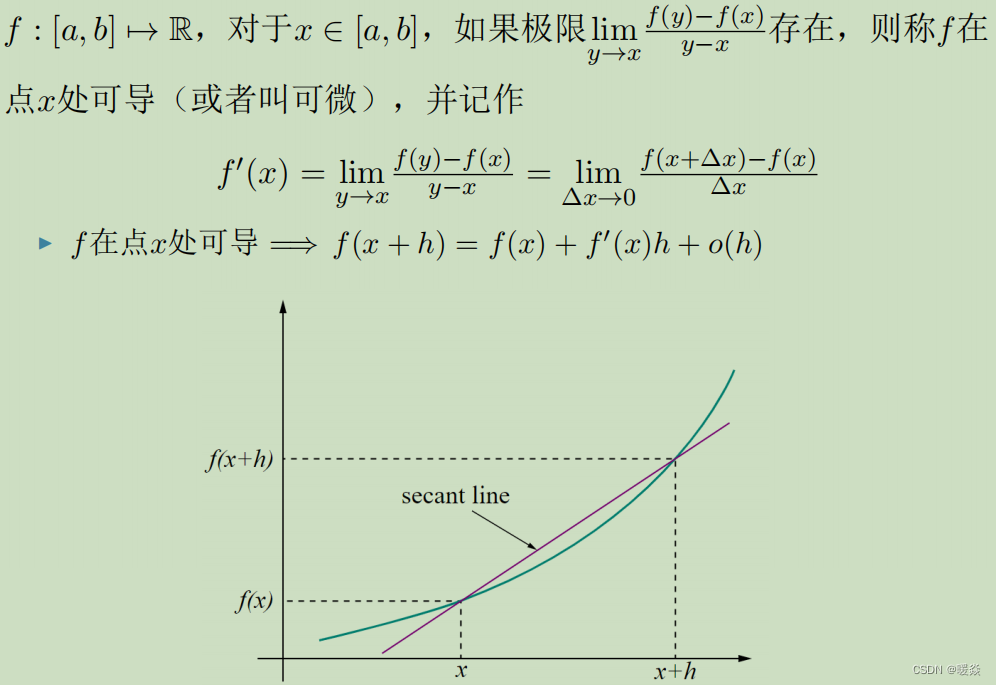
意义

性质
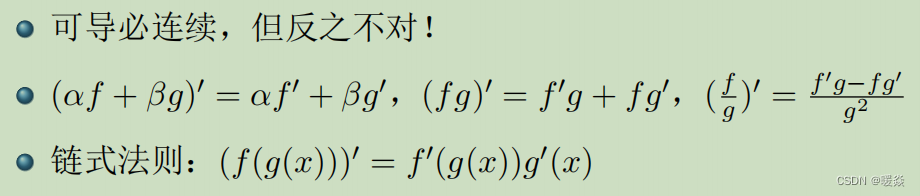
极值定理
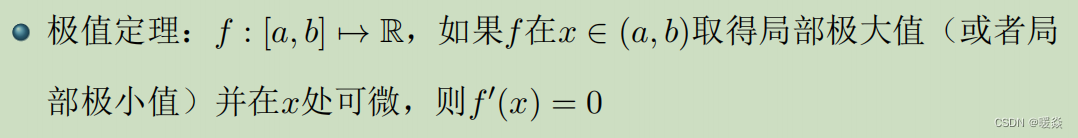
微分中值定理
洛必达法则

常用公式

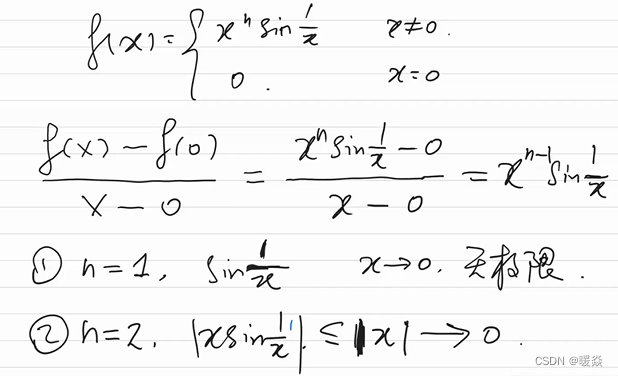
C∞C^\inftyC∞
C1C^1C1:函数一阶导数存在。
C2C^2C2:函数二阶导数存在。
C3C^3C3:函数三阶导数存在。
…
C∞C^\inftyC∞:函数任意阶导数都存在。
多元多值函数
可微
梯度存在
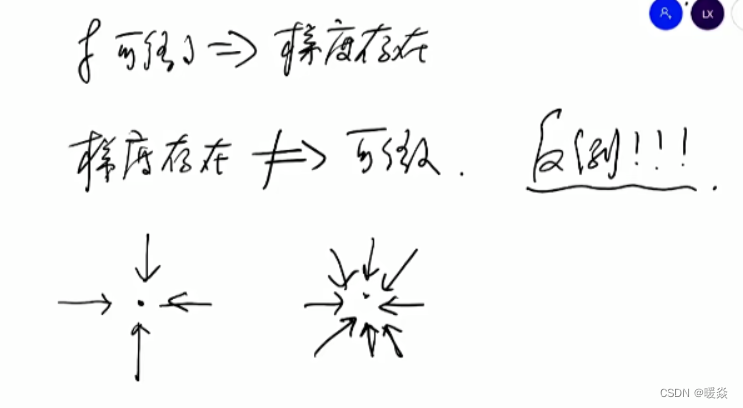
什么情况下梯度存在可以推出函数可微?
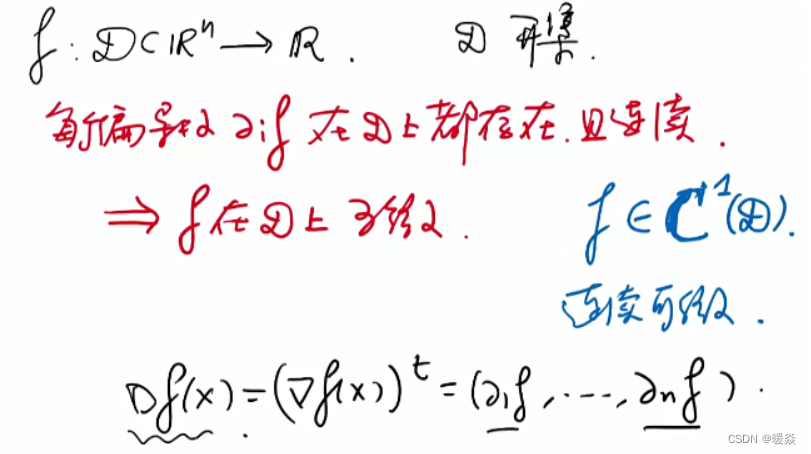

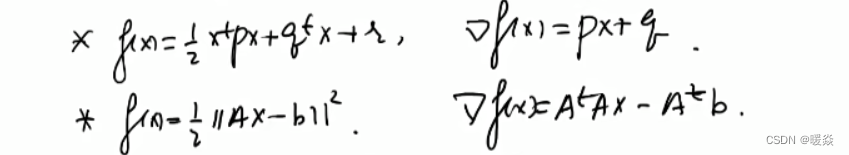


相关文章:

【智能计算数学】微积分
高数问题解决流程引例:回归回归引例:分类分类线性可分FLD线性不可分智能计算讨论范围下降法为什么要用下降法?- 解析解很难写出公式或很复杂难计算有哪些常用的下降法?- 梯度下降&高斯-牛顿法梯度下降(Gradient De…...

win10+RTX4070ti+libtorch部署
环境cuda 11.7、cudnn8.6.0、libtorch1.13.1cu117 注意: 1)libtorch官网进不去的可直接下载 Release version https://download.pytorch.org/libtorch/cu117/libtorch-win-shared-with-deps-1.13.1%2Bcu117.zip Debug version https://download.pytorch.…...

【Python百日进阶-Web开发-Vue3】Day518 - Vue+ts后台项目5:用户列表
文章目录 一、获取用户列表的数据1.1 定义用户列表和角色列表的接口src/request/api.ts1.2 获取用户列表数据src/views/UserView.vue二、定义用户列表数据类型2.1 src/type/user.ts三、展示用户列表内容3.1 element-plus中的Select 选择器3.2 element-plus中的表格插槽3.3 展示…...

Linux内核转储---kdump原理梳理
文章目录Kexec和Kdump设计的区别kexeckdumpKdump的执行流程kexec的实现用户空间kexec内核空间vmcoreKdump的实现可以分为两部分:内核和用户工具。内核提供机制,用户工具在这些机制上实现各种转储策略,内核机制对用户工具的接口是一个系统调用…...
【C++】从0到1入门C++编程学习笔记 - 实战篇:演讲比赛流程管理系统
文章目录一、演讲比赛程序需求1.1 比赛规则1.2 程序功能1.3 程序效果图:二、项目创建2.1 创建项目2.2 添加文件三、创建管理类3.1创建文件3.2 头文件实现3.3 源文件实现四、菜单功能4.1 添加成员函数4.2 菜单功能实现4.3 测试菜单功能五、退出功能5.1 提供功能接口5…...

04 OpenCV位平面分解
1 基本概念 位平面分解的核心思想是将图像的每一个像素分解为多个二进制位,分别存储在不同的位平面上。例如,如果一个图像是8位深度的,则可以分解为8个位平面,每个位平面上存储一个二进制位。 位平面分解在图像压缩中有着重要的…...
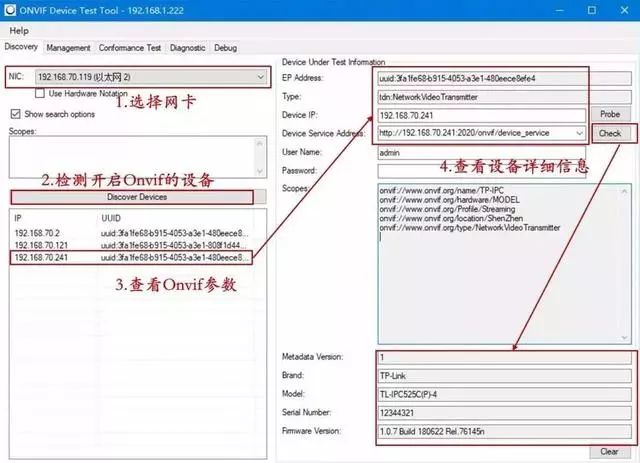
Onvif协议如何判断摄像机支持 —— 筑梦之路
有人就问什么是Onvif协议呢? 全称为:Open Network Video Interface Forum.缩写成Onvif。 翻译过来是:开放型网络视频接口论坛,目的是确保不同安防厂商的视频产品能够具有互通性,这样对整体安防行业才是良性发展。 现…...

情人节new一个对象给你
今天情人节,有没对象的吗?假设你不知道new怎么用,每个人都有两种身份,一种没对象的人,这个时候new一个对象给你,一种是有对象的人,这个delete对象。等你学完这个new和delete知识点,无…...
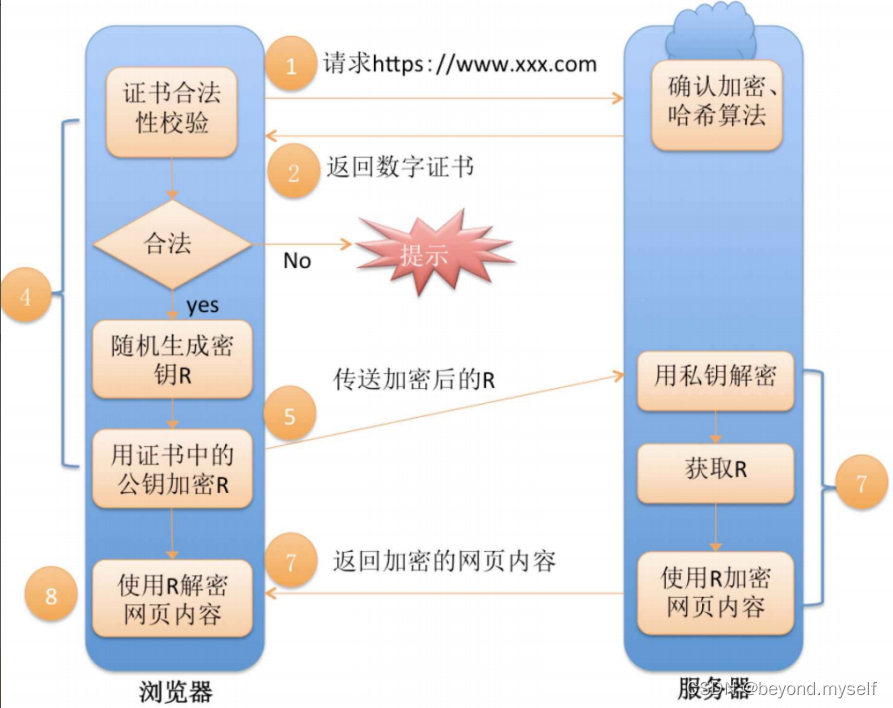
linux篇【15】:应用层-网络https协议
目录 一.HTTPS介绍 1.HTTPS 定义 2.HTTP与HTTPS (1)端口不同,是两套服务 (2)HTTP效率更高,HTTPS更安全 3.加密,解密,密钥 概念 4.为什么要加密? 5.常见的加密方式…...

索引-性能分析-explain
explain 执行计划 explain 执行计划各字段含义 1)id 就是代表 sql 的执行顺序或者表的执行顺序;id相同从上往下执行,id不同,id值越大越先执行;(注:有子查询时就会出现sql执行顺序)…...

mbedtls加密组件使用示例
1 mbedtls aes组件的使用 1.1 AES ECB加解密接口使用 int main(int argc, char *argv[]) {char key[256];char *inbuf calloc(1, 257);char *outbuf calloc(1, 257);char *buf calloc(1,257);char *tmp_outbuf outbuf;char *tmp_buf buf;mbedtls_aes_context aes_ctx;mb…...

如何量测太阳光模拟器的光谱致合度?
太阳模拟器是根据国际法规JIS、IEC60904、美国材料试验协会开发设计的AAA级太阳模拟器。对于100毫米100毫米和200毫米200毫米的光斑尺寸,光斑强度的输出功率范围可以从0.1到1太阳光强度。此外,还提供了灵活的出光方向,以满足用户的研究需求&a…...

网络安全领域中CISP证书八大类都有什么
CISP注册信息安全专业人员 注册信息安全专业人员(Certified Information Security Professional),是经中国信息安全产品测评认证中心实施的国家认证,对信息安全人员执业资质的认可。该证书是面向信息安全企业、信息安全咨询服务…...
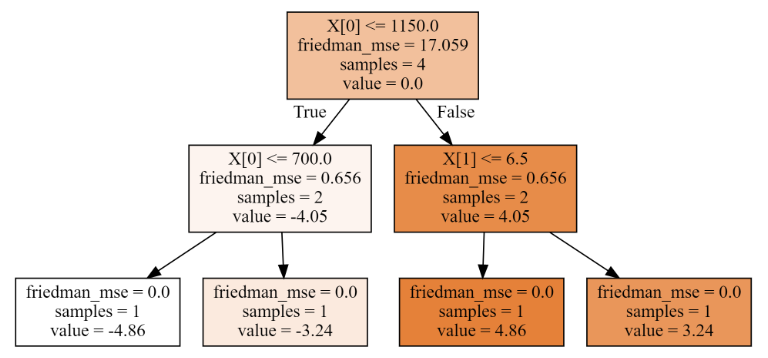
17- 梯度提升回归树GBRT (集成算法) (算法)
梯度提升回归树: 梯度提升回归树是区别于随机森林的另一种集成方法,它的特点在于纠正与加强,通过合并多个决策树来构建一个更为强大的模型。该模型即可以用于分类问题,也可以用于回归问题中。在该模型中,有三个重要参数分别为 n_…...

05 OpenCV色彩空间处理
色彩空间(Color Space)是一种用于描述颜色的数学模型,它将颜色表示为多维向量或坐标,通常由三个或四个独立的分量来表示。不同的色彩空间在颜色的表示方式、可表达颜色的范围、计算速度和应用场景等方面存在差异,不同的…...
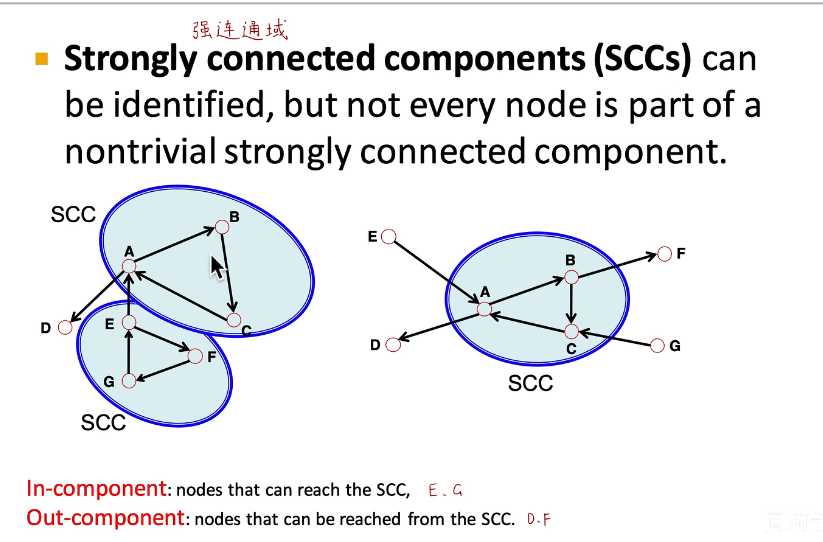
【CS224图机器学习】task1 图机器学习导论
前言:本期学习是由datawhale(公众号)组织,由子豪兄讲解的202302期CS224图机器学习的学习笔记。本次学习主要针对图机器学习导论做学习总结。1.什么是图机器学习?通过图这种数据结构,对跨模态数据进行整理。…...
Powershell Install SQL Server 2022
前言 SQL Server 2022 (16.x) 在早期版本的基础上构建,旨在将 SQL Server 发展成一个平台,以提供开发语言、数据类型、本地或云环境以及操作系统选项。 SQL Server Management Studio (SSMS) 是一种集成环境,用于管理从 SQL Server 到 Azure SQL 数据库的任何 SQL 基础结构…...

Jetson NX2 装机过程
1.固态硬盘安装完成后,系统配置 df -h 查看硬盘使用情况 2.查看Jetson NX的IP地址,以下两个都行 ifconfig ip address show 3.Jetson NX2安装arm64的annaconda3,安装有问题报错illegal instruction,未解决。 4.VNC远程登录 …...

初始C++(四):内联函数
文章目录一.内联函数概念二.内联函数用法三.内联函数的特性四.内联函数和宏一.内联函数概念 以inline修饰的函数叫做内联函数,编译时C编译器会在调用内联函数的地方展开,没有函数调用建立栈帧的开销,内联函数提升程序运行的效率。 二.内联函…...

九、初识卷积
文章目录1、通过边缘检测认识卷积2、Padding3、Strid Convelution4、RGB图像的卷积THE END1、通过边缘检测认识卷积 \qquad在使用神经网络进行图像识别时,神经网络的前几层需要完成对图像的边缘检测任务,所谓的边缘检测就是让计算机识别出一张图片的垂直…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...