传统机器学习(六)集成算法(2)—Adaboost算法原理
传统机器学习(六)集成算法(2)—Adaboost算法原理
1 算法概述
Adaboost(Adaptive Boosting)是一种自适应增强算法,它集成多个弱决策器进行决策。
Adaboost解决二分类问题,且二分类的标签为{-1,1}。注:一定是{-1,1},不能是{0,1}
它的训练过程是通过不断添加新的弱决策器,使损失函数继续下降,直到添加决策器已无效,最终将所有决策器集成一个整体进行决策。
1.1 Adaboost概述
1.1.1 Adaboost的具体操作
- Adaboost会先训练一个弱决策器进行预测,在单个决策器的预测基础上,添加第二个,让预测更准确,在两个决策器的集成决策基础上,添加第三个,让预测更准确,…,如此类推,通过不断添加新的决策器,使损失函数持续下降,直到新增的决策器无法再让损失函数下降,则停止训练。最终将所有决策器集成一个整体进行决策。
- 理论上Adaboost适用于多种决策器,但实际中基本都是以决策树作为决策器,这样的Adboost也称为提升树。在不特指的情况下,
Adboost一般就是指以决策树为决策器的Adaboost算法。 - 个体学习器之间存在强依赖关系、必须串行生成的序列化方法。
- 【提高】那些在前一轮被弱分类器【分错】的样本的权值
- 【减小】那些在前一轮被弱分类器【分对】的样本的权值
- 【加法模型】将弱分类器进行【线性组合】
1.1.2 Adaboost的模型表达式
F ( x ) = a 1 D 1 ( x ) + a 2 D 2 ( x ) + . . . + a m D m ( x ) 其中, D i ( x ) : 第 i 个决策器 a i :决策器的权重系数,为正数 可以看到 , A d a b o o s t 模型就是一系列决策器的加权和。 F(x) = a_1D_1(x) + a_2D_2(x)+...+a_mD_m(x) \\ 其中,D_i(x):第i个决策器\\ a_i:决策器的权重系数,为正数\\ 可以看到,Adaboost模型就是一系列决策器的加权和。 F(x)=a1D1(x)+a2D2(x)+...+amDm(x)其中,Di(x):第i个决策器ai:决策器的权重系数,为正数可以看到,Adaboost模型就是一系列决策器的加权和。
模型的输出是一个数值(即所有决策器的权重和)
-
如果模型的输出是负数,判为-1标签,
-
如果模型的输出是正数,判为 1标签。
一个Adboost模型由以下参数决定:
- 各个决策器自身的模型参数
- 各个决策器的权重
注意:
在每一轮,分别记录好那些被【当前分类器】正确分类和错误分类的样本,在下一轮训练中,提高【错误分类样本】的权值,同时降低【正确分类样本】的权值,用来训练新的弱分类器。这样一来,没有得到正确分类的数据,由于其权值加大,会受到后一轮弱分类器的更大关注。
【加权多数表决】是指:
1、加大【分类误差率】小的弱分类器的权值,使其在表决中起到较大的作用。
2、减小【分类误差率】大的多分类器的权值,使其在表决中起到较小的作用。
1.1.3 前向分布算法
模型求解采用前向分步算法,即逐个逐个决策器训练,先训练第一个,在第一个基础上,训练第二个…每个决策器的训练目标都力求在当前最优(把损失函数降到最低)。直到新增决策器已无法减少误差(或达到最大决策器个数m)。

Adboost的关键点在于每个决策器的训练上,对于第k个决策器的训练,Adboost的训练方法是把决策器D(k)和系数a(k)拆开训练,先训练D(k),后训练系数a(k)。
1.1.4 算法流程

第一步:初始化样本权重
初始化训练数据(每个样本)的权值分布。每一个训练样本,初始化时赋予同样的权值w=1/N。N为样本总数。
权值分布 D 1 = ( w 11 , w 12 , . . . , w 1 i . . . , w 1 N ) , w 1 i = 1 N D 1 表示,第一次迭代每个样本的权值。 w 11 表示,第 1 次迭代时的第一个样本的权值。 N 为样本总数。 权值分布D_1 = (w_{11},w_{12},...,w_{1i}...,w_{1N}),w_{1i} =\frac{1}{N} \\ D_1表示,第一次迭代每个样本的权值。w_{11}表示,第1次迭代时的第一个样本的权值。N为样本总数。 权值分布D1=(w11,w12,...,w1i...,w1N),w1i=N1D1表示,第一次迭代每个样本的权值。w11表示,第1次迭代时的第一个样本的权值。N为样本总数。
第二步:进行多次迭代
a ) 使用具有权值分布 D m ( m = 1 , 2 , 3 … N ) 的训练样本集进行学习,得到弱的分类器。 G m ( x ) 取值为 − 1 , 1 意思是,第 m 次迭代时的弱分类器,将样本 x 要么分类成 − 1 ,要么分类成 1. 那么根据什么准则得到弱分类器? 准则为:该弱分类器的误差函数最小,也就是【分错的样本对应的权值之和】最小。 ε m = ∑ i = 1 N w n m I ( y m ( x n ) ≠ t n ) b ) 计算弱分类器 G m ( x )的话语权,话语权 a m 表示 G m ( x )在最终分类器中的重要程度。其中 e m ,为上步中的 ε m (误差函数的值) a m = 1 2 ln 1 − e m e m 该式是随 e m 减小而增大。即误差率小的分类器,在最终分类器的重要程度大。 c )更新训练样本集的权值分布。用于下一轮迭代。其中,被误分的样本的权值会增大,被正确分的权值减小。 D m + 1 = ( w m + 1 , 1 , w m + 1 , 2 , . . . , w m + 1 , i . . . , w m + 1 , N ) ) 公式 : w m + 1 , i = w m , i Z m e − a m y i G m ( x i ) , i = 1 , 2 , . . . , N Z m = ∑ i = 1 N w m , i e − a m y i G m ( x i ) ,是保证权重和为 1 a)使用具有权值分布D_m(m=1,2,3…N)的训练样本集进行学习,得到弱的分类器。\\ G_m(x)取值为{-1,1} \\ 意思是,第m次迭代时的弱分类器,将样本x要么分类成-1,要么分类成1.那么根据什么准则得到弱分类器?\\ 准则为:该弱分类器的误差函数最小,也就是【分错的样本对应的 权值之和】最小。\\ ε_m=\sum\limits_{i=1}^Nw_{n}^mI(y_m(x_n) \neq t_n ) \\ b)计算弱分类器G_m(x)的话语权,话语权a_m表示G_m(x)在最终分类器中的重要程度。其中e_m,为上步中的ε_m(误差函数的值)\\ a_m = \frac{1}{2}\ln\frac{1-e_m}{e_m} \\ 该式是随e_m减小而增大。即误差率小的分类器,在最终分类器的 重要程度大。\\ c)更新训练样本集的权值分布。用于下一轮迭代。其中,被误分的样本的权值会增大,被正确分的权值减小。\\ D_{m+1} = (w_{m+1,1},w_{m+1,2},...,w_{m+1,i}...,w_{m+1,N}))\\ 公式:w_{m+1,i} = \frac{w_{m,i}}{Z_m}e^{-a_my_iG_m(x_i)},i=1,2,...,N \\ Z_m=\sum\limits_{i=1}^Nw_{m,i}e^{-a_my_iG_m(x_i)},是保证权重和为1 a)使用具有权值分布Dm(m=1,2,3…N)的训练样本集进行学习,得到弱的分类器。Gm(x)取值为−1,1意思是,第m次迭代时的弱分类器,将样本x要么分类成−1,要么分类成1.那么根据什么准则得到弱分类器?准则为:该弱分类器的误差函数最小,也就是【分错的样本对应的权值之和】最小。εm=i=1∑NwnmI(ym(xn)=tn)b)计算弱分类器Gm(x)的话语权,话语权am表示Gm(x)在最终分类器中的重要程度。其中em,为上步中的εm(误差函数的值)am=21lnem1−em该式是随em减小而增大。即误差率小的分类器,在最终分类器的重要程度大。c)更新训练样本集的权值分布。用于下一轮迭代。其中,被误分的样本的权值会增大,被正确分的权值减小。Dm+1=(wm+1,1,wm+1,2,...,wm+1,i...,wm+1,N))公式:wm+1,i=Zmwm,ie−amyiGm(xi),i=1,2,...,NZm=i=1∑Nwm,ie−amyiGm(xi),是保证权重和为1
第三步:迭代完成后,组合弱分类器
f ( x ) = ∑ m = 1 N a m G m ( x ) 然后,加个 s i g n 函数,该函数用于求数值的正负。得到最终的强分类器 G ( x ) G ( x ) = s i g n ( f ( x ) ) f(x)=\sum\limits_{m=1}^Na_{m}G_m(x) \\ 然后,加个sign函数,该函数用于求数值的正负。得到最终的强分类器G(x)\\ G_{(x)} = sign(f(x)) f(x)=m=1∑NamGm(x)然后,加个sign函数,该函数用于求数值的正负。得到最终的强分类器G(x)G(x)=sign(f(x))
迭代终止条件:
(1)如果当前决策器的训练效果不佳,例如em过大
(2)如果当前Adboost的效果已经很好
(3)达到最大决策器个数
1.2 实际案例解释Adaboost算法流程
给定如下表所示训练数据。假设个体学习器由x(输入)和y(输出)产生,其阈值v(判定正反例的分界线)使该分类器在训练数据集上分类误差率最低。(y=1为正例,y=-1为反例)
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 |
1.2.1 第一个个体学习器
我们首先认为xi(i=1,2,…,10)的权重是一样的,即每一个数据同等重要。(权重是用来计算误差的)

( a ) :在权值分布为 D 1 的训练数据上,阈值 v 取 2.5 (红线)时分类误差率最低。 此时 x = 6 , 7 , 8 的数据被错分为反例,误差为它们的权重之和 e 1 = 0.1 + 0.1 + 0.1 = 0.3 ,误差率小于 0.5 才有意义。 此时,个体学习器为 : G 1 ( x ) = { 1 , x<2.5 − 1 , x>2.5 ( b ) : 根据误差 e 1 ,利用公式: a i = 1 2 ln 1 − e i e i ,计算系数 a 1 = 0.4236 。 可以发现只有当 e i < 1 2 ,此时的个体学习器才有意义。 ( c ) :更新训练数据的权值分布。 公式 : w m + 1 , i = w m , i Z m e − a m y i G m ( x i ) , i = 1 , 2 , . . . , N Z m = ∑ i = 1 N w m , i e − a m y i G m ( x i ) ,是保证权重和为 1 (a):在权值分布为D_1的训练数据上,阈值v取2.5(红线)时分类误差率最低。\\ 此时x=6,7,8的数据被错分为反例,误差为它们的权重之和e_1=0.1+0.1+0.1=0.3,误差率小于0.5才有意义。\\ 此时,个体学习器为: \\ G_1(x) = \begin{cases} 1, & \text{x<2.5}\\ -1,& \text{x>2.5} \end{cases} \\ (b):根据误差e_1,利用公式:a_i = \frac{1}{2}\ln\frac{1-e_i}{e_i},计算系数a_1=0.4236。\\ 可以发现只有当e_i<\frac{1}{2},此时的个体学习器才有意义。\\ (c):更新训练数据的权值分布。\\ 公式:w_{m+1,i} = \frac{w_{m,i}}{Z_m}e^{-a_my_iG_m(x_i)},i=1,2,...,N \\ Z_m=\sum\limits_{i=1}^Nw_{m,i}e^{-a_my_iG_m(x_i)},是保证权重和为1 (a):在权值分布为D1的训练数据上,阈值v取2.5(红线)时分类误差率最低。此时x=6,7,8的数据被错分为反例,误差为它们的权重之和e1=0.1+0.1+0.1=0.3,误差率小于0.5才有意义。此时,个体学习器为:G1(x)={1,−1,x<2.5x>2.5(b):根据误差e1,利用公式:ai=21lnei1−ei,计算系数a1=0.4236。可以发现只有当ei<21,此时的个体学习器才有意义。(c):更新训练数据的权值分布。公式:wm+1,i=Zmwm,ie−amyiGm(xi),i=1,2,...,NZm=i=1∑Nwm,ie−amyiGm(xi),是保证权重和为1
我们用python来计算更新后的权重:
import numpy as np# 定义计算系数a值公式
def get_a(e):a = 0.5 * np.log((1-e) / e)return a# 定义个体学习器,预测y值,其中x为样本数据,v为阈值
def G(x,v):y = []for i in x:if i < v:y.append(1)else:y.append(-1)return y# 训练数据
x = [i for i in range(0,10)]
y = [1, 1, 1, -1, -1, -1, 1, 1, 1, -1]# 原始的权重为
w = [0.1,0.1,0.1,0.1,0.1, 0.1,0.1,0.1,0.1,0.1]
def update_w(w,a,y,y_pred):w_u = []for w_index,w_value in enumerate(w):r = w_value * np.exp(-a * y[w_index] * y_pred[w_index])w_u.append(r)return w_u / np.sum(w_u)# 误差权重和
e1 = 0.1 + 0.1 + 0.1
# 系数a
a = get_a(e1)
# 阈值v
v = 2.5
# 预测的y值
y_pred = G(x,v)# 更新权重
w = update_w(w,a,y,y_pred)
w.reshape(-1,10)

可以看到x=6,7,8的数据的权重变大了,而其他数据的权重降低了,这是希望能把之前经常分类错误(经常分类错误,权重会不断变大)的数据能在下一个个体学习器分类正确(记住:权重是用来计算误差的,为了降低误差,选择阈值时会倾向把权重大的分类正确)。

此时, f 1 ( x ) = a 1 G 1 ( x ) = 0.4236 G 1 ( x ) = { 0.4236 ∗ 1 , x<2.5 0.426 ∗ ( − 1 ) , x>2.5 集成学习器 ( 第一次集成 ) s i g n [ f 1 ( x ) ] = { 1 , x<2.5 − 1 , x>2.5 此时,f_1(x) = a_1G_1(x) =0.4236G_1(x)= \begin{cases} 0.4236*1, & \text{x<2.5}\\ 0.426*(-1),& \text{x>2.5} \end{cases}\\ 集成学习器(第一次集成)sign[f_1(x)] = \begin{cases} 1, & \text{x<2.5}\\ -1,& \text{x>2.5} \end{cases} 此时,f1(x)=a1G1(x)=0.4236G1(x)={0.4236∗1,0.426∗(−1),x<2.5x>2.5集成学习器(第一次集成)sign[f1(x)]={1,−1,x<2.5x>2.5
集成学习器(第一次集成,只有一个个体学习器)在训练数据集上有3个误分类点。
1.2.2 第二个个体学习器

( a ) :在权值分布为 D 2 的训练数据上,阈值 v 取 8.5 (红线)时分类误差率最低。 此时 x = 3 , 4 , 5 的数据被错分为反例,误差为它们的权重之和 e 2 = 0.2143 ,可以发现,误差率降低了。 此时,个体学习器为 : G 2 ( x ) = { 1 , x<8.5 − 1 , x>8.5 ( b ) : 根据误差 e 2 ,计算系数 a 2 = 0.6496 。 ( c ) :更新训练数据的权值分布。 (a):在权值分布为D_2的训练数据上,阈值v取8.5(红线)时分类误差率最低。\\ 此时x=3,4,5的数据被错分为反例,误差为它们的权重之和e_2=0.2143,可以发现,误差率降低了。\\ 此时,个体学习器为: \\ G_2(x) = \begin{cases} 1, & \text{x<8.5}\\ -1,& \text{x>8.5} \end{cases} \\ (b):根据误差e_2,计算系数a_2=0.6496。\\ (c):更新训练数据的权值分布。 (a):在权值分布为D2的训练数据上,阈值v取8.5(红线)时分类误差率最低。此时x=3,4,5的数据被错分为反例,误差为它们的权重之和e2=0.2143,可以发现,误差率降低了。此时,个体学习器为:G2(x)={1,−1,x<8.5x>8.5(b):根据误差e2,计算系数a2=0.6496。(c):更新训练数据的权值分布。
我们继续用python来计算更新后的权重:
# 误差权重和
e2 = 0.2143
# 系数a
a2 = get_a(e2)
# 阈值v
v = 8.5
y_pred = G(x,v)# 更新权重
w = update_w(w,a2,y,y_pred)
w.reshape(-1,10)

对比权重D2可以看到x=3,4,5的数据的权重变大了,而其他权重降低了。


1.2.3 第三个个体学习器

( a ) :在权值分布为 D 3 的训练数据上,阈值 v 取 5.5 (红线)时分类误差率最低。 此时 x = 0 , 1 , 2 , 9 的数据被错分为反例,误差为它们的权重之和 e 3 = 0.1820 ,可以发现,误差率又降低了。 此时,个体学习器为 : G 3 ( x ) = { 1 , x<5.5 − 1 , x>5.5 ( b ) : 根据误差 e 3 ,计算系数 a 3 = 0.7514 。 ( c ) :更新训练数据的权值分布。 (a):在权值分布为D_3的训练数据上,阈值v取5.5(红线)时分类误差率最低。\\ 此时x=0,1,2,9的数据被错分为反例,误差为它们的权重之和e_3=0.1820,可以发现,误差率又降低了。\\ 此时,个体学习器为: \\ G_3(x) = \begin{cases} 1, & \text{x<5.5}\\ -1,& \text{x>5.5} \end{cases} \\ (b):根据误差e_3,计算系数a_3=0.7514。\\ (c):更新训练数据的权值分布。 (a):在权值分布为D3的训练数据上,阈值v取5.5(红线)时分类误差率最低。此时x=0,1,2,9的数据被错分为反例,误差为它们的权重之和e3=0.1820,可以发现,误差率又降低了。此时,个体学习器为:G3(x)={1,−1,x<5.5x>5.5(b):根据误差e3,计算系数a3=0.7514。(c):更新训练数据的权值分布。
# 误差权重和
e3 = 0.1820
# 系数a
a3 = get_a(e3)
# 阈值v
v = 5.5
y_pred = G(x,v)print(a3)# 更新权重
w = update_w(w,a3,y,y_pred)
w.reshape(-1,10)

此时,我们集成学习器表达式:


我们发现此时的集成学习器,在训练数据集上有0个误分类点。
总结如下
对比三个个体学习器我们可以发现,权值很低的数据从侧面说明,它们在前面的学习器经常被分类正确,也就是说它们被分类正确的票数就比较多(α相当于每个分类器的票数),那么之后的个体学习器把它们分类错也没所谓,反正总票数是分类正确的票数多就可以了。
-
例如x=1,前面两次分类对了,获得正确票数0.4236+0.6496=1.0732,第三次错了,获得错误票数0.7514,正确票数多,最终还是分类正确了。为了想办法让分类错误的数据变为分类正确的,后面的个体学习器也在努力。
-
如x=6,第一次分类错误的票数为0.4236,第二次分类正确的票数0.6496,可以看到为了让前面分类错误的数据变为分类正确的,后面个体学习器的重要性(α)需要比前面的大。
1.3 Adaboost算法原理
1.3.1 加法模型
预测函数

类比Adaboost的预测函数,可以知道Adaboost是一个加法模型。
损失函数
回归问题:MSE均方误差
分类问题:指数函数、交叉熵损失
优化方法

使用【前向分布算法】进行优化。
1.3.2 算法原理
1、优化问题:二分类问题
二分类的标签为{-1,1}。注:一定是{-1,1},不能是{0,1}
2、模型:加法模型
f ( x ) = ∑ m = 1 M a m G m ( x ) f(x)=\sum\limits_{m=1}^Ma_{m}G_m(x) \\ f(x)=m=1∑MamGm(x)
3、最终分类器
G ( x ) = s i g n [ f ( x ) ] G(x)=sign[f(x)] G(x)=sign[f(x)]
4、损失函数:指数损失函数
L ( y , f ( x ) ) = e [ − y f ( x ) ] 当 G ( x ) 分类正确时候,与 y 同号, L ( y , f ( x ) ) < = 1 , 即损失是一个比较小的数 当 G ( x ) 分类错误时候,与 y 异号, L ( y , f ( x ) ) > 1 ,即损失是一个比较大的数 将损失函数视为训练数据的【权值】 w m i = e [ − y i f m − 1 ( x i ) ] L(y,f(x)) = e^{[-yf(x)]} \\ 当G(x)分类正确时候,与y同号,L(y,f(x))<=1 ,即损失是一个比较小的数\\ 当G(x)分类错误时候,与y异号,L(y,f(x))>1,即损失是一个比较大的数 \\ 将损失函数视为训练数据的【权值】\\ w_{mi}=e^{[-y_if_{m-1}(x_i)]} L(y,f(x))=e[−yf(x)]当G(x)分类正确时候,与y同号,L(y,f(x))<=1,即损失是一个比较小的数当G(x)分类错误时候,与y异号,L(y,f(x))>1,即损失是一个比较大的数将损失函数视为训练数据的【权值】wmi=e[−yifm−1(xi)]

5、优化算法:前向分布算法

极小化损失函数的公式准换

准换公式推导如下

求解转换后的公式
1、优化Gm(x)

2、优化am
a m = 1 2 ln 1 − e m e m a_m = \frac{1}{2}\ln\frac{1-e_m}{e_m} am=21lnem1−em
公式推导:
首先,将准换后的最小化损失函数的公式,再次进行准换

上式中,只有am为变量,对于此凸优化问题,可以对am求导

令求导后的公式为0

然后,对于分子分母,再除以所有样本的权值之和,进行化简,可以得到公式
a m = 1 2 ln 1 − e m e m a_m = \frac{1}{2}\ln\frac{1-e_m}{e_m} am=21lnem1−em
3、前向更新fm(x)
f m ( x ) = f m − 1 ( x ) + a m G m ( x ) f_m(x)=f_{m-1}(x) + a_mG_m(x) fm(x)=fm−1(x)+amGm(x)
4、更新训练数据权值
公式 : w m + 1 , i = w m , i Z m e − a m y i G m ( x i ) , i = 1 , 2 , . . . , N Z m = ∑ i = 1 N w m , i e − a m y i G m ( x i ) ,是保证权重和为 1 公式:w_{m+1,i} = \frac{w_{m,i}}{Z_m}e^{-a_my_iG_m(x_i)},i=1,2,...,N \\ Z_m=\sum\limits_{i=1}^Nw_{m,i}e^{-a_my_iG_m(x_i)},是保证权重和为1 公式:wm+1,i=Zmwm,ie−amyiGm(xi),i=1,2,...,NZm=i=1∑Nwm,ie−amyiGm(xi),是保证权重和为1
公式推导如下(未归一化)

本篇笔记主要参考如下:
李航老师的<学习统计方法>
https://blog.csdn.net/fuqiuai/article/details/79482487
http://ml.bbbdata.com/site/text/100
相关文章:

传统机器学习(六)集成算法(2)—Adaboost算法原理
传统机器学习(六)集成算法(2)—Adaboost算法原理 1 算法概述 Adaboost(Adaptive Boosting)是一种自适应增强算法,它集成多个弱决策器进行决策。 Adaboost解决二分类问题,且二分类的标签为{-1,1}。注:一定是{-1,1},不能是{0,1} …...

性能优化常用的技巧,你都知道吗?
在实际工作中,提升MySQL数据库的查询性能是非常重要的。除了基本的索引和查询优化技巧外,还有一些更深层次的优化方案可以进一步优化性能。 1. 数据库表设计优化 选择字段类型: 根据数据类型和范围,选择适当的字段类型。例如&am…...
机器学习——损失函数(lossfunction)
问:非监督式机器学习算法使用样本集中的标签构建损失函数。 答:错误。非监督式机器学习算法不使用样本集中的标签构建损失函数。这是因为非监督式学习算法的目的是在没有标签的情况下发现数据集中的特定结构和模式,因此它们依赖于不同于监督式…...
小航助学2022年NOC初赛图形化(小高组)(含题库答题软件账号)
需要在线模拟训练的题库账号请点击 小航助学编程在线模拟试卷系统(含题库答题软件账号)_程序猿下山的博客-CSDN博客 单选题3.0分 删除编辑 答案:C 第1题如果要控制所有角色一起朝舞台区右侧移动,下面哪个积木块是不需要的? A…...
软考中级数据库系统工程师-第6-7章 数据库技术基础关系数据库
目录 1.数据库系统基本概念 2.数据库系统的三级模式结构 3.两级映像 4.数据的独立性 5.E-R模型 6.关系的相关名词 7.关系代数运算 8.关系数据库设计基础知识 9.规范化 1.数据库系统基本概念 1)数据库系统(DBS)是一个采用了数据库技术,有组织地、…...

掌握RDD算子2
文章目录 扁平映射算子案例任务1、统计不规则二维列表元素个数方法一、利用Scala来实现方法二、利用Spark RDD来实现 按键归约算子案例任务1、在Spark Shell里计算学生总分任务2、在IDEA里计算学生总分第一种方式:读取二元组成绩列表第二种方式:读取四元…...
)
ORACLE-SQL性能优化(3)
2. 给优化器更明确的命令 自动选择索引 如果表中有两个以上(包括两个)索引,其中有一个唯一性索引,而其他是非唯一性. 在这种情况下,ORACLE将使用唯一性索引而完全忽略非唯一性索引. 举例: SELEC…...

3年外包裸辞,面试阿里、字节全都一面挂,哭死.....
测试员可以先在外包积累经验,以后去大厂就很容易,基本不会被卡,事实果真如此吗?但是在我身上却是给了我很大一巴掌... 所谓今年今天履历只是不卡简历而已,如果面试答得稀烂,人家根本不会要你。况且要不是大…...
 -- 多线程(信号量与CountDownLatch))
JavaEE(系列16) -- 多线程(信号量与CountDownLatch)
目录 1. 信号量Semaphore 2. CountDownLatch 1. 信号量Semaphore 信号量, 用来表示 "可用资源的个数". 本质上就是一个计数器. 1.理解信号量 可以把信号量想象成是停车场的展示牌: 当前有车位 100 个. 表示有 100 个可用资源.当有车开进去的时候, 就相当于申请一个可…...
Tomcat配置https协议证书-阿里云,Nginx配置https协议证书-阿里云,Tomcat配置https证书pfx转jks
Tomcat/Nginx配置https协议证书 前言Tomcat配置https协议证书-阿里云方式一 pfx配置证书重启即可 方式二 jkspfx生成jks配置证书重启即可 Nginx配置https协议证书-阿里云实现方式重启即可 其他Tomcat相关配置例子如下nginx配置相关例子如下 前言 阿里云官网:https:…...

抖音定位基本原理
抖音是一款非常受欢迎的短视频分享应用程序,它允许用户创建和分享15秒到60秒的短视频。抖音的成功在很大程度上归功于其强大的定位技术,该技术可以根据用户的兴趣和位置提供个性化的内容。在本文中,我们将深入探讨抖音的定位技术,…...

【Hbase 05】Hbase表的设计原则与优化方案
这里说一下Hbase在使用过程中的表设计原则与优化方案,如果你是运维或者开发兼顾环境的工作,也许比较受用,话不多说,我们直接开始说优化的内容: 一、表设计原则 1.行键设计 行键在设计的时候要尽量的散列,例如可以考虑使用哈希、加密算法等使结果散列,这样能保证请求不会…...
行业报告 | 2022文化科技十大前沿应用趋势(上)
文 | BFT机器人 前言 Introduction 文化科技是文化科技融合过程中诞生的系列新技术成果,是文化强国和科技强国两大战略的交又领域。2012 年 8月,科技部会同中宣部、财政部、文化部、广电总局、新闻出版总署发布《文化科技创新工程纲要》,开启…...
实现BIM的Revit软件学习资料
实现BIM的Revit软件学习资料 一、BIM与Revit的关系二、Revit使用方法总结(一)快捷键(二)一些技巧 一、BIM与Revit的关系 链接: BIM与Revit是什么关系?看完秒懂系列! REVIT是实现BIM理念的工具之一。 二、Revit使用方…...

09 集合框架2
集合元素的迭代方式有哪些? for循环,for-each循环(底层迭代器),迭代器 Iterator<String> it list.iterator(); while(it.hasNext()) {String ele it.next();System.out.println(ele); }并发修改集合元素异常是怎么造成的?怎么解决? 在迭代过程中使用List里面的增…...

相见恨晚的5款良心软件,每款都是经过时间检验的精品
今天来给大家推荐5款良心软件,每款都是经过时间检验的精品,用起来让你的工作效率提升飞快,各个都让你觉得相见恨晚! 1.颜色选择器——ColorPicker ColorPicker是一款用于在屏幕上选择颜色的工具。它可以让你快速地获取任意像素的颜色值,并复制到剪贴板…...
AI与税务管理:新技术带来的新机遇和新挑战
本文作者:王伊琳 人工智能(Artificial Intelligence,AI)是指由计算机系统或机器人模拟人类智能的过程和结果,包括感知、理解、学习、推理、决策等能力。近年来,随着计算机技术、互联网平台、大数据分析等的…...
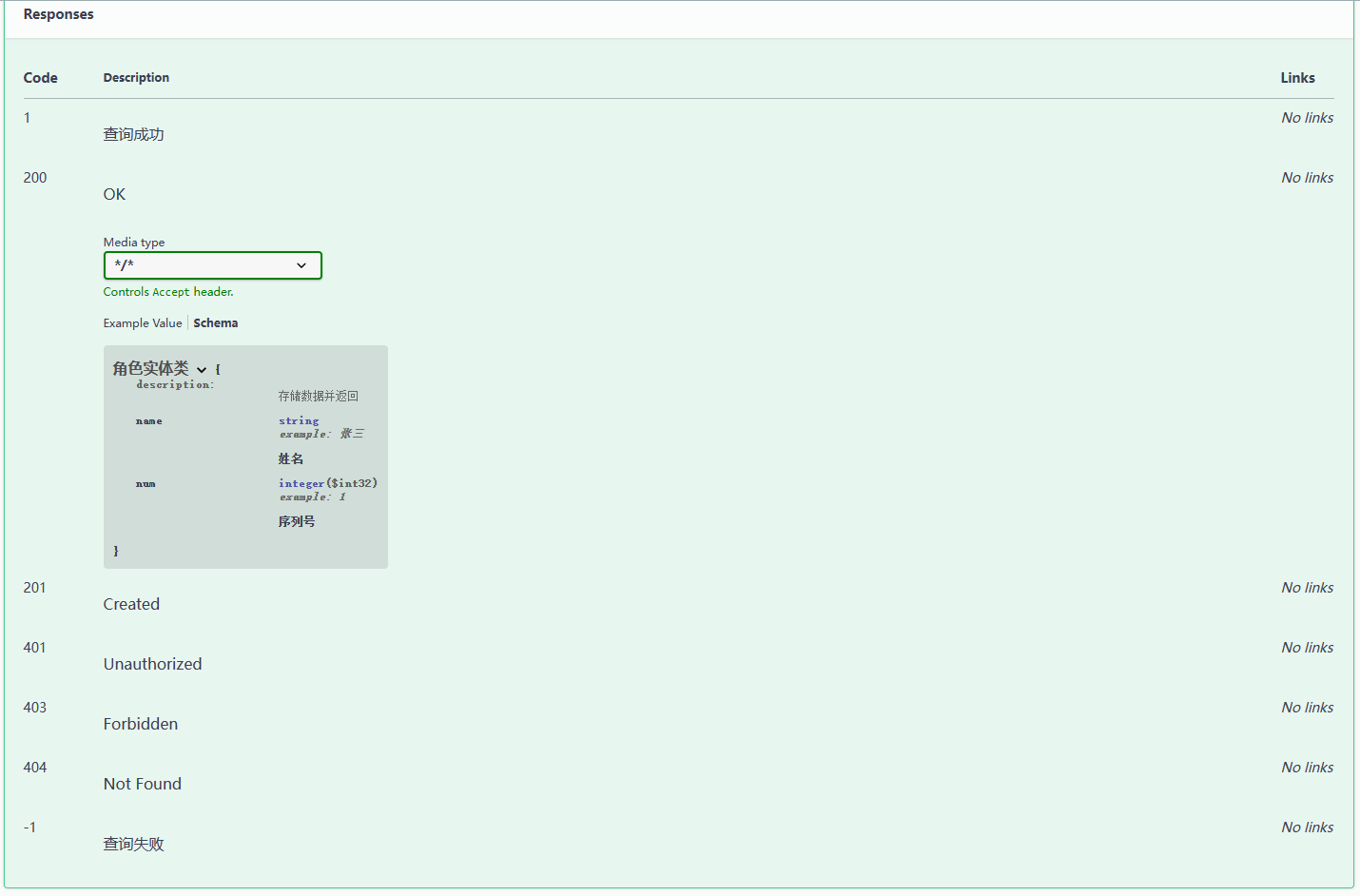
springboot 集成 Swagger3(速通)
→ springboot 集成 Swagger2 ← 目录 1. 案例2. info 配置3. Docket 配置1. 开关配置2. 扫描路径3. 路径匹配4. 分组管理 4. 常用注解1. 说明2. 案例 1. 案例 这次直接使用 2.5.6 的 spring-boot 。 依赖: <parent><groupId>org.springframework.…...
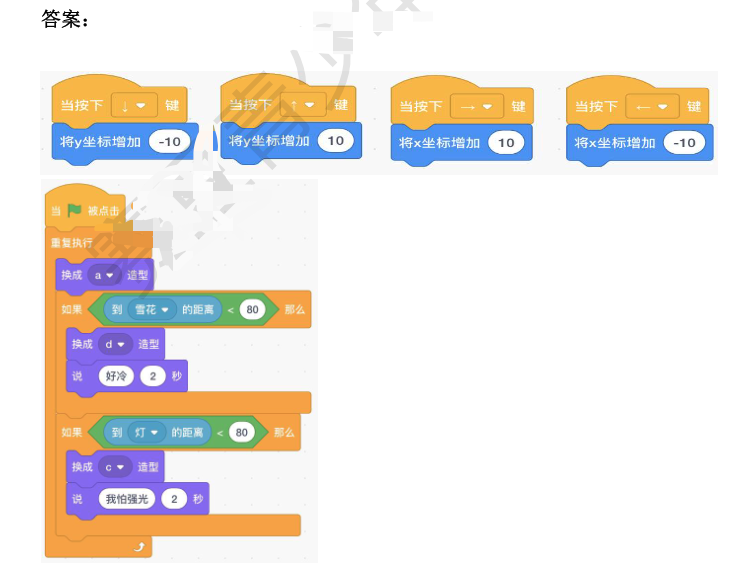
2023年NOC大赛创客智慧编程赛项图形化复赛模拟题二,包含答案解析
2023年NOC大赛创客智慧编程赛项图形化复赛模拟题二,包含答案解析 第一题: 在源程序“小蝙蝠”文件中,实现小蝙蝠遇到不同的角色会说不同的话,以及切换不同的造型要求: 1:游戏开始时,小蝙蝠角色是造型 a,并能够用键盘控制上、下、左、右移动; 2:移动小蝙蝠,距离角色雪…...

2023年NOC大赛创客智慧编程赛项Python 复赛模拟题(二)
题目来自:NOC 大赛创客智慧编程赛项Python 复赛模拟题(二) NOC大赛创客智慧编程赛项Python 复赛模拟题(二) 第一题: 编写一个成绩评价系统,当输入语文、数学和英语三门课程成绩时,输出三门课程总成绩及其等级。 (1)程序提示用户输入三个数字,数字分别表示语文、数学、…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
