Leetcode:198. 打家劫舍、213. 打家劫舍 II、337. 打家劫舍 III(C++)
目录
198. 打家劫舍
问题描述:
实现代码与解析:
动态规划(版本一):
原理思路:
动态规划(版本二):
原理思路:
213. 打家劫舍 II
问题描述:
实现代码与解析:
动态规划:
原理思路:
337. 打家劫舍 III
问题描述:
实现代码与解析:
动态规划(树形dp):
原理思路:
198. 打家劫舍
问题描述:
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1] 输出:4 解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1] 输出:12 解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。偷窃到的最高金额 = 2 + 9 + 1 = 12 。
实现代码与解析:
动态规划(版本一):
class Solution {
public:int rob(vector<int>& nums){//先把前两个单独弄出来返回if (nums.size() == 0) return 0;if (nums.size() == 1) return nums[0];//dp含义, 按顺序偷第 i 个屋子时获得的最大金额vector<int> dp(nums.size(), 0);//dp数组dp[0] = nums[0]; // 初始化dp[1] = nums[1];//遍历for (int i = 2; i < nums.size(); i++){//小于 3 的时候只能跳一个,所以单独计算一下喽if (i < 3) dp[i] = dp[i - 2] + nums[i];else{//跳一个或则跳两个,不能再多跳了,不然肯定会少偷,这两之间取最大喽dp[i] = max(dp[i - 2] + nums[i], dp[i - 3] + nums[i]);// 偷 i - 2的屋子时获得的最大金额,加上此屋子的金额,和偷 i - 3 的屋子时获得的最大金额加上此屋子金额取最大}}int result = max(dp[nums.size() - 1], dp[nums.size() - 2]);//倒数第一个和倒数第二个比较,因为最后偷的肯定是这两个房间之一return result;}
};原理思路:
这里dp数组的含义是偷第 i 个屋子后能获得的最大价值,有点像爬梯子,大家看注释就能懂,但是其实是写的麻烦了,所以大家看版本二就可以了,要简洁很多。
动态规划(版本二):
class Solution {
public:int rob(vector<int>& nums){//先把前两个单独弄出来返回if (nums.size() == 0) return 0;if (nums.size() == 1) return nums[0];//dp含义, 按顺序选择0~i的屋子是否偷取时获得的最大金额vector<int> dp(nums.size(), 0);//dp数组//初始化dp[0] = nums[0];dp[1] = max(nums[0], nums[1]);for(int i = 2; i < nums.size(); i++){dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);}return dp[nums.size() - 1];}
};原理思路:
这里dp数组的含义是在1 ~ i 之间选择能获取的最大金额。
所以房间有两种状态,一种是偷,那么我们就找出 i - 1 能获取的最大金额,然后加上 nums[ i ]就为此时的如果偷的最大金额,一种是不偷,那么我们肯定是偷了 i - 1 编号的房间,此时dp[ i - 1] 为不偷的最大价值,两个之间进行比较,就求出了对于 i 房间偷或不偷选择出的最大金额,也就是dp[ i ]了。
213. 打家劫舍 II
问题描述:
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
示例 1:
输入:nums = [2,3,2] 输出:3 解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
示例 2:
输入:nums = [1,2,3,1] 输出:4 解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
示例 3:
输入:nums = [1,2,3] 输出:3
实现代码与解析:
动态规划:
class Solution {
public:int robRange(vector<int>& nums,int start,int end){if(start == end) return nums[start];// 只有一种元素vector<int> dp(nums.size());dp[start] = nums[start]; // 初始化dp[start + 1] = max(nums[start], nums[start + 1]);for(int i = start + 2; i <= end; i++){dp[i] = max(dp[i - 1], dp[i - 2] + nums[i]);}return dp[end];}int rob(vector<int>& nums) {if(nums.size() == 0) return 0;if(nums.size() == 1) return nums[0];int result1 = robRange(nums, 0, nums.size() - 2); // 不选取最后有一个房间的最大价值int result2 = robRange(nums, 1, nums.size() - 1); // 不选取第一个房间的最大价值int result = max(result1, result2);return result;}
};原理思路:
相比于打家劫舍Ⅰ了一个限制条件,就是房屋练成环了,所以无非就两种情况,一种是首尾两个房间都不偷,一种是首尾两个房间偷其中一个,根据Ⅰ的思路我们只要算出,不选取最后一个房间的最大金额和不选取第一个房间的最大金额,两个之中取最大就可以了,所以就比Ⅰ多了个选最大的操作而已,其他相似照着写就行。
337. 打家劫舍 III
问题描述:
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
示例 1:
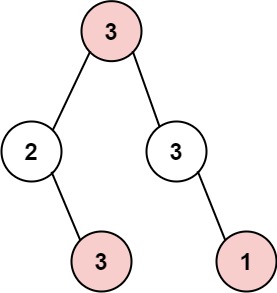
输入: root = [3,2,3,null,3,null,1] 输出: 7 解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7
示例 2:
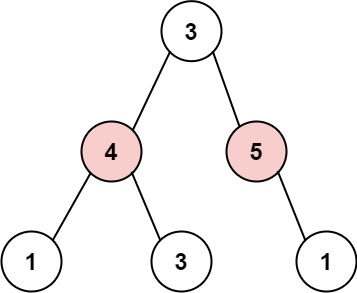
输入: root = [3,4,5,1,3,null,1] 输出: 9 解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9s
实现代码与解析:
动态规划(树形dp):
class Solution {
public://dp数组含义,0为不偷cur房间,1为偷cur房间vector<int> robTree(TreeNode* cur){//没有房间,返回0if(cur == NULL) return vector<int>{0,0};//左右子树偷或不偷的最大金额vector<int> leftDp = robTree(cur -> left);vector<int> rightDp = robTree(cur -> right);int value1 = leftDp[0] + rightDp[0] + cur -> val;// 此房间偷,那么其子树肯定不偷int value2 = max(leftDp[0], leftDp[1]) + max(rightDp[0], rightDp[1]);//不偷cur,此时判断其左右子树偷或不偷的最大值,不要认为一定偷子树就为最大值,一定要比较一下return {value2, value1};}int rob(TreeNode* root) {vector<int> result = robTree(root);return max(result[0], result[1]);}
};原理思路:
这里房间的连接变为二叉树的连接方式了,题目描述还是相连接的不能一起偷。
这里我们的dp数组的含义就发生改变了,dp为一个长度为2的数组,dp[ 0 ]表示不偷当前房间的最大金额,dp[ 1 ]表示偷当前房间的最大金额,并且作为返回值。
首先偷当前房间的递推公式好写,偷此房间,那么其孩子结点一定不偷:
dp[ 1 ] = leftDp[0] + rightDp[0] + cur -> val;
而不偷当前房间的话,我们就要比较孩子结点偷或不偷的最大金额了,取最大,注意不要认为偷孩子结点就是最大金额,这是一个误区,一定要比较一下,万一孩子结点的孩子结点和大于孩子结点呢?此时的递推公式为:
dp[ 0 ] = max(leftDp[0], leftDp[1]) + max(rightDp[0], rightDp[1]);
还有就是这里肯定是后序遍历,我们要知道孩子结点的信息。
相关文章:

Leetcode:198. 打家劫舍、213. 打家劫舍 II、337. 打家劫舍 III(C++)
目录 198. 打家劫舍 问题描述: 实现代码与解析: 动态规划(版本一): 原理思路: 动态规划(版本二): 原理思路: 213. 打家劫舍 II 问题描述:…...

【每日随笔】手指训练 ( 手指训练作用 | 哪些人需要手指训练 | 手指操 | 手指康复训练器材 )
文章目录一、手指训练作用二、哪些人需要手指训练三、手指操四、手指康复训练器材产品需求探索 , 研究下手指训练的市场 , 前景 , 是否可以开发 ; 一、手指训练作用 手指训练作用 : 改善 上肢协调性手眼 协调性训练提高 手指 抓握 能力提高 手指 灵活性提高 上肢运动 准确性 和…...

ATR指标在外汇交易中的另类运用方法
当涉及到外汇交易时,有许多不同的指标可以使用。然而,ATR指标可能是一个被低估的工具,可以帮助您发现有利可图的交易机会。本文将介绍ATR指标是什么,如何使用它来识别价格波动和制定交易策略,以及如何在外汇市场中另辟…...

SQL Server 数据批量导出处理
在实际项目环境中,有时会遇到需要将大量数据(这里所指百万级别以上的数据量)从一台服务器迁移到另外一台数据库服务器的情况。SQL Server有很多方式可以进行数据迁移:备份还原、导入/导出数据、生成脚本(包含数据&…...
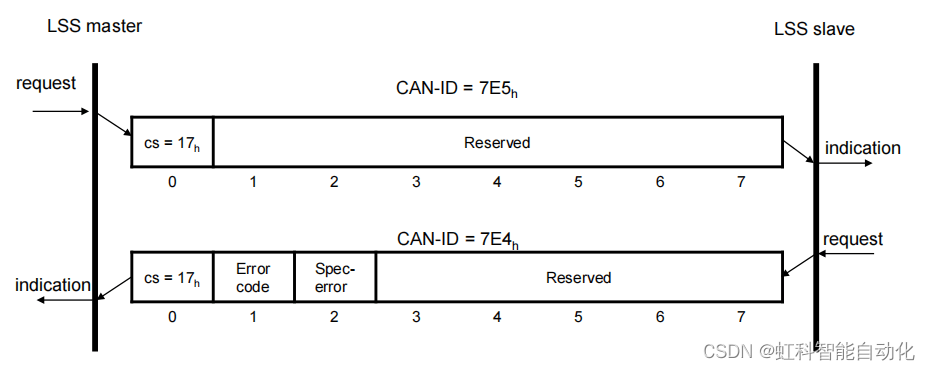
虹科分享 | CANopen协议基础知识——LSS服务
CANopen是一种架构在CAN串行总线系统上的高层通讯协议,常被用于嵌入式系统与工业控制领域,包括电机控制、机器人制造、医疗、汽车等多个行业领域。本篇文章将主要介绍CANopen的LSS服务。 一. LSS概述 Layer setting service (LSS)是CANopen的设置服务与…...

JS混淆和解混淆
在今天的数字时代,知识产权和商业机密对于企业的成功非常重要。JavaScript代码可以包含许多敏感信息,例如商业逻辑、客户数据和加密密钥。为了保护这些重要信息,JavaScript混淆和解混淆已经成为一种必要的技术。 什么是JavaScript混淆&#…...

MySQL-数值函数
绝对值函数语法格式:ABS(X)例:查看三个数值的绝对值(负的绝对值为它的正整数,0的绝对值为0,正的绝对值为它本身)。mysql> select abs(2),abs(-32),abs(-0.5); ----------------------------- | abs(2) |…...
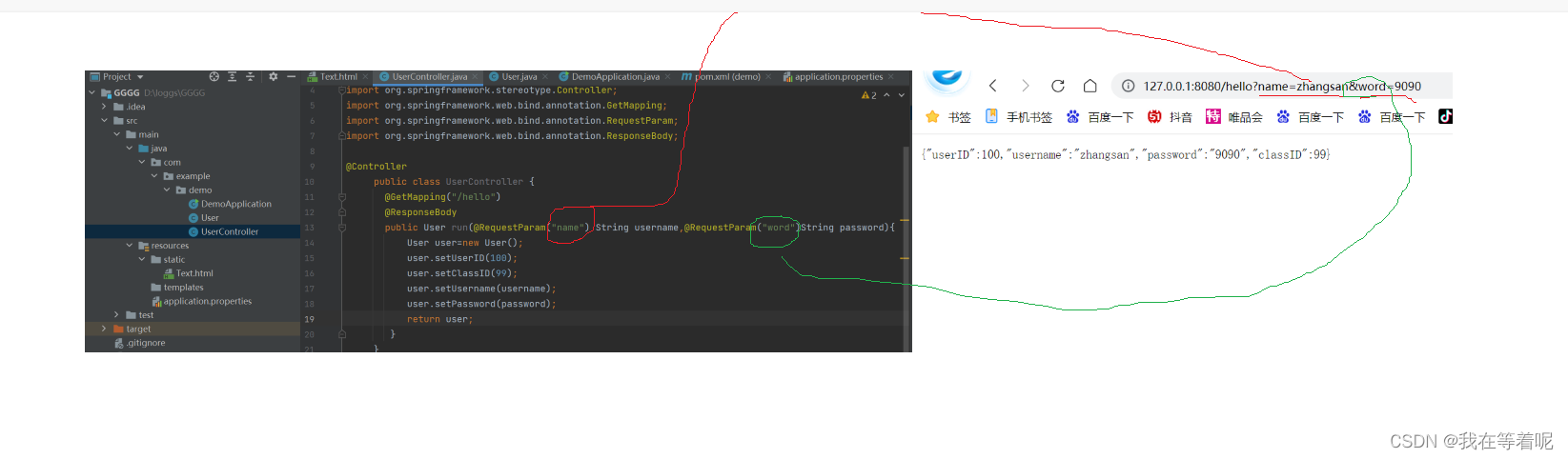
SpringMVC(1)
Web项目:基于HTTP协议,当一个用户从浏览器上面输入URL地址之后,URL能够和我们的程序映射起来,可以让用户的请求触达到后端程序里面,并且根据程序的处理,把结果返回浏览器; Spring MVC要进行学习的内容: 1)连…...

珠海先达MES系统六大功能解决电子组装行业可视化问题
电子组装行业的发展背景: 在日益激烈的市场环境中,降低成本,加快交付周期,提高产品质量已经成为了制造业发展的重要目标。企业关注的是产品的生产周期,客户关注的是产品的质量。如何在企业和消费者达成平衡,…...

获取本机的IP地址,看似简单的获取,实则蕴含非常多的操作
这篇文章讲述了PowerJob获取本地IP离奇曲折的经过,以及开放了诸多的可配置参数,打开了我新世界的大窗户。求个关注,求个点赞,求一个评论。 获取地址的操作,本来不应该作为什么重点,但是因为一点小小的意外&…...

【SSM】篇一:初试Spring--Ioc与Bean
文章目录1、Spring2、SpringFramework系统架构3、BeanBean的配置Bean的实例化Bean的生命周期4、依赖注入DIsetter注入和构造器注入依赖自动装配5、集合注入1、Spring Spring地址:https://spring.io Spring技术的优点: Spring家族(Spring全家…...
)
华为OD机试真题Python实现【出租车计费】真题+解题思路+代码(20222023)
🔥系列专栏 华为OD机试(Python)真题目录汇总华为OD机试(JAVA)真题目录汇总华为OD机试(C++)真题目录汇总华为OD机试(JavaScript)真题目录汇总文章目录 🔥系列专栏题目输入输出示例一输入输出说明示例二输入输出说明...

Elasticsearch:如何修改 nested 字段的值
Nested 类型是 object 数据类型的特殊版本,它允许对象数组以一种可以彼此独立查询的方式进行索引。在内部,嵌套对象将数组中的每个对象索引为单独的隐藏文档,这意味着每个嵌套对象都可以使用 nested query 独立于其他对象进行查询。每个 nest…...

【JAVA】jdk8 Stream 排序精通
背景 jdk8的stream流能方便的排序,但是每次都要查资料,非常不方便,不确定,所以这次直接弄懂,不再迷茫。 转载请注明来源,创作不易,请多多支持。 基础排序 stream流 大家应该都比较熟悉了&…...

python的opencv操作记录12——Canny算子使用
文章目录Canny算子非极大值抑制非极大值抑制中的插值滞后阈值实际应用直接使用Canny算子使用膨胀先阈值分割Canny算子 上一篇说到,我在一个小项目里需要在一幅图像中提取一根试管里的两种液体的截面。为了达到这个目的使用传统图像里的区域分割技术,实际…...

Spark on hive Hive on spark
文章目录Spark on hive & Hive on sparkHive 架构与基本原理Spark on hiveHive on sparkSpark on hive & Hive on spark Hive 架构与基本原理 Hive 的核心部件主要是 User Interface(1)和 Driver(3)。而不论是元数据库&a…...
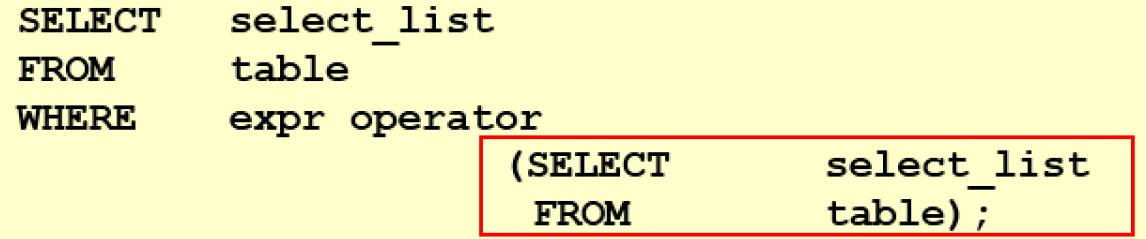
【MySQL】子查询
这里写自定义目录标题子查询1、子查询的基本使用2、 单行子查询2.1、单行比较查询2.2、HAVING 中的子查询2.3、CASE中的子查询3、多行子查询4、相关子查询5、EXISTS 与 NOT EXISTS关键字子查询 子查询指一个查询语句嵌套在另一个查询语句内部的查询,这个特性从MySQ…...

Day889.MySQL高可用 -MySQL实战
MySQL高可用 Hi,我是阿昌,今天学习记录的是关于MySQL高可用的内容。 正常情况下,只要主库执行更新生成的所有 binlog,都可以传到备库并被正确地执行,备库就能达到跟主库一致的状态,这就是最终一致性。但是…...

剑指 Offer 24. 反转链表
⭐简单说两句⭐ CSDN个人主页:后端小知识 🔎GZH:后端小知识 🎉欢迎关注🔎点赞👍收藏⭐️留言📝 题目: 剑指 Offer 24. 反转链表 ,我们今天还是来看一道easy的题目吧&…...
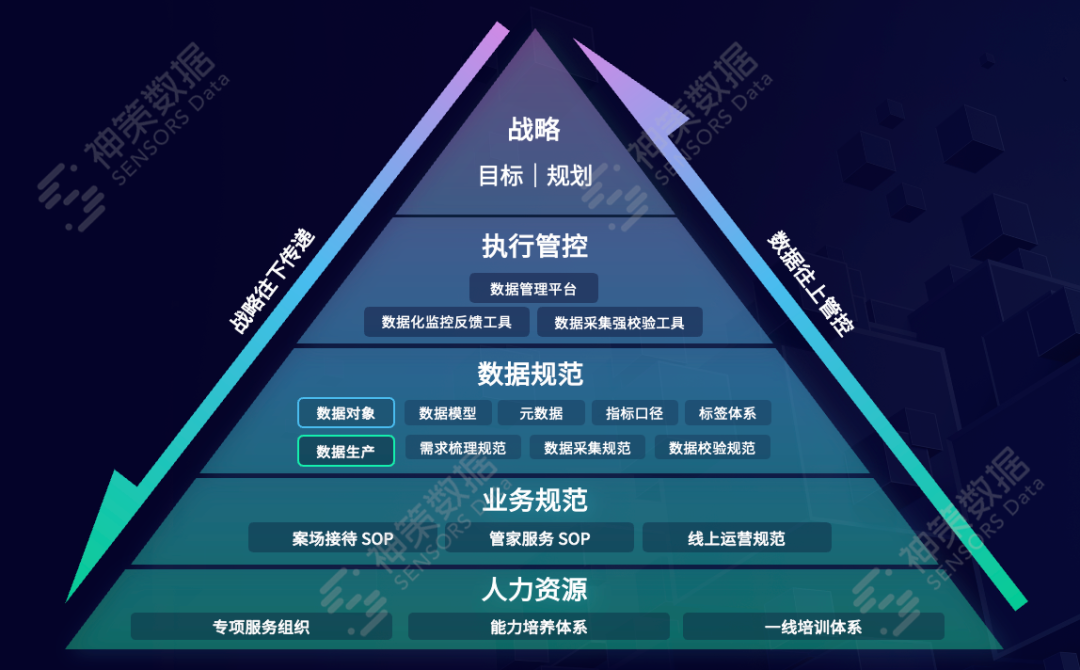
“黑铁时代”,地产人如何以客户视角加速房企数字化转型
本文从行业洞察、业务设计、数据建设以及实践探索四个部分详细阐述地产行业数字化的实践、思考和理解。点击文末“阅读原文”,观看完整版直播回放并下载演讲文档。一、洞察:房企经营思路的变化企业的转型都是围绕着业务经营变化进行的,房企数…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
