【C++、数据结构】哈希 — 闭散列与哈希桶的模拟实现
文章目录
- 📖 前言
- 1. STL中哈希表的两个应用⚡
- 1.1 🌟unordered_set
- 1.2 🌟unordered_map
- 2. 常见查找的性能对比💥
- 3. 哈希表模拟实现🏁
- 3.1 哈希的概念:
- 3.2 哈希函数:
- 3.3 哈希冲突:
- 3.4 闭散列 — 开放地址法:
- 3.5 开散列 — 哈希桶、拉链法,开链法:
📖 前言
哈希表在日常生活中我们一定略有耳闻,作为STL中我们所必须学习和了解的容器,首先哈希查找的时间复杂度为〇(1),是一种一一映射的存储方式,其次它在日常生活中的应用范围也是很广的,例如位图,海量数据筛选中用到的布隆过滤器等等……
下面我们就来先学习一下STL中的应用哈希表的两个容器,再了解一下底层结构 (两个关联式容器unordered_map和unordered_set,unordered系列的关联式容器之所以效率比较高,是因为其底层使用了哈希结构),最后再来模拟实现一下……
🙋 🙋 🙋 🙋 🙋
1. STL中哈希表的两个应用⚡
在STL中对应的容器分别是unordered_map和unordered_set这两个关联式容器。
只要我们会用set那么我们就会用unordered_set,但不是任何场景下,unordered_map/set都能将map/set替换掉。
哈希是一种映射,有的地方也叫散列:存储关键字跟存储位置建立关联关系
1.1 🌟unordered_set
unordered_set 文档介绍

我们简单的试用一下unordered_set,如下代码:
void test_set()
{unordered_set<int> s;//set<int> s;s.insert(1);s.insert(3);s.insert(4);s.insert(2);s.insert(10);//unordered_set<int>::iterator it = s.begin();auto it = s.begin();while (it != s.end()){cout << *it << " ";++it;}cout << endl;for (auto e : s){cout << e << " ";}cout << endl;
}

结果是无序的
由上图和查阅资料得知:
- map和set: 去重 + 排序
- unordered_map和unordered_set: 只有去重
其余函数接口和之前所学的容器使用起来大致相同,不再一一赘述。
unordered_map和unordered_set都是单向迭代器:
值得注意的是unordered_map和unordered_set的迭代器都是单项迭代器,而我们之前学的map和set则是单项迭代器。
unordered_set和set的性能对比:
void test_op()
{
//对比插入的效率:int n = 1000000;vector<int> v;v.reserve(n);srand(time(0));for (int i = 0; i < n; i++){//v.push_back(i);//v.push_back(rand()+i); //重复少v.push_back(rand()); //重复多}size_t begin1 = clock();set<int> s;for (auto e : v){s.insert(e);}size_t end1 = clock();size_t begin2 = clock();unordered_set<int> us;for (auto e : v){us.insert(e);}size_t end2 = clock();cout << s.size() << endl;cout << "set insert:" << end1 - begin1 << endl;cout << "unordered_set insert:" << end2 - begin2 << endl;//扩容重新哈希是有消耗的 -- 数据量多的时候,没有那么多重复的数据的时候也不一定//对比查找的效率size_t begin3 = clock();for (auto e : v){s.find(e);}size_t end3 = clock();size_t begin4 = clock();for (auto e : v){us.find(e);}size_t end4 = clock();cout << "set find:" << end3 - begin3 << endl;cout << "unordered_set find:" << end4 - begin4 << endl;//对比删除的效率size_t begin5 = clock();for (auto e : v){s.erase(e);}size_t end5 = clock();size_t begin6 = clock();for (auto e : v){us.erase(e);}size_t end6 = clock();cout << "set erase:" << end5 - begin5 << endl;cout << "unordered_set erase:" << end6 - begin6 << endl;
}
因为生成随机数的个数有个最大值,不能生成无限多个随机数,这就导致了有很多数字的重复。
当重复的数字很多时:

当没有重复的数字时:

总结:
总的来说unordered_map和unordered_set要比map和set的性能要好的,但是也并不是一定的,当数据量很大的时候,扩容重新哈希是有消耗的。
1.2 🌟unordered_map
unordered_map文档介绍

void test_map()
{unordered_map<string, string> dict;dict.insert(make_pair("sort", "排序"));dict.insert(make_pair("left", "左边"));dict.insert(make_pair("left", "剩余"));dict["string"];dict["left"] = "剩余";dict["string"] = "字符串";unordered_map<string, string>::iterator it = dict.begin();while (it != dict.end()){cout << (*it).first << " " << (*it).second << endl;it++;}
}

2. 常见查找的性能对比💥
-
暴力查找: 时间复杂度〇(N)
-
二分查找: 时间复杂度〇(logN) ,缺点 — 有序、数组结构
-
搜索二叉树: 时间复杂度〇(N),缺点 — 极端场景退化成单支
-
平衡二叉搜索树: 时间复杂度〇(logN)
-
- AVLTree: 左右子树高度差不超过1
-
- 红黑树:最长路径不超过最短路径的2倍
-
哈希
-
B树系列: 多叉平衡搜索树 — 数据库原理
-
跳表
备注:
红黑树高度略高一些,但是跟AVL树是同一数量级,对于现代计算机没有差别但是红黑树相对而言近似平衡,旋转少。

3. 哈希表模拟实现🏁
3.1 哈希的概念:
普通查找:
- 我们之前查找一个数据时,一般都是通过比较,查找一个元素时,必须要经过关键码的多次比较。顺序查找时间复杂度为〇(N),平衡树中为树的高度,即〇(logN)。
理想的搜索方法:
- 可以不经过任何比较,一次直接从表中得到要搜索的元素。
- 如果构造一种存储结构,通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立一一映射的关系,那么在查找时通过该函数可以很快找到该元素。
- 该中存储结构可以实现:
-
- 插入元素时:
根据待插入元素的关键码,以此函数计算出该元素的存储位置并按此位置进行存放。
- 插入元素时:
-
- 查找元素时:
对元素的关键码进行同样的计算,把求得的函数值当做元素的存储位置,在结构中按此位置
取元素比较,若关键码相等,则搜索成功。
- 查找元素时:
哈希表就由此而来…
3.2 哈希函数:
我们如何一一将键值转换为对应的关键码值,并映射到对应序号的存储位置呢?
直接映射法:
直接建立映射关系问题:
1、数据范围分布很广、不集中(可能存在空间浪费严重的问题)
2、key的数据不是整数,是字符串怎么办?是自定义类型对象怎么办?
此时我们就需要一个函数对特殊非整数类型的数据进行处理,使其返回一个特定的整数,这个函数我们叫做 —— 哈希函数。
常见的哈希函数:
- 直接定址法:(常用)
-
- 取关键字的某个线性函数为散列地址
-
- 使用场景:适合查找比较小且连续的情况
- 除留余数法:(常用)
-
- 直接用该值除以表的大小然后取余数
- 字符串哈希算法:(常用)
-
- 参考文献

- 参考文献
3.3 哈希冲突:
不同关键字通过相同哈希哈数计算出相同的哈希地址,该种现象称为哈希冲突或哈希碰撞。
按照上述哈希函数计算出键值对应的关键码值,但是算出来的这些码值当中,有很大的可能会出现关键码值相同的情况,这种情况就叫作:哈希冲突。
- 哈希函数设计的越精妙,产生哈希冲突的可能性就越低,但是无法避免哈希冲突。
- 解决哈希冲突两种常见的方法是:闭散列和开散列
3.4 闭散列 — 开放地址法:
闭散列: 也叫开放定址法,当发生哈希冲突时,如果哈希表未被装满,说明在哈希表中必然还有空位置,那么可以把key存放到冲突位置中的下一个空位置中去。
线性探测:(依次去找空位置)

从发生冲突的位置开始,依次向后探测,直到寻找到下一个空位置为止。
插入:
- 通过哈希函数获取待插入元素在哈希表中的位置
- 线性探测找到空位置将值插入
查找
- 挨个遍历哈希表,直到找到空为止
删除:
- 通过关键码值再用线性探测找到该值直接删除
- 注意:
-
- 删除要是直接删除的话有可能会影响查找的准确性
-
- 如图删除了10,要去找60就会找不到

- 如图删除了10,要去找60就会找不到
-
- 所以我们给每个键值提供一个状态,采取伪删除的方法

线性探测的缺点:
- 一旦发生哈希冲突,所有的冲突连在一起,容易产生数据“堆积”,即:不同关键码占据了可利用的空位置,使得寻找某关键码的位置需要许多次比较,导致搜索效率降低。
二次探测:(跳跃着找空位置)

对上面方法的优化:
- 不那么拥堵
闭散列哈希表并不能太满:
- 太满就会导致线性探测时,找不到位置
- 更不能放满,那样探测就会陷入死循环
- 所以要控制一下存储的数据
- 我们引入了一个变量
n来记录存储数据的个数
散列表的载荷因子定义为: a = 填入表中的元素个数 / 散列表的长度
所以我们要控制一下负载因子:

代码如下:
template<class K>
struct DefaultHash
{size_t operator()(const K& key){return (size_t)key;}
};//字符串哈希算法
template<>
struct DefaultHash<string>
{size_t operator()(const string& key){//BKDRsize_t hash = 0;for (auto ch : key){hash = hash * 131 + ch;}return hash;}
};//闭散列(开放地址法)
namespace CloseHash
{enum State{EMPTY,EXITS,DELETE};template<class K, class V>struct HashData{pair<K, V> _kv;State _state = EMPTY;};template<class K, class V, class HashFunc = DefaultHash<K>>class HashTable{typedef HashData<K, V> Data;public:bool Insert(const pair<K, V>& kv){//去重if (Find(kv.first)){return false;}//负载因子到0.7及以上,就扩容if (_tables.size() == 0 || _n * 10 / _tables.size() >= 7){size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;//扩容以后,需要重新映射HashTable<K, V, HashFunc> newHT;newHT._tables.resize(newSize);//遍历旧表,插入newHTfor (auto& e : _tables){if (e._state == EXITS){newHT.Insert(e._kv);}}newHT._tables.swap(_tables);}HashFunc hf;size_t starti = hf(kv.first);//调用仿函数,获取整数starti %= _tables.size();//求模取余 -- 但是不能除0size_t hashi = starti;size_t i = 1;//线性探测/二次探测while (_tables[hashi]._state == EXITS){hashi = starti + i;++i;hashi %= _tables.size();}_tables[hashi]._kv = kv;_tables[hashi]._state = EXITS;_n++;//有效数据个数++return true;}Data* Find(const K& key){//空表直接返回空指针if (_tables.size() == 0){return nullptr;}HashFunc hf;size_t starti = hf(key);starti %= _tables.size();size_t hashi = starti;size_t i = 1;while (_tables[hashi]._state != EMPTY){if (_tables[hashi]._state != DELETE && _tables[hashi]._kv.first == key){return &_tables[hashi];}hashi = starti + i;i++;hashi %= _tables.size();}return nullptr;}bool Erase(const K& key){Data* ret = Find(key);if (ret){ret->_state = DELETE;_n--;return true;}else{return false;}}private:vector<Data> _tables;size_t _n = 0; //存储关键字个数};
}
扩容时我们不能直接将原来的数据拷贝过去:
- 因为哈希是映射的关系,关键码值是通过数据和表的大小计算出来的
- 如果直接拷贝的话全都乱套了
- 这时我们需要重新映射

- 如图所示,也不是特别麻烦
- 直接建立一个新表,然后遍历旧表一次映射到新表中
- 不过扩容时会有不少的消耗
补充:
- 映射的时候取模
- 应该是对表的size()取模,而不是capacity()
- 因为对capacity取模的话,可能取到超出size的位置
- operator[]会对超出size的检查(不过有的也不检查,根据不同版本的库里定)
3.5 开散列 — 哈希桶、拉链法,开链法:
开散列: 开散列法又叫链地址法(哈希桶),首先对关键码集合用散列函数计算散列地址,具有相同地址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接来,各链表的头结点存储在哈希表中。

从上图可以看出,开散列中每个桶中放的都是发生哈希冲突的元素。
很显然,哈希桶中每个元素是个地址,所以哈希桶的底层原理就是一个指针数组,每个结点再挂着一个单链表,这样冲突就很容易解决了。
namespace Bucket
{template<class K, class V>struct HashNode{pair<K, V> _kv;HashNode<K, V>* _next;HashNode(const pair<K, V>& kv):_kv(kv), _next(nullptr){}};template<class K, class V, class HashFunc = DefaultHash<K>>class HashTable{typedef HashNode<K, V> Node;public:~HashTable(){for (size_t i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while (cur){Node* next = cur->_next;delete cur;cur = next;}_tables[i] = nullptr;}}bool Insert(const pair<K, V>& kv){if (Find(kv.first)){return false;}//新方法:(转移结点)//*原来单链表中的结点得到了利用,就不用去开新的结点了//负载因子 == 1 扩容HashFunc hf;if (_tables.size() == _n){size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;vector<Node*> newTable;newTable.resize(newSize, nullptr);for (size_t i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while (cur){Node* next = cur->_next;size_t hashi = hf(cur->_kv.first) % newSize;cur->_next = newTable[hashi];newTable[hashi] = cur;cur = next;}_tables[i] = nullptr;}newTable.swap(_tables);}size_t hashi = hf(kv.first);hashi %= _tables.size();//头插到对应的桶即可(单链表的尾插效率不高,但是头插效率高)Node* newnode = new Node(kv);newnode->_next = _tables[hashi];_tables[hashi] = newnode;_n++;return true;}//定位到桶,然后在同中挨个找一遍Node* Find(const K& key){if (_tables.size() == 0){return nullptr;}HashFunc hf;size_t hashi = hf(key);//size_t hashi = HashFunc()(key);hashi %= _tables.size();Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key){return cur;}cur = cur->_next;}return nullptr;}bool Erase(const K& key){if (_tables.size() == 0){return false;}HashFunc hf;size_t hashi = hf(key);hashi %= _tables.size();Node* prev = nullptr;Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key){if (prev == nullptr){_tables[hashi] = cur->_next;}else{prev->_next = cur->_next;}delete cur;return true;}prev = cur;cur = cur->_next;}return false;}private://指针数组vector<Node*> _tables;size_t _n = 0;};
}
扩容我们有两种方案:
方案一:

方案二:

很显然我们更倾向于方案二:
- 以为方案二中是将原来单链表中的结点得到了利用,就不用去开新的结点了
- 而方案一则是又开了一遍新的结点,效率不高
- 方案一是拷贝创建新的结点,方案二是转移结点
哈希表的析构:

虽然vector自己的析构函数可以释放哈希表,但是哈希桶中挂着的每个结点是不能释放的,需要我们手动释放掉。
相关文章:

【C++、数据结构】哈希 — 闭散列与哈希桶的模拟实现
文章目录📖 前言1. STL中哈希表的两个应用⚡1.1 🌟unordered_set1.2 🌟unordered_map2. 常见查找的性能对比💥3. 哈希表模拟实现🏁3.1 哈希的概念:3.2 哈希函数:3.3 哈希冲突:3.4 闭…...
vue 开发环境 卸载node 版本 切换新的 node 版本 mac电脑
注意:操作的机器当前是mac,先卸载,再安装 1.查看现有 node 版本 node -v2.卸载现有 node 版本, 1.卸载从node官网下载pkg安装的node sudo rm -rf /usr/local/{bin/{node,npm},lib/node_modules/npm,lib/node,share/man/*/node…...
在Linux和Windows上安装Nacos-2.1.1
记录:377场景:在CentOS 7.9操作系统安装Nacos-2.1.1。在Windows操作系统上安装Nacos-2.1.1。Nacos:Nacos: Dynamic Naming and Configuration Service。Nacos提供动态配置服务、服务发现及管理、动态DNS服务功能。版本:JDK 1.8 Na…...
解决QML debugging is enabled.Only use this in a safe environment.警告
系列文章目录 文章目录系列文章目录前言一、警告原因二、解决办法参考前言 我试图运行一个非常简单的程序,当单击退出按钮时关闭窗口,但获取以下输出,前提是包含按钮的应用程序窗口不显示: 您已启用QML调试(实际上它默认启用)&…...
)
华为OD机试真题JAVA实现【N进制减法】真题+解题思路+代码(20222023)
🔥系列专栏 华为OD机试(JAVA)真题目录汇总华为OD机试(Python)真题目录汇总华为OD机试(C++)真题目录汇总华为OD机试(JavaScript)真题目录汇总文章目录 🔥系列专栏题目输入输出描述示例一输入输出说明解题思路Code代码运行结果版权说明<...

ACM第一周---周训---题目合集.
🚀write in front🚀 📝个人主页:认真写博客的夏目浅石.CSDN 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 📣系列专栏:ACM周训练题目合集.CSDN 💬总结:…...

SCI学术论文的基本架构,以及Results、Discussion、Conclusion这三者的区别
SCI论文七大部分,各自应包含哪些内容 SCI写作——论文的结构 一篇SCI论文的大致框架包括Title, Abstract, Introduction, Methods/Methodology, Results, Discussion, Conclusion。不同的学科会有细微的变化,但大体框架基本不变。 1、标题Title 标题用…...

二叉树性质
在二叉树的第i层上至多有2^(i-1)个结点(i≥1)深度为k的二叉树至多有2^k-1个结点(k≥1)对任何一颗二叉树T,如果其叶子数为n0,度为2的结点数位n2,则n0n21满二叉树ÿ…...

二维数组操作示例
给定一个二维字符串数组,求对其按每个一维数组升序排列并按矩阵输出 //创建 String[][] twoDimension {{"A1","A2","A3"},{"B1","B2","B3"}}; List<String> arrayToList null; List<St…...
Spring Boot邮件发送(powernode CD2207)(内含教训视频+源代码)
Spring Boot邮件发送(powernode CD2207)(内含教训视频源代码) 教学视频源代码下载链接地址:https://download.csdn.net/download/weixin_46411355/87452056 目录Spring Boot邮件发送(powernode CD2207&…...

FortiTalk | “三英论安全”之OT安全热门话题解读
OT安全热门话题解读 在数字化转型时代,OT/IT融合已经成为主旋律,可能很多人还没有意识到“工厂”已经不是以前的“工厂”。从封闭走向互联、从现场走向远程、从手动走向自动,这种变革带来的不仅是便捷和效率,更潜藏着巨大的网络安…...
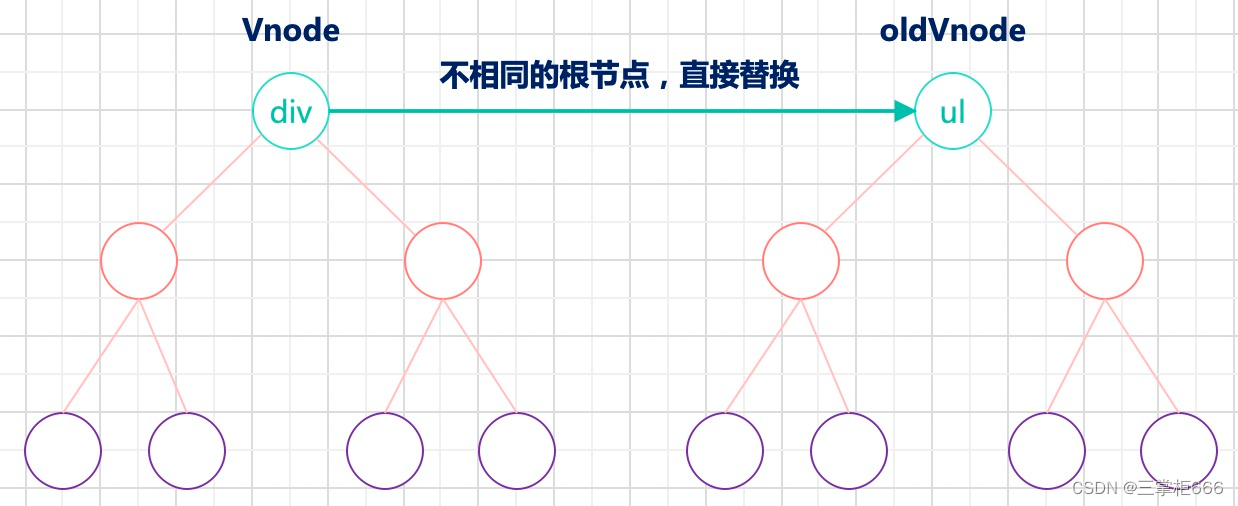
前端开发:关于diff算法详解
前言 前端开发中,关于JS原生的内容和前端算法相关的内容一直都是前端工作中的核心,不管是在实际的前端业务开发还是前端求职面试,都是非常重要且必备的内容。那么本篇博文来分享一个关于前端开发中必备内容:diff算法,d…...
如何为报表开发工具 FastReport .NET 设置 Apache 2 Web 服务器?
FastReport .NET是一款全功能的Windows Forms、ASP.NET和MVC报表分析解决方案,使用FastReport .NET可以创建独立于应用程序的.NET报表,同时FastReport .Net支持中文、英语等14种语言,可以让你的产品保证真正的国际性。专业版和企业版包括Fast…...
)
华为OD机试真题JAVA实现【出租车计费】真题+解题思路+代码(20222023)
🔥系列专栏 华为OD机试(JAVA)真题目录汇总华为OD机试(Python)真题目录汇总华为OD机试(C++)真题目录汇总华为OD机试(JavaScript)真题目录汇总文章目录 🔥系列专栏题目输入输出示例一输入输出说明示例二输入输出说明...

MySQL 查看版本的 5 种方法
MySQL 提供了几种用于查看服务器版本的方法,本文给大家做个简单的介绍。 方法一:登录 MySQL 每次通过 mysql 客户端连接服务器之后,都会显示一个欢迎信息,里面包含了服务器的版本: mysql -uroot Enter password: **…...
【软件测试】稳定性测试怎么做,这篇文章彻底讲透了~
稳定性对产品的重要性不言而喻。 而作为质量保障,在稳定性测试方面的探索也在不断演化。记得两年前我们做稳定性测试还是基于恒定的压力,7*24小时长时间运行,关注的指标无非是吞吐量TPS的抖动、响应时间的变化趋势,以及各种资源是…...
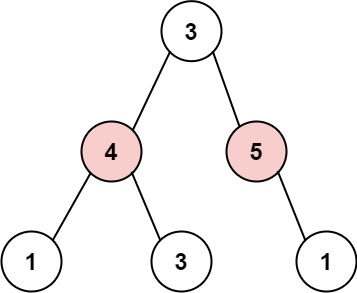
Leetcode:198. 打家劫舍、213. 打家劫舍 II、337. 打家劫舍 III(C++)
目录 198. 打家劫舍 问题描述: 实现代码与解析: 动态规划(版本一): 原理思路: 动态规划(版本二): 原理思路: 213. 打家劫舍 II 问题描述:…...

【每日随笔】手指训练 ( 手指训练作用 | 哪些人需要手指训练 | 手指操 | 手指康复训练器材 )
文章目录一、手指训练作用二、哪些人需要手指训练三、手指操四、手指康复训练器材产品需求探索 , 研究下手指训练的市场 , 前景 , 是否可以开发 ; 一、手指训练作用 手指训练作用 : 改善 上肢协调性手眼 协调性训练提高 手指 抓握 能力提高 手指 灵活性提高 上肢运动 准确性 和…...

ATR指标在外汇交易中的另类运用方法
当涉及到外汇交易时,有许多不同的指标可以使用。然而,ATR指标可能是一个被低估的工具,可以帮助您发现有利可图的交易机会。本文将介绍ATR指标是什么,如何使用它来识别价格波动和制定交易策略,以及如何在外汇市场中另辟…...

SQL Server 数据批量导出处理
在实际项目环境中,有时会遇到需要将大量数据(这里所指百万级别以上的数据量)从一台服务器迁移到另外一台数据库服务器的情况。SQL Server有很多方式可以进行数据迁移:备份还原、导入/导出数据、生成脚本(包含数据&…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
