PID控制算法进阶
关于PID控制算法基础概念在本文不再重复了,详情可参考:PID控制算法基础介绍
本文主要从PID算法代码实现,代码解析,理论进阶,PID调参等方向进行阐述。
目录
- 位置式PID和增量式PID
- 1.1 位置式PID
- 1.2 增量式PID
- 1.3 位置式和增量式PID区别
- 积分限幅
- 位置式PID参数调试
- 代码实现
位置式PID和增量式PID
1.1 位置式PID
(1)基本的连续PID控制
公式:
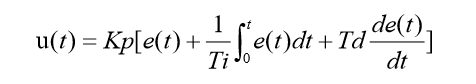
(2)离散PID控制
将连续的进行离散化。
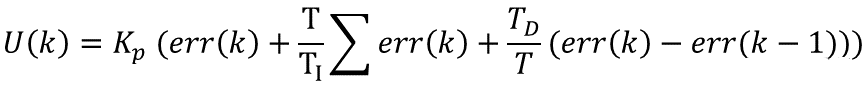
展开简化一下就是:
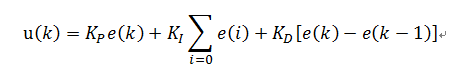
e(k): 用户设定的值(目标值) - 控制对象的当前的状态值
比例P : e(k)
积分I : ∑e(i) 误差的累加
微分D : e(k) - e(k-1) 这次误差-上次误差
也就是位置式PID是当前系统的实际位置,与你想要达到的预期位置的偏差,进行PID控制
因为有误差积分 ∑e(i),一直累加,也就是当前的输出u(k)与过去的所有状态都有关系,用到了误差的累加值;(误差e会有误差累加),输出的u(k)对应的是执行机构的实际位置,一旦控制输出出错(控制对象的当前的状态值出现问题 ),u(k)的大幅变化会引起系统的大幅变化
并且位置式PID在积分项达到饱和时,误差仍然会在积分作用下继续累积,一旦误差开始反向变化,系统需要一定时间从饱和区退出,所以在u(k)达到最大和最小时,要停止积分作用,并且要有积分限幅和输出限幅
所以在使用位置式PID时,一般我们直接使用PD控制
而位置式 PID 适用于执行机构不带积分部件的对象,如舵机、平衡小车的直立、温控系统的控制
1.2 增量式PID
(1)公式推导过程
(a)k-1时刻的离散表示:
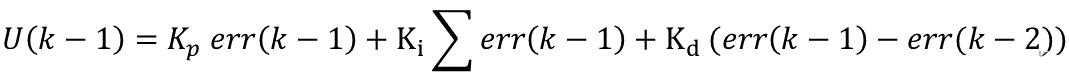 (b)利用deltUk = U(k) - U(K-1),得到本次的增量:
(b)利用deltUk = U(k) - U(K-1),得到本次的增量:
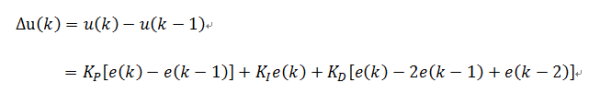
比例P : e(k)-e(k-1) 本次误差-上次误差
积分I : e(k) 本次误差
微分D : e(k) - 2e(k-1)+e(k-2) 本次误差-2*上次误差+上上次误差
增量式PID根据公式可以很好地看出,一旦确定了 KP、TI 、TD,只要使用前后三次测量值的偏差, 即可由公式求出控制增量
而得出的控制量Δu(k)对应的是近几次位置误差的增量,而不是对应与实际位置的偏差。 没有误差累加
也就是说,增量式PID中不需要累加。控制增量Δu(k)的确定仅与最近3次的采样值有关,容易通过加权处理获得比较好的控制效果,并且在系统发生问题时,增量式不会严重影响系统的工作。
1.3 位置式和增量式PID区别
1、增量式算法不需要做累加,控制量增量的确定仅与最近几次偏差采样值有关,计算误差对控制 量计算的影响较小。而位置式算法要用到过去偏差的累加值,容易产生较大的累加误差。
2、增量式算法得出的是控制量的增量,例如在阀门控制中,只输出阀门开度的变化部分,误动作 影响小,必要时还可通过逻辑判断限制或禁止本次输出,不会严重影响系统的工作。 而位置式的输出直接对应对象的输出,因此对系统影响较大。
3、增量式PID控制输出的是控制量增量,并无积分作用,因此该方法适用于执行机构带积分部件的对象,如步进电机等,而位置式PID适用于执行机构不带积分部件的对象,如电液伺服阀。
4、在进行PID控制时,位置式PID需要有积分限幅和输出限幅,而增量式PID只需输出限幅
积分限幅
积分限幅实际比较多,所以也提一下。
(1)针对问题:
在开始控制后,有一个较大误差,且有一个非常大干扰的话,例如外界阻力,阻止其误差减小,如旋翼飞机被人死死的按住。虽然他的PI都在输出,但是误差一直没变。这时候,随着时间的拉长,积分的输出值会越来越大。
这将导致以下问题:
a)这种输出可能超过了控制系统承受范围
b)而一旦这种阻力去掉,会使得这种输出很大很大,引起很大的超调和震荡。
(2)解决方法
引入积分限幅。原理给定一个积分输出的最大值限制,一旦超出,则不再增加。
位置式PID参数调试
PID调节的具体过程一般有理论计算整定法和工程整定法。对于复杂的、非线性的系统通常用工程整定法,即根据工程经验试凑出合理的参数。PID参数的设置步骤一般如下:
(1)首先选择一个合适的并且尽量短的采样时间让系统工作;
(2)首先加入比例环节,调节比例系数,直到系统的输出出现临界振荡;
(3)若单独的比例环节不能满足设计要求,则此时加入积分环节,调整好的比例系数缩小为原来的0.8,然后调节积分时间参数,使得系统能保持较小的稳态误差和较小的振荡时间,此时可以同时调整比例系数和积分时间常数,直到得到较为满意的结果;
(4)如若还不是特别满意,可以增加微分环节,从小到大逐渐增加微分时间常数,同时相应的更改比例系数和积分时间,试凑出合适参数。
实际使用时,PID可能不是都使用的,有:
(1)PI,D=0
有自然的阻尼的情况。如水中弹簧震荡,水有阻尼,或者阻尼能够较好的平衡掉该中情况下PI的震荡。
(2)PD,I=0
没有外界阻力情况,物理机械能够保证自平衡。
比如在水平面上小车控制运动到指定位置,且这个小车电机等没有阻力,到位置后不需要再输出就可以保持。
调整PID参数对系统的影响:
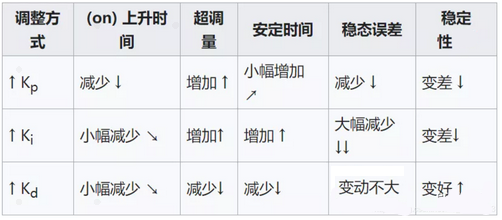
PID参数调整口诀:
参数整定找最佳,从小到大顺序查,
先是比例后积分,最后再把微分加,
曲线振荡很频繁,比例度盘要放大,
曲线漂浮绕大弯,比例度盘往小扳,
曲线偏离回复慢,积分时间往下降,
曲线波动周期长,积分时间再加长,
曲线振荡频率快,先把微分降下来,
动差大来波动慢,微分时间应加长,
理想曲线两个波,前高后低四比一,
一看二调多分析,调节质量不会低
注:比例度盘,kp倒数
积分时间,Ti倒数
微分时间,Td
代码实现
typedef struct PID
{ float P,I,D,limit;
}PID;typedef struct Error
{float Current_Error;//当前误差float Last_Error;//上一次误差float Previous_Error;//上上次误差
}Error;/*! * @brief 位置式PID* *sptr :误差参数* *pid: PID参数* NowPlace:当前位置* Point: 目标位置 */// 位置式PID控制
float PID_Realize(Error *sptr,PID *pid, int32 NowPlace, float Point)
{int32 iError, // 当前误差Realize; //实际输出 iError = Point - NowPlace; // 计算当前误差sptr->Current_Error += pid->I * iError; // 误差积分sptr->Current_Error = sptr->Current_Error > pid->limit?pid->limit:sptr->Current_Error;//积分限幅sptr->Current_Error = sptr->Current_Error <-pid->limit?-pid->limit:sptr->Current_Error;Realize = pid->P * iError //比例P+ sptr->Current_Error //积分I+ pid->D * (iError - sptr->Last_Error); //微分Dsptr->Last_Error = iError; // 更新上次误差return Realize; // 返回输出值
}/*! * @brief 增量式PID* *sptr :误差参数* *pid: PID参数* NowPlace:实际值* Point: 期望值*/
// 增量式PID控制
int32 PID_Increase(Error *sptr, PID *pid, int32 NowPlace, int32 Point)
{int32 iError, //当前误差Increase; //最后得出的实际增量iError = Point - NowPlace; // 计算当前误差Increase = pid->P * (iError - sptr->Last_Error) //比例P+ pid->I * iError //积分I+ pid->D * (iError - 2 * sptr->Last_Error + sptr->Previous_Error); //微分Dsptr->Previous_Error = sptr->Last_Error; // 更新前次误差sptr->Last_Error = iError; // 更新上次误差return Increase; // 返回增量
}
实际使用时,需要定时周期性采集数据进行PID计算,需要根据场景决定合适的采样周期。
上面那套比较简单方便理解,下面这套比较完善,更实用,都可参考:
#define LimitMax(input, max) \{ \if (input > max) \{ \input = max; \} \else if (input < -max) \{ \input = -max; \} \}enum PID_MODE
{PID_POSITION = 0,PID_DELTA
};typedef struct
{//PID运算模式uint8_t mode;//PID 三个基本参数float Kp;float Ki;float Kd;float max_out; //PID最大输出 (输出限幅)float max_iout; //PID最大积分输出 (积分限幅)float set; //PID目标值float fdb; //PID当前值float out; //三项叠加输出float Pout; //比例项输出float Iout; //积分项输出float Dout; //微分项输出//微分项最近三个值 0最新 1上一次 2上上次float Dbuf[3]; //误差项最近三个值 0最新 1上一次 2上上次float error[3];
} pid_type_def;void PID_init(pid_type_def *pid, uint8_t mode, const float PID[3], float max_out, float max_iout)
{if (pid == NULL || PID == NULL){return;}pid->mode = mode;pid->Kp = PID[0];pid->Ki = PID[1];pid->Kd = PID[2];pid->max_out = max_out;pid->max_iout = max_iout;pid->Dbuf[0] = pid->Dbuf[1] = pid->Dbuf[2] = 0.0f;pid->error[0] = pid->error[1] = pid->error[2] = pid->Pout = pid->Iout = pid->Dout = pid->out = 0.0f;
}void PID_clear(pid_type_def *pid)
{if (pid == NULL){return;}//当前误差清零pid->error[0] = pid->error[1] = pid->error[2] = 0.0f;//微分项清零pid->Dbuf[0] = pid->Dbuf[1] = pid->Dbuf[2] = 0.0f;//输出清零pid->out = pid->Pout = pid->Iout = pid->Dout = 0.0f;//目标值和当前值清零pid->fdb = pid->set = 0.0f;
}float PID_calc(pid_type_def *pid, float ref, float set)
{//判断传入的PID指针不为空if (pid == NULL){return 0.0f;}//存放过去两次计算的误差值pid->error[2] = pid->error[1];pid->error[1] = pid->error[0];//设定目标值和当前值到结构体成员pid->set = set;pid->fdb = ref;//计算最新的误差值pid->error[0] = set - ref;//判断PID设置的模式if (pid->mode == PID_POSITION)//位置式PID{//比例项计算输出pid->Pout = pid->Kp * pid->error[0];//积分项计算输出pid->Iout += pid->Ki * pid->error[0];//存放过去两次计算的微分误差值pid->Dbuf[2] = pid->Dbuf[1];pid->Dbuf[1] = pid->Dbuf[0];//当前误差的微分用本次误差减去上一次误差来计算pid->Dbuf[0] = (pid->error[0] - pid->error[1]);//微分项输出pid->Dout = pid->Kd * pid->Dbuf[0];//对积分项进行限幅LimitMax(pid->Iout, pid->max_iout);//叠加三个输出到总输出pid->out = pid->Pout + pid->Iout + pid->Dout;//对总输出进行限幅LimitMax(pid->out, pid->max_out);}else if (pid->mode == PID_DELTA)//增量式PID{//以本次误差与上次误差的差值作为比例项的输入带入计算pid->Pout = pid->Kp * (pid->error[0] - pid->error[1]);//以本次误差作为积分项带入计算pid->Iout = pid->Ki * pid->error[0];//迭代微分项的数组pid->Dbuf[2] = pid->Dbuf[1];pid->Dbuf[1] = pid->Dbuf[0];//以本次误差与上次误差的差值减去上次误差与上上次误差的差值作为微分项的输入带入计算pid->Dbuf[0] = (pid->error[0] - 2.0f * pid->error[1] + pid->error[2]);pid->Dout = pid->Kd * pid->Dbuf[0];//叠加三个项的输出作为总输出 注意这里的符号是+=pid->out += pid->Pout + pid->Iout + pid->Dout;//对总输出限幅LimitMax(pid->out, pid->max_out);}return pid->out;
}
参考和推荐:
https://blog.csdn.net/kevinshift/article/details/124753170
https://blog.csdn.net/as480133937/article/details/89508034
https://zhuanlan.zhihu.com/p/85020348?utm_source=qq
https://zhuanlan.zhihu.com/p/84767869
https://blog.csdn.net/kevinshift/article/details/124753170
相关文章:

PID控制算法进阶
关于PID控制算法基础概念在本文不再重复了,详情可参考:PID控制算法基础介绍 本文主要从PID算法代码实现,代码解析,理论进阶,PID调参等方向进行阐述。 目录位置式PID和增量式PID1.1 位置式PID1.2 增量式PID1.3 位置式和…...

嵌入式工程师有什么值得一看的网站和书籍吗?
原文直达: 嵌入式工程师有什么值得一看的网站和书籍吗? - CodeAllen的回答 - 知乎 https://www.zhihu.com/question/68423119/answer/2885623392 我是资深网站保存爱好者,浏览器分门别类存了应该有几百个网址,关于嵌入式的也有很…...

操作系统的四个特征
一、并发 并发:是指两个或多个事件在同一时间间隔内发生。这些事件宏观上是同时发生的,但微观上是交替发生的。 并行:指两个或多个事件在同一时刻同时发生。 操作系统的并发性指计算机系统中同时存在着多个运行的程序。操作系统和程序并发…...
Django框架之模型shell工具和查看MySQL数据库日志
shell工具和查看MySQL数据库日志 1 shell工具 Django的manage工具提供了shell命令,帮助我们配置好当前工程的运行环境(如连接好数据库等),以便可以直接在终端中执行测试python语句。 通过如下命令进入shell python manage.py …...
电脑录屏怎样不录到外界声音?调整这一个开关,即可实现
有很多小伙伴希望自己电脑录屏的时候,不要录制自己的声音,而是通过后期配音的方式完成视频创作。电脑录屏怎样不录到外界声音?其实只需要调整这一个开关,就能实现不录外界声音,一起来看看吧。 不录外界声音1…...

无需登录复制网站文字的解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。喜欢通过博客创作的方式对所学的知识进行总结与归纳,不仅形成深入且独到的理…...
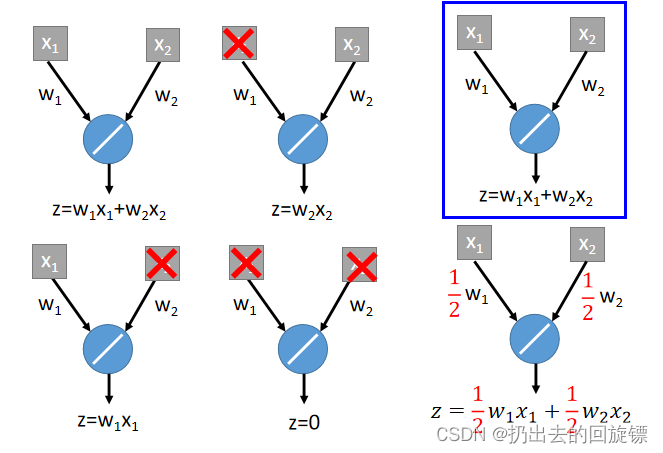
ccc-Tips for Deep Learning-李宏毅(8)
文章目录Recipe of Deep LearningGood Results on Training DataNew activation functionAdaptive Learning RateGood Results on Testing DataEarly StoppingRegularizationDropoutwhy Dropout work?Reason for bias&varianceDropout is a kind of ensembleRec…...

ArkUI新能力,助力应用开发更便捷
ArkUI是一套构建分布式应用的声明式UI开发框架。它具备简洁自然的UI信息语法、丰富的UI组件、多维的状态管理,以及实时界面预览等相关能力,帮助您提升应用开发效率,并能在多种设备上实现生动而流畅的用户体验。随着HarmonyOS 3.1版本的发布&a…...

vue面试题大全
Vue面试题大全一.vue的基本原理二.双向数据绑定的原理三.使用object.defineProperty()来进行数据劫持有什么缺点?一.vue的基本原理 当一个vue实例创建的时候,vue会遍历data中的属性,用object.defineProperty,将它们转为getter/se…...
P1307 [NOIP2011 普及组] 数字反转
[NOIP2011 普及组] 数字反转 题目描述 给定一个整数 NNN,请将该数各个位上数字反转得到一个新数。新数也应满足整数的常见形式,即除非给定的原数为零,否则反转后得到的新数的最高位数字不应为零(参见样例 2)。 输入…...
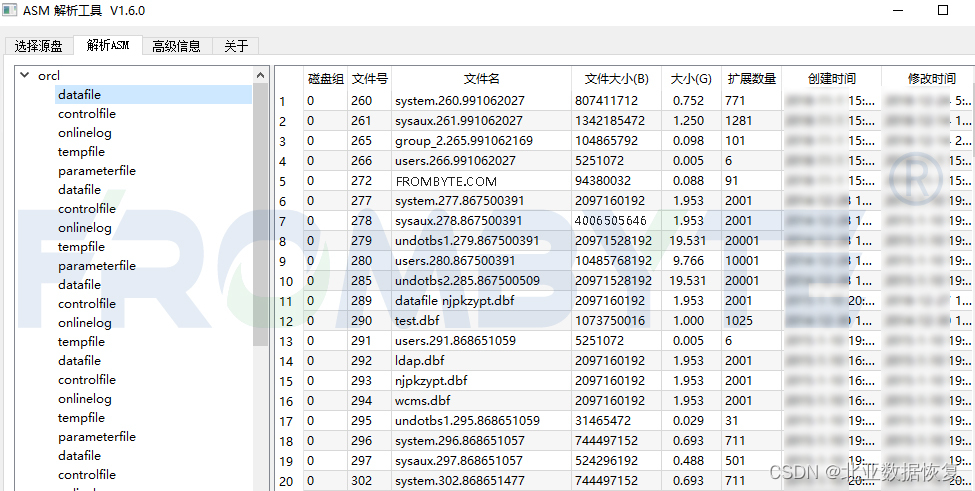
【服务器数据恢复】NetApp存储无法访问的数据恢复案例
服务器数据恢复环境: NetApp某型号存储; 配备SAS硬盘,该硬盘520字节一个扇区; 所有的lun映射到小型机使用,存放Oracle数据库文件,采用ASM裸设备存储方式。 服务器故障: 管理员误操作删除NetApp…...
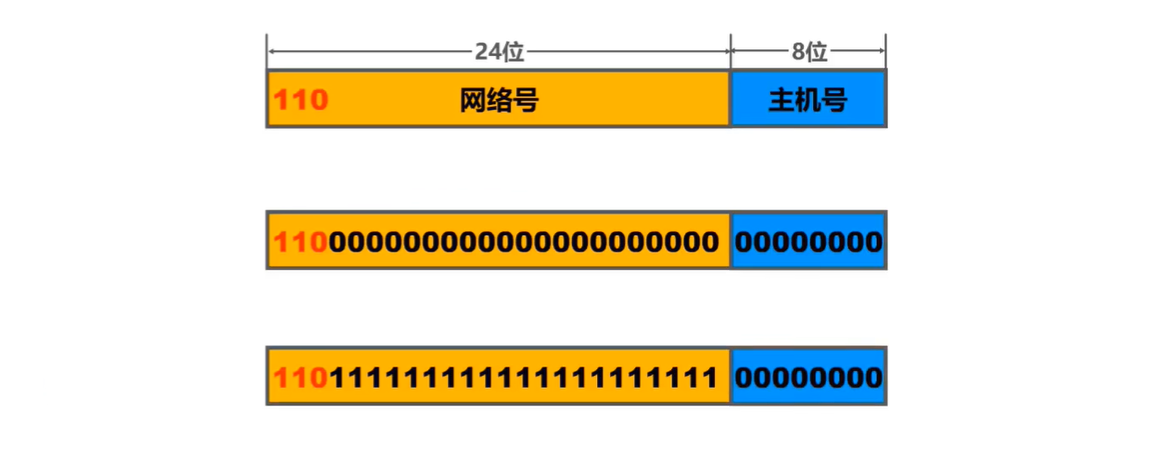
(考研湖科大教书匠计算机网络)第四章网络层-第三节2:分类编址的IPv4地址
获取pdf:密码7281专栏目录首页:【专栏必读】考研湖科大教书匠计算机网络笔记导航 文章目录一:分类IP地址概述二:各类地址详解(1)A类地址(2)B类地址(3)C类地址…...
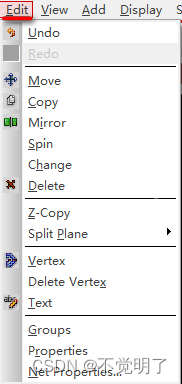
Allegro移动器件时附带的孔和线被同步更改的原因和解决办法
Allegro移动器件时附带的孔和线被同步更改的原因和解决办法 用Allegro做PCB设计的时候,移动器件的时候,会出现附带的孔和线也会被同步更改,有时并不是期望的效果,如下图 Allegro其实将这个功能关闭即可,具体操作如下 选择Edit点击Move命令...

工程监测多通道振弦模拟信号采集仪VTN参数修改
工程监测多通道振弦模拟信号采集仪VTN参数修改 1 使用按键修改参数 使用按键修改某个参数的方法如下: (1)在系统参数查看页面(PXX 页面),按【SWITCH】或【SETTING】按键切换到要修改的参数项。 (…...

【算法】差分
作者:指针不指南吗 专栏:算法篇 🐾合理规划时间与精力🐾 1.什么是差分? 与前缀和是反函数 原数组a a1 , a2 , a3 , a4 , a5 , a6 , a7 构造数组b a1b1; a2b1b2; a3b1b2b3; … aib1b2b3…bi; 构造一个b数组使得&#…...
【LeetCode】剑指 Offer(1)
目录 写在前面: 题目1:剑指 Offer 03. 数组中重复的数字 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 题目2:剑指 Offer 06. 从…...
linux rancher 清理docker容器磁盘空间
目录说明 /var/lib/docker/containers: 是 Docker 在 Linux 系统上默认存储容器信息的目录。在该目录下,每个运行的 Docker 容器都有一个单独的目录,以容器 ID 命名,其中包含有关该容器的元数据和日志文件。 具体来说࿰…...

移动端兼容性问题集锦
前言 去年主要工作就是混合开发,写app内嵌的h5。在开发期间多多少少遇到些兼容性问题,最近工作比较清闲,整理下方便以后查阅,也希望能帮助到一些同学。 并且本文会持续补充内容,欢迎关注我,另外我会更新一…...

【Spark分布式内存计算框架——Spark SQL】4. DataFrame(上)
3.1 DataFrame是什么 在Spark中,DataFrame是一种以RDD为基础的分布式数据集,类似于传统数据库中的二维表格。DataFrame与RDD的主要区别在于,前者带有schema元信息,即DataFrame所表示的二维表数据集的每一列都带有名称和类型。 使…...
GPS通信
目录 一、GPS启动的方式 二、GPS经纬度坐标转换 三、GPS定位和网络定位 四、3D定位和2D 定位 五、同步GPS时间到本地时间 六、卫星分布对GPS performance有很大影响吗 一、GPS启动的方式 热启动:指在上次关机的地方没有过多移动过,且距离上次定位…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...
