下一个排列-力扣31-java
一、题目描述
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
例如,arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
例如,arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地,arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须 原地 修改,只允许使用额外常数空间。
示例 1:
输入:nums = [1,2,3]
输出:[1,3,2]
示例 2:
输入:nums = [3,2,1]
输出:[1,2,3]
示例 3:
输入:nums = [1,1,5]
输出:[1,5,1]
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/next-permutation
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
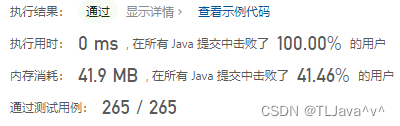
二、运行结果
三、解题思路
首先从后往前找到第一个减小的数字,记录其下标为index,如1357642,找到的数字是5,重点:该数字后面的所有数字是按从大到小排列的。如果不是,则表示在该数字之后还出现过减小的数字,那么当前数字就是不是倒序第一个减小的,矛盾。
如果没有找到减小的数字,就表示每一位数字都是按降序排列的,没有下一个更大的序列,逆置该数组返回即可。
如果找到了index,则从该下标往后找到比nums[index]大,而且是这数中最小的,如上面的数字找到的是6,然后交换5和6的位置,则数组变为1367542,index后面的数字仍是降序排列(7542),将index后面的所有数字变为升序排列(最小的排列)即可,此时数字变为1362457,即是下一个更大的排列。
四、AC代码
class Solution {public void nextPermutation(int[] nums) {int len = nums.length;int index = -1;for(int i=len-2; i>=0; i--){ //从后往前找到第一个下降的数字下标if(nums[i] < nums[i+1]){index = i;break;}}if(index == -1){ //不存在下一个更大的排列int i=0, j = len-1;while(i < j) { //重新排列成最小的排列swap(nums, i, j);i++; j--; }return ;}int i = index;//寻找后面比该数字大的最小数字下标while(i < len-1 && nums[i+1] > nums[index]) i++; swap(nums, i, index); //交换两个位置的元素int j=index+1, k = len-1;while(j < k){ //将该数字后面的数排成最小序列(逆置)swap(nums, j, k);j++; k--;}}private void swap(int[] nums, int i, int j){int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;}
}相关文章:

下一个排列-力扣31-java
一、题目描述整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。例如,arr [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地&…...

前端面试题
1.HTTP request报文结构是怎样的 1.首行是Request-Line包括:请求方法,请求URI,协议版本,CRLF(换行符) 2.首行之后是若干行请求头,包括general-header,request-header或者entity-hea…...
jsp游戏门户网站系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 jsp 游戏门户网站系统 是一套完善的web设计系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为 TOMCAT7.0,Myeclipse8.5开发,数据库为Mysql,使…...
Git与IDEA强强联合(HTTPS协议连接)
最近在写项目的时候,在台式机和笔记本之间频繁切换,竟然还是用qq传压缩包,我自己都感觉无语,有git这样强大的版本管理工具,我竟然没想起来。然后也没有相关的博文就想来更新一篇。 那么如何使idea和git强强联合呢&…...

leetcode 第二题:两数相加-C语言实现
题目地址 备注: 不要忘记最后一个进位的可能。可以使用typedef,来简化struct的书写 代码实现: #include<stdio.h> #include<stdlib.h>struct listNode {int val;struct listNode* next; };// 使用typedef typedef struct lis…...

【人工智能】PTP网络时钟服务器在智能驾驶里的重要性
【人工智能】PTP网络时钟服务器在智能驾驶里的重要性 【人工智能】PTP网络时钟服务器在智能驾驶里的重要性 一辆宣称具备L4/L5自动驾驶功能的车辆,如果多个激光雷达之间的时间同步不够精确?如果传感器感知数据通过以太网传输到智驾域控制器的延迟不可控…...
【蓝桥杯集训3】二分专题(3 / 5)
目录 二分模板 1460. 我在哪? - 二分答案 哈希表 1221. 四平方和 - 哈希表 / 二分 1、哈希表 2、二分 自定义排序 1227. 分巧克力 - 113. 特殊排序 - 二分模板 l r >> 1 —— 先 r mid 后 l mid1 —— 寻找左边界 —— 找大于某个数的最小值lr…...

在成都的哪个培训机构学习Java好呢?
自从小课06年进入成都这个IT培训市场以来,短短十几年,招过很多学员,也见证过很多机构的起起落落。心中有万分的感慨,总结下来有这几点分享给大家,在选择培训机构时能看清本质,找到适合自己靠谱的机构学Java…...
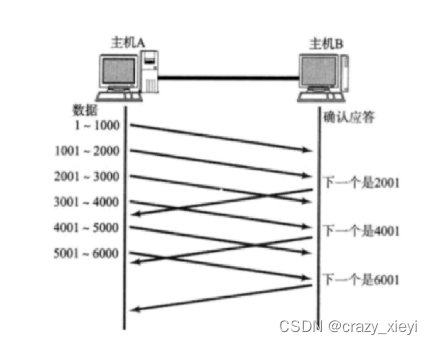
传输层重要协议之UDP协议和TCP协议详解
更多关于UDP协议和TCP协议请移步官网:https://www.rfc-editor.org/standards#ISUDP标准协议文档-RFC 768TCP标准协议文档-RFC 793UDP协议详解UDP协议的特点:无连接、不可靠传输、面向数据报和全双工。UDP协议报文结构:关于端口号:…...
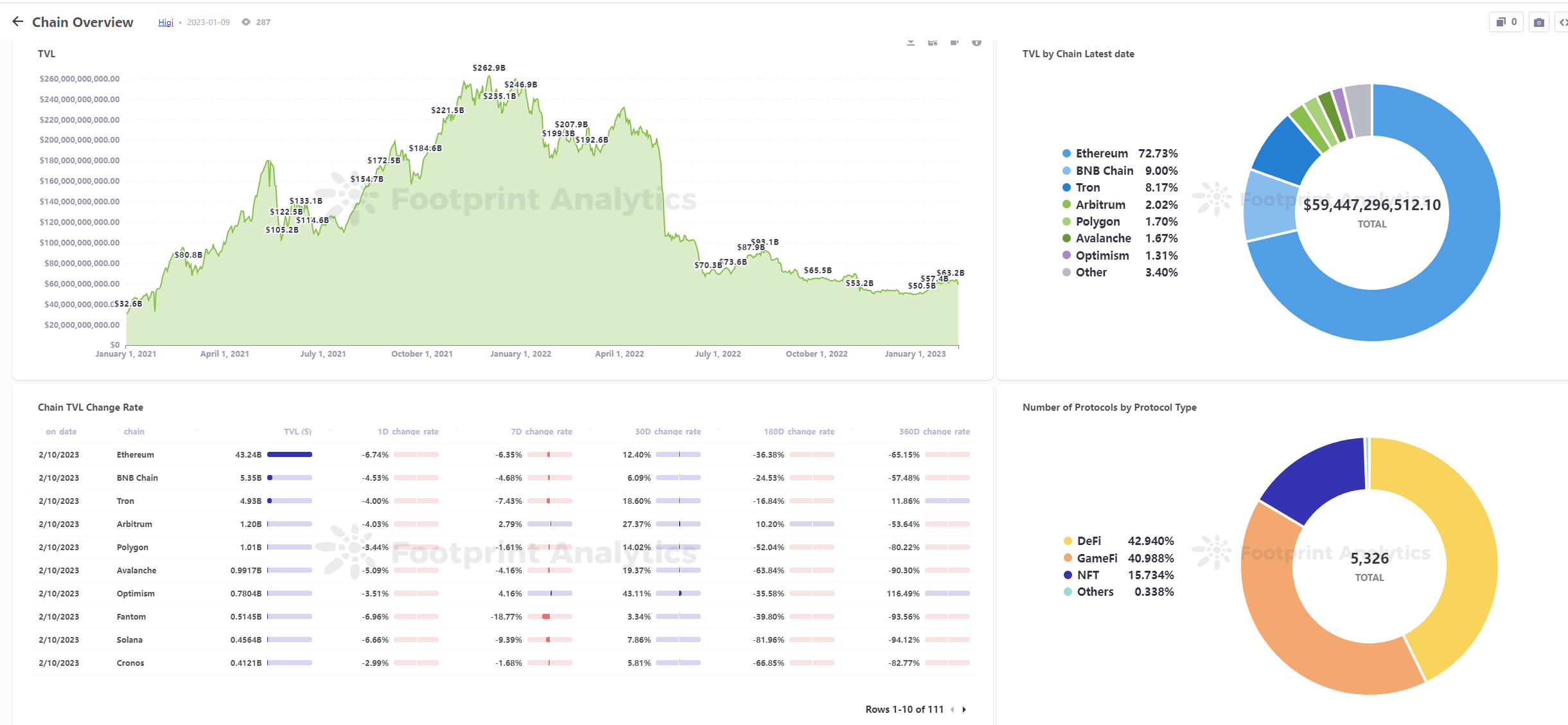
BNB Greenfield 成存储赛道“新贵”,BNB 生态的野心与破局
“从BNB Beacon Chain,到BNB Chain,再到BNB Greenfield ,三位一体的 BNB 生态格局正式形成。 ”在今年的2月1日,币安发布了分布式存储链BNB Greenfield,根据白皮书信息,它的特别之处在于其不仅具备基于SP&a…...
:时间类型操作(上):日、月、年、时、分、秒之差及时间间隔计算)
【SQL开发实战技巧】系列(十六):时间类型操作(上):日、月、年、时、分、秒之差及时间间隔计算
系列文章目录 【SQL开发实战技巧】系列(一):关于SQL不得不说的那些事 【SQL开发实战技巧】系列(二):简单单表查询 【SQL开发实战技巧】系列(三):SQL排序的那些事 【SQL开发实战技巧…...

JavaScript知识点总结
JavaScript 一、介绍: 1.JavaScript是一种专门在浏览器编译并执行的编程语言 2.JavaScript处理用户与浏览器之间请求问题 3.JavaScript采用【弱类型编程语言风格】对【面向对象思想】来进行实现的编程语言 二、弱类型编程语言风格 VS 强类型编程语言风格 …...

adb命令记录
一、获取系统版本 adb shell getprop ro.build.version.release 二、手机文件拉取到电脑 adb命令 : adb pull source_path dest_path 示例: adb pull /sdcard/Movies/app_layout.txt ./ 从手机拉取app_layout.txt文件到当前路径。 三、电脑文件推送…...
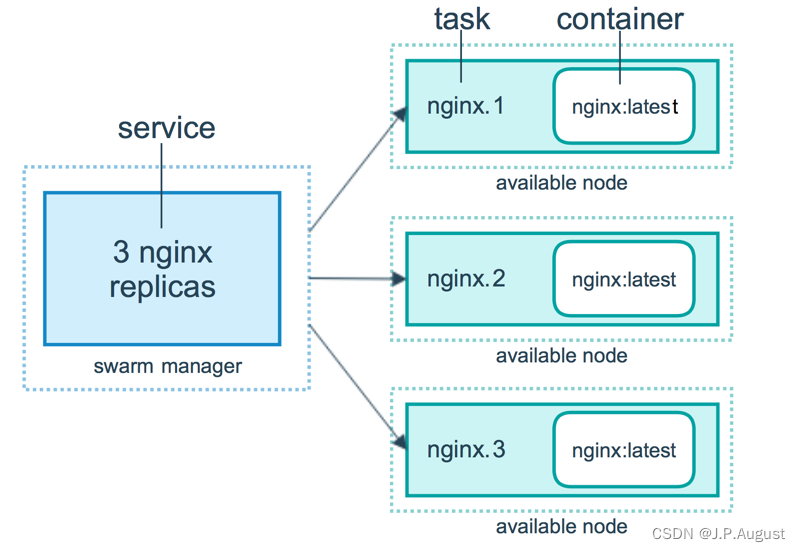
9.Docker Swarm
Docker Swarm 基本概念 Swarm是使用SwarmKit构建的 Docker 引擎内置(原生)的集群管理和编排工具。Docker Swarm是 Docker 官方三剑客项目之一,提供 Docker 容器集群服务,是 Docker 官方对容器云生态进行支持的核心方案。 使用它…...
基于tensorflow keras DNN神经网络训练预测豆瓣中文影评差评好评 附完整代码 +数据
首先看视频:https://www.bilibili.com/video/BV1r84y1p7q3/?spm_id_from=333.999.0.0 附完整的代码数据 完整的代码项目: 主要代码: # 导入包 import csv import jieba import tensorflow as tf from tensorflow...
商城系统必备营销工具(五)——积分商城
做商城,流量必不可少,日活跃度也很重要。现在各大APP、网站、小程序和微商城,基本都在为了巩固流量做积分商城,虽然已经随处可见,但很多企业商家却并没有将积分商城运作起来,积分商城也没有人浏览兑换商品。…...
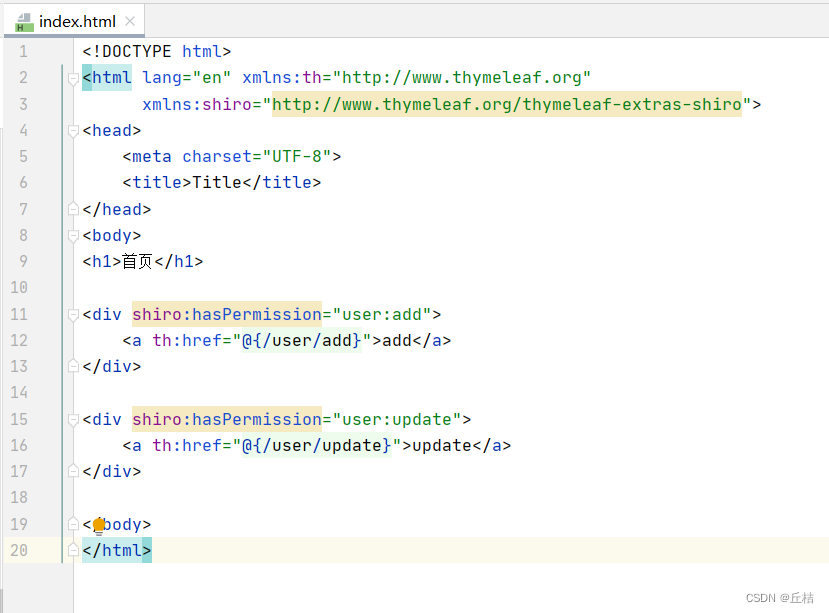
SpringBoot08:Shiro
什么是Shiro? 一个Java的安全(权限)框架,可以完成认证、授权、加密、会话管理、Web集成、缓存等 下载地址:Apache Shiro | Simple. Java. Security. 快速启动 先在官网找到入门案例:shiro/samples/quick…...

进击中的 Zebec 生态,Web2 与 Web3 世界的连接器
虽然从意识形态上看,Web2世界与Web3世界存在着不同的逻辑,但我们同样看到,随着加密资产领域的发展,其正在作为优质投资品,被以Paypal、高盛等主流机构重视与接受。当然,除了作为投资者品外,近年…...
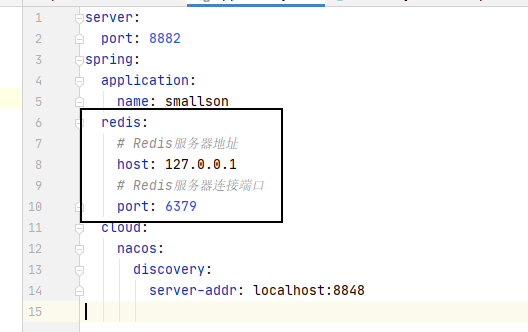
SpringCloud保姆级搭建教程五---Redis
首先,这个和微服务没有直接的关系,只是在代码开发当中要使用的一个工具而已,为了提高这个系统的性能,加快查询效率等方面而使用它1、首先,要先安装redis到电脑上,这里依然是在windows上演示,之后…...
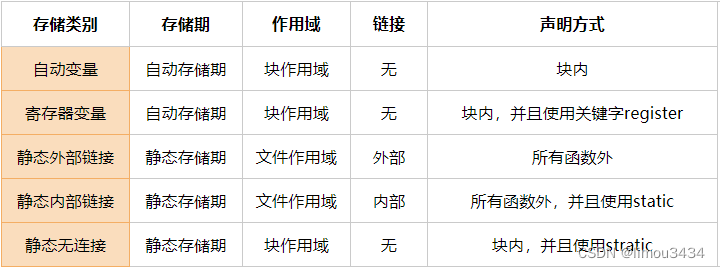
存储类别、链接与内存管理(一)
1、一些必要的基础概念 (1)对象 从硬件的角度,被存储的每个值都被占用了一定的物理内存,C语言把这样的一块内存称为对象对象可以存储一个或多个值一个对象可能并未存储实际的值,也可能存储一个或多个值,但…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...
