算法训练营 day48 动态规划 完全背包 零钱兑换 II 组合总和 Ⅳ
算法训练营 day48 动态规划 完全背包 零钱兑换 II 组合总和 Ⅳ
完全背包
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
在下面的讲解中,我依然举这个例子:
背包最大重量为4。
物品为:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
每件商品都有无限个!
01背包和完全背包唯一不同就是体现在遍历顺序上,所以本文就不去做动规五部曲了,我们直接针对遍历顺序经行分析!
我们知道01背包内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。
而完全背包的物品是可以添加多次的,所以要从小到大去遍历,即:
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}
dp状态图如下:

在完全背包中,对于一维dp数组来说,其实两个for循环嵌套顺序是无所谓的!
因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。
一维dp数组
//先遍历物品,再遍历背包
private static void testCompletePack(){int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagWeight = 4;int[] dp = new int[bagWeight + 1];for (int i = 0; i < weight.length; i++){ // 遍历物品for (int j = weight[i]; j <= bagWeight; j++){ // 遍历背包容量dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);}}for (int maxValue : dp){System.out.println(maxValue + " ");}
}
//先遍历背包,再遍历物品
private static void testCompletePackAnotherWay(){int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagWeight = 4;int[] dp = new int[bagWeight + 1];for (int i = 1; i <= bagWeight; i++){ // 遍历背包容量for (int j = 0; j < weight.length; j++){ // 遍历物品if (i - weight[j] >= 0){dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);}}}for (int maxValue : dp){System.out.println(maxValue + " ");}
}
二维dp数组
private static void testCompletePack(){int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagWeight = 4;int[][] dp = new int[weight.length][bagWeight + 1];for (int j = weight[0]; j <=bagWeight ; j++) {dp[0][j] = dp[0][j-weight[0]]+value[0];}for (int i = 1; i <weight.length ; i++) {for (int j = 1; j <=bagWeight ; j++) {if (j<weight[i]){dp[i][j] = dp[i-1][j];}else {dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);}}}for (int[] maxValue : dp){for (int a: maxValue) {System.out.print(a + " ");}System.out.println();}}
零钱兑换 II
518. 零钱兑换 II - 力扣(LeetCode)
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
本题和纯完全背包不一样,纯完全背包是凑成背包最大价值是多少,而本题是要求凑成总金额的物品组合个数!
组合不强调元素之间的顺序,排列强调元素之间的顺序。
-
确定dp数组以及下标的含义
dp[j]:凑成总金额j的货币组合数为dp[j]
-
确定递推公式
dp[j] 就是所有的dp[j - coins[i]](考虑coins[i]的情况)相加。
所以递推公式:dp[j] += dp[j - coins[i]];
-
dp数组如何初始化
dp[0]一定要为1,dp[0] = 1是 递归公式的基础。如果dp[0] = 0 的话,后面所有推导出来的值都是0了。
-
确定遍历顺序
因为纯完全背包求得装满背包的最大价值是多少,和凑成总和的元素有没有顺序没关系,即:有顺序也行,没有顺序也行!
而本题要求凑成总和的组合数,元素之间明确要求没有顺序。
所以纯完全背包是能凑成总和就行,不用管怎么凑的。
本题是求凑出来的方案个数,且每个方案个数是为组合数。
那么本题,两个for循环的先后顺序可就有说法了。
我们先来看 外层for循环遍历物品(钱币),内层for遍历背包(金钱总额)的情况。
代码如下:
for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量dp[j] += dp[j - coins[i]];} }假设:coins[0] = 1,coins[1] = 5。
那么就是先把1加入计算,然后再把5加入计算,得到的方法数量只有{1, 5}这种情况。而不会出现{5, 1}的情况。
所以这种遍历顺序中dp[j]里计算的是组合数!
如果把两个for交换顺序,代码如下:
for (int j = 0; j <= amount; j++) { // 遍历背包容量for (int i = 0; i < coins.size(); i++) { // 遍历物品if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];} }背包容量的每一个值,都是经过 1 和 5 的计算,包含了{1, 5} 和 {5, 1}两种情况。
此时dp[j]里算出来的就是排列数!
-
举例推导dp数组
输入: amount = 5, coins = [1, 2, 5] ,dp状态图如下:

class Solution {public int change(int amount, int[] coins) {int[] dp = new int[amount+1];dp[0]=1;for (int i = 0; i <coins.length; i++) {for (int j = coins[i]; j <=amount ; j++) {dp[j] +=dp[j-coins[i]];}}return dp[amount];}
}
组合总和 Ⅳ
377. 组合总和 Ⅳ - 力扣(LeetCode)
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。
本题题目描述说是求组合,但又说是可以元素相同顺序不同的组合算两个组合,其实就是求排列!
弄清什么是组合,什么是排列很重要。
组合不强调顺序,(1,5)和(5,1)是同一个组合。
排列强调顺序,(1,5)和(5,1)是两个不同的排列。
- 确定dp数组以及下标的含义
dp[i]: 凑成目标正整数为i的排列个数为dp[i]
- 确定递推公式
dp[i](考虑nums[j])可以由 dp[i - nums[j]](不考虑nums[j]) 推导出来。
因为只要得到nums[j],排列个数dp[i - nums[j]],就是dp[i]的一部分。
- dp数组如何初始化
因为递推公式dp[i] += dp[i - nums[j]]的缘故,dp[0]要初始化为1,这样递归其他dp[i]的时候才会有数值基础。
- 确定遍历顺序
个数可以不限使用,说明这是一个完全背包。
得到的集合是排列,说明需要考虑元素之间的顺序。
本题要求的是排列,那么这个for循环嵌套的顺序可以有说法了。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
如果把遍历nums(物品)放在外循环,遍历target的作为内循环的话,举一个例子:计算dp[4]的时候,结果集只有 {1,3} 这样的集合,不会有{3,1}这样的集合,因为nums遍历放在外层,3只能出现在1后面!
所以本题遍历顺序最终遍历顺序:target(背包)放在外循环,将nums(物品)放在内循环,内循环从前到后遍历。
- 举例来推导dp数组
我们再来用示例中的例子推导一下:

class Solution {public int combinationSum4(int[] nums, int target) {int[] dp = new int[target+1];dp[0]=1;for (int j = 0; j <=target ;j++){for (int i = 0; i <nums.length; i++) {if(j>=nums[i]){dp[j] += dp[j-nums[i]];}}}return dp[target]; }
}
相关文章:

算法训练营 day48 动态规划 完全背包 零钱兑换 II 组合总和 Ⅳ
算法训练营 day48 动态规划 完全背包 零钱兑换 II 组合总和 Ⅳ 完全背包 有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物…...
—泛型简单使用)
Java 基础(1)—泛型简单使用
一、泛型定义及作用 泛型是一种编程机制,允许在编写代码时使用参数化类型,以在编译时实现类型安全。 以下是泛型作用: 增强代码可读性和可维护性:通过在代码中使用泛型参数,可以使代码更清晰、更具有可读性和可维护性…...

内存卡损坏了怎么恢复?
内存卡损坏了怎么恢复?现在我们身边有不少电子设备都是用存储卡来存储数据的。一旦需要方便我们直接导出使用。但这存储的数据也不是一定安全的,当我们将内存卡连接到电脑时,难免会碰到病毒、格式化等提示,在这些情况下,可能会导…...
Mysql使用规范(纯技术和实战建议)
1、事务隔级别: (强制):Repeatable-Read(重复读),且不能在会话操作时临时开启隔离级别。 注: Repeatable-Read(重复读)隔离级别解决不了幻读。 可用 show variables l…...
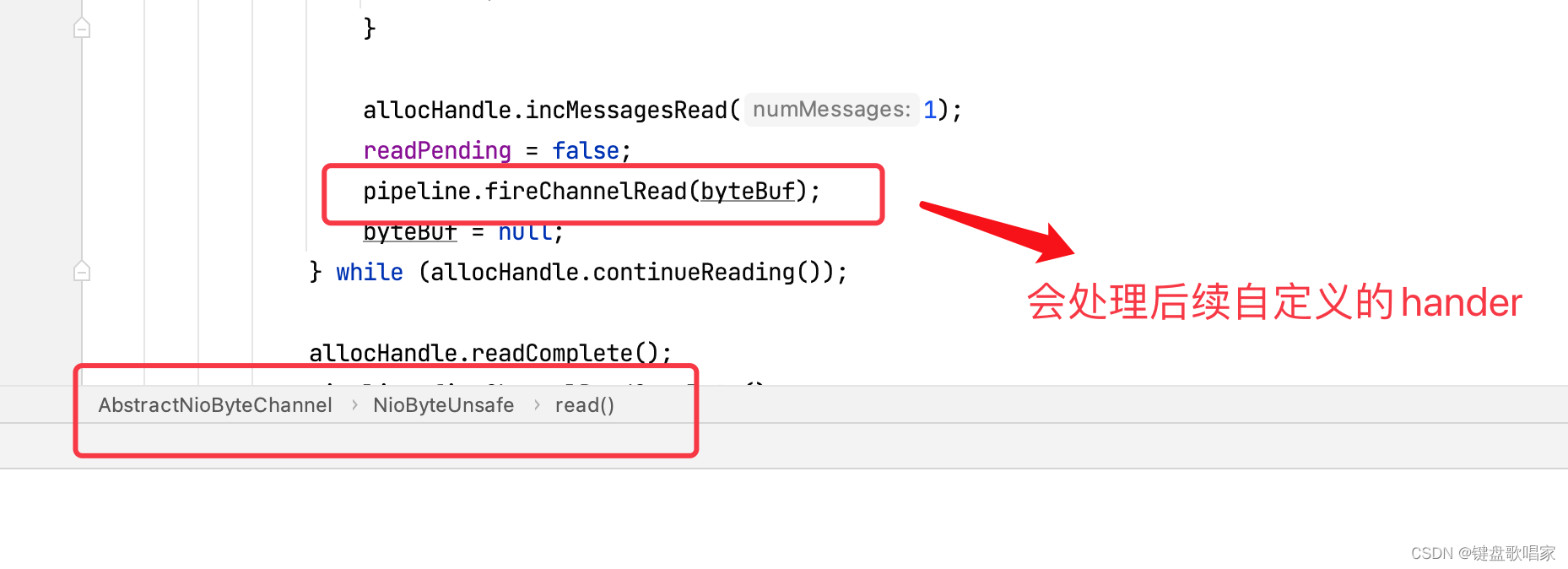
Netty源码解读-EventLoop(二)
一、简介 NioEventLoop的重要组成:Selector、线程、任务队列,他既会处理io事件,也会处理普通任务和定时任务. 1.下面是Selector,注意有两个哦后面会讲 2.下面的爷爷类提供的Thread变量,其实下面发excutor用的就是这个…...

OSI模型详解
今天,我们详解OSI(Open System Inter-connection Reference Model)模型,来看看工业物联网的网络互联和数据互通。 OSI模型 1984年,国际标准化组织(International Organization for Standardization&#…...
Share Creators完成500万美元融资,以工具化手段帮助企业从数字资产管理中解放
近日,总部位于旧金山湾区的初创公司Share Creators宣布完成了新一轮500万美元的融资,投资方为五源资本和福昕PDF。本轮融资主要用于扩大客户基础,并加速在美国、欧洲和亚洲的业务发展。近几年,企业内容及数字资产管理全球市场正在…...
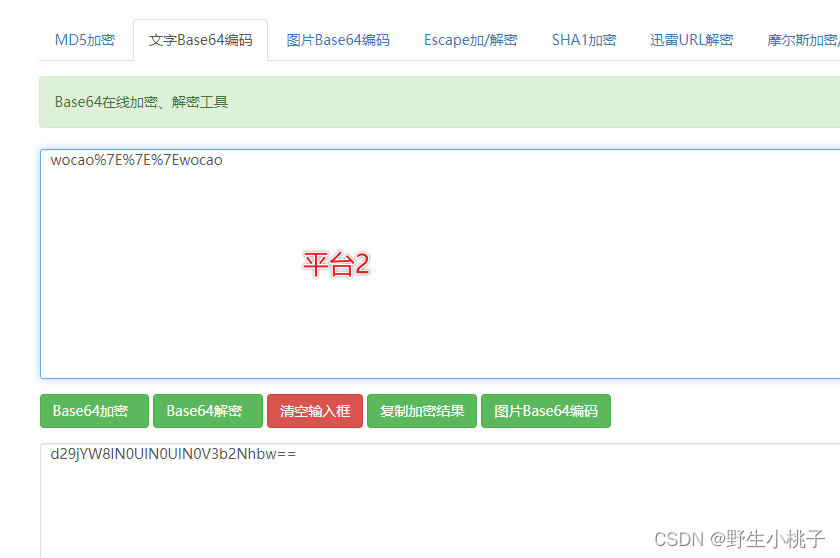
几个Base64编码工具,也有蹊跷
起因 需求:对一段内容进行base64加密,然后通过url的get请求进行发送到后台,由于加密的内容比较少,base64串也不是很长,我认为此方案可行。 于是找了三个base64编码的在线工具,分别是: 平台1&…...

Python|每日一练|排序|递归|字符串|数组|动态规划|单选记录:以特殊格式处理连续增加的数字|正则表达式匹配|地下城游戏
1、以特殊格式处理连续增加的数字(排序) 贡献者:EricLao 给出一串数字, 程序要把数字按照这样的格式输出,把连续增加的数字用 [x-y] 的形式表示,只显示这一组顺序数字的首位两个数字,不连续增…...

Spring Cloud微服务网关Gateway组件
目录 网关简介 什么是Spring Cloud Gateway Spring Cloud Gateway 功能特征 核心概念 工作原理 Spring Cloud Gateway快速开始 环境搭建 集成Nacos 路由断言工厂(Route Predicate Factories)配置 自定义路由断言工厂 过滤器工厂( …...
)
cluster nodes(集群节点)
CLUSTER NODES 复制 自3.0.0起可用。 时间复杂度: O(N)其中N是 Cluster 节点的总数 Redis 集群中的每个节点都有其当前集群配置的视图,由已知节点的集合给出,我们与这些节点的连接状态,它们的标志&…...
【Android学习】下载jar慢和gradle慢的情况
目录 问题出现的原因 解决方法 解决Gradle下载问题:手动安装 解决jar包下载慢问题:更改下载源 问题出现的原因 国内访问谷歌被墙导致访问速度慢或者干脆无法下载 解决方法 解决Gradle下载问题:手动安装 访问官网Gradle | Release Candi…...
下一个排列-力扣31-java
一、题目描述整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。例如,arr [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地&…...

前端面试题
1.HTTP request报文结构是怎样的 1.首行是Request-Line包括:请求方法,请求URI,协议版本,CRLF(换行符) 2.首行之后是若干行请求头,包括general-header,request-header或者entity-hea…...
jsp游戏门户网站系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 jsp 游戏门户网站系统 是一套完善的web设计系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为 TOMCAT7.0,Myeclipse8.5开发,数据库为Mysql,使…...
Git与IDEA强强联合(HTTPS协议连接)
最近在写项目的时候,在台式机和笔记本之间频繁切换,竟然还是用qq传压缩包,我自己都感觉无语,有git这样强大的版本管理工具,我竟然没想起来。然后也没有相关的博文就想来更新一篇。 那么如何使idea和git强强联合呢&…...

leetcode 第二题:两数相加-C语言实现
题目地址 备注: 不要忘记最后一个进位的可能。可以使用typedef,来简化struct的书写 代码实现: #include<stdio.h> #include<stdlib.h>struct listNode {int val;struct listNode* next; };// 使用typedef typedef struct lis…...

【人工智能】PTP网络时钟服务器在智能驾驶里的重要性
【人工智能】PTP网络时钟服务器在智能驾驶里的重要性 【人工智能】PTP网络时钟服务器在智能驾驶里的重要性 一辆宣称具备L4/L5自动驾驶功能的车辆,如果多个激光雷达之间的时间同步不够精确?如果传感器感知数据通过以太网传输到智驾域控制器的延迟不可控…...
【蓝桥杯集训3】二分专题(3 / 5)
目录 二分模板 1460. 我在哪? - 二分答案 哈希表 1221. 四平方和 - 哈希表 / 二分 1、哈希表 2、二分 自定义排序 1227. 分巧克力 - 113. 特殊排序 - 二分模板 l r >> 1 —— 先 r mid 后 l mid1 —— 寻找左边界 —— 找大于某个数的最小值lr…...

在成都的哪个培训机构学习Java好呢?
自从小课06年进入成都这个IT培训市场以来,短短十几年,招过很多学员,也见证过很多机构的起起落落。心中有万分的感慨,总结下来有这几点分享给大家,在选择培训机构时能看清本质,找到适合自己靠谱的机构学Java…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...
