从零开始的数模(二十六)单因素方差分析
目录
一、概念
1.1相关概念
1.2用途
1.3数据要求:独立性/正态性/方差齐性
1.4步骤
编辑1.5专业名词
二、基于python的单因素方差分析
2.2单因素方差分析的作用
一、概念
1.1相关概念
单因素方差分析是一种常用的统计分析方法,它用于比较一个因素对于连续性变量的影响。它通常用于研究一个自变量对一个因变量的影响,并比较不同组之间的均值是否显著不同。
在单因素方差分析中,数据被分成多个组,每个组都有自己的均值和方差。该方法基于比较这些组之间的方差来确定它们是否来自同一个总体。如果方差差异很小,则我们可以假定它们来自同一个总体,反之,则我们可以得出结论,这些组之间有显著的差异。
单因素方差分析通常用于实验设计,特别是在需要比较多个处理组时。该方法还可以用于比较不同组的表现,例如比较不同班级的平均分数或比较不同治疗方案的疗效。
单因素方差分析的假设包括:各组数据来自正态分布总体、各组方差相等、各组之间相互独立。该方法可以使用统计软件进行分析。常用的单因素方差分析方法包括单因素方差分析和方差齐性检验、多重比较方法(例如Tukey方法)等。
1.2用途
用来研究一个控制变量的不同水平是否对观测变量产生了显著影响。
人话:比较不同组别的平均值有无差异, 只有一个因素发生变化
原理:用来计算组间差异与组内差异的比值
若组间差异与组内差异的对比比值较大,则认为单因素方差分析的结果显著。即意味着不同组别的均值存在显著差异
1.3数据要求:独立性/正态性/方差齐性
1.因变量要为连续数值型变量,即共用一个坐标轴,可以取到任何数值
2.每一组对的变量都需要服从正态分布(可放宽)
3.组别间的方差相等(可放宽)
4.组别个数≥3组
1.4步骤
现在假定一个因素B具有c个水平的因变量进行方差分析检验,例如上面提到的工厂轧制设备是因素,分别试验轧制了10块板材是水平。
 1.5专业名词
1.5专业名词

听不懂吧,上例题
二、基于python的单因素方差分析
2.1所用库
import pandas as pd
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lmstatsmodels是一个Python包,它为scipy提供了对scipy的补充。 统计计算,包括描述性统计和估计 以及统计模型的推理。
import numpy as np
from scipy import stats
import statsmodels.api as sm
from statsmodels.formula.api import ols# 生成示例数据,有3个组,每个组有5个观测值
group1 = [10, 12, 14, 15, 18]
group2 = [8, 9, 11, 14, 16]
group3 = [6, 7, 9, 12, 14]# 将数据合并成一个数组
data = np.array(group1 + group2 + group3)# 根据组信息创建因子
factors = np.array(['group1'] * 5 + ['group2'] * 5 + ['group3'] * 5)# 执行单因素方差分析
F, p = stats.f_oneway(group1, group2, group3)# 输出ANOVA结果
print('F值:', F)
print('p值:', p)# 使用statsmodels创建ANOVA表
model = ols('data ~ factors', data=dict(data=data, factors=factors)).fit()
anova_table = sm.stats.anova_lm(model, typ=2)
print(anova_table)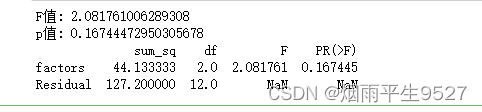
anova_lm是Python中statsmodels包中的函数,用于执行方差分析(ANOVA)并返回方差分析表的结果。该函数返回的参数包括:
df:自由度的数量,即方差分析中每个因素和误差的自由度。
sum_sq:平方和,即方差分析中每个因素和误差的平方和。
mean_sq:均方,即平方和除以相应的自由度,用于计算方差。
F:F统计量,即均方之比,用于检验因素是否显著影响结果变量。
PR(>F):p值,即F统计量的概率,用于检验因素是否显著影响结果变量。
eta_sq:方差解释比,即因素对总方差的解释程度。
omega_sq:Omega方差解释比,是对方差解释比的修正,考虑了样本量和自由度的影响。
此外,anova_lm还可以返回resid和resid_std,它们分别代表残差和标准化残差。
在方差分析中,我们可以使用PR值(p-value)来检测因素是否对结果变量具有显著影响。PR值是在假定因素对结果变量没有影响的情况下,观察到的数据样本出现当前统计结果或更极端结果的概率。
具体地,PR值是在计算F统计量之后,利用F分布的概率密度函数来计算得出的。我们将计算得到的F统计量与F分布进行比较,得到一个概率值(PR值),该值表明了出现这样极端的F统计量的概率。如果PR值小于显著性水平(通常为0.05),则我们可以拒绝假设,认为因素对结果变量具有显著影响。
需要注意的是,PR值只能告诉我们我们是否可以拒绝假设,不能证明假设成立。此外,PR值只能在当前样本中进行统计推断,并不代表总体情况。因此,在进行实验设计和数据分析时,我们需要合理设计样本,以增强推论的可靠性。残差(residual)指的是实际观测值与模型预测值之间的差异或偏差。在回归分析中,残差是因变量和自变量之间的线性关系无法完全解释因变量的部分,也可以理解为模型中未被解释的部分。残差是一个重要的概念,因为它们提供了评估模型拟合程度的一种方法。
2.2单因素方差分析的作用
单因素方差分析(One-way ANOVA)是一种用于比较三个或更多组均值是否相等的统计方法。在单因素方差分析中,我们将数据分成多个组,并将每个组的均值与整体均值进行比较,以确定组间差异是否显著。
单因素方差分析的作用在于:
确定不同组之间的均值是否有显著差异。单因素方差分析可以帮助我们确定组间差异是否显著,以及哪些组之间存在显著差异。这有助于我们更好地了解数据,并提供了可能的解释。
确定误差的大小。单因素方差分析可以帮助我们评估数据的可靠性,通过计算组间方差和误差方差来确定误差的大小。较小的误差可能表明数据更加一致和可靠,而较大的误差可能表明数据存在更多的随机误差或测量误差。
选择适当的统计测试。单因素方差分析可以帮助我们确定是否需要使用其他的统计方法来处理数据。例如,如果组间差异不显著,我们可以使用t检验来比较两个组之间的差异;如果组间差异显著,我们可以使用多重比较或后续分析来确定哪些组之间存在显著差异。
提供基础数据分析的统计框架。单因素方差分析是基本的数据分析方法之一,可以提供基本的统计框架和思考方式,有助于我们更好地理解其他复杂的数据分析技术。
相关文章:

从零开始的数模(二十六)单因素方差分析
目录 一、概念 1.1相关概念 1.2用途 1.3数据要求:独立性/正态性/方差齐性 1.4步骤 编辑1.5专业名词 二、基于python的单因素方差分析 2.2单因素方差分析的作用 一、概念 1.1相关概念 单因素方差分析是一种常用的统计分析方法,它用于比较一个因…...

C++变量类型
目录 一、c中的变量定义 二、c中的变量声明 三、c中的左值和右值 一、c中的变量定义 变量定义就是告诉编译器在何处创建变量的存储,以及如何创建变量的存储。 变量定义指定一个数据类型,并包含了该类型的一个或多个变量的列表,如下所示&…...

win10 安装 vs2015(社区版本)以及opencv-4.5.5
一、下载vs2015以及opencv-4.5.5从https://msdn.itellyou.cn/ 网站下载vs2015(社区版本)从https://opencv.org/releases/网站下载opencv-4.5.5二、安装vs2015和opencv-4.5.5解压后双击exe安装文件,完成安装(默认)双击下…...

867. 转置矩阵
给你一个二维整数数组 matrix, 返回 matrix 的 转置矩阵 。矩阵的 转置 是指将矩阵的主对角线翻转,交换矩阵的行索引与列索引。示例 1:输入:matrix [[1,2,3],[4,5,6],[7,8,9]]输出:[[1,4,7],[2,5,8],[3,6,9]]示例 2&a…...

Datawahle组队学习——妙趣横生大数据 Day1
妙趣横生大数据 Day1[妙趣横生大数据 Juicy Big Data](https://datawhalechina.github.io/juicy-bigdata/#/?id妙趣横生大数据-juicy-big-data)一、大数据概述大数据——第三次信息化浪潮大数据概念大数据应用大数据关键技术二、Hadoop背景介绍特性项目架构实验1. 准备工作2. …...
网友眼中越老越吃香的行业,果然是风向变了!
越老越吃香的行业,一直都是被热议的话题。对于年轻人来说,找到一个适合自己的并且具有前景的工作,不是一件容易的事情。 最近,看到有人在平台上问相关的问题,本着认真看一看的态度点进去,却差点被热评第一…...
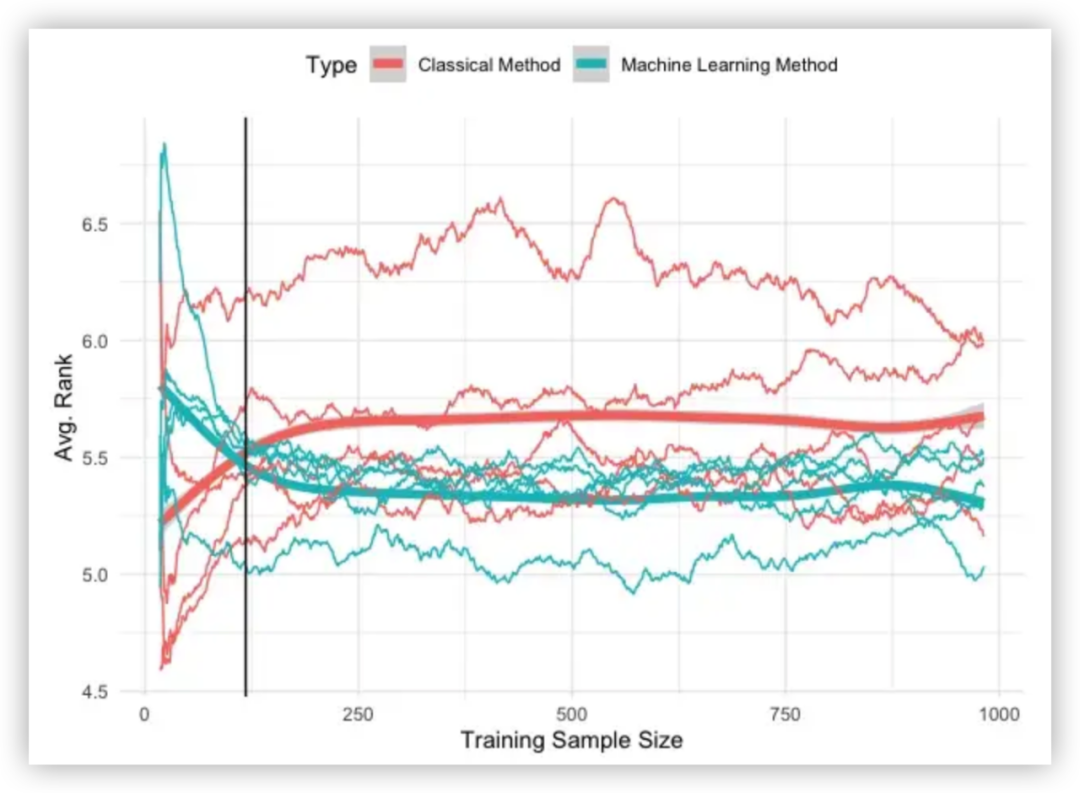
为什么时间序列预测这么难?本文将给你答案
机器学习和深度学习已越来越多应用在时序预测中。ARIMA 或指数平滑等经典预测方法正在被 XGBoost、高斯过程或深度学习等机器学习回归算法所取代。 尽管时序模型越来越复杂,但人们对时序模型的性能表示怀疑。有研究表明,复杂的时序模型并不一定会比时序…...
STC15系列单片机通过串口多字节数据读写EEPROM操作
STC15系列单片机通过串口多字节数据读写EEPROM操作📌相关篇《STC15系列单片机EEPROM读写示例》 ⛳手册勘误信息注意事项 ⚡在手册上面描述STC15F2K60S2及STC15L2K60S2系列单片机内部EEPROM还可以用MOVC指令读,但此时首地址不再是0000H,而是程…...

计算机网络-ip数据报
在图中,网络层包含了四种协议:ARP、IP、ICMP、IGMP,由上下关系表明,ARP为IP协议服务,IP为ICMP和IGMP服务。 IP数据报格式 此处不区分数据报和分组的概念:当数据部分过长时,将数据部分拆分&…...

从零开始学C
以下是 该如何学习C语言的【思维导图】以及部分重点知识点的【博客链接】。其实C语言并不难,难的是没有人去教,没有耐心去学。不知道从哪下手学习,我将C的知识点做成一个思维导图,以供迷茫的小白参考,哪里不会…...
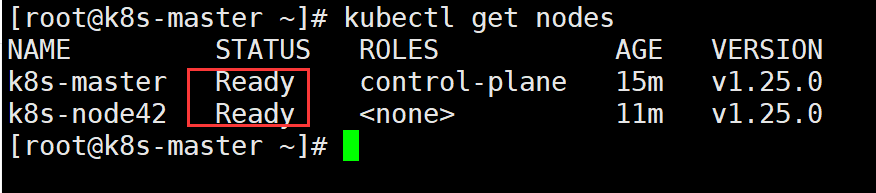
【云原生】手把手带你从零开始搭建kubernetes最新版本实战
文章目录前言一. 实验环境二. k8s 的介绍三 . k8s的安装3.1 搭建实验环境3.1.1 硬件层面的要求3.1.2 软件层面环境配置3.2 docker的安装3.2.1 搭建docker3.2.2 部署 cri-dockerd3.3 部署k8s3.3.1 配置添加阿里云的yum源3.3.2 安装kubeadm kubelet kubectl3.3.3 k8s-master节点初…...

trivy os软件包扫描原理分析
具体可以基于之前的博客来做 基于trivy获取基础镜像 参数修改一下: cliOpt.ListAllPkgs true 结果中会带有如下格式的结果: "Results":[{"Target":"192.168.1.94:443/test22/centos:7 (centos 7.9.2009)","Clas…...

算法训练营 day48 动态规划 完全背包 零钱兑换 II 组合总和 Ⅳ
算法训练营 day48 动态规划 完全背包 零钱兑换 II 组合总和 Ⅳ 完全背包 有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物…...
—泛型简单使用)
Java 基础(1)—泛型简单使用
一、泛型定义及作用 泛型是一种编程机制,允许在编写代码时使用参数化类型,以在编译时实现类型安全。 以下是泛型作用: 增强代码可读性和可维护性:通过在代码中使用泛型参数,可以使代码更清晰、更具有可读性和可维护性…...

内存卡损坏了怎么恢复?
内存卡损坏了怎么恢复?现在我们身边有不少电子设备都是用存储卡来存储数据的。一旦需要方便我们直接导出使用。但这存储的数据也不是一定安全的,当我们将内存卡连接到电脑时,难免会碰到病毒、格式化等提示,在这些情况下,可能会导…...
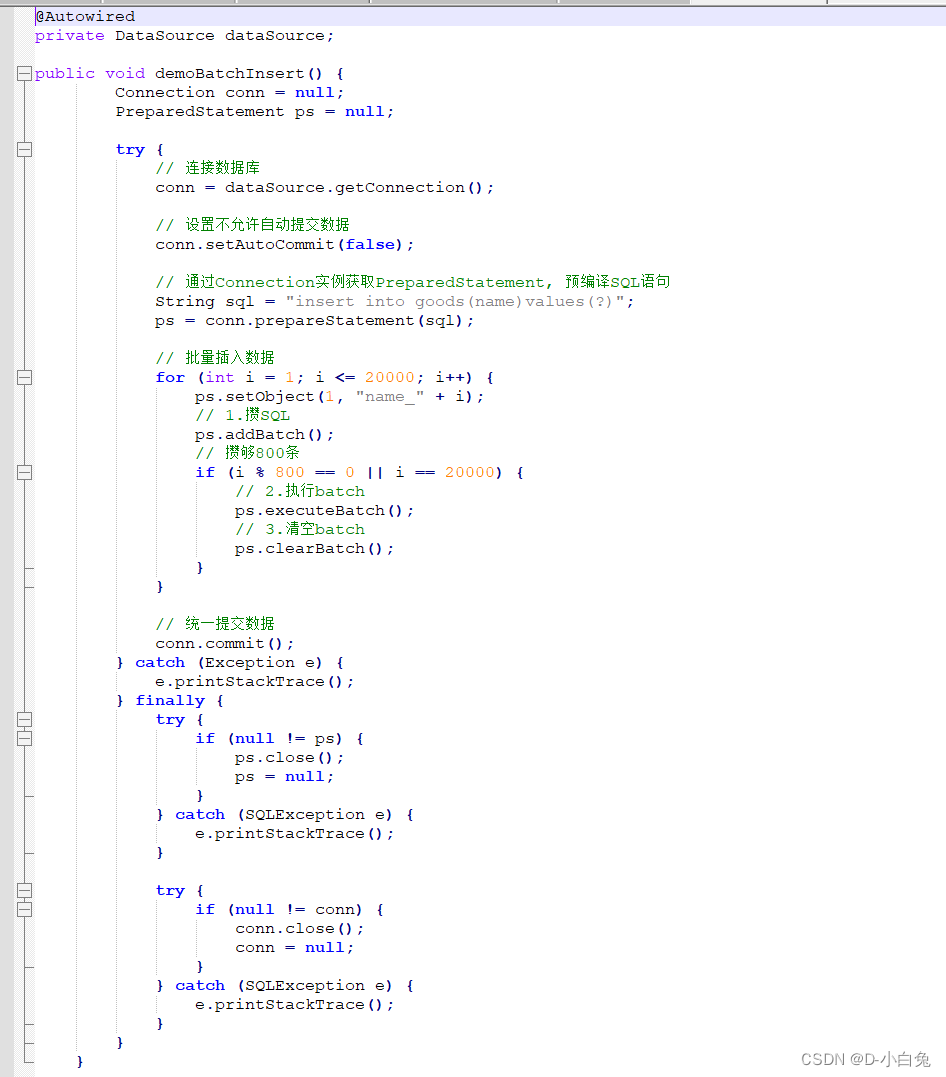
Mysql使用规范(纯技术和实战建议)
1、事务隔级别: (强制):Repeatable-Read(重复读),且不能在会话操作时临时开启隔离级别。 注: Repeatable-Read(重复读)隔离级别解决不了幻读。 可用 show variables l…...
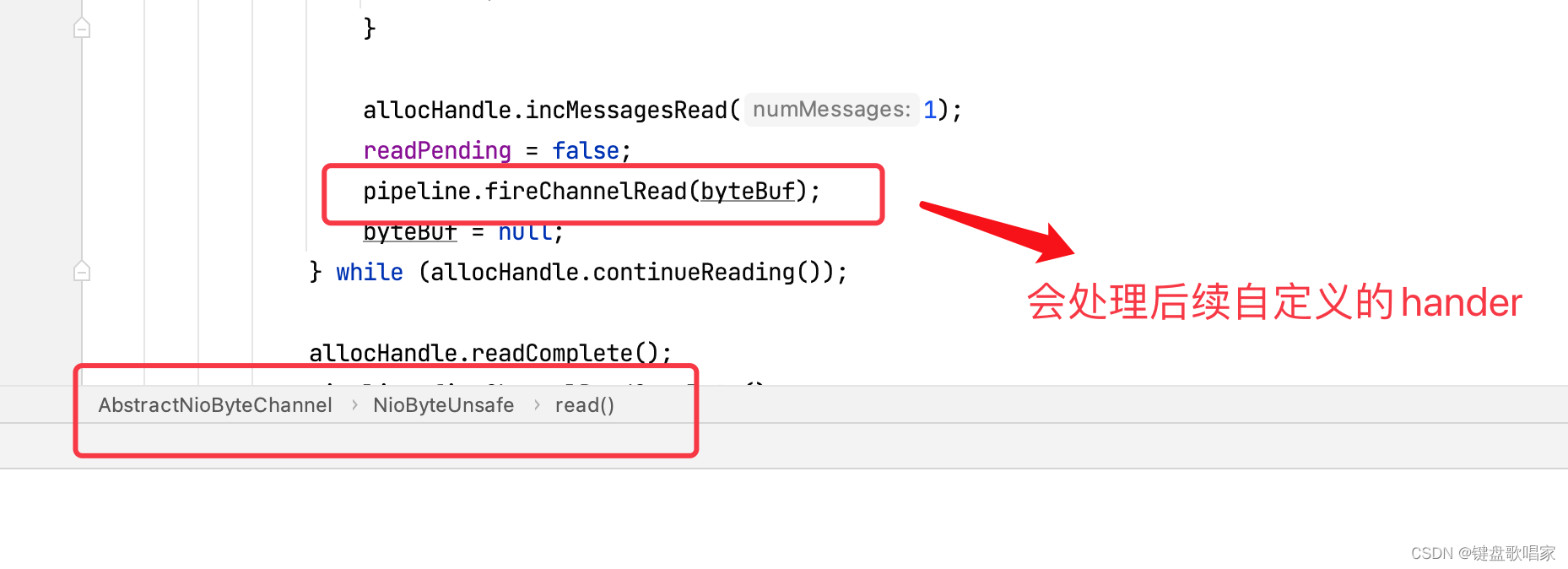
Netty源码解读-EventLoop(二)
一、简介 NioEventLoop的重要组成:Selector、线程、任务队列,他既会处理io事件,也会处理普通任务和定时任务. 1.下面是Selector,注意有两个哦后面会讲 2.下面的爷爷类提供的Thread变量,其实下面发excutor用的就是这个…...

OSI模型详解
今天,我们详解OSI(Open System Inter-connection Reference Model)模型,来看看工业物联网的网络互联和数据互通。 OSI模型 1984年,国际标准化组织(International Organization for Standardization&#…...
Share Creators完成500万美元融资,以工具化手段帮助企业从数字资产管理中解放
近日,总部位于旧金山湾区的初创公司Share Creators宣布完成了新一轮500万美元的融资,投资方为五源资本和福昕PDF。本轮融资主要用于扩大客户基础,并加速在美国、欧洲和亚洲的业务发展。近几年,企业内容及数字资产管理全球市场正在…...
几个Base64编码工具,也有蹊跷
起因 需求:对一段内容进行base64加密,然后通过url的get请求进行发送到后台,由于加密的内容比较少,base64串也不是很长,我认为此方案可行。 于是找了三个base64编码的在线工具,分别是: 平台1&…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...
