数据分析-深度学习 Tensorflow Day6
我们需要解决的问题:
1: 什么是bp 神经网络?
2:理解bp神经网络需要哪些数学知识?
3:梯度下降的原理
4: 激活函数
5:bp的推导。
1.什么是bp网络?
引用百度知道回复:
“我们最常用的神经网络就是BP网络,也叫多层前馈网络。BP是back propagation的所写,是反向传播的意思。我以前比较糊涂,因为一直不理解为啥一会叫前馈网络,一会叫BP(反向传播)网络,不是矛盾吗?其实是这样的,前馈是从网络结构上来说的,是前一层神经元单向馈入后一层神经元,而后面的神经元没有反馈到之前的神经元;而BP网络是从网络的训练方法上来说的,是指该网络的训练算法是反向传播算法,即神经元的链接权重的训练是从最后一层(输出层)开始,然后反向依次更新前一层的链接权重。因此二者并不矛盾,只是我没有理解其精髓而已”
随便提一下BP网络的强大威力:
1)任何的布尔函数都可以由两层单元的网络准确表示,但是所需的隐藏层神经元的数量随网络输入数量呈指数级增长;
2)任意连续函数都可由一个两层的网络以任意精度逼近。这里的两层网络是指隐藏层使用sigmoid单元、输出层使用非阈值的线性单元;
3)任意函数都可由一个三层的网络以任意精度逼近。其两层隐藏层使用sigmoid单元、输出层使用非阈值的线性单元。
2:理解bp神经网络需要哪些数学知识?
需要知道什么是导数,什么是偏导? 什么是链式推导?
导数:
导数的求法示范: f(x)=2x 的导数是 2
f(x)=x*x 的导数是 2x
f(x)=x*x*x +3*x+4 的导数是 3(x*x)+3
导数的具体的定义入门 及推导过程 通俗易懂的导数基础讲义_百度文库
偏导:
偏导的定义:也即是原来只有一个参数的f(x) 成为了多个参数 例如f(x,y)
求对x的偏导时 将y当常数
求y的偏导时 将x当常数。
推导示范:
f(x,y)=2x*x + 3y+4
对x的导数: 4x (没有x的常数项为0)
对y的导数: 3
看下偏导入门 偏导数的定义及其计算法_图文_百度文库
链式推导:
示范:
f(g(x))=(g(x))*(g(x))
g(x)=3x
则f(g(x))对x的导数为=f(g(x))的导数 * 个g(x)的导数
= (2*(g(x)))*3
= 6*(g(x))
= 18x
以上 即是需要理解的数学基础。
3:梯度下降的原理
梯度下降是什么呢? 当我们用神经网络算出一个实际输出O。 这个值和期望输出d的差值 即是损失函数(就是一个和你想要的结果差距有多大)
因为在数学中不好算负值 , 所以我们把差值平方, 同时为了求导方便 对这个平方差值 乘以1/2
所以最后的损失函数就成了:
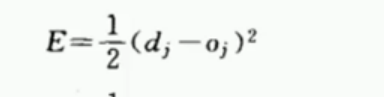
这个函数的曲线是:

以上 就是损失函数: 我们知道,这个函数,当他的导数为0的时候, 它的值最小。 所以我们在每次求出损失函数时,去求导 根据这个导数去改变权重,从而努力使这个导数接近零。
跑下 最后的代码调试下,或者去百度搜索下
4:激活函数
本文不讨论激活函数的具体原理,以后会专门介绍。 只需要知道,加入激活函数是用来 加 入非线性因素的,解决线性模型所不能解决的问题。
推荐阅读 形象的解释神经网络激活函数的作用是什么?
5:bp的推导
本次推导是对 通俗理解神经网络BP传播算法的笔记, 但是原文写的有些错误和一些地方没有说明 导致 萌新不易理解。本文会将出现的问题补齐:
主要问题有:
1: 链式推导写的太混乱 。以下是手推过程:下面的

2:求出来了代价函数对权值的偏导后 没有说明怎么应用
代价函数改变公式在下面:

在这本文 比例系数 为1 。多看几遍这个 才能理解最后代码里的权值改变:
最后 是它的 代码:
importnumpyasnpdefnonlin(x,deriv=False):if(deriv==True):returnx*(1-x)#如果deriv为true,求导数return1/(1+np.exp(-x))X=np.array([[0.35],[0.9]])#输入层y=np.array([[0.5]])#输出值np.random.seed(1)W0=np.array([[0.1,0.8],[0.4,0.6]])W1=np.array([[0.3,0.9]])print'original ',W0,'\n',W1forjinxrange(100):l0=X#相当于文章中x0l1=nonlin(np.dot(W0,l0))#相当于文章中y1l2=nonlin(np.dot(W1,l1))#相当于文章中y2l2_error=y-l2Error=1/2.0*(y-l2)**2print"Error:",Errorl2_delta=l2_error*nonlin(l2,deriv=True)#this will backpack#print 'l2_delta=',l2_deltal1_error=l2_delta*W1;#反向传播l1_delta=l1_error*nonlin(l1,deriv=True)W1+=l2_delta*l1.T;#修改权值W0+=l0.T.dot(l1_delta)printW0,'\n',W1相关文章:

数据分析-深度学习 Tensorflow Day6
我们需要解决的问题:1: 什么是bp 神经网络?2:理解bp神经网络需要哪些数学知识?3:梯度下降的原理4: 激活函数5:bp的推导。1.什么是bp网络?引用百度知道回复:“我们最常用的…...

leaflet 设置多个marker,导出为一个geojson文件(066)
第066个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中使用L.marker设置多个markers, 通过数据重组,导出为geojson文件。 这里面 ayer instanceof L.Marker 是一个很重要的判断条件,可以灵活地去运用。 直接复制下面的 vue+openlayers源代码,操作2分钟即可…...

企业与第三方供应商合作时,会存在哪些安全风险?
随着现代社会的发展,企业供应链、产业供应链已日渐成熟。其中,供应商与企业的关系也由最初的纯粹买卖关系发展成了合作伙伴关系。在整个供应链体系中,供应商与其受众承担着供应链中环环相扣的责任,可以说,企业安全的薄…...

技术源自洛克希德·马丁,光场XR眼镜FYR解析
专注于医疗场景的一家XR眼镜厂商FYR(全称:FYR Medical)近期亮相,并宣布完成了260万美元A轮融资,本轮融资由NuVasive领投,资金将用于开发世界上第一个XR光场“放大镜”类产品。据青亭网了解,NuVa…...
(动态规划打表))
剑指 Offer 10- II. 青蛙跳台阶问题(LeetCode 70. 爬楼梯)(动态规划打表)
题目: 链接:剑指 Offer 10- II. 青蛙跳台阶问题;LeetCode 70. 爬楼梯 难度:简单 相关博文:剑指 Offer 10- I. 斐波那契数列(动态规划打表) 一只青蛙一次可以跳上1级台阶,也可以跳上…...
--文件的压缩Terser(js/css/html) Tree Shaking)
webpack(高级)--文件的压缩Terser(js/css/html) Tree Shaking
webpack Terser Terser是一个javascript的解释(Parser),Mangler(绞肉机) /Compressor(压缩机)的工具集 早期我们会使用uglify-js来压缩,丑化我们的javascript代码 但是目前已经不在维护 并且不支持ES6语法 Terser是从uglify-es fork 过来的 也就是说 Terser可以帮…...

做软文发布需要注意哪些细节?
软文发布是一种有效的网络营销和推广活动,它以媒体等形式把产品信息植入到软文报道或新闻中,进行心理暗示和引导销售,进行正面宣传以及促进销售的新型网络营销方式,它不但能够有效地推行产品宣传、也能有效地提高网络曝光率&#…...

【Python】一篇文章读懂yield基本用法
这一次,田辛老师想通俗易懂地解释一下Python中的yield功能。 本文要说明以下四个问题: yield是什么什么是迭代器和生成器yield的基本用法如何使用yield from 用真正简单的方法讲解yield并不容易。 我想,就算你不懂yield语句,也…...

Docker getting started
系列文章目录 Docker 概述 Docker getting started 文章目录系列文章目录前言一、容器及镜像的概念二、容器化一个应用三、更新应用四、分享应用五、持久化数据存储volume mount 和 bind mount比较Container volumesbind mounts六、跨多容器的应用七、Docker 其它八、Docker 图…...

【Uniapp使用遇到问题合集】
Uniapp使用遇到问题合集问题一跳转页面后无法进行滑动/滚动的操作描述解决方法问题一 跳转页面后无法进行滑动/滚动的操作 描述 如题,实际操作是我在uniapp自带的组件uni-popup弹出层中加入了一个点击事件,点击后可跳转到指定的页面 但实际运行中出现了跳转过后页面过长时无…...

宝塔面板破解最新教程
宝塔,让运维简单高效。面板支持Linux与Windows系统。一键配置:LAMP/LNMP、网站、数据库、FTP、SSL,通过Web端轻松管理服务器。今天考高分网就简单说一下BT宝塔面板专业版最新破解教程。 网地址:https://www.bt.cn/ 网上的破解版一般分为两种,一种是直接…...
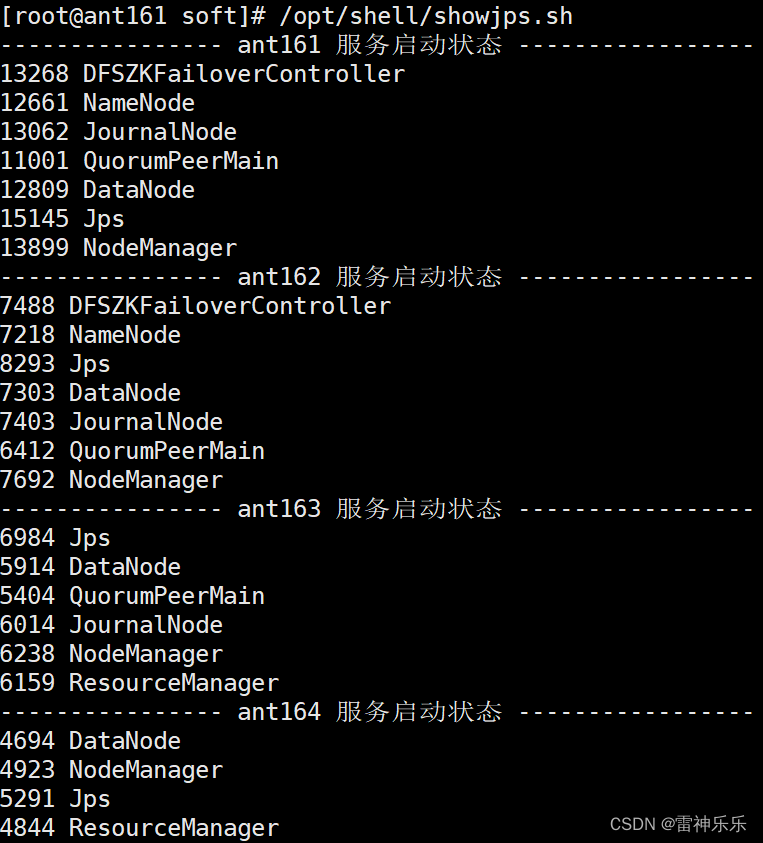
基于zookeeper的Hadoop集群搭建详细步骤
目录 一、一些基本概念 二、集群配置图 三、Hadoop高可用集群配置步骤 1.在第一台虚拟机解压hadoop-3.1.3.tar.gz到/opt/soft/目录 2.修改文件名、属主和属组 3.配置windows四台虚拟机的ip映射 4.修改hadoop配置文件 (1)hadoop-env.sh (2)workers (3)crore-site.xml …...

职称有哪些意义?如何提升职称?
每年我们会看到很多人都会努力地提升自己的职称,那么为什么大家都想要晋升职称?在这里余老师说说他的作用,您可以参考一下。 一、个人金钱方面的提升 工资。职称直接关联的就是涨工资了。正常情况下,职称和工资是一一对应的了,…...

mulesoft MCIA 破釜沉舟备考 2023.02.15.09
mulesoft MCIA 破釜沉舟备考 2023.02.15.09 1. According to MuleSoft, which deployment characteristic applies to a microservices application architecture?2. Refer to the exhibit.3. Mule application A receives a request Anypoint MQ message REQU with a payload…...

【项目实战】@ConditionalOnProperty注解让我少写了一些if判断
一、需求说明 本机启动含有XXL-job的工程,发现每次都会进行XXL-job的init的动作。这会导致本机每次启动都会把自己注册到XXL-job的服务端。但是我明明本地调试的功能不想要是编写定时任务,于是想了下,是否可以设计一个开关,让本机…...

SQL中的游标、异常处理、存储函数及总结
目录 一.游标 格式 操作 演示 二.异常处理—handler句柄 格式 演示 三.存储函数 格式 参数说明 演示 四.存储过程总结 一.游标 游标(cursor)是用来存储查询结果集的数据类型,在存储过程和函数中可以使用游标对结果集进行循环的处理。游标的使用包括游标的声明、OPEN、…...

Splashtop:支持M1/M2芯片 Mac 电脑的远程控制软件
M1和M1芯片的Mac电脑现在越来越多了。M1和M2的强大性能,让使用者们办公、娱乐如虎添翼。 M1 芯片于2020年11月11日推出,是Apple 首款专为Mac打造的芯片,拥有格外出色的性能、众多的功能,以及令人惊叹的能效表现。M1 也是Apple 首款…...

实验十三、阻容耦合共射放大电路的频率响应
一、题目 利用 Multism 从以下几个方面研究图1所示的阻容耦合共射放大电路的频率响应。图1阻容耦合共射放大电路图1\,\,阻容耦合共射放大电路图1阻容耦合共射放大电路(1)设 C1C210μFC_1C_210\,\textrm{μF}C1C210μF,分别测试它们所确定…...
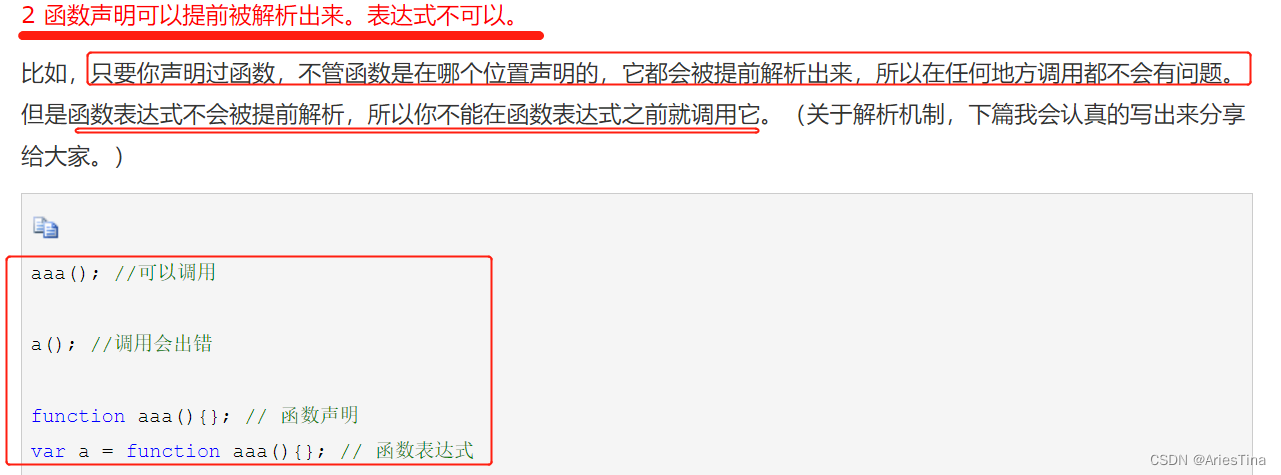
【每天进步一点点】函数表达式和函数声明
函数声明 function 函数名(){} 函数声明会被率先读取。 函数声明后不会立即执行,会在我们需要的时候调用到。 由于函数声明不是一个可执行语句,所以不以分号结束。 函数表达式 表达式赋值给了一个变量 const 变量名 functi…...

JavaScript void
文章目录JavaScript voidjavascript:void(0) 含义href"#"与href"javascript:void(0)"的区别JavaScript void javascript:void(0) 含义 我们经常会使用到 javascript:void(0) 这样的代码,那么在 JavaScript 中 javascript:void(0) 代表的是什么…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...
