leetcode 困难 —— 数字 1 的个数(简单逻辑题)
(害,做题是真的慢,这面试给我这题我估计就傻了)
题目:
给定一个整数 n,计算所有小于等于 n 的非负整数中数字 1 出现的个数。
题解:
首先看看整数范围 0 <= n <= 10^9 不能遍历(不过这也肯定不会简单到遍历)
比如存在一个数 25103,我们应该从哪里下手呢
我们是否可以考虑,各个位置上(个位,十位…)存在 1 的情况数量,然后相加得到结果呢
我们先考虑一般情况, 数字 xxx 4 yy,百位上,存在 1 的情况数量怎么算
想一想 100,101,102,…,199是不是百位上都是 1,这种情况 100 种
在考虑一下百位前面的 xxx,是不是总共有 (xxx + 1) * 100 种
(假设 xxx 是 123,那么 123 1 yy 有 100 种,122 1 yy 有 100 种 … 000 1 yy 有 100 种)
接下来稍微扩展一下一般情况,那数字 xxxx 4 y 十位上的情况是不是就是 (xxxx + 1) * 10 种
接下来考虑特殊情况,如果数字 xxx 1 yy 百位上是 1,这怎么算呢
当前面是 xxx 时,百位上为 1 的情况只有 yy 种,但是当前面是 (xxx - n) 时,情况有 100 种
所以是不是情况是 xxx * 100 + yy 种
(假设 xxx 是 123,那么 123 1 yy 有 yy种,但 122 1 yy,则没有这种限制,有 100 种)
再一种特殊情况,如果数字 xxx 0 yy 百位上是 0,这怎么算呢
其实就是当前面是 xxx 时,百位上为 1 的情况为 0 种,当前面是 (xxx - n) 时,情况也都有 100 种
所以情况是 xxx * 100 种
接下来写代码就行了
class Solution {
public:int countDigitOne(int n) {int res = 0;int f = 1;int nn = n / 10;while(nn != 0) {nn = nn / 10;f = f * 10;}int flag = 0;while(f != 0) {int t = n / f;n = n % f;if(t == 1) {res = res + n + 1 + flag * f;}else if(t == 0) {res = res + flag * f;}else {res = res + (flag + 1) * f;}flag = flag * 10 + t;f = f / 10;}return res;}
};
相关文章:
)
leetcode 困难 —— 数字 1 的个数(简单逻辑题)
(害,做题是真的慢,这面试给我这题我估计就傻了) 题目: 给定一个整数 n,计算所有小于等于 n 的非负整数中数字 1 出现的个数。 题解: 首先看看整数范围 0 < n < 10^9 不能遍历࿰…...

关于JSON
<!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title></title> </head> <body> <script> /* 1、JSON的英文全称:Java…...
Apifox-接口调用、自动化测试工具
Apifox简介 Apifox 的定位是Postman Swagger Mock JMeter,具有API文档管理、API调试、API Mock、API 自动化测试等功能。可以通过一种工具解决之前使用多种工具的数据同步问题。高效、及时、准确! 安装 Apifox的安装非常方便,直接下载安…...
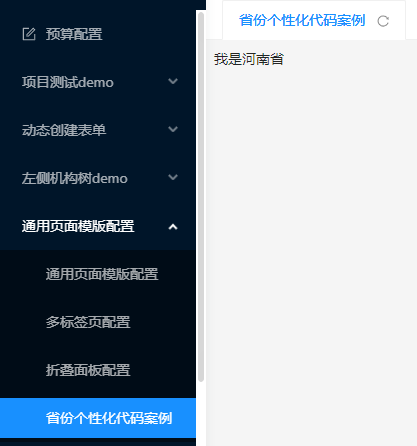
Vue一个项目兼容每个省份的个性化需求
开发环境及打包指令 后拼上省份区划"serve:henan": "yarn && vue-cli-service serve -o --encryptSM2 --zone41","serve:hunan": "yarn && vue-cli-service serve -o --encryptSM2 --zone43","serve:guizhou&quo…...

npm install报错 npm ERR! 的解决办法
以下是四种常见的npm ERR及解决方式错误一、npm ERR! A complete log of this run can be found in:npm ERR!C:\Users\nanyi\AppData\Roaming\npm-cache_logs\2021-09-17T08_58_23_413Z-debug.l查看错误日志,错误日志就在上面展示的C:\Users…这里如果发现错误日志里…...
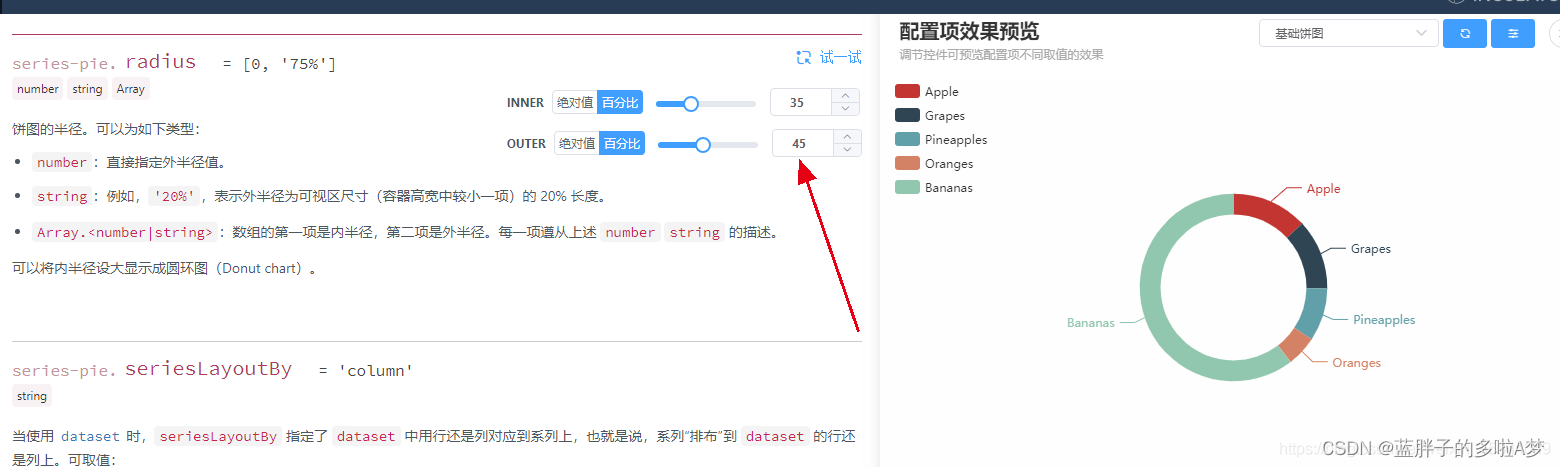
echarts修改饼图,环形图的圆环宽度,大小
echarts修改环形图的圆环宽度,大小 环形图圆环的大小需要通过series-pie. radius属性来修改 radius 饼图的半径。 Array.<number|string>:数组的第一项是内半径,第二项是外半径。每一项遵从上述 number string 的描述。 把数组的第…...

小白系列Vite-Vue3-TypeScript:010-封装svg
上一篇我们介绍了ViteVue3TypeScript项目中mockjs的安装和配置i。本篇我们来介绍封装SVG图标组件。svg特征Preloading所有图标都是在项目运行时生成的,只需要操作一次dom即可。高性能内置缓存,仅在文件被修改时才会重新生成。安装插件vite-plugin-svg-ic…...

卷严重、难度高、激励少,如何适应空投市场新变化
自从空投交互从2020年开始之后,不少人都开始加入到空投交互的行列中,一些项目也因为“格局”的因素,在项目正式上线前都会给早期参与者空投代币,以此吸引大家的关注。但是在越来越多的人加入到撸空投行列之中后,现在整…...

基于Java与JSP的文件上传和下载
概念 当用户在前端页面点击文件上传后,用户上传的文件数据提交给服务器端,实现保存。 文件上传步骤 提交方式: 提供form表单,method必须是post。因为post请求无数据限制。 <form method"post"></form>…...
Gromacs中的g_mmpbsa计算带电底物与蛋白的结合能不准确
g_mmpbsa计算带电底物与蛋白的结合能总是不准确 TOC 在做的两个项目中,利用g_mmpbsa计算带电底物与蛋白的结合能结果非常不可靠,底物带两个硫酸根离子,g_mmpbsa在计算带电的底物与酶的结合能时总是不准确,因此后续若底物带电&…...
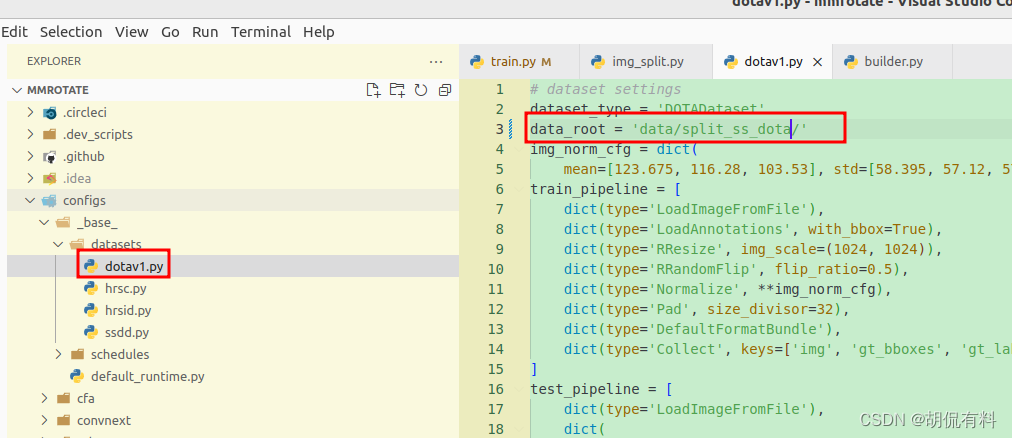
【mmrotate】旋转目标检测之训练DOTA数据集
every blog every motto: You can do more than you think. https://blog.csdn.net/weixin_39190382?typeblog 0. 前言 mmrotate训练DOTA数据集记录 1. 正文 1.1 数据准备 数据介绍部分,参考DOTA数据介绍,官方提供了裁剪工具development kit。这里…...

图基本概念
图:顶点和边的集合。无向图:每条边都是无方向的有向图:每条边都是有方向的完全图:任意两个点都有一条边相连稀疏图:有很少边或弧的图稠密图:有较多边或弧的图网:边/弧带权的图邻接:有…...
机器学习基础
一、基本概念 1 学习的概念 1975年图灵奖获得者、1978年诺贝尔经济学奖获得者、著名学者赫伯特.西蒙 (Herbert Simon) 曾下过一个定义: 如果一个系统,能够通过执行某个过程,就此改进了它的性能,那么这个过程就是学习.由此可看出,…...

FreeRTOS-Tickless低功耗模式 | FreeRTOS十四
目录 说明: 一、低功耗模式简介 1.1、STM32低功耗模式 二、Tickless模式 2.1、Tickless模式如何功耗 2.2、Tickless模式设计思想 2.3、为了降低功耗,又不影响系统运行,怎么能做到呢? 三、Tickless模式修改配置 3.1、配置…...
实现了统一消息中心的微服务基础框架 JVS,快点赞收藏
一、开源项目简介基于JVS(基于spring cloud封装)的基础开源框架,实现了基于多对多租户能力的管理系统。二、基础框架实现功能支持数据管理支持分布式定时任务支持分布式日志采集支持系统监控支持动态配置中心支持模板消息支持链路跟踪支持邮件…...

VMware 安装 OpenWrt 旁路由并配置 PassWall
1、准备 OpenWrt 镜像包 我已经转好了 vmdk 格式的,更多的可以去恩山论坛下载 OpenWrtvmdk格式-虚拟化文档类资源-CSDN下载 也可以在这个平台在线定制 OpenWrt固件下载与在线定制编译 2、网络选择 NAT 模式 3、创建虚拟机,选择自定义方式 4、一直下…...

R语言GD包地理探测器分析时报错、得不到结果等情况的解决方案
本文介绍在利用R语言的GD包,实现自变量最优离散化方法选取与执行、地理探测器(Geodetector)操作时,出现各类报错信息、长时间得不到结果等情况的解决方案。 在之前的文章R语言GD包基于栅格图像实现地理探测器与连续参数的自动离散…...

嵌入式开发:你需要知道的5种简单
传达嵌入式软件体系结构设计意图通常伴随着基于嵌入式开发人员经验的假设。你可以从资源受限的基于微控制器的系统的角度来看架构设计。如何设计架构将取决于系统的嵌入式软件分类。有许多不同的方法可以对嵌入式软件进行分类。我发现有五种简单的嵌入式软件分类可以帮助我调整…...
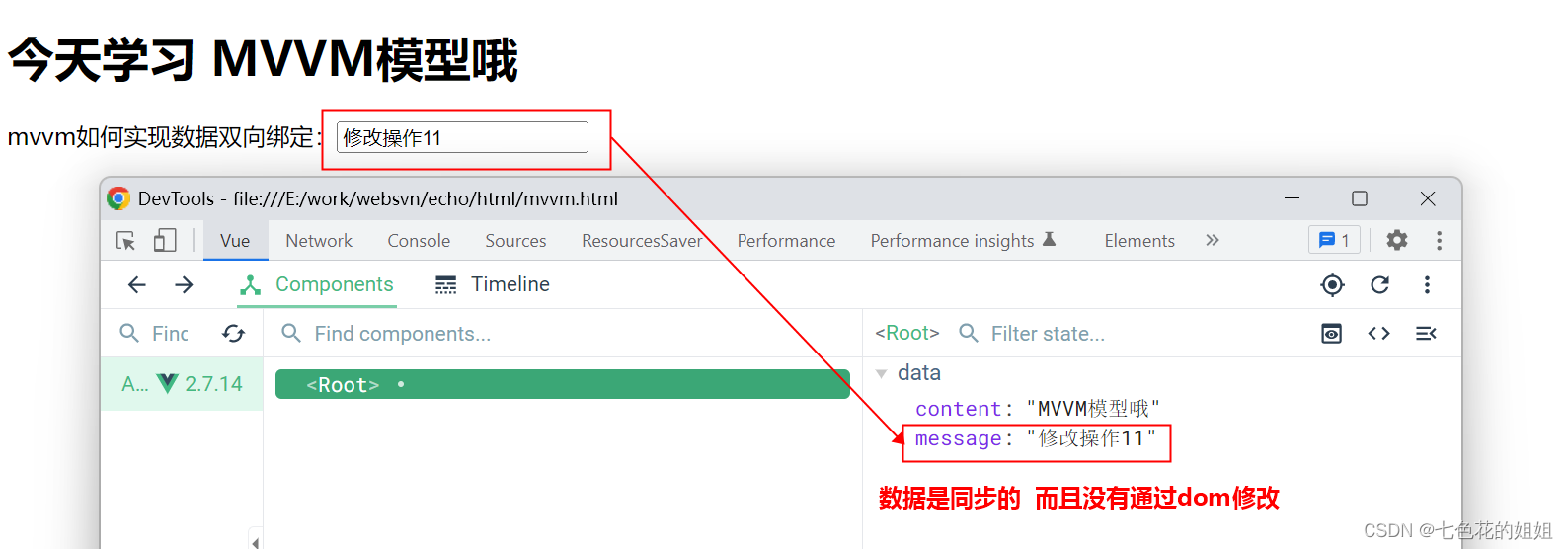
MVC与MVVM
MVC与MVVM举例说明MVCMVVM两者比较MVC <!DOCTYPE html> <html><head><meta charset"utf-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><title>mvc案例</title><link rel"styleshe…...
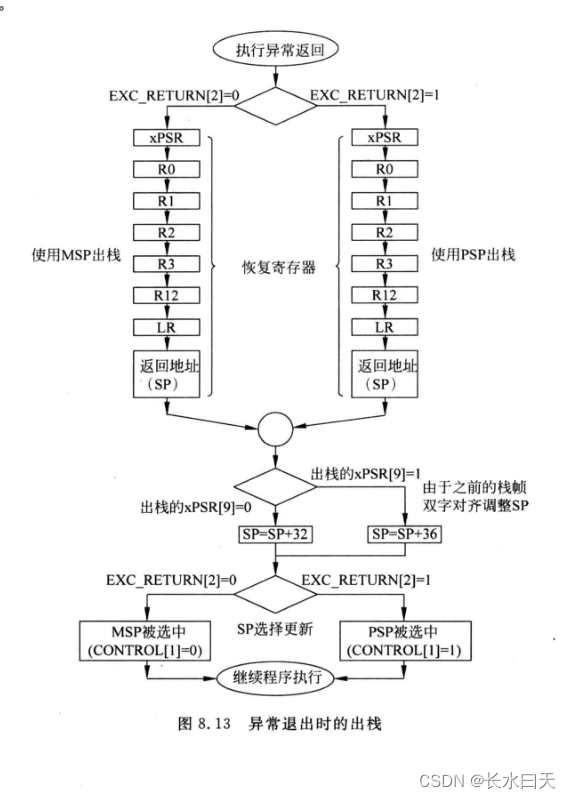
Cortex-M0异常和中断
目录1.概念2.异常类型3.异常优先级定义4.向量表5.异常流程概述接受异常请求压栈和出栈异常返回指令末尾连锁延迟到达6.EXC_RETURN7.异常入口流程的细节压栈取出向量并更新PC寄存器更新8.异常退出流程的细节1.概念 异常是能够引起程序流偏离正常流程的事件,当异常发…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
