用类比方式学习编程中函数递归(个人理解仅供参考)(内含汉诺塔问题的求解)
目录
1.前言
2.递归的数学模型
3.相关的c语法
4.将递归的数学模型写成编程语言
5.利用类比方法将实际问题的代码写成函数递归的形式
例1:
例2:
6.汉诺塔问题的求解
1.前言
本人在学习函数递归编程方法的过程中,发现用类比的方式学习递归法可帮助我们在各种编程问题中将函数递归法运用于代码设计中。
在我看来,函数递归最底层的思维模型是:数学中的数列的递推公式(数列的递推公式是研究数列性质和求通项公式的核心,将递推迭代思维模型应用于代码设计中,就产生了函数递归).
2.递归的数学模型
现在我们任意给出的一个数列 {An} 的首项和它的递推公式:
A1 == 1, An == 2*A(n-1) + 1 (n>1)在数学中求解该数列的通项公式的方法有很多种,其中有一种叫做迭代法:(迭代法可以用于求解各种递推公式为一阶递推式的数列的通项)
所谓迭代法就是将递推公式中的项按照递推公式本身逐项展开(即从An开始一直逐项递值展开到A1,然后通过计算返回出结果)
接下来我们用迭代法来试求{An}的通项公式: (n>1)
An=2*A(n-1) + 1 = 2*(2*A(n-2) +1) +1 = 2*(2*(2*A(n-3)+1)+1) +1=................................以这种方式一直展开到A1再通过归纳整理便可以得出An的通项公式.
3.相关的c语法
我们知道,计算机最擅长做的事情就是重复大量地进行同一形式的计算。然而在迭代法中,我们从An开始按照 同一个递推公式 将其逐项展开直到A1这种算法显然十分符合计算机的思维模式.在C语言中我们允许函数嵌套自身即:
int func(int n) {func(n); return 0; }
调用函数的时候 函数本身在返回输出之前会先调用自身并且这样的过程会不断重复进行
为了能够最终让函数返回输出,我们要对函数向内递值进行条件约束 并且每次向内传递的值都要逼近约束条件比如:
int func(int n) {if(n>=1){ func(n-1);}else{return0;} }这样的话函数就会逐层向内递值n次后再逐层返回输出.
4.将递归的数学模型写成编程语言
现在我们想让计算机帮我们求数列{An}的任意一项的值.要求设计一个函数int func(int)输入正整数n作为形参,函数便返回An的值.
思路引导:{An}的递推公式 An= 2*A(n-1) + 1
如果递推公式中An相当于代码中的 func(n),那么A(n-1)则相当于代码中的func(n-1)
结合迭代法求通项的思路和相关C语法便可写出如下代码
int func(n)
{if(n>1) //递推公式的成立条件{return 2*func(n-1)+1; //数列的递推公式} else{return 1 ; // 数列首项为以1}
}计算机在执行这段代码时就会自动帮助我们完成迭代的过程.(该过程中函数减值向内递值直到最后一次向内递入整数1【“递”过程】,再从最内层函数开始逐层向外返回数值【“归”过程】并最终得到结果)(递推公式决定函数递值的方式和函数结构,首项决定归值节点)
进一步思考可以得知,任意给定一个数列,只要我们知道其首项和递推公式,我们就可以写出与上面代码形式相同的代码用于求任意项的数值.
5.利用类比方法将实际问题的代码写成函数递归的形式
例1:
问题:设计一个函数代替库函数strlen() ,用于求字符串长度,形参是char*类型 返回值是int类型.
我们自定义函数取名叫做restrlen()
假设我们要求字符串“bite”的长度. 创建字符串数组char arr[]="bite".
先抽象出一个数列的某一项 restrlen("bite")
我们可以得到递推关系 restrlen("bite") = restrlen("ite") + 1
鉴于题目要求,求“bite”长度时我们只能将arr即字母b的地址传入函数中
那么restrlen("bite")就相当于restrlen(arr),类似地,restrlen("ite")就相当于restrlen(arr+1)
于是递推关系就变成了 restrlen(arr)=restrlen(arr+1) +1
该问题中首项是restrlen(arr+x) = 0 , x为某一整数 并且满足*(arr+x)="\0" 于是我们便有了如下代码:
int restrlen(char* x) {if(*(x+1)!=0) //类似于递推公式成立条件{return restrlen(x+1) +1; //类似于数列递推公式}else{return 0; //类似于首项} }
例2:
问题:设计一个函数当输入一个整数时,函数会依次输出打印出该整数每一个十进制位上的数字如:输入123 打印1 2 3
我们给函数取名叫做 prt 以输入123为例子
要先打印出1 那么1肯定在最内层函数完成输出(归值从内而外)
先抽象出一个数列的项prt(123) 其前一项可以抽象为prt(12)
那么我们便可以抽象出其递推公式 prt(123)= prt(12) + "printf("%d",123 %10)
如果数列的中n相当于“123”,那么n-1则相当于“123/10”
当输入值整除10等于0时就得到“首项” (类比意义上) “首项”的值为0
由于函数输出方式为打印输出所以无需返回值(注意要先向内层递值再打印输出)
void Print(int n) {if(n/10!=0){Print(n/10);printf("%d",n%10);} }
6.汉诺塔问题的求解

先从数学角度对汉诺塔问题进行分析:现在设 将A柱上n个圆盘借助B柱移动到C柱 需要移动圆盘的总次数为Xn.
显然我们可以得到数列{Xn} ,其中n>=1 接下来我们来研究该数列的递推公式 即尝试研究Xn与Xn-1的关系
从特殊到一般的方法对问题进行分析 我们可以分析出如下规律;
- 为了将A柱上n个圆盘借助B柱移动到C柱,我们必须经历这样一个步骤:将A柱上最大的圆盘移动要C柱上.
- 在完成1.分析中所述的步骤之前,A柱上必须只剩一个最大的圆盘,C柱必须的空的,此时B柱上则有n-1个圆盘
- 因此我们必须在游戏开始后先完成另外一个步骤:将A柱上n-1个圆盘借助C柱移动到B柱上.
- 我们称分析3.中所述步骤为:第一步骤(我们无需理会该步骤具体是如何进行的)称分析1.中所述步骤为:第二步骤
- 很显然若Xn代表n个圆盘的汉诺塔问题中需要移动圆盘的总次数,那么第一步骤需要移动圆盘的总次数为Xn-1次
- 同时,第二步骤需要移动圆盘的总次数为1次
- 在完成了第一步骤和第二步骤后我们便可以无视C柱上那个最大的圆盘接着分析下一步
- 接下来,我们只需 将B上的n-1个圆盘借助A柱移动到C柱 我们称这一步为 第三步骤(我们同样无需理会该步骤具体是如何进行的)
- 显然完成第三步骤所需移动圆盘的总次数同样为Xn-1 次
通过上述分析我们可以得到结论:为了解决n(n>1)个圆盘的汉诺塔问题我们需要经历如下三个步骤(设总移动圆盘的次数为Xn) (这里A为起始柱,B为过渡柱,C为目标柱)
第一步骤:将A柱上n - 1个圆盘借助C柱移动到B柱上(移动Xn-1次)(这里A为起始柱,C为过渡柱,B为目标柱)
第二步骤:将A柱上剩下的那个最大的圆盘移动要C柱上(移动1次)
第三步骤:将B上的n - 1个圆盘借助A柱移动到C柱(移动Xn-1次)(这里B为起始柱,A为过渡柱,C为目标柱)
即得到数列的递推公式(n>1):Xn = ( Xn-1 ) + (1) + (Xn-1)/*移动圆盘的总次数*/ /*第一步骤*/ /*第二步骤*/ /*第三步骤*/当n==1时显然我们只需执行一次第二步骤 即X1==1
利用上面的数学结论我们来尝试解决汉诺塔的c语言编程问题
编程的要求是:设计一个函数 输入形参n作为初始圆盘总数 函数(比如输入n==3时)以如下的形式打印输出(以这种形式告诉用户解决n个圆盘的汉诺塔问题的每个具体的圆盘移动步骤)A-->C A-->BC-->BA-->CB-->AB-->CA-->B
根据数学递推公式的分析我们可以初步得出:汉诺塔函数中我们有两个减值向内层函数递值的步骤(“递”步骤) 中间还有一个移动单个圆盘的步骤
很显然中间那个移动单个圆盘的步骤可以作为我们函数递归的返回输出节点(即从最内层函数开始向外层函数返回输出的“归”步骤)
于是我们可以得到如下函数递归框架:void Hanoi(int n) //总过程:将A柱上n个圆盘借助B柱移动到C柱{Hanoi(n - 1); /*第一步骤(函数向内递值 即“递”的步骤)*/printf() ; /*第二步骤(该步骤具体实行打印输出 即"归"的步骤)*/Hanoi(n - 1); /*第三步骤(函数再一次向内递值)*/}
以上便是根据汉诺塔问题数学分析得出的基本递归框架
然而为了将 《最外层函数的“将A柱上n个圆盘借助B柱移动到C柱”过程》以及《第一个内层函数的“将A柱上n - 1个圆盘借助C柱移动到B柱上”过程》以及《第二个内层函数的“将B上的n - 1个圆盘借助A柱移动到C柱”过程》 三者区分开来
我们必须引入三个字符形参代表A B C三个柱子 并且通过这三个字符形参在函数小括号()中的排列顺序的区别来区分前句分析的三个过程
于是我们可以进一步填充函数递归框架 并给出函数向内递值的限制条件完成代码设计int count = 0; void Hanoii(char a, char b, char c, int n) {if (n >= 1){ Hanoii(a, c, b, n - 1); count++;printf("%d. %c-->%c\n", count, a, c); Hanoii(b, a, c, n - 1); } } int main() {char x = 'A';char y = 'B';char z = 'C';int k = 0;scanf("%d", &k);Hanoii(x, y, z, k);return 0; }

相关文章:

用类比方式学习编程中函数递归(个人理解仅供参考)(内含汉诺塔问题的求解)
目录 1.前言 2.递归的数学模型 3.相关的c语法 4.将递归的数学模型写成编程语言 5.利用类比方法将实际问题的代码写成函数递归的形式 例1: 例2: 6.汉诺塔问题的求解 1.前言 本人在学习函数递归编程方法的过程中,发现用类比的方式学习递归法可帮助我们在各种编…...

【云原生之Docker实战】使用Docker部署Taskover开源个人任务管理工具
【云原生之Docker实战】使用Docker部署Taskover 开源个人任务管理工具 一、Taskover介绍1.Taskover 简介2.Taskover功能二、检查本地docker环境1.检查系统版本2.检查docker版本3.检查docker状态4.检查docker compose版本三、下载Taskover镜像四、部署Taskover应用1.创建安装目录…...

5、SQL编程开发与注意事项
1.1 导入数据 导入测试库: 文档地址: https://dev.mysql.com/doc/employee/en/sakila-structure.html下载地址: https://github.com/datacharmer/test_db导入测试库: mysql -uroot -p -S < employees.sql 1.2 库操作 增:create database test character set utf8;删:d…...
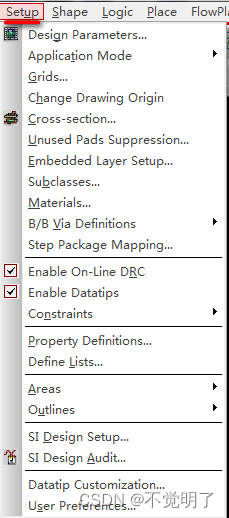
Allegro如何通过视图显示区分动态和静态铜皮操作指导
Allegro如何通过视图显示区分动态和静态铜皮操作指导 用Allegro做PCB设计的时候,通常动态和静态铜皮是无法通过视图显示区分的,只能通过show element查看得知,如下图 左边铜皮是动态铜皮,右边是静态铜皮 但Allegro可以通过一些设置让动静态铜皮以不同效果显示出来 具体操…...

测试开发之Django实战示例 第十一章 渲染和缓存课程内容
第十一章 渲染和缓存课程内容在上一章中,使用了模型继承和通用关系建立弹性的课程、章节和内容的关联数据模型,并且建立了一个CMS系统,在其中使用了CBV,表单集和AJAX管理课程内容。在这一章将要做的事情是:创建公开对外…...
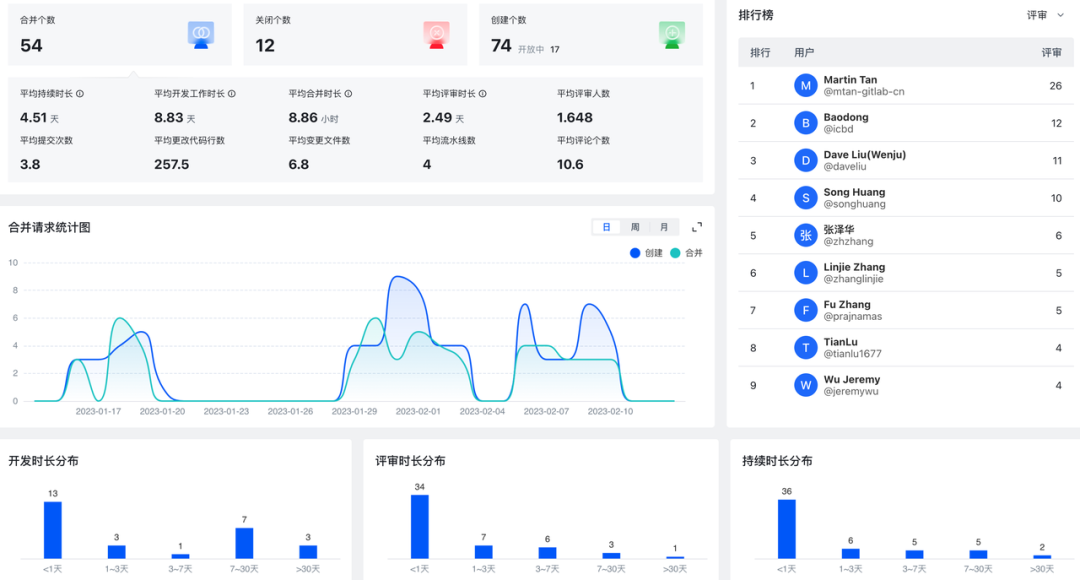
90%企业在探索的敏捷开发怎么做?极狐GitLab总结了这些逻辑与流程
本文来自: 彭亮 极狐(GitLab) 高级产品经理 毛超 极狐(GitLab) 研发工程师 极狐(GitLab) 市场部内容团队 “敏捷” 是指能够驾驭变化,保持组织竞争优势的一种能力。自 2001 年《敏捷宣言》以来,敏捷及敏捷开发理念逐渐席卷全球。中国信通院《…...

LeetCode-257. 二叉树的所有路径
目录题目分析递归法题目来源 257. 二叉树的所有路径 题目分析 前序遍历以及回溯的过程如图: 递归法 1.递归函数参数以及返回值 要传入根节点,记录每一条路径的path,和存放结果集的result,这里递归不需要返回值,代…...

测试用例该怎么设计?—— 日常加更篇(下)
😏作者简介:博主是一位测试管理者,同时也是一名对外企业兼职讲师。 📡主页地址:【Austin_zhai】 🙆目的与景愿:旨在于能帮助更多的测试行业人员提升软硬技能,分享行业相关最新信息。…...

Java基础:接口
1.接口的概念 当不是所有子类, 而是多个子类都包含一个方法时, 为了代码书写规范性, 可以用自定义的接口来统一该方法的书写规范. 所以接口可以看作是一种书写规则. 接口是对行为的抽象 抽象类一般是书写在父类当中, 接口是单独书写的, 不是一种类 2.接口的定义和使用 3.接口…...

vuex基础入门:uniapp实现用户登录授权实战
1.背景 vuex是数据共享方案之一,本文以微信小程序登录授权为例介绍一下vuex常用属性state、getters、mutations、actions. 2.基于uniapp实现微信小程序登录授权流程 1.凡是需要用户登录授权信息的页面创建时created方法中需要判断用户是否登录,需要使用本地缓存的token调用服务…...

Windows系统从权限维持角度进行应急响应
一、基本介绍 红队攻击者在对目标进行渗透利用后通常都会进行权限维持,以达到持续利用的目的。而作为防守方进行应急响应时,应该如何与技术高超(jiaohuajianzha)的攻击者斗智斗勇呢?或许可以通过本文可以找到答案。以…...

什么是DNS解析?如何提升DNS解析安全?
DNS解析是保障网站正常运行的一项重要服务,DNS解析出现故障,就会导致网站无法被访问或者被劫持到其他的站点,对业务正常开展造成很大影响,因此网站管理人员要高度关注DNS解析的安全,才能确保网站的正常运转,…...

电路学习笔记
电源部分 2s锂电池 6.4v-8.4v INA180A2IDBVR 电流检测放大器 OUT ADC1_CH0 to ESP32 可能功能:电源电流监测 稳压/电压监测 OUT ADC1_CH1 to ESP32 降压至2.046v-2.686v并通过电容保持稳定 可能功能:降压模块,电压监测 LDO ASM1117-3.3 低压差线性…...

C# 数据结构
目录 一、介绍 二、数组 三、List(列表) 四、Dictionary(字典) 五、Queue(队列) 六、Stack(栈) 七、Hashtable(哈希表) 结束 一、介绍 数据结构是计…...

powerjob的worker启动,研究完了这块代码之后我发现了,代码就是现实中我们码农的真实写照
这是一篇让你受益匪浅的文章,代码即使人生。 worker启动比server启动要复杂一些,毕竟worker是要实际干活的,工欲善其事必先利其器,所以需要准备的工具还是不能少的,server对于powerjob来说,只是一个调度用的…...
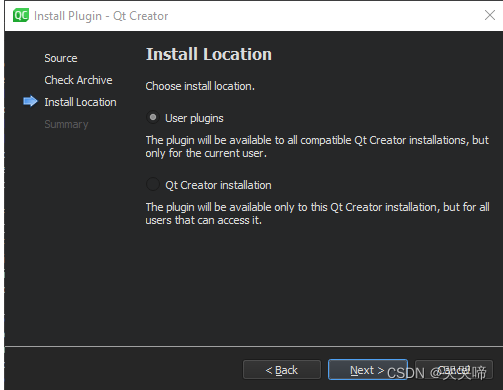
配置Qt Creator
前言 为了使Qt Creator更像您最喜欢的代码编辑器或IDE,您可以更改键盘快捷键、配色方案、通用高亮显示、代码片段和版本控制系统的设置。 检查生成和运行设置 Qt Creator是一个集成开发环境(IDE),可以用来开发Qt应用程序。虽然您可以使用Qt Installer…...
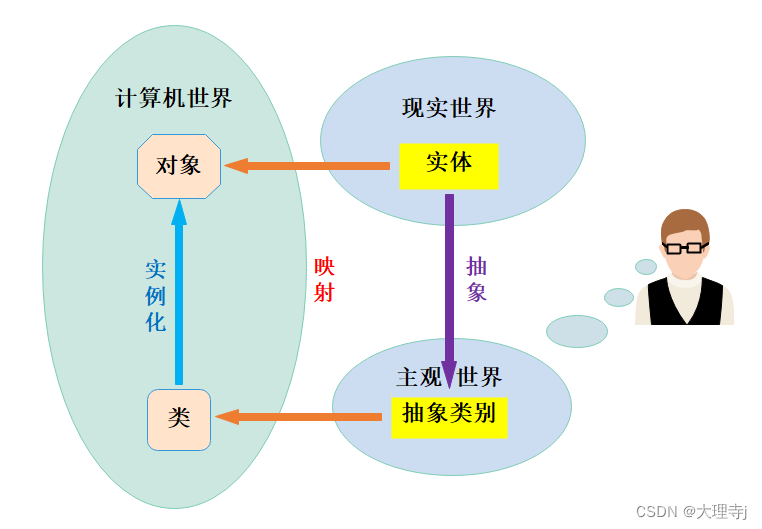
C++-类和对象(下)
C-类和对象(下)一,const成员函数二,再谈构造函数1,初始化列表2,explicit关键字三,static成员四,友元(friend)1,全局函数做友元2,类做友…...

什么是仓库管理?
仓库管理包括仓库日常运营所触及的准绳和流程。从较高的层次上讲,这包括接纳和组织仓库空间、布置劳动力、管理库存和完成订单。放大来看,你会发现有效的仓库管理触及到优化和集成这些过程中的每一个,以确保仓库操作的一切方面协同工作&#…...
对话系统学习概述(仅够参考)
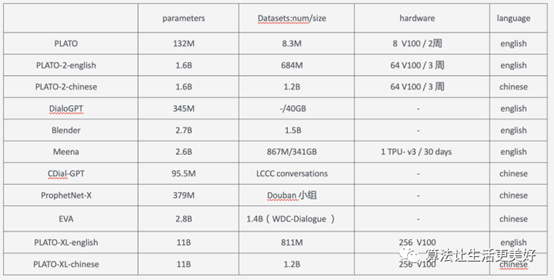
对话系统(仅够参考) 目录对话系统(仅够参考)背景类人对话系统的关键特征1、知识运用2、个性体现3、情感识别与表达数据集评价方式评价的一些指标训练模型需要的资源任务型对话系统预训练最新研究进展参考文献背景 对话系统一般包括…...

免费CRM客户管理系统真的存在吗?不仅有,还有5个!
免费CRM客户管理系统真的存在吗?当然有! 说到CRM客户管理系统,相信很多企业并不陌生,是因为CRM客户管理系统已经成为大多数企业最不可或缺的工具。但是对于很多小微企业和个人用户来说,购买和实施CRM的成本仍然难以承…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
